利用空間向量基本定理通解高考數學立體幾何解答題

■浙江省杭州市余杭區教育局教研室 (特級教師)

高考中的立體幾何解答題一般難度不大,屬于中檔題,但是,得分往往也不理想。解這類問題一般會考慮兩種方法：綜合法、空間直角坐標法(簡稱坐標法)。綜合法計算量較少,空間想象能力要求高,有些需要添加輔助線,考生無絕對把握;坐標法降低了空間想象能力的要求,但在沒有“墻角”的情況下,也會讓一部分同學發怵,不能順利建系便束手無策。

實際上,解決立體幾何解答題還有一種往往被大家忽略的基本方法：利用空間向量基本定理求解(簡稱基底法)。

下面以近幾年浙江高考數學立體幾何解答題為例,對利用基底法解幾類常見問題的方法、步驟演示說明。順帶指出,本文不具體比較三種方法的優劣,只是體現利用空間向量基本定理解決問題的通法意義。

1.線線、線面垂直,直線與平面所成角問題

例1(2018 年浙江高考數學第19題)如圖1,已知多面體ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2。

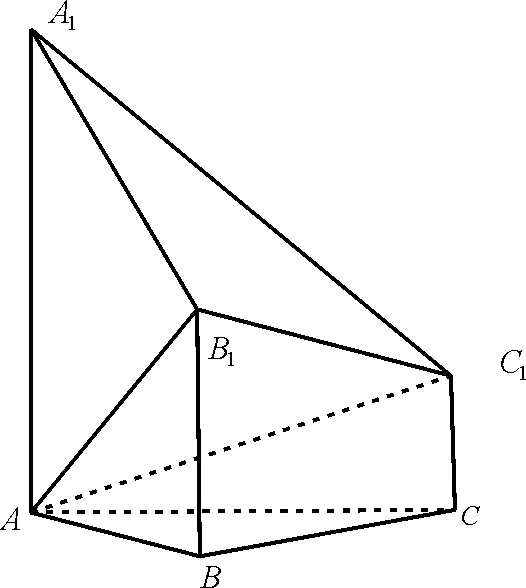
圖1

(1)證明：AB1⊥平面A1B1C1;

(2)求直線AC1與平面ABB1所成的角的正弦值。

分析：根據已經條件,BA,BC,BB1長度已知,且兩兩夾角已知,可以選取為基底,然后用基底表示所需的向量、平面法向量。線面垂直可以考慮求向量的數量積,線面所成角的正弦值先求出直線所在向量與平面法向量所成角的余弦值。

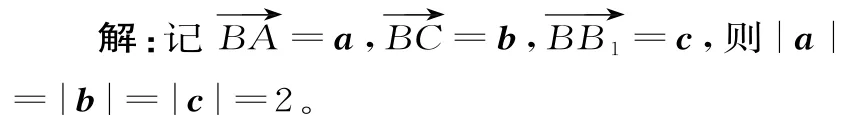
于是得,直線AC1與平面ABB1所成的角的正弦值為

反思：基底法降低了空間想象方面的要求,解題具有明顯的程序性,可以按部就班處理。①確定基底(比如：從同一個點出發,三個長度、兩兩夾角已知或易求的向量);②用基底表示所需的向量;③待定系數法確定所需平面法向量(如設為n=xa+yb+zc,這里設為n=a+xb+yc是為簡化計算,有些情況下不能簡化,參見下面例3);④根據待求、待證,設計合理的向量運算(線線垂直轉化為求涉及向量的向量積,線線角、線面角轉化為求向量所成角的余弦值等),并準確得到結果;⑤把計算結果翻譯成立體幾何有關結論(如：利用向量求出法向量與直線所在向量所成角的余弦值的絕對值,待求的是直線與平面所成角的大小(或某種三角函數值),注意兩者之間的區別與聯系)。

2.線線、線面平行問題

例2(2017 年浙江高考數學第19題)如圖2,已知四棱錐P-ABCD,△PAD是以AD為斜邊的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E為PD的中點。

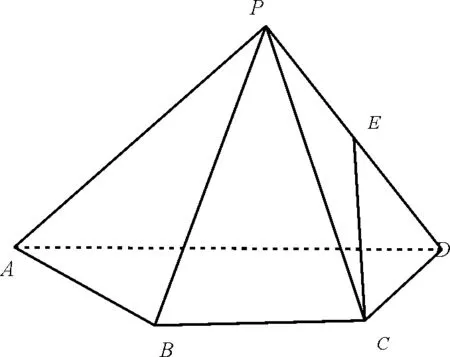
圖2

(1)證明：CE∥平面PAB;

(2)求直線CE與平面PBC所成角的正弦值。

分析：根據題設,PA,PD,DC長度已知,PA⊥PD,可以選取為基底,注意相應的數量積的運算。線面平行的判定可以考慮平面向量基本定理。

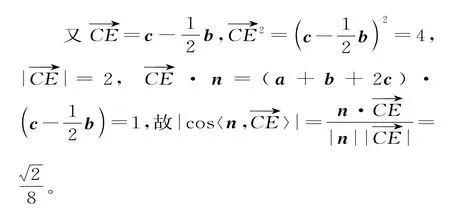
所以直線AC1與平面ABB1所成的角的正弦值為

反思：①基底的選取方式不唯一,也可以選取不是同一點出發的三個不共面向量,基底要盡量有利于便捷地表示其他向量,便于計算;②本題可以選取同一點出發的向量為基底,如通過解三角形確定向量之間的夾角;③線線平行根據向量的共線來判定,線面平行一般采用待定系數找關系,再依據平面向量基本定理判斷。

3.二面角問題

例3(2016 年浙江高考數學第19題)如圖3,在三棱臺ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3。

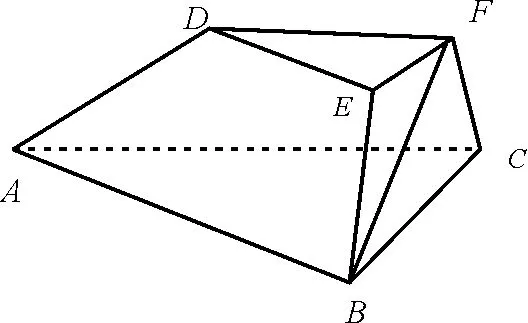
圖3

(1)求證：BF⊥平面ACFD;

(2)求二面角B-AD-F的平面角的余弦值。

分析：根據已經條件,CA,CB,CF長度已知,且兩兩夾角容易判定、求解。基底可以選取{CA,CB,CF},需要求出兩個平面的法向量,一般來說,求出一個,另一個同理即可。

解：平面BCFE⊥平面ABC,∠ACB=90°,平面BCFE∩平面ABC=BC,所以AC⊥平面BCFE,AC⊥BC,AC⊥CF,AC⊥BF。

又在三棱臺ABC-DEF中,BE=EF=FC=1,BC=2,易得

反思：(1)法向量一般形式應為n=ma+nb+kc①,前面幾個例題中取n=a+xb+yc②是出于簡化計算,本題中,若設②的形式,由出現矛盾,其原因在于法向量在基底的其中兩個向量b,c確定的平面內,處理方法一種是直接設成①的形式,再一種設成②的形式,若出現矛盾關系,再回到①;(2)理解兩個平面法向量所成的角(三角函數值)與二面角的平面角的關系,注意轉化為立體幾何結果的等價性。

從以上三個例題可以看出,基底法在解決立體幾何位置(垂直、平行、所成角)關系問題時具有通性通法意義,解題可操作性強,在理解原理的基礎上,大部分同學可以熟練運用。當然,綜合法、坐標法、基底法各有優劣,能夠根據具體問題靈活選擇方法是解題追求的理想境界。