基于垂直約束的深海拖曳系統USBL/DVL組合導航算法

王振杰，劉慧敏，楊慧良，賀凱飛，單 瑞

（1.中國石油大學（華東），青島 266580；2.青島海洋科學與技術國家實驗室 海洋礦產資源評價與探測技術功能實驗室，青島 266071；3.中國地質調查局青島海洋地質研究所，青島 266071）

深海拖曳系統（Underwater Towed System,UTS）由母船通過長纜提供動力，廣泛應用于深海科學研究以及海底調查，例如，測量海底地形測量及海底底質調查等[1]。實時高精度的動態導航定位是其進行近海底、遠距離、長時間工作的重要保障[2]。常見的深海拖曳系統導航傳感器包括光纖羅經、壓力傳感器、多普勒計程儀（Doppler Velocity Log,DVL）以及超短基線定位系統（Ultra-Short Baseline System,USBL）等，可提供運載體的姿態和方位信息、深度信息、速度信息和位置信息等。超短基線定位系統可為拖曳系統在淺水區域提供高精度位置信息，但受姿態測量精度、時延和聲速誤差的影響，其精度隨著拖曳系統與母船的距離增加而降低。拖曳體下潛至5000 m左右的深水中時，超短基線定位系統的定位精度甚至不足10 m[2]。拖曳系統貼近海底進行工作時，多普勒計程儀可提供載體相對海底的速度信息，結合載體姿態傳感器以航跡推算的方式求解地理坐標，因測速誤差的影響，其位置誤差隨時間累積。拖曳系統在深海的工作環境復雜，單一的導航系統通常存在各種各樣的局限性，需要多種傳感器的導航信息密切配合。

采用RDOA（Range Difference of Arrival）模式定位的USBL定位誤差隨斜距增長而增加，在深海中USBL定位系統的測距精度要明顯優于其定位精度[3]。校準后的壓力傳感器的測深精度為米級，因此可利用拖曳系統上的壓力傳感器測得的深度信息、USBL換能器實時吃水信息與超短基線測距信息進行耦合，以提高超短基線定位系統的水平定位精度。

為合理利用多源導航信息，常采用線性的卡爾曼濾波算法進行數據融合；對于非線性模型，則多采用基于線性近似的擴展卡爾曼濾波算法和基于確定性采樣的無跡卡爾曼濾波算法[4]。本文基于自適應抗差濾波算法思想[5]和深度約束信息設計了一種適于深海拖體長時間、長距離觀測的自適應抗差無跡卡爾曼濾波算法。該濾波算法可以利用深度約束信息提高濾波精度，同時通過新息向量判別定位數據中的粗差觀測，提高了濾波算法的魯棒性。

1 深海拖曳定位系統的深度傳感器信息獲取

如圖1 所示，深海拖曳系統的導航傳感器包括安裝在母船的 GPS及姿態傳感器和安裝在拖體上的超短基線定位系統、深度計、多普勒計程儀、光纖羅經等。GPS天線可以獲得母船的絕對坐標，并通過姿態傳感器得到USBL換能器基陣坐標。換能器基陣使用多個（3個以上）測量單元，測量信標聲信號到達各單元的時間差及聲信號延遲，得到信標相對于換能器的相對坐標。

壓力傳感器測量拖曳系統到瞬時平均海面的垂直距離，由于其性能穩定且精度較高，可視為同GPS一樣穩定可靠的導航信息源。如果拖曳系統接近海底，多普勒計程儀可以測量拖體相對海底的速度信息，結合姿態信息可得到其航跡推算位置。多普勒測速信息以及壓力傳感器測得的深度信息都可以有效地提高深海超短基線的定位精度。下面將詳細介紹這幾種導航數據的組合導航原理。

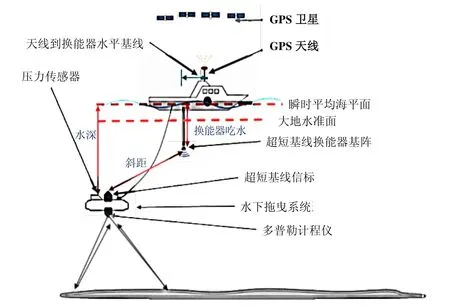
圖1 基于USBL/DVL/GPS的拖曳導航系統示意圖Fig.1 Deployment of USBL and geometrical relationship with GPS and DVL

1.1 無波浪影響的深度信息獲取

由于海面波浪、潮汐及其他因素的影響，實時海平面在不斷的變化。在淺水區，可假設由壓力傳感器測量得到的到海平面的垂直距離Di為[6]：

定義換能器瞬時高程為Hi可由 GPS天線求得，瞬時海面高程為Zi，且有Zi=Hi+Hd，其中，應答器的動態吃水改正為Hd。通常，潮汐的周期長達數小時，短時間內潮汐對動態吃水的高程影響可以暫不考慮。波浪的周期僅有數秒至幾分鐘，因而波浪對USBL換能器造成的動態吃水影響可以通過取多個歷元的平均值或其他平滑算法盡量消除，此時的瞬時海面高程可表示為：

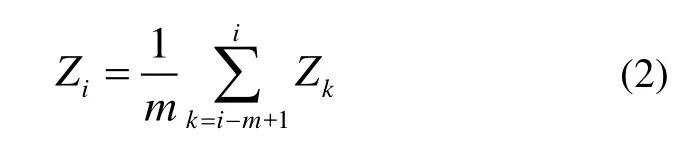
如圖2(a) 所示，采用2000s的船測GPS數據，并通過姿態改正和吃水改正后得到瞬時海平面的高程。利用所有的觀測數據并使用經驗模態分解（Empirical Mode Decomposition,EMD）去除高頻分量，并作為離線解算方案。與式(2)計算的瞬時海面高程對比，二者差距僅為數厘米。由圖2(b)所知，深海中載體溫鹽深（Conductivity Temperature Depth,CTD）傳感器測量得到的深度值比較平滑。此外 DVL測量的速度值在垂向上的積分在短時間內有較好的結果，但隨著時間的累積容易發散。壓力傳感器可得到平滑的瞬時平均海平面，校準后精度達數厘米；而USBL換能器到瞬時平均海平面的距離可以通過式(2)粗略估計，二者之間的差值即為本文討論的垂直約束信息。

圖2 (a) 換能器到大地水準面的距離Fig.2 (a) Vertical distance from USBL transducer to the mean sea level

圖2 (b) CTD測得及DVL垂向積分的深度Fig.2 (b) Depth from CTD and DVL

1.2 深度約束提高USBL定位精度的幾何解釋

超短基線定位精度多與斜距有關，USBL的測距誤差精度優于米級，測角精度不夠往往是水平定位誤差的主因。假設其精度為 1‰～5‰，斜距為 6000 m時，USBL的定位精度為6～30 m。可結合垂直深度約束信息和高精度斜距信息給出可靠的水平約束。本節給出了二者耦合的幾何原理。

為研究垂直約束對水平方向精度的影響，先不考慮測距誤差對垂直約束的影響。如圖3所示，在X-Z平面中，點A為換能器基陣的位置，點C和D分別為測量和真實信標位置，則由測角誤差dθ引起的定位誤差在X-Z平面的投影為CD，深海中其值可達數十米。此時USBL得到的高程誤差值為dh，深度約束改正即將C投影到E點。易得在X-Z方向上提高的精度為CD減DE。

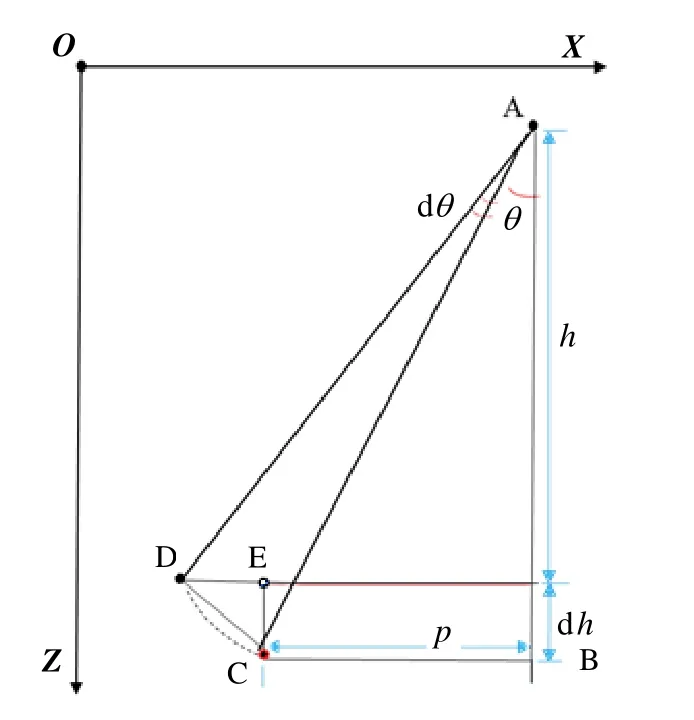
圖3 垂直約束條件下超短基線信標與基陣的幾何在垂直面的關系Fig.3 Geometrical relationship between USBL and target in X-Z

母船沿直線航行時，水下拖體通常在水平方向上近似沿直線運動。拖體在拖體坐標系和導航坐標系下的速度可表示為

其中，[X,Y]和[εx,εy]分別是載體坐標系下的位置和誤差。因此在水平直線航行的條件下，根據航向信息，通過式(3)可轉化成載體坐標系下的坐標，通過選取一段時間的觀測值，對拖體的垂直運動方向上的位置進行平滑，可明顯提高其定位精度。上述方法更可作為無DVL觀測信息時的重要補充。

2 自適應抗差無跡卡爾曼濾波

由于聲信號在海水中的不穩定性，USBL和DVL觀測值中往往存在大量的粗差觀測。本節使用自適應抗差無跡卡爾曼濾波（Adaptive Robust Unscented Kalman Filtering,ARUKF）對USBL、DVL和深度信息進行融合。采用抗差IGG-3方案對粗差觀測進行判定和處理，保證濾波算法在長時間觀測下的穩定性。

2.1 狀態方程和量測方程定義

定義狀態模型參數：

其中，xn(k)、xe(k)、ψ分別為北、東方向的位置和航向角，vf(k)和vs(k)為載體坐標系下的速度。非機動情況下的狀態方程可簡化為[7]：

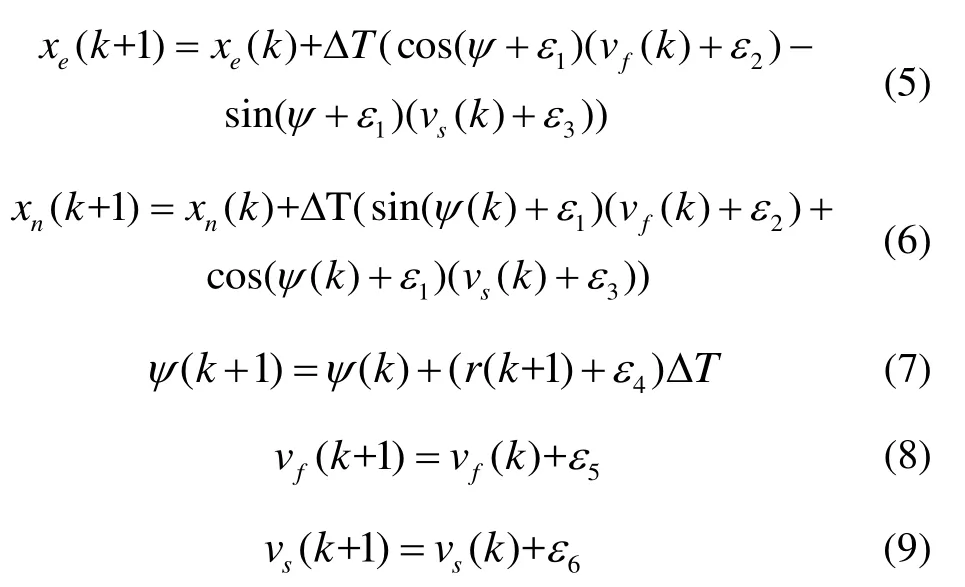
其中，ε表示過程噪聲，ΔT為采樣間隔。觀測向量定義為且

Ya(k)由 USBL在導航坐標系下的位置測量值(xusbl,n(k),xusbl,e(k))、DVL在載體坐標系下的速度測量值(vdvl,f(k),vdvl,s(k))以及航向角ψgro組成。深度約束信息可寫為：

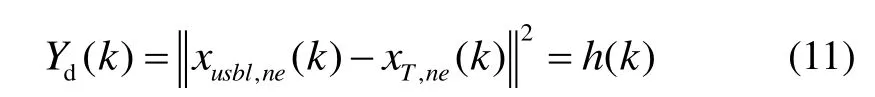
2.2 自適應抗差無跡卡爾曼濾波（ARUKF）

無跡卡爾曼濾波通過無跡變換（Unscented Transform,UT）給出的確定性采樣，得到非線性變換后變量的均值和方差信息，理論上可以達到二階以上的擴展卡爾曼濾波（EKF）精度。假設非線性方程為y=g(x)，如果已知變量x的均值和協方差矩陣Px，無跡變換過程如下[8-12]：

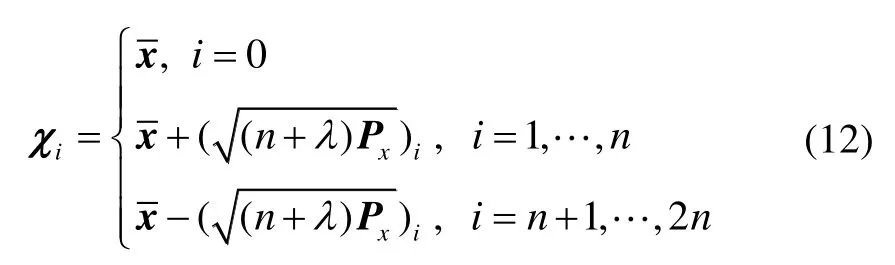
其中，χi表示采樣點，n最小必要采樣數，而λ可影響采樣點到x的距離。點γi=g(χi)(i= 1,,2n)被依次計算，要估計的g(x)的均值及協方差矩陣Py和相應的權值及可快速求出。

自適應無跡卡爾曼濾波主要分為以下四個步驟：

1）初始化（計算初始狀態及其協方差陣）

2）生成采樣點

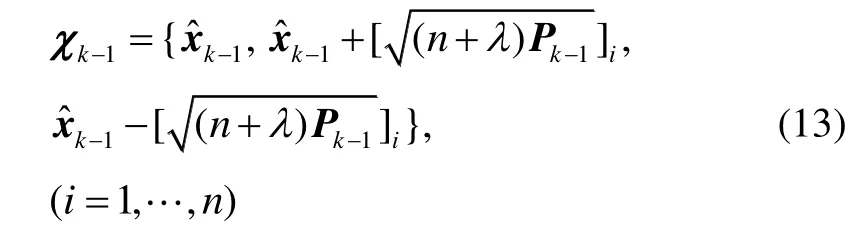
3）時間更新

4）量測更新

本文主要通過新息序列和等價權函數來消除粗差觀測值帶來的影響。通過粗差對新息序列的異常影響對粗差進行識別，并通過量測矩陣的膨脹因子處理粗差觀測值。具體過程如下：

根據式(28)，膨脹因子?k被分為正常、可能正常、異常三種情況，其中c0和c1可根據正常穩定的觀測情況下的標準化殘差數量級給出。修正后的觀測值的協方差矩陣為：

在深海中，非線性情況并不突出，但拖體上浮過程中，垂直約束方程的非線性程度會變強。而 UKF算法并不需要直接解算雅克比矩陣，能方便得到非線性方程的統計信息，在非線性較強的系統中明顯優于一階EKF濾波算法。當觀測值中存在粗差觀測值時，信息向量一般會出現異常，此時通過增大觀測噪聲矩陣使得濾波器拒絕該觀測信息，僅從狀態方程和其他觀測信息預測出該時刻的狀態信息，從而提高濾波器的容錯性。

3 實驗分析

3.1 仿真實驗

首先通過仿真實驗對基于深度約束的 ARUKF算法的定位精度和穩健性進行分析。仿真水深為5000 m，拖體以3 m/s 的常速度航行。導航傳感器測量誤差見表1。

表1 USBL/DVL/Depth/Attitude仿真參數Tab.1 Simulation parameters of USBL/DVL/Depth/attitude

表1中，R表示隨機噪聲，S表示系統偏差。USBL基陣到信標的斜距為Ra，其測量精度為Ra/5000。DVL測量拖體在載體坐標系下的速度。母船和拖曳系統按圖5的整齊的巡回模型航行。

使用30000個歷元的直線觀測值對平滑算法的性能進行測試，給出原始USBL結果、深度約束（USBL&DEPTH）的結果和MEDFILT平滑方案。MEDFILT方案是采用10個歷元數據的開窗平滑算法（MEDFILT

圖4 水下拖曳系統的軌跡示意圖Fig.4 Trajectory of underwater towed system

在本文指中值濾波方法）。MEDFILT方案首先將載體深度約束后的位置轉換成載體運動坐標系，并在垂直于運動方向上進行平滑處理。

如圖5所示，經深度約束（USBL & DEPTH）后的水平位置精度明顯優于USBL原始觀測值。為研究深度約束與拖體和母船運動狀態之間的關系，繪制了縮小10倍的二者航向角之差YAW。垂直約束后精度變化的趨勢同 YAW 的趨勢明顯相關，當存在較大定位誤差的情況時，拖體水平位置雜亂無序，但經過深度約束改正后沿船航行方向上的定位精度明顯提高，與上文分析的結論相符。因考慮到載體水平運動狀態模型，MEDFILT 方案精度較 USBL&DEPTH 算法進一步提高。仿真實驗采用平均絕對誤差（ Mean Absolute Error,MAE） 來評定算法的平均精度，其定義為：

圖5 開窗平滑算法定位誤差圖Fig.5 Positioning residuals of MEDFILT

表2給出前1000個歷元的直線運動狀態的解算結果。仿真實驗中船沿北方向上航行，深度約束算法在北方向上的深度約束效果明顯優于東方向。結合圖5和表2 可得，MEDFILT 算法通過深度約束信息和開窗平滑處理，明顯提高了直線狀態下垂直于運動方向上的定位精度，當載體運動方向垂直的速度為 0時，MEDFILT方案在東方向精度較深度約束方法提高了4 m左右。

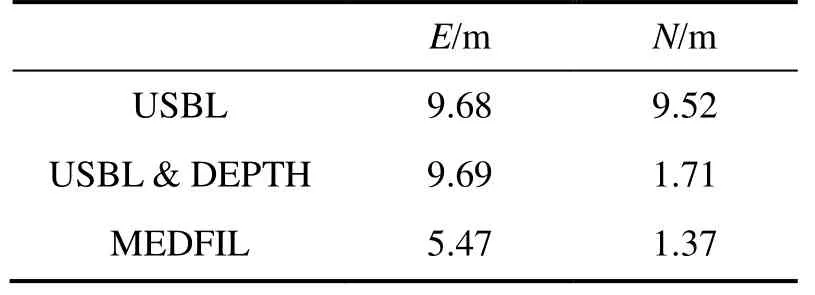
表2 直線狀態下的平均絕對誤差Tab.2 Mean absolute errors of straight line

為驗證自適應無跡抗差卡爾曼濾波算法的精度和容錯性能，本文分別設置了不含粗差和含粗差的兩種實驗，并采用標準無約束卡爾曼濾波（KF）算法作為對照。如圖6所示，不含粗差情況下，ARUKF的定位精度最高，其精度明顯優于KF濾波算法，證明了深度約束對濾波算法的提高。

圖6 不含粗差情況下的定位誤差圖Fig.6 Positioning residuals of four approaches without outliers

由表3可知，不含粗差的情況下，融合多普勒觀測的KF和ARUKF濾波都可以提高載體水平定位的精度。由于垂直約束的影響，ARUKF算法在北方向上精度較KF濾波算法提高了接近2 m。

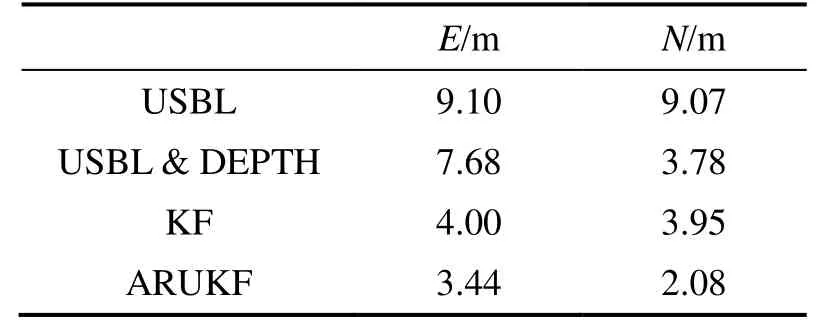
表3 不含粗差情況下的所有歷元的平均絕對誤差Tab.3 Comparison on Mean Absolute Errors of the epoch without outliers

含粗差情況時，在每100個USBL觀測值中和每150個DVL觀測中添加一個隨機的粗差（10倍觀測噪聲），通過標準無約束卡爾曼濾波（KF）和有深度約束的無跡卡爾曼濾波（UKF）作為對照來驗證算法的有效性。

如圖7所示，當USBL和DVL數據中同時含有粗差時，此時的定位精度較其他時刻要差。ARUKF濾波效果要明顯優于UKF和KF算法，證明了新算法的穩健性。

圖7 含粗差情況下的定位誤差圖Fig.7 Position residuals of the three approaches with outliers

3.2 實測實驗

圖8(a)是采集的4500 m深的USBL數據，紅綠藍三種顏色的點分別表示早、中、后三階段的位置。由圖可見，USBL觀測值的觀測精度和采樣率都比較低，并且含有一些粗差值。聲學斜距信息如圖8(b) 所示，其測距精度要明顯優于其定位精度，這是本文深度約束的基礎。

圖8 實測USBL水平位置和斜距觀測值Fig.8 Position and slant range of underwater towed vehicle by USBL

DVL傳感器測得的速度信息如圖9所示，由載體坐標系下的速度觀測值的可看出，X方向上的速度值在0值附近波動且變化幅度較小，說明拖體沿直線運動且左右擺動較小。較USBL觀測值，DVL和姿態傳感器的觀測值具有高精度和高采樣率的特點。本文采用拉格朗日插值保證采用時刻的一致。

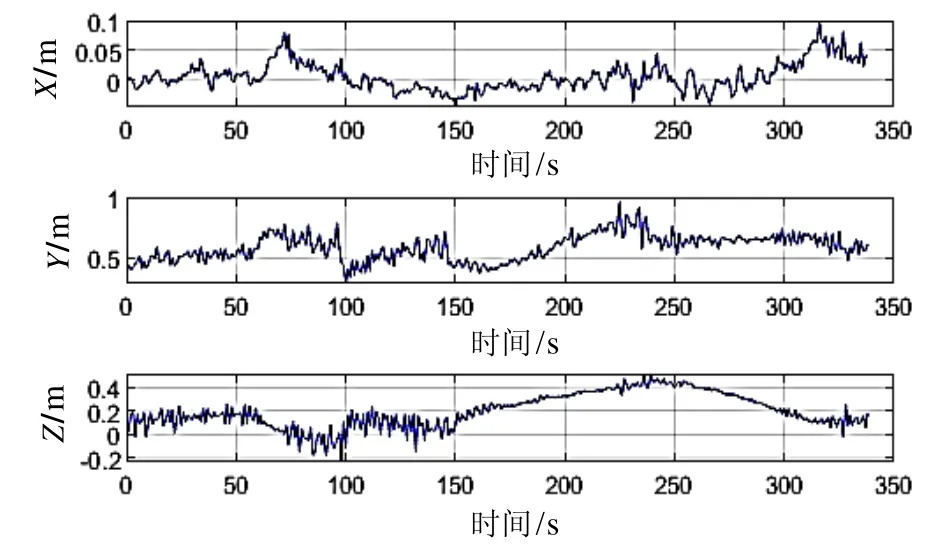
圖9 水下拖體的多普勒速度信息Fig.9 Velocity of towed vehicle measured by DVL

圖10 基于ARUKF算法的水下拖體平面位置Fig.10 Position of towed vehicle by ARUKF method

由于USBL精度較差，且粗差較多，KF算法不適合作為對照，而深度約束后的點在垂直于前進方向上的離散程度依然很大，本文使用 DVL數據進行航跡推算（DR）作為對照。如圖10所示，DR方法較USBL的位置更加平滑，因精度和采樣率不夠的問題，其在后期發散。使用深度約束的ARUKF算法定位精度在保證比較平滑的情況下，精度要高于DR算法，同時具有一定的抗差性能。

4 結 論

本文結合實測的深海拖體導航數據分析了導航傳感器的性能，采用仿真數據和實測數據驗證了新濾波算法的有效性。實驗結果表明：基于深度約束的開窗平滑算法能有效利用USBL聲學測距信息及深度約束信息提高水下拖體的定位精度；自適應無跡抗差卡爾曼濾波可以有效識別USBL數據和DVL數據存在粗差，提高算法的容錯性；該算法能有效利用深度約束信息和拖曳系統直線狀態模型，提高動態定位的精度。