基于分位數回歸方法的函數型數據phaseⅠ控制圖

李晴晴，訾雪旻

（天津職業技術師范大學理學院，天津 300222）

在工業過程生產中，質量特征不僅僅表現為一個或多個獨立變量，某些情形下則通過變量之間的某種函數關系來表示，并把此類數據稱為函數型數據。近年來，用函數型數據刻畫產品的某些特征進而分析和監控此類型的數據成為統計過程控制研究的熱點之一，文獻[1-4]介紹了統計過程控制的一些成果。目前對于函數型數據，大多采用普通最小二乘法來估計回歸系數，但研究者也越來越關心解釋變量與響應變量分布的中位數、分位數呈何種關系。為了更好地刻畫解釋變量在各個位置上對響應變量的影響，Koenker等[5]提出了分位數回歸的思想，這種方法能夠更加全面地描述響應變量條件分布的全貌，進而受到廣大研究者的關注，文獻[6-9]給出了分位數回歸在金融、教育、醫療衛生等領域的應用，但分位數回歸應用在統計過程控制中的研究則甚少。本文針對上述問題，給出分位數回歸結合控制圖的研究。假設所有的樣本函數型數據都來自一個線性模型，而備擇假設為在第m1（m1=1，2，…，m-1）個樣本之后回歸系數發生了漂移。對于上述假設提出了基于似然比檢驗（likelihood ratio test，LRT）的變點法來監控回歸系數的漂移。許多研究者在回歸建模的背景下研究了變點問題，假設在任何一個觀察之后都可能存在1 個變點，利用似然比法檢測簡單線性回歸模型中存在的變點，估計回歸模型中變點位置，以及估計變點前后的回歸系數，相關研究參見文獻[10-13]。正如Woodall[14]所討論的，第Ⅰ階段控制圖表現的好壞通常根據出現失控點（在控制線以外的點）的概率來衡量的，而這個概率通常被稱為“誤報率”。本文在給定誤報率α=0.04 的情況下，研究基于分位數回歸的變點法對函數型數據的監控表現，研究的重點是在函數型數據的基礎上構建穩健的分位數回歸估計，利用分段回歸技術結合變點法給出似然比檢驗統計量，對多個異常點給出檢驗和診斷。

1 第Ⅰ階段的線性函數型數據模型假設

1.1 單樣本模型假設

對于單變量的線性函數型數據，假設解釋變量X和響應變量Y 之間的關系用以下模型表示：在分段的簡單線性回歸模型中，假設數據集是由單個樣本（{x1，y1），（x2，y2），…，（xN，yN）}組成的。解釋變量X 與響應變量Y 之間的關系用以下k 段回歸模型表示：

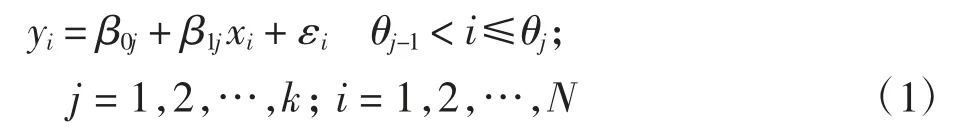
式中：β0j、β1j分別為第j 個樣本的截距項和斜率項；θj項為段與段之間的變點（通常θ0=0，θk=N）；εi為隨機誤差項。

分段線性回歸方法可用于檢測給定樣本中回歸系數的變化，估計變點的位置（θj項），并確定適當數量的變點。Hawkins[15]給出了一般分段多元回歸模型的似然公式，并給出了一種動態規劃算法，用于確定一般分段多元回歸模型的最大似然統計量。這種動態規劃算法既適用于同方差模型，也適用于異方差模型。

1.2 多樣本模型假設

在具有單個解釋變量X 和響應變量Y 的函數型數據數據集中，有m 個樣本，樣本的形式為（{Xi1，Yi1），i=1，2，…，n1}，（{Xi2，Yi2），i=1，2，…，n2}，…，（{Xim，Yim），i=1，2，…，nj}，nj＞2，j=1，2，…，m 即相當于第j個樣本中含有nj個觀測點。解釋變量X 與響應變量Y之間的關系為：

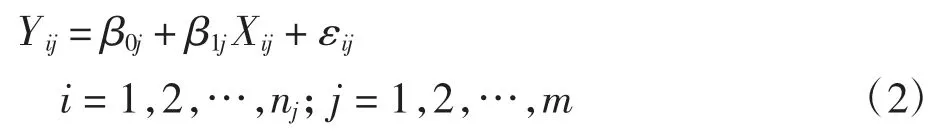
式中：εij為隨機誤差項。

在這種情況下，假設每個樣本中沒有系數變化，重點是檢測回歸系數從一個樣本到另一個樣本的變化。為了監控函數型數據數據集中回歸系數的變化，把所有的樣本合并成一個樣本容量為的樣本，并對該樣本在模型（1）的基礎上做分段回歸。正如之前假設的在每個樣本間沒有系數發生變化，因此模型（1）中的θj項受指示變量i 的限制。針對上述問題，使用文獻[16]中的LRT 檢驗回歸系數中出現的變化，并且可以遞歸地識別數據集中的多個變化。

2 估計樣本系數的回歸方法

普通的最小二乘回歸方法是線性回歸模型中最基本、最經典的方法。它刻畫了響應變量的均值，給出了響應變量和解釋變量之間的關系，但有時人們更關心不同分位數下響應變量和解釋變量的關系。相比較普通的最小二乘法，分位數回歸能夠更加全面地描述響應變量條件分布的全貌，也可以分析響應變量的中位數以及其他分位數如何被解釋變量影響。

前文給出單樣本和多樣本的回歸模型，對于單樣本模型直接對其分段，用分位數回歸的方法估計其回歸系數，而對于多樣本的模型將其合并成一個樣本容量為N 的樣本對其進行分段，方法同上。正如之前假設的線性模型，為了便于計算和表達，無論是單樣本還是多樣本數據集都將其轉化為以下形式求其回歸系數：

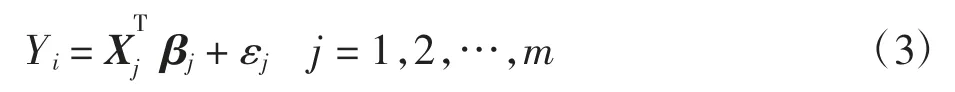
設隨機變量的分布函數為F（y）=P（Y≤y），對于任意的0 ＜τ ＜1 有F-1（τ）=inf{y：F（y）≥τ}，稱τ 為y的分位數。對于回歸而言，就是使函數型數據值與真值之間距離最短，隨機變量Y=（y1，y2，…，yn）的樣本均值回歸使殘差平方和最小，即：

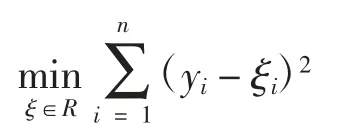
樣本中位數回歸使殘差絕對值之和達到最小，即：

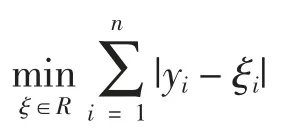
而對于樣本的分位數回歸使加權的殘差和達到最小，即：

上式可以等價表示為：

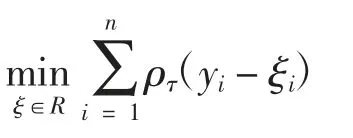
式中：ρτ（u）為檢驗函數，定義為ρτ（u）=u（τ-（Iu ＜0））。

對于條件分位數，可以將條件分位數表示為Qy（τ|x）=xTβ（τ）并且可以通過求解來得到（τ），即：

對于模型（2）中回歸系數的解為：

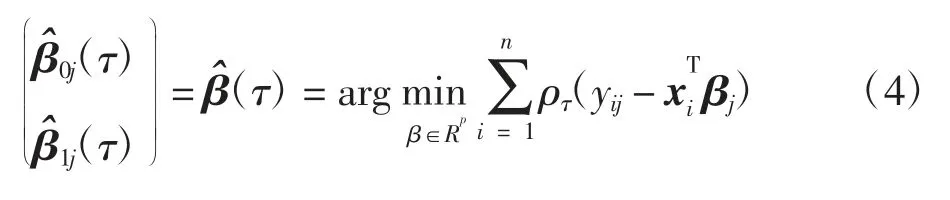
3 基于分位數回歸的變點控制圖

觀測數據集為m 個隨機樣本，每個樣本由nj對觀測序列（xij，yi）j組成，i=1，2，…，n；j=1，2，…，m。解釋變量X 和響應變量Y 之間的關系用模型（2）來表示，并假設模型中εij項是獨立同分布于N（0，1）的隨機變量，進一步假設模型中的設計陣X 已知，且每個樣本中的x 值相同。如果過程是穩定的，那么回歸系數滿足為了監測線性函數型數據集中的回歸系數變化，將m個樣本所有觀測值合并成一個容量為N 的樣本，然后用對合并后的樣本進行分段回歸。如果樣本中存在多變點，那么當監測到一個變點后，可以用二分法來繼續尋找其他的變點，直到沒有變點出現。假設從第m1（m1=1，2，…，m-1）個函數型數據之后回歸模型系數中存在變點，那么有以下假設。

假設1

H1：存在一個（jj=1，2，…，m-1），使得

假設2

H1：存在一個（jj=1，2，…，m-1），使得

為了檢驗上述假設，構造以下似然比檢驗統計量：

可控狀態下，式（5）中的lrt m1（τ）統計量在m1取值不同時，其期望值也不同，模擬可控狀態下τ 取0.5和0.9 時的lrt m1（τ）統計量的期望值如表1 所示。模擬的可控模型中系數取值為β0=0，β1=1，即模型為yij=xi+εij（i=1，2，…，n；j=1，2，…，m）。其中n=10，m=20，解釋變量X 的取值為0（0.2）1.8（即0～1.8，間隔為0.2）。假設εij是獨立同分布于N（0，1）的隨機變量。

表1 模擬可控狀態τ 下取0.5 和0.9 時的lrt m1（τ）統計量的期望值

正如表1 所示，m1取值不同時E（lrt m1（τ））的值也不同，用lrt m1（τ）除以歸一化因子Cm1（τ）矯正lrt m1（τ）使得對于不同的m1值似然比檢驗統計量的期望值是一致的。如果令Cm1（τ）=E（lrt m1（τ）），則修正后的統計量為：

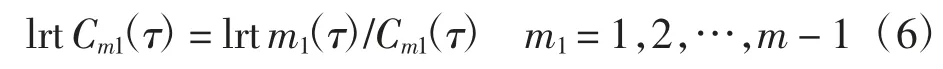
然后在第I 類錯誤概率α 給定的情況下，通過模擬近似給出修正后的lrt 統計量的閾值。

4 模擬研究控制圖表現

使用R 軟件進行模擬，可控模型中系數取值為β0=0，β1=1，即模型為yij=xi+εij，其中i=1，2，…，n；j=1，2，…，m；n=10；m=20。假設εij是獨立同分布于N（0，1）的隨機變量。解釋變量為固定樣本，這里假設解釋變量X 的取值為0（0.2）1.8（即0～1.8，間隔為0.2）。取分位數τ 為0.5 和0.9，使用式（6）中的似然比檢驗統計量通過10 000 次模擬在第Ⅰ類錯誤概率為0.04 的情況下，產生的閾值分別為7.36 和22.02。在模擬中所研究的漂移類型是在樣本q（q ＜m）之后發生的持續性漂移，假設漂移發生在樣本q=15，18 和19之后，截距和斜率項分別以為單位，其中將加了漂移的似然比檢驗統計量與閾值比較，如果大于閾值，就記為一次成功，運行上述程序10 000 次，能準確識別變化的概率稱為整體失控報警概率。

截距從β0漂移到的失控報警概率如圖1 所示。圖1（a）和（b）分別給出了τ 取0.5 和0.9時截距在樣本q=15、18 和19 之后（q ＜m）從β0漂移到情況下的整體失控報警概率，其中λ取0.5（0.5）5（即0.5～5 間隔為0.5）。從圖1 可以看出，本文提出的變點法在q 取某一值的情況下，監控大的漂移比監控小的漂移好，在漂移取固定值時q 取值越小變點法的監控表現就越好。但當q 值取19 時，從圖1 中可以看出變點法的監控效果明顯弱于q 取其他值的監控效果。

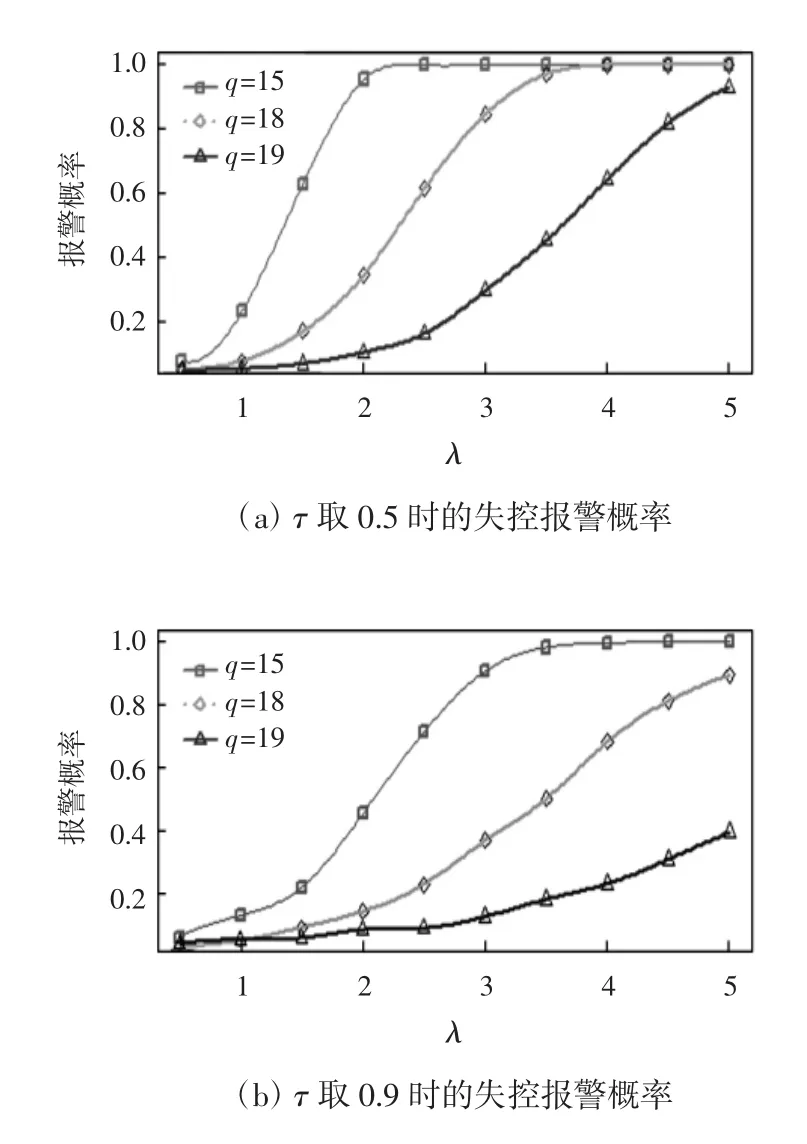
圖1 截距從β0 漂移到β0+λσ/的失控報警概率

斜率項從β1漂移到的失控報警概率如圖2 所示。圖2（a）和（b）分別給出了取0.5 和0.9時斜率在樣本q=15、18 和19 之后（q ＜m）從β1漂移到情況下的整體失控報警概率，其中δ取從圖2 可以看出，對于監控這種類型的漂移結果與監控截距項結果一致，都是在q 取某一值的情況下，監控大的漂移比監控小的漂移好，在漂移δ 取固定值時，q 取值越小變點法的監控表現就越好，但是當δ 取值足夠大時，即截距項發生大漂移時，無論q 取何值，變點法的監控結果都令人滿意。

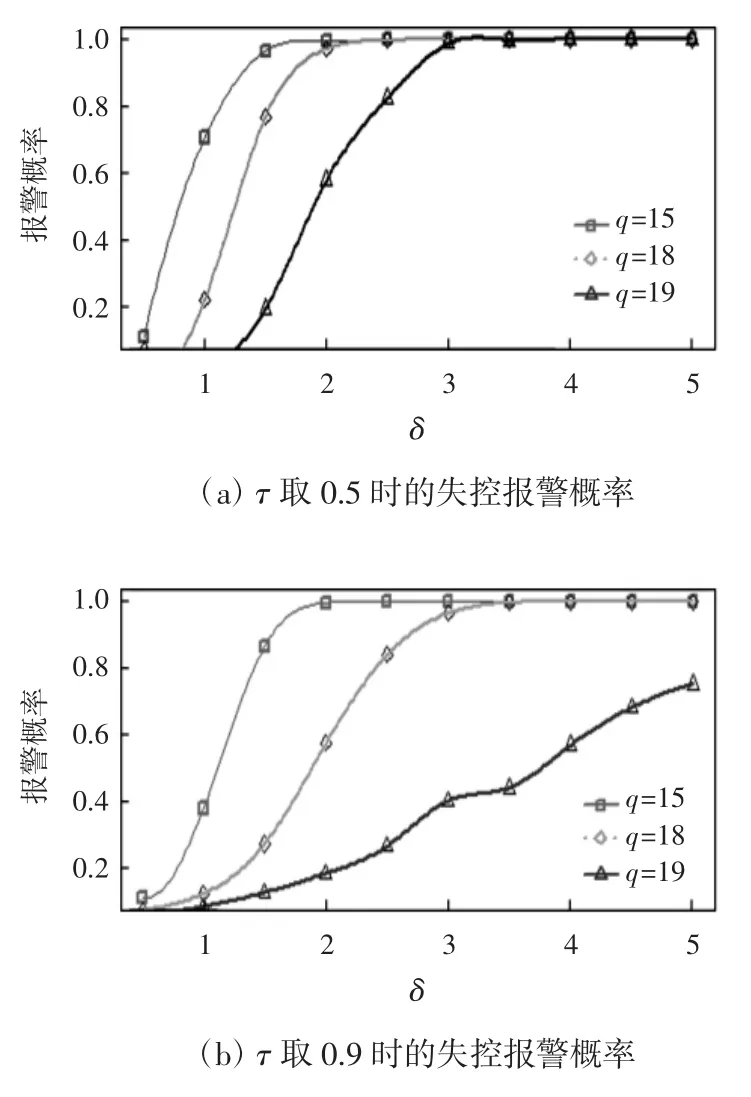
圖2 斜率項從β1 漂移到β1+δσ/的失控報警概率

截距項從β0漂移到以及斜率項從β1漂移到的失控報警概率如圖3 所示。圖中給出了τ 取0.5 時在樣本q=2 和10，截距項從β0漂移到情況下的整體失控報警概率和斜率項從β1漂移到的失控報警概率。從圖3 中可以看出，變點控制圖監控截距漂移過程并不理想，在q 值取2 或者更大值時，依然無法準確監測到變點，而對于斜率項的漂移來說，變點法可以監測出變點，但效果不如監控持續性漂移好。

由圖1 和圖2 可知，本文提出的基于分位數回歸的變點法控制圖可以有效監控系統變化，并且可以說明使用分位數回歸法估計回歸系數的穩健性。

圖3 截距項從β0 漂移到β0+λσ/以及斜率項從β1 漂移到β1+δσ/的失控報警概率

5 結 論

本文研究了函數型數據的變點問題，并提出了基于分位數回歸的變點法，將這種變點法用來監控phaseⅠ中系統變化。通過模擬計算，將監控持續性漂移和非持續性漂移表現進行比較，以及在不同樣本q之后加漂移進行比較。結果表明：無論是持續性漂移還是非持續性漂移，q 值越小變點法的表現越好，而本文提出的變點法在監控持續性漂移表現要比監控非持續性漂移表現效果好；當回歸系數發生較大漂移時，無論q 取何值、漂移類型是持續性還是非持續性，變點法的監控結果都是令人滿意的。