三維MHD方程在BMO空間中的正則性準則

任玉冰， 丁丹丹, 王昌花

(1.山東理工大學 數(shù)學與統(tǒng)計學院，山東 淄博 255049;2.張店區(qū)第九中學，山東 淄博 255040)

1 模型和主要結果

三維MHD方程如下

(1)

式中：u和b分別描述了流體速度和磁場；p是標量壓力項；ν是粘性系數(shù)；η是磁擴散率系數(shù)；u0和b0是給定的初始流速和初始磁場，滿足·u0=·b0=0。

三維MHD方程弱解整體存在性是已知的，但三維MHD方程整體弱解的正則性(即正則性準則)是一個公開的問題。探索和研究方程(1)弱解的正則性影響因素是偏微分方程研究中的重要課題。

He等[1]獲得了關于速度場u的正則性準則：

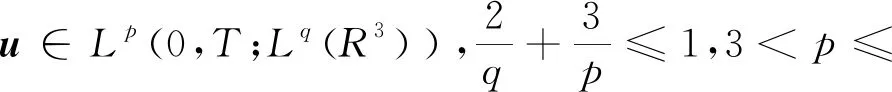
(2)

Ji等[2]證明了正則性準則:

(3)

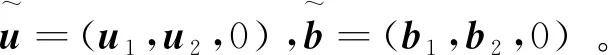
近期還有關于三維MHD方程(1)正則性準則的刻畫[3-4]。

利用能量估計方法和Littlewood-Paley理論，本文進一步研究三維MHD方程在BMO空間中弱解正則性準則的刻畫。主要結果如下：

定理1 設T>0,u0,b0∈H1(R3)且·u0=0,·b0=0。假設(u,b)是方程(1)在R3×(0,T)上的弱解，并且滿足

則下面的不等式成立

注記1式(3)中q,m=時有p,l=2,即研究了，由于LBMO，從而本文的結果推廣了式(3)中的正則性準則。

2 預備知識

為了定義相關空間，本文首先給出Littlewood-Paley分解理論[5]。Littlewood-Paley理論在流體動力學方程中有重要的應用，其中之一是頻率空間的局部化，這種局部化方法的優(yōu)點在于對于其Fourier變換支在球或環(huán)上的分布，可以充分利用Bernstein估計，實現(xiàn)求導或微分運算的代數(shù)化。

設φ、χ分別是支集在C1、C2上的徑向速降函數(shù)類，對于傅立葉逆變換F-1，令

其中

于是定義齊次局部化算子：

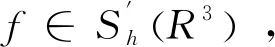
下面給出幾個函數(shù)空間的定義。

定義1 Besov空間

其中

定義2 Triebel-Lizorkin空間

其中

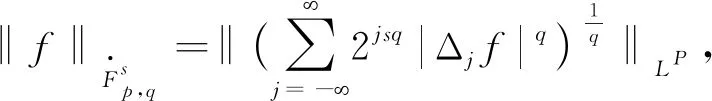
定義3 BMO空間

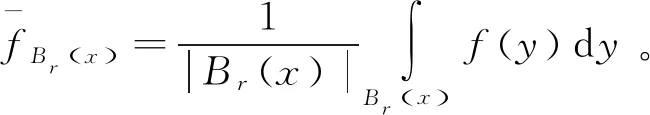
(4)

由式(4)可知

(5)

下面給出本文用到的Bernstein不等式。

引理1假設1≤p≤q≤，對任意函數(shù)f有

其中C是一個獨立于f的常數(shù)。

3 定理1的證明

首先，將方程(1)中前兩個方程兩端分別與Δu,Δb作L2內(nèi)積，有

上述兩式相加可得

(6)

然后對式(6)右端四項分別進行處理。 對于I，利用分部積分法可得

其中

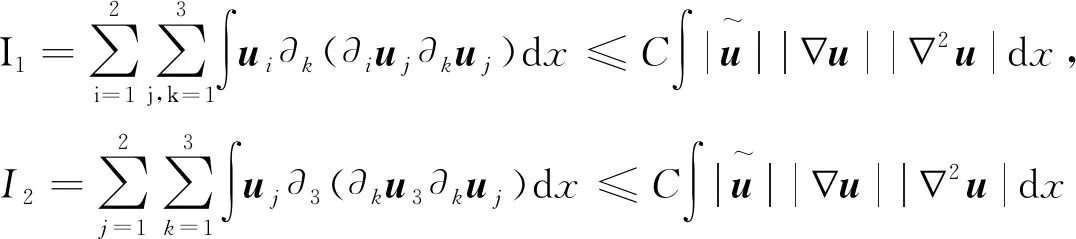
對于I3，由不可壓條件divu=0可知?3u3=-?1u1-?2u2，從而

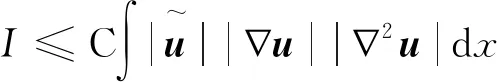
(7)

對于II,利用分部積分法可得

II1+II2

對于III，利用分部積分法可得

對于II2與III2，本文有

此時分別處理II1與III1。對于II1利用與I1相同的方法，可得

(8)

對于III1，利用與I1相同的處理方法，可得

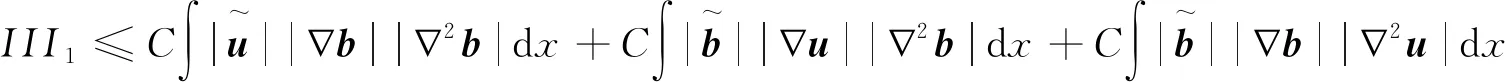
(9)

由式(8)和式(9)可得

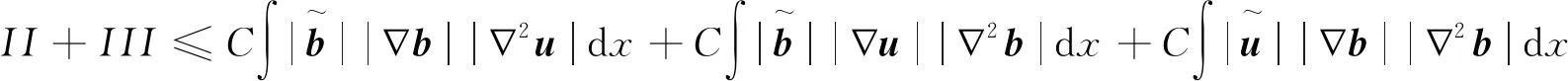
(10)

對于IV， 利用與I相同的處理方法，可得

(11)

將式(7)、(10)和(11)代入式(6)中可得

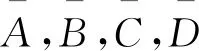
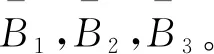
由上式可得

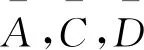
對于合適的整數(shù)N，有

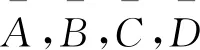
進一步，N滿足如下關系

可以得到

對上式從0到t進行積分并利用Gronwall不等式可以得到

定理1得到證明。