基于高階樸素Bayes算法的電網防誤合故障診斷

遲福建，劉 聰，申 剛，尚德華，呂明琪

(1.國網天津市電力公司，天津 300010; 2.天津天大求實電力新技術股份有限公司，天津 300384;3.杭州師范大學理學院，浙江 杭州 310036)

0 引 言

現代社會中，電網的穩定允許依賴于對故障的準確判斷和預測。輸電線路的故障恢復、防誤合操作等都需要準確的故障診斷。對于不同的電網故障，其所需要的故障診斷的預測時間也存在差異，為實現性能更加優異的輸電線路的故障判斷，需要均衡輸電線路故障診斷的復雜度、診斷精度等性能指標[1-3]。

輸電線路故障診斷過程是利用檢測到的輸電線路故障數據對電網的實時運行情況進行分析和判斷，其準確性與故障診斷方法和模型精度之間存在一定的關聯。常用輸電線路的故障判別算法有神經網絡電網故障判別方法[4]、專家預測電網故障判別方法[5]、最優化計算方法電網故障判別方法[6-7]、Bayes模型電網故障判別方法[8-9]等。文獻[10]采用最優化方法對輸電線路的故障診斷過程進行分析，取得了較好的效果，但是所采用的模型中的有關實踐參量缺乏準確定義。因為輸電網中電氣元件非常多，并且環境各不相同，因此采集到的數據存在較大噪聲，甚至是數據完備性不足，這會導致神經網絡等機器學習獲得的輸電線路故障診斷方法性能存在缺陷[11-12]。與神經網絡等機器學習算法不同，Bayes算法是一種推理算法，具有不確定性特征，其理論基礎是嚴格的概率方法論。Bayes算法中將知識表達成圖形形式進行知識推理，圖形元素之間的關系采用條件概率進行表示，這種不確定形式的結構使該算法更加適用于不確定的輸電線路的故障診斷過程。

本文利用Bayes算法提出一種基于高階樸素Bayes模型的電網系統故障診斷與防誤合策略，給出輸電網模型中電氣元件進行故障分析的Bayes模型結構和電網系統故障診斷與防誤合策略的分析方法。

1 基于Bayes算法的輸電線路故障診斷模型

1.1 電網結構模型

在對發生故障電網進行數據監測過程中，可通過與電力網數據互聯互通實現對輸電網中電器元件參數的實時檢測和記錄[11-12]。首先給出輸電線路模型結構分析示意圖如圖1所示。

圖中，輸電線路的主保護結構包含零序保護和電流的分相保護兩種形式。輸電線路母線上的保護結構包含差動、死區、電流等不同形式的保護結構。符號L與DL分別是輸電線路結構電壓的輸送端口和接收端口。由此可知，圖1所示線路中，變壓器部位的輸電線路保護過程與之相似，輸電線路上變壓器部位主保護的主要作用是保護輸電線路的母線[13]。作為主保護器動作時會激活18DL 、20DL、23DL 、26DL等斷路器。如果這些斷路器發生拒絕動作，那么輸電線路14DL等失靈保護裝置會啟動，自動切除存在問題的線路部分。

1.2 輸電網的Bayes模型構建

對圖1所示的輸電線路故障診斷模型進行精確模型的構建，其包含了圖1中所有的電器元件，如圖2所示。該診斷模型主要由輸電線路保護裝置、輸電線路斷路裝置及其在電路元件之間形成的關系組成。輸電線路上的電氣元件將作為Bayes診斷模型的根節點，節點的運行狀態分為正常和故障兩種，保護裝置和斷路裝置的動作也分為動作和不動作兩種狀態。對于輸電線路故障采集數據的不確定問題，可通過在診斷模型中為每個節點增加附加狀態的形式進行區分，該狀態的識別符為不確定，可采用虛線形式的節點表示。

為提升輸電線路故障診斷的性能，需要對該診斷模型進行量化。節點的概率分布計算需要穩定的電氣元件監測數據，所得故障電氣元件的概率分布形式見表1。保護裝置和斷路裝置的防誤合概率計算情況見表2。

表1 故障電氣元件的概率計算值

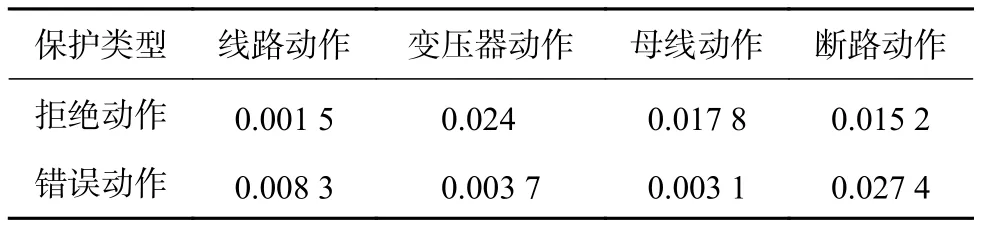
表2 保護裝置的動作狀態計算概率

2 基于HONBM的電網系統故障診斷

2.1 平滑模型優化

基于輸電線路故障診斷模型中電氣元件、保護裝置、斷路裝置的概率計算數值，可同步應用Bayes預測模型進行輸電線路故障診斷模型中節點的概率分布計算。對于診斷模型中虛線形式的節點，因為這些節點的監測數據無法準確獲得，或者數據的完備性較差，在對這些數據節點進行處理時，可以采取忽略的方式進行刪除。

針對以下具有凸屬性的問題進行平滑模型優化分析[13-14]：

其中Q是值域模型上的凸集，其滿足有界性，f(x)也是值域模型上的凸集，其滿足可微性。HONBM方法適合對滿足如下梯度條件約束的問題進行求解：

其中x,x′∈Q。

若凸集函數f(x)符合式(2)所列的限制約束，則凸集函數f(x)具有連續屬性，且為Lipschitz連續梯度，可表示為Hessian模型形式。

HONBM方法的設計思路是對值域中的任何故障數據x(k),y(k)∈Q，生成對應的時間序列：x(0)→y(0)→x(1)→y(1)→x(2)→y(2)→···，并且該時間序列會收斂，其收斂點位置是滿足最優特性。如果當前的迭代計算是x(k)，那么可得y(k)的選取結果為：

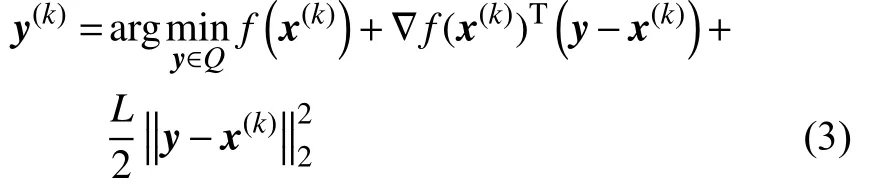
其中，y(k)是凸集函數f(y)在參考點x(k)位置上的近似值，可采用泰勒近似方式獲得，將其表示為凸集函數f(y)的取值上界。由此可得，y(k)是凸集函數上的后續上界取值。然后，基于y(k)以及歷史迭代情況，對x(k+1)進行優化選擇。引入凸集函數f(y)可行集Q上的近似結果，將其表示為d(x)。函數d(x)滿足強凸特性，且強凸函數選取可行集Q上x(0)進行函數值的初始值設定，即取值的最小值。因為函數d(x)滿足強凸特性，則對于值域上的x∈Q，有下式成立：

函數d(x)上的凸性參數是σ，本文利用σ=1進行二次近似：

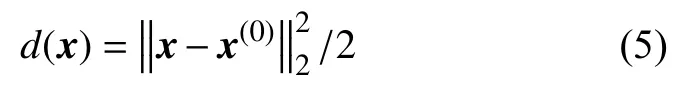
輸電線路故障診斷的Bayes診斷模型的問題模型可表示為[15]：

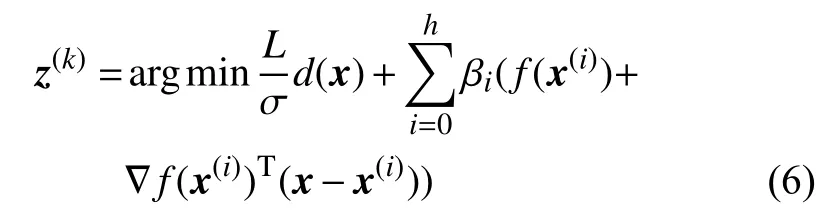
其中βi是輸電線路故障診斷的Bayes診斷模型中的遞增序列，并假定z(k)和y(k)上的凸性函數組合為x(k+1)，形式為：

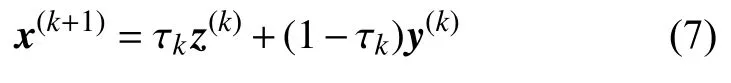
其中τk∈[0,1]。如果{βk}和{τk}選取得當，那么可確保該診斷模型收斂到最優點，得到如下定理。

定理：假設連續函數f(x)是Lipschitz梯度函數，且其取值為恒值L，由此可得，式(3)~(5)中的迭代y(k)，對于設定的條件βk=(k+1)/2和τk=2/(k+3)，存在下列關系成立：

因為選取的可行集Q是有界的，那么可推得也滿足有限性。那么，可得其收斂過程的計算復雜度為在此情形下，需要對式(3)~(5)的計算復雜度進行優化，其中將凸集Q進行目標的分離優化是一種有效的方法。

2.2 輸電線路故障數據的HONBM表示

輸電線路故障診斷的Bayes診斷模型高階關系路徑與圖論模型中的有關定義相似，那么對于非空圖G=(V,E)，利用節點之間的連線可對故障數據之間的關系進行表達，其中V={x0,x1,···,xk}，E={x0x1,x1x2,···,xk-1xk}。

在采用的HONBM模型中，參數估計可基于以下兩個模型公式進行計算：

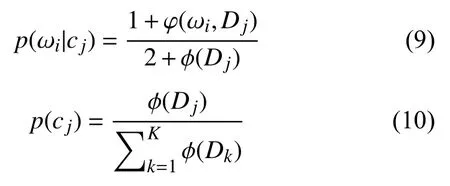
對于給定的輸電線路故障cj，其故障類型高階關系路徑的總數為φ(ωi,Dj)。同時，函數?(Dj)表示輸電線路故障cj中的高階關系路徑的總體數量。式(7)結果顯示所采用的優化方法可有效避免輸電線路故障cj的零概率現象。

2.3 算法描述

首先，將輸電線路的標稱故障屬性轉換為二進制數據。然后，采用以下三分圖形式對輸電線路的標稱故障特征進行表達：

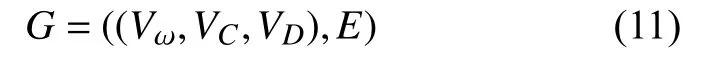
其中VD為頂點對應輸電線路的標稱故障，Vω為頂點對應輸電線路的標稱術語，VC為頂點對應輸電線路的標稱類別。圖3為輸電線路的標稱故障、標稱術語以及標稱類別間的三分圖模型形式。

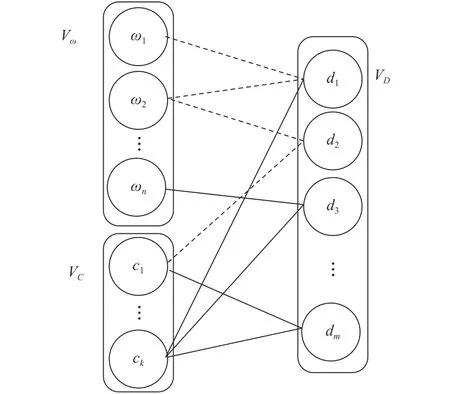
圖3 輸電線路故障的三分圖模型

圖中輸電線路故障的三分圖模型表示方法是一種故障數據的高階表示方法，故障信號集D內的不同電氣元件的關系可利用圖G中子鏈模型進行表示。該子鏈模型通過Vω中故障數據的術語頂點進行啟動，然后利用VD中故障數據的頂點執行數據擴展過程，并且在VC內故障數據的類別節點位置進行終結。關系鏈ωi→ds→ωh→dr→cj所示的故障數據元結構可表示為(ωi,ds,ωk,dr,cj)。該故障數據的關系鏈對應于不同的電氣元件的頂點，可構成一個典型的二階故障數據傳輸路徑。

通過這種數據關系鏈形式表達，可對故障數據的傳輸路徑進行構建。假定?(ωi,cj)是故障信號集D內故障術語ωi及 其所屬類別的關系集，?(Dj)則可表示這種關系集合的匯總，故障信號類別的先驗知識計算形式為：

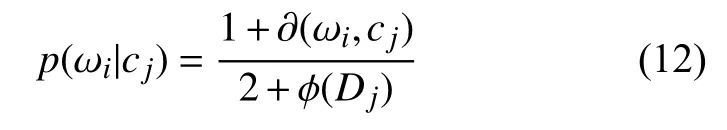
同時，給出輸電線路故障的二階關系路徑計算形式：

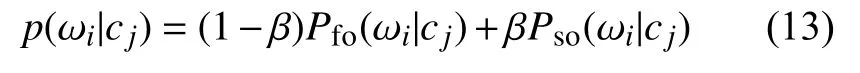
本文中，選取β=0.5。參量Pfo(ωi|cj)中的下標fo指 的是參量Pfo(ωi|cj)的一階路徑計算形式，參量Pso(ωi|cj)中的下標so指 的是參量Pfo(ωi|cj)的一階路徑計算形式。則基于高階樸素Bayes算法的電網系統故障診斷流程如圖4所示。

在以上基于高階樸素Bayes算法的電網系統故障診斷過程中，電網系統故障數據的所屬類別可以利用故障信號的術語矩陣進行表示和存儲。然后，基于二進制形式的故障信號術語矩陣對故障元件的位置進行表達，其中1表示出現故障，0表示正常運行。

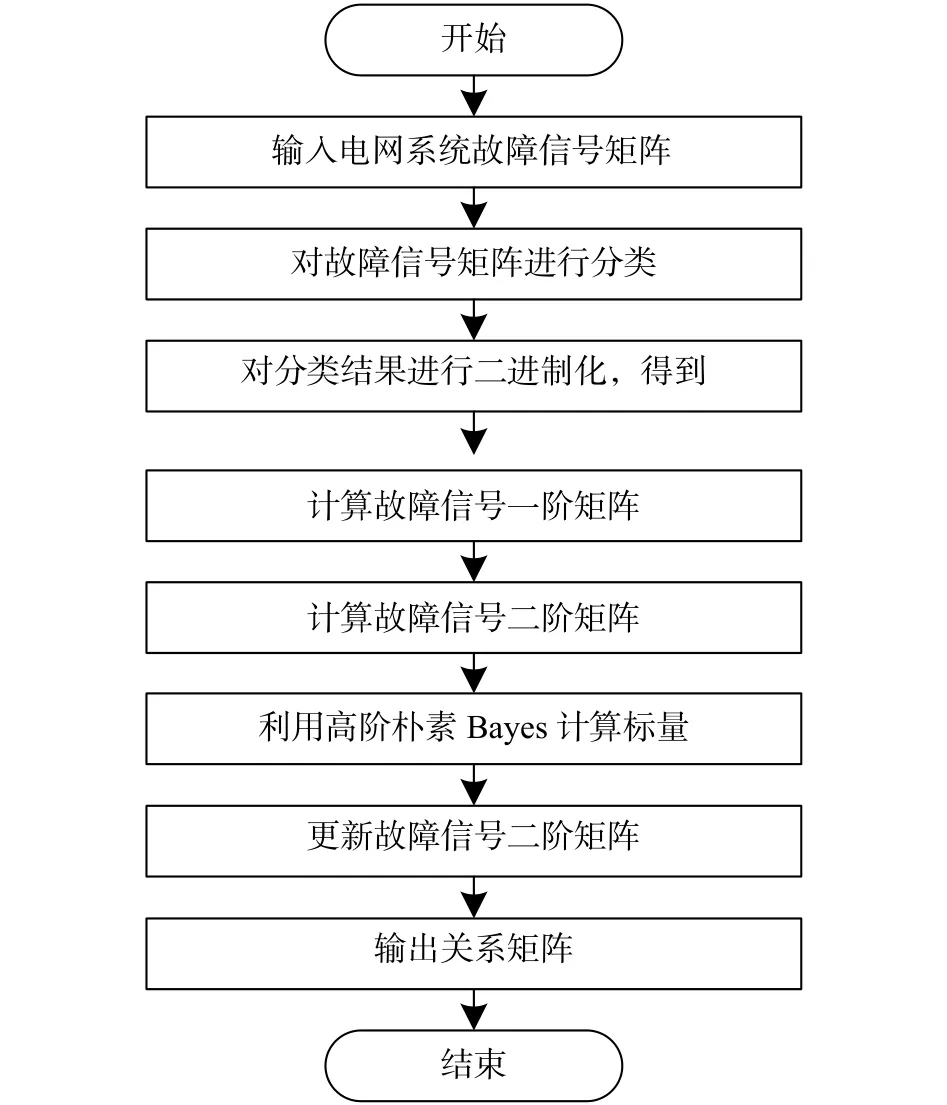
圖4 基于高階樸素Bayes算法的電網系統故障診斷過程

3 實驗分析

本文在對電網系統故障進行實驗中選取的算例見圖5。IEEE14電網算例中的故障點位置為：電網母線B5、L15上存在接地類型故障。相應的保護裝置的動作情況為：斷路器CB2拒絕動作，線路L15、B5上設有后備和主動的保護措施。有關保護動作見表3。

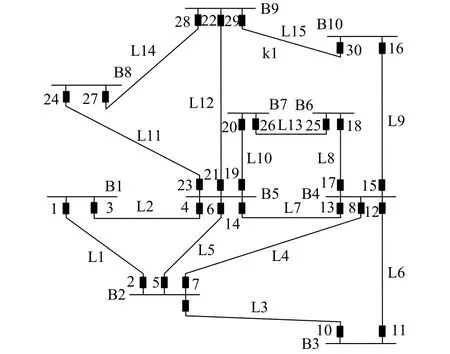
圖5 IEEE14算例

根據上述電網系統故障IEEE14算例的故障設置和線路接線情況分析，發生停電位置的區域中存在的疑似故障電氣元件有B5、L15、L11。對于輸電線路中的母線B5，其執行的保護器操作集可表示為：

表3 有關保護動作

根據輸電線路中發生的故障模式，對母線B5上的故障進行保護，基于高階樸素Bayes算法的電網系統故障診斷過程的節點事件為：

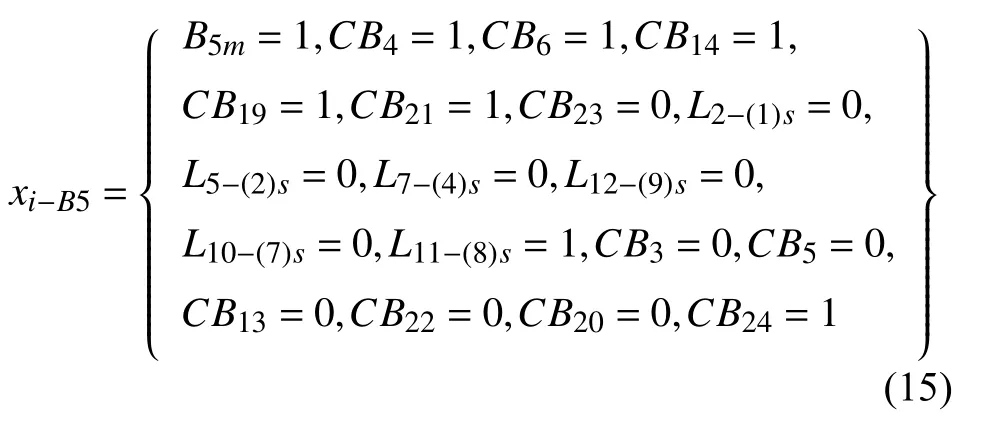
因為基于高階樸素Bayes算法的電網系統故障診斷過程得到的保護動作啟動參數值與發生故障過程中的期望值之間的比值是0.874，該值高于設定的故障閾值0.62，則可判定電網系統故障診斷過程中母線B5上存在故障點。

如果電網系統故障診斷過程出現斷路器動作CB4=1，對其元件故障運行的可信度計算為0.983 7，發生斷路器動作的時間點位于[20:07:19.605, 20:07:19.620]區間內，根據實際設定的時間是20:07:19.607，時間差Δt=10。基于對斷路器動作時間點的可獲得CB4動作的可信度是0.953。由此可得，斷路器動作的可信度計算結果為μ(CB4=1)=0.971。

電網系統故障診斷過程中，線路L15上存在的保護動作集合形式可表示為：

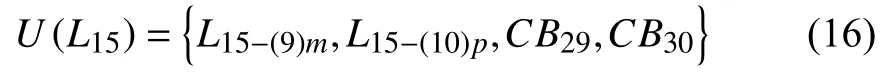
按照對電網系統故障模式的診斷，L15上存在的故障為自給保護故障，利用高階樸素Bayes算法進行模型構建，節點上發生的事件可表示為：

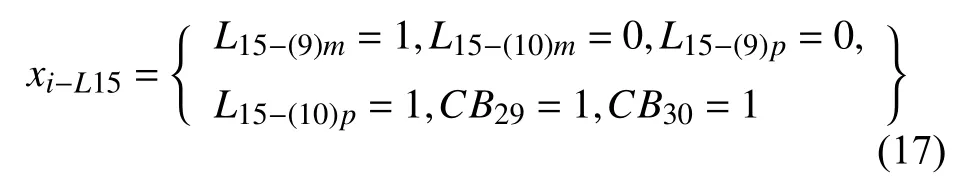
對電網系統故障中節點上存在的動作事件進行相應的可信度計算：

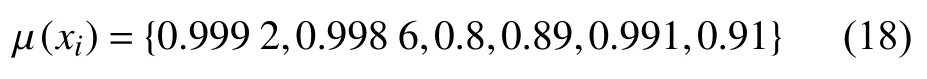
根據上述計算，可得電網系統故障中線路L15發生故障的概率是0.965，因為該值同樣大于設定的故障閾值0.62，那么可判定線路L15上的電氣元件發生故障。對于電網系統故障中線路L11，其在故障出現后產生的動作集為U(L11)={CB24}。根據上述的計算過程，可對采集到的故障信號進行判定，得到線路L11上不存在故障情形，并計算得到線路L11上發生電氣故障的概率比0.001要小，在此情形下可對其故障情形進行判定，為非故障元件。同時，對于電網系統故障中母線B5上出現故障后發生的動作進行匯集，得到動作集U(B5)，該集合包含CB24針對故障的跳閘保護數據信息，由此可得CB24的跳閘保護動作是因為母線B5上發生電氣故障導致的。

由此可得，電網系統故障中母線B5上出現電氣元件的故障情形，CB23對于這種故障是拒絕動作的；電網系統故障中線路L15上存在電氣元件的故障情形，而其上的母線B10位置的保護設備也是拒絕動作的。以上根據基于高階樸素Bayes算法的電網系統故障診斷過程所得的結論與IEEE14算例實際的故障設置情形一致。

在算法對比方面，文獻[11]方法獲得的電網系統故障線路L15上存在電氣元件故障的概率是0.923，與之相比，本文算法得到的概率是0.971，其對于線路L15上存在電氣元件故障的判別更加明顯。此外，本文建立的基于高階樸素Bayes算法的電網系統故障診斷模型，相比于文獻[11]提出的模型方法，構建L11與L15模型更加簡單，在計算用時上，在雙核CPU2.5 GHz主頻下，本文算法計算用時是9.237 ms，而文獻[11]計算用時是19.416 ms，由此可知本文算法的故障診斷效率更高。

4 結束語

本文提出一種基于高階樸素Bayes模型的電網系統故障診斷與防誤合策略。在電網故障診斷中引入Bayes模型結構，實現了電網故障診斷水平的提升；為提高Bayes模型性能，利用高階平滑策略對Bayes模型進行改進；采用IEEE14算例進行算法實現，獲得了較理想的實驗效果。下一步工作將重點研究真實系統的開發，進一步提升算法性能，獲得更理想的故障診斷效果。