變式訓(xùn)練在高中數(shù)學(xué)解題教學(xué)中的應(yīng)用

江蘇省南京市中華中學(xué) 曹曉琰

在傳統(tǒng)的高中數(shù)學(xué)解題教學(xué)過(guò)程中，教師為了在有限的課堂時(shí)間內(nèi)讓學(xué)生掌握更多的數(shù)學(xué)解題知識(shí)，通常都是以概念作為出發(fā)點(diǎn)，運(yùn)用這些概念來(lái)解決數(shù)學(xué)問(wèn)題，但是教師卻忽略了這一階段的學(xué)生思維能力普遍不高的事實(shí)。所以，教師在進(jìn)行數(shù)學(xué)解題教學(xué)時(shí)，不僅要重視數(shù)學(xué)基本知識(shí)的傳授，還要突出解題技巧，應(yīng)該創(chuàng)新解題訓(xùn)練的方法，通過(guò)變式訓(xùn)練把理論與實(shí)踐相結(jié)合，提高學(xué)生的解題能力，達(dá)到“授人以漁”的目的。

一、變式訓(xùn)練中變換條件或結(jié)論

通過(guò)對(duì)數(shù)學(xué)解題問(wèn)題的分析，我們不難看出，不管多么復(fù)雜的數(shù)學(xué)問(wèn)題，它們之間都存在著一定的共性，而且這些共性一般都體現(xiàn)在基礎(chǔ)知識(shí)的運(yùn)用上，所以教師在指導(dǎo)學(xué)生數(shù)學(xué)解題時(shí)，一定要重視變式訓(xùn)練，并通過(guò)變式訓(xùn)練把這些基礎(chǔ)知識(shí)用活、用好、用通，讓學(xué)生在解決實(shí)際數(shù)學(xué)問(wèn)題的過(guò)程中加深對(duì)這些基本知識(shí)的理解，做到“舉一反三”。

例如，在學(xué)習(xí)“函數(shù)的單調(diào)性”時(shí)，有這樣一道題：判斷函數(shù)y=x2+2，x ∈（0，+∞）的單調(diào)性。將該題的條件進(jìn)行變換，則有以下兩種變式，變式一：判斷函數(shù)y=x2+2，x ∈（-∞，0）的單調(diào)性；變式二：判斷函數(shù)y=x2+2 的單調(diào)性。學(xué)生通過(guò)練習(xí)原題與變式一，基本能掌握函數(shù)的單調(diào)性，再進(jìn)行變式二的練習(xí)時(shí)，學(xué)生就會(huì)發(fā)現(xiàn)該函數(shù)不是單調(diào)函數(shù)，若要判斷該函數(shù)的單調(diào)性，則要分段進(jìn)行討論，讓學(xué)生對(duì)函數(shù)的定義加以重視，并能有效地培養(yǎng)創(chuàng)造性思維能力。

二、應(yīng)用變式訓(xùn)練時(shí)變換題設(shè)與問(wèn)題

數(shù)學(xué)學(xué)科作為一門(mén)邏輯性非常強(qiáng)的學(xué)科，在進(jìn)行數(shù)學(xué)解題過(guò)程中沒(méi)有捷徑可走，學(xué)生想要達(dá)到良好的學(xué)習(xí)效果，就必須把基礎(chǔ)知識(shí)進(jìn)行大量的實(shí)際應(yīng)用，從而加深對(duì)這些基礎(chǔ)知識(shí)的理解和掌握，這就需要通過(guò)變式訓(xùn)練最大程度地把自己的“感性”認(rèn)識(shí)變成“理性”認(rèn)識(shí)，從而不斷完善自己的解題思路。

例如，已知集合P={x ∈N|1 ≤x ≤10}，集合Q={x ∈R|x2+x-6=0}，則P ∩Q 等于（ ）

A.{1，2，3} B.{2，3} C.{1，2} D.{2}

解：集合Q={x ∈R|x2+x-6=0}={-3，2}，所以答案為D。

變式：已知集合P={x ∈N|1 ≤x ≤10}，集合Q={x ∈R|x2-5x+6=0}，則Cp(P ∩Q)等于（ ）

A.{1，2，3} B.{2，3}

C.{1，2} D.{1，4，5，6，7，8，9，10}

解：集合Q={x ∈R|x2-5x+6=0}={3，2}，所以答案為D。

分析：上述變式是將問(wèn)題改變，條件改變，是在理解基礎(chǔ)問(wèn)題的前提下，對(duì)最后求解的結(jié)果改變，再求解P 的補(bǔ)集，多了一個(gè)步驟，需要學(xué)生在注意運(yùn)用不等式的時(shí)候，理解集合的運(yùn)用以及補(bǔ)集的運(yùn)用和求解，屬于低等難度。

三、變式訓(xùn)練中變換表達(dá)方式

高中數(shù)學(xué)教師在對(duì)學(xué)生進(jìn)行解題教學(xué)時(shí)，可以通過(guò)變式訓(xùn)練的方式對(duì)學(xué)生的解題能力進(jìn)行訓(xùn)練，教師可以對(duì)題目中的知識(shí)背景不作過(guò)多變動(dòng)，而對(duì)表達(dá)方面的文字描述內(nèi)容進(jìn)行調(diào)整。下面將就這一方面的內(nèi)容進(jìn)行舉例說(shuō)明。

例如，已知存在兩個(gè)點(diǎn)A（-5，0），B（3，0），如果存在一個(gè)移動(dòng)的點(diǎn)M（x，y）與兩個(gè)定點(diǎn)形成的角為90 度，那么M 點(diǎn)的軌跡方程是什么？

變式一：經(jīng)過(guò)A（-5，0）的動(dòng)態(tài)直線與經(jīng)過(guò)B（3，0）動(dòng)態(tài)直線之間形成90 度的直角，那么垂足M 的軌跡是什么？

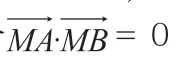
學(xué)生通過(guò)變式訓(xùn)練就能夠發(fā)現(xiàn)，變式后和原題在本質(zhì)上是相同的，僅僅在表達(dá)方面存在一定差異，學(xué)生只要將干擾因素排除，就會(huì)發(fā)現(xiàn)以AB 作直徑的圓即為M 點(diǎn)的運(yùn)動(dòng)軌跡，在兩種變式中，教師就可以引導(dǎo)學(xué)生使用不同的方法進(jìn)行求解，從而讓學(xué)生更好地將理論知識(shí)用于實(shí)際，促進(jìn)學(xué)生思維能力的提高。不難看出，變式訓(xùn)練可以最大程度地發(fā)揮學(xué)生的潛力，使學(xué)生的解題能力得到進(jìn)一步的提升。

總而言之，我們要提高學(xué)生的數(shù)學(xué)能力，不僅要掌握基礎(chǔ)知識(shí)，還應(yīng)該在掌握基礎(chǔ)的概念、定理和公式等基礎(chǔ)知識(shí)之后，熟練應(yīng)用變式教學(xué)，這樣才能在教學(xué)中對(duì)其靈活應(yīng)用，促進(jìn)學(xué)生解題水平的提高。