基于格的可驗證秘密共享方案①

彭 詠,邵培南,李 翔,白建峰,孟珂舉

1(中國電子科技集團公司第三十二研究所,上海 201808)

2(中國科學技術大學 計算機科學與技術學院,合肥 230026)

1 概述

秘密共享最早由Shamir[1]和Blakley[2]與1979年提出.秘密共享方案中存在一個可信的秘密持有者去分離一個秘密到多個不同的子份額.秘密持有者需要將子份額分發給多個子份額持有者.當秘密恢復時,子份額持有者互相交換子份額用于恢復秘密.為了避免子份額的持有者收到錯誤的子份額,可驗證秘密共享允許子份額持有者去驗證自己收到的子份額.后來的可驗證秘密共享方案拓寬了原始的概念,使得可驗證體現在以下兩個方面:

1)秘密分發過程中,子份額持有者驗證從秘密持有者獲得子份額的完整性和正確性.

2)秘密恢復過程中,秘密恢復者驗證從其他子份額持有者那獲得的子份額的正確性和完整性.

秘密共享自提出之后就得到了廣泛關注,并成為眾多論文的研究熱點[3–8].此外,可驗證秘密共享是密碼學方向中的一個重要領域.最早的方案是由文獻[9]提出,用以抵抗非法參與者欺騙攻擊來提高秘密共享方案的安全性.隨后,文獻[10]提出基于文獻[1]的非交互式的可驗證秘密共享方案.該方案利用離散對數的同態性去完成認證.其安全性是基于離散對數的計算難題假設.文獻[11]總結并提出了一種公開秘密共享方案,在其中有一種特別的屬性.任何一位參與者都允許檢查自己收到子份額是不是正確的.

從方案設計角度來看,已經有很多種秘密共享方案被提出.大致可以分為兩類.

第一類,通過通信來完成子份額的驗證.大多數該類方案主要采用雙變量多項式,該類方案主要問題在于,過多的通信導致驗證低效.比如,當n個人參與恢復秘密時,我們需要兩兩驗證子份額的合法性,總共需要進行輪通信.此外,在雙變量多項式的秘密方案中,每個子份額是一個多項式.該類的秘密共享本身從信息率角度來看,即秘密和子份額信息熵的比值,是低效的.它的信息率是該子份額多項式維度的倒數.針對這其中的問題,后來的研究者主要研究如何能夠降低通信復雜度.文獻[12,13]已經展示了如果一個可被忽略的錯誤概率被允許的話,過去的通信復雜度邊界不再適用.文獻[14]在一個可忽略的錯誤概率被允許的情況下,給出了確切的通信輪復雜度.

第二類,采用數學難題來保證驗證的安全性和有效性.很多該類可驗證秘密共享方案,如著名的Feldman[10]和Pedersen[15]都是基于離散對數難題的.該類的方案主要特點,利用公開的參數信息進行驗證,可以做到非交互式的驗證.然而針對離散對數問題和大數分解難題,文獻[16]中Shor給出了一個高效的量子算法.雖然Pedersen[15]更是在Feldman[10]的基礎上,提出了無條件安全的可驗證秘密共享方案,即安全性不依賴于數學難題.即使離散對數能被解決,也能保證子份額的安全性.但一旦出現這種情況,雖然能保證子份額的安全性,但方案將無法保持有效性,驗證的過程可被任意偽造,方案不再有效.

因此,為了應對可能存在的量子計算機,保證方案的有效性,我們需要設計出一種可以抵抗量子攻擊的新型無條件安全的可驗證秘密共享方案.

本論文組織結構如下.在第2節,我們回顧一些基礎的定義,概念和定理.在第3節,提出具體的可驗證秘密共享方案并描述如何進行子份額的驗證.在第4節,分析方案的效率安全性,比較其他的方案.在結束語中做出全文的總結.

2 基礎知識

2.1 秘密共享

定義1.訪問結構

使{p1,···,pn}代表所有參與者的集合.一個集合A?2{p1,···,pn}是單調的如果滿足B∈A 并且B?C,則C?A .一個訪問結構A ?2{p1,···,pn}是集合{p1,···,pn}的非空子集.A中的集合為授權集而任何不在A 均為非授權集合.則A 是該秘密共享方案的訪問結構.

定義2.秘密共享[17]

假定K是秘密s的有限集合.一個分發方案∏ 和集合K實現訪問結構 A 在滿足下列條件下稱之為秘密共享.

正確性:任意在A 中授權集合可以恢復秘密.

隱私性:任意不在A 中的非授權集不能得到關于秘密的任何信息.

2.2 格

格[18]是m維歐式空間Zm的n個線性無關向量組b1,b2,···,bn的整系數線性組合,即:

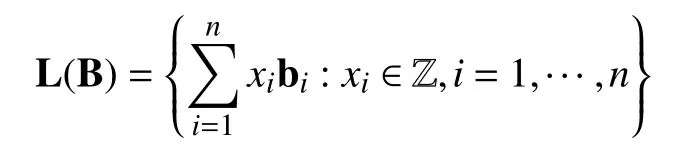
向量組 b1,b2,···,bn稱為格的一組基.同一個格可以用不同的格基表示.m稱為格的維數,n稱為格的秩.有了格的定義,下面我們將簡單介紹格上常見的數學難題,如:最短向量問題,γ-近似最短向量問題(SVPγ),最短線性無關向量問題.這些數學難題,已被用于構造基于格的公私鑰密碼方案.

最短向量問題(Shortest Vector Problem,SVP):給定格 L,找一個非零格向量v,滿足對任意非零向量u∈L,∥ v∥≤∥u∥.

γ-近似最短向量問題(SVP-γ ):給定格L ,找一個非零格向量v,滿足對任意格中的非零向量u ∈L,∥v∥≤γ∥u∥.

最短線性無關向量問題(Shortest Independent Vector Problem,SIVP):給定一個秩為n的 格L,找n個線性無關的格向量si,滿足λi(L)=∥si∥,(i=1,···,n).其中λi(L)表示格L中第i個逐次最小的向量.

2.3 Ajtai單向函數[19]

選定適合的整數q,n,m滿足條件m>nlogq,q=poly(n).令A ∈Znq×m為n×m的矩陣,矩陣中的元素均在 Zq上 .該矩陣包含m個 均勻隨機的向量ai∈Znq,記為A=[a1|···|am],其中{a1,···,am}相互線性無關.

給定函數FA(x)=Ax(modq),x∈{0,1}m,反向計算出原像x的概率是可忽略的,其中,{ 0,1}m表示一個m位的0,1字符串.

上述單向函數的構造十分簡單,且計算十分高效,他的安全性依賴于格難題.根據Ajtai文章[19]中結論,我們有如下引理.

引理1.如果格上的近似最短向量問題(SVP)和近似最短線性無關向量問題 (SIVP)是多項式時間不可解的,對于m>nlogq,q=poly(n),FA(x)是單向函數.

3 方案構造

本節介紹我們提出的可驗證秘密共享方案.該方案示基于Shamir的(t,n)秘密共享,并且具有高效和抵抗量子攻擊的特性.

3.1 符號

首先,定義Fp作為在素數p上的數域.Pi表示第i個參與者,si表示Pi用于恢復秘密的子份額并且si∈Fp.我們使用⊕ 代表異或運算.此外,用A ∈Znq×m表示一個由n個m維 線性無關向量組成的矩陣,其中n,m和q滿足最后,記FA(x)等于Axmodq,其中x∈{0,1}m.

3.2 可驗證秘密共享方案

該方案由以下3個步驟組成:初始化階段,子份額分發階段和秘密恢復階段.

初始化階段:

秘密持有者在Fp上 隨機生成一個t?1 階的多項式f(x):

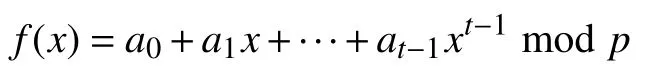
其中,秘密s即為多項式的常數項.也就是說,s=a0.此外,秘密持有者選擇 整 數n,m和q滿足m>nlogq,q=這里我們可以將Fp上的一個元素看成一個m比特的二進制字符串.最后生成m個線性無關的向量αi∈Znq,記為A :=[α1|···|αm].

分發階段:

(1)秘密持有者計算si=f(xi)并且隨機從{ 0,1}m中選擇ti,將(si,ti)一 起發送給子份額持有者Pi.注意到如果sisj且titj,那么si⊕ti一定不等于si⊕tj.

(2)秘密持有者公開矩陣A,FA(si⊕ti)和s′i的值,其中s′i=si⊕ti.

(3)子份額持有者Pi收到(si,ti)后,首先要對自己接收到的子份額進行驗證:

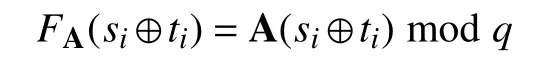
如果驗證所得到的子份額是正確的,那么繼續以下的驟,如果驗證失敗,則要求秘密持有者重新發送子份額.

秘密恢復階段:

假設有k個子份額持有者參與恢復秘密s,其中k≥t,他們需要執行以下步驟:

(1)子份額持有者之間互相驗證對方子份額的合法性,具體操作如下:

如果驗證正確,則繼續下邊的步驟.否則,我們可以通過以下操作檢查每個參與者的身份從而確定哪個是非法的參與者.

(2)參與秘密恢復的子份額持有者互相交換信息si并用所得到這些子份額采用Shamir秘密共享的方式去恢復秘密.

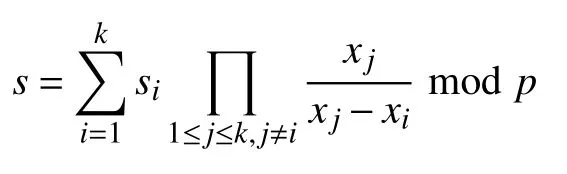
為證明驗證秘密恢復階段步驟(1)的正確性,我們給出定理1.

定理1.單向函數FA具有線性同態的特性,并且滿足以下公式:

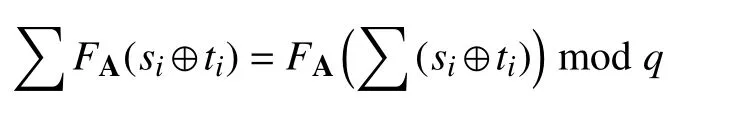
證明:假設有k個子份額持有者組成的授權集合,他們的子份額構成Γ ={s1,···,sk}.每個Γ 中的si均綁定一個對應的隨機值ti,所有的si和ti都 是從{ 0,1}m中選取的.使用 A∈Znq×m表示一個由n個m維線性無關向量組成的矩陣,也就是說A :=[α1|···|αm].那么有:

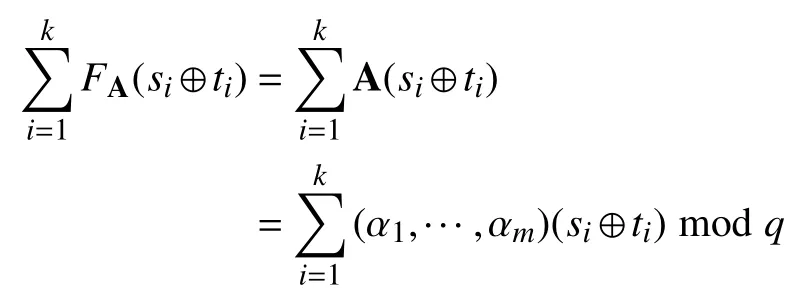
此外,因為 (si⊕ti)仍然是一個m比特位的二進制字符串,可以被寫為因此,上述公式等于:

因此,函數FA有線性同態性并且該定理成立.

4 分析

在本節,我們分析提出方案的效率以及安全性.事實上,我們的方案就是將Ajtai單向函數函數應用到Shamir方案中,同時引入隨機變量ti,使得可驗證方案是無條件安全的.即使最終格難題被破解,也無法獲得關于子份額的任何信息.當然方案的有效性仍然依賴于格難題.

4.1 效率分析

首先,我們需要考慮方案的信息率.信息率是作為衡量一個秘密共享系統的重要手段,被廣泛用于衡量秘密共享方案本身的效率.信息率 σ 被定義為秘密長度與最大子份額長度的比值,也就是說:

在我們的方案中,因為子份額不僅僅是單獨的si,而是一對值(si,ti).因此,該方案的信息率為1/2而不是1.此外,還有以下一些指標用于衡量可驗證秘密共享方案的效率:

(1)驗證子份額時所要通信的輪數.

(2)子份額持有者用于驗證子份額合法性所需的通信數據量.

(3)子份額持有者驗證子份額合法性所要做出的運算量.

指標(1)和(2)用于衡量通信的效率,也是大多數分析通信協議通信復雜度的指標.指標(3)用于衡量計算的效率.

可驗證秘密共享的輪數復雜度主要是在實際方案設計中需要考慮的.通信輪數相較于通信量來言,往往需要更多的時間.因此,在實際的通信協議中往往作為重要因素被考量.我們的方案類似于方案[9,16],是非交互式的可驗證秘密共享,在分發階段,并不需要在驗證時額外交互信息.在秘密恢復時,僅僅只需要將自己的驗證信息廣播出去即可,所以不會提高通信輪數,通信的輪數復雜度可被忽略.

子份額持有者用于驗證子份額合法性所需的比特數可以被分為以下兩部分:秘密持有者分發的信息和子份額持有者之間互相交互的信息.第一部分與其它可驗證秘密共享方案差別較大而后一部分和其它可秘密共享方案大致相同,因此我們主要分析第一部分的信息量.在我們的方案中,秘密持有者需要公開一個矩陣A ∈Znq×m和FA(si⊕ti)的值.它總共包含的比特數如下:

在本文中,計算開銷是可以預估的.為了更好的說明,我們比較我們的方案與其它3篇基于Shamir秘密共享的可驗證秘密共享方案.假設所有的秘密和子份額的空間都是在Fp,我們將Fp上一次乘法運算記為1次運算.

我們只在此比較子份額持有者用于驗證其它子份額合法性所需要的計算量.在我們的方案中,子份額持有者僅僅需要在很小的整數中進行線性運算.總共所需要在Zq中 執行nlogp乘 法運算,其中l ogp>nlogq.為了方便比較計算復雜度,我們通過除以 2n將我們的結果從Zq轉化到Zq.

下面我們將從通訊量,計算量和適用性3個方面,比較本文方案和以往方案.通訊量是秘密恢復階段,每個參與者需要廣播多少比特的驗證信息.計算量是每個在于者在最壞情況的計算復雜度來表示.比較結果如表1所示.

在表1中,Schoenmakers的方案[20]取決于公鑰密碼,所以無法進行評估.此外,我們使用“普適”去代表我們方案的適用性.它代表我們的方案可以應用于任何的方式構造的秘密共享方案中,例如基于拉格朗日插值多項式,基于中國剩余定理,基于超平面空間,基于線性碼等密碼共享方案.顯然,我們的方案相對于其它可驗證秘密共享方案具有更好的計算效率.

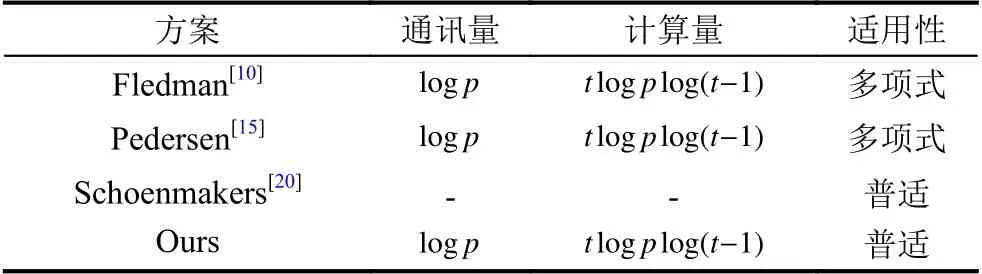
表1 本方案與已有方案的性能比較

4.2 安全性分析

我們的方案是基于Shamir秘密共享,所以任何授權集合都應該能夠恢復秘密而任何的非授權集合都不應該能恢復秘密.此外,我們還需要考慮驗證過程的安全性,也就是說子份額持有者在驗證子份額合法性時是否泄漏了秘密.

定理2.本文方案的驗證機制,包括分發和秘密恢復過程,基于Ajtai單向函數,滿足不可區分和不可偽造特性.

證明:在我們的方案中,si⊕ti滿足均勻隨機分布.此外,Ajtai單向函數FA(si⊕ti)是均勻隨機分布.我們不能夠區分所以該驗證機制滿足不可區分的特性.

為了證明綁定特性,我們需要證明不存在 概率多項式時間的算法去找到兩個不同的si.也就是說,不存在 概率多項式時間的算法去找到sisj∈{0,(1}m使)得Asi≡Asj(modq).如果我們找得到,那么存在0(modq).因為sisj∈{0,1}m,我們有構成了一個針對格難題中小整數問題的一個解法,而小整數問題被認為是一個不可解的數學難題.因此,本方案中驗證機制滿足不可偽造性.

我們已經證明了我們方案的驗證機制滿足不可區分和不可偽造兩個特性.不可區分特性意味著方案的驗證過程不會泄露秘密的任何信息.不可偽造特性意味著只有正確的子份額才能通過驗證.在上述證明過程中,不可區分和不可偽造均是依賴于格難題.

定理3.即使Ajtai單項函數被破解,驗證子份額的過程也不會泄露任何秘密的信息.

證明:根據引理1,我們知道Ajtai單項函數可以被約簡為格難題中的近似最短線性無關向量問題.至今還沒有任何多項式時間的算法去解決近似最短線性無關向量問題.假設近似最短獨立向量問題和Ajtai單項函數都被破解,攻擊者可以從FA(si⊕ti)得 到值si⊕ti.因為ti是 在子份額空間中的隨機值,所以si⊕ti是隨機分布在子份額空間的,從而我們無法從si⊕ti得到任何秘密的信息.這就表明了,即使Ajtai單項函數被破解,驗證子份額的過程也不會泄露任何秘密的信息.

通過以上證明,我們得到我們的方案是無條件安全的.換言之,格難題保證了可驗證的有效性,即使格難題被破解,我們的方案依舊不會泄露子份額的任何信息.即本方案的驗證機制是無條件安全的.

5 結束語

我們在本文展示了基于格的可驗證秘密共享方案,能夠在秘密分發和恢復過程中,驗證子份額的合法性.同時該方案具備無條件安全的特性,即使格難題被其他什么未知工具破解,也能保證子份額的安全性.

本方案通過與已有方案的比較,我們的方案具有以下特性:更高的效率;量子攻擊抵抗性;普適性(可以應用于任何數學工具實現的秘密共享方案).