基于一致性局部調整算法和DEA的語言偏好決策模型
金飛飛,倪志偉,陳華友,朱旭輝,武文穎
(1.安徽大學商學院,安徽 合肥 230601;2.合肥工業大學管理學院,安徽 合肥 230009;3.過程優化與智能決策教育部重點實驗室,安徽 合肥 230009;4.安徽大學數學科學學院,安徽 合肥 230601)
1 引言
決策作為現實生活中最常用的一種活動,已經廣泛應用于各個領域[1]。由于實際決策問題具有模糊性、不確定性等特征,再加上人類思維存在局限性,使得許多決策信息不能簡單地運用精確值進行描述[2]。對此,Zadeh提出模糊集理論[3],其運用隸屬度來描述集合中元素的模糊性。在決策過程中,專家們通常將一組備選方案進行兩兩比較后給出相應的評價信息,從而構造包含決策信息的偏好關系。模糊偏好關系[4-5]和乘性偏好關系[6-7]是兩種最為常用的偏好關系形式。然而上述這些偏好關系的一個共同點就是評價信息均是用數字進行表達,而語言信息能夠貼近于人類的認知,所以運用語言變量表達決策者評估信息更為合理和直觀。因此,Zadeh[8]于1975年提出了模糊語言方法。隨后,專家們引入語言偏好關系[9-11]的概念用于對決策信息進行更為直觀和定性的表達。
由于運用缺乏一致性的偏好關系進行計算容易導致出現不合理甚至錯誤的決策結果[12]。因此,一致性分析和排序權重的確定是研究偏好關系的兩個主要課題。為了探究偏好關系的基本性質和特征,Xu Zeshui[4]對現有偏好關系進行了總結研究,并提出了幾類新的偏好關系。Herrera-Viedma等[13]詳細分析了模糊偏好關系一致性的特征性質,然后設計了一種基于原始數據構建具有一致性的模糊偏好關系方法。針對評價信息為直覺模糊數的群決策問題,Jin Feifei等[14]首先定義了直覺模糊偏好關系的有序一致性和乘性一致性概念,設計了一種乘性一致直覺模糊偏好關系與直覺模糊權重向量進行相互轉化的方法,進而建立了兩種群決策方法用于確定方案的排序權重向量。Xu Zeshui和Liao Huchang[15]針對直覺模糊偏好關系的概念、一致性、相容性以及排序方法等進行了全
面的總結和分析。在猶豫模糊信息環境下,Zhang Zhiming等[16]構建了一個包含有一致性迭代改進過程、相容性實現過程以及方案選擇過程的決策支持模型。針對決策者給定的猶豫模糊偏好關系,Zhu Bin等[17]提出一種基于最優化模型的乘性一致性迭代調整算法,使得調整后的猶豫模糊偏好關系具有滿意一致性。Zhang Zhiming和Wu Chong[18]基于猶豫乘性偏好關系的一致性計算區間排序權重向量,進而對方案進行排序。Wu[19]提出了一種整合DEA和模糊偏好關系的模型得到方案排序,并構造一種交叉評估模型。Lin Yang和Wang Yingming[20]將DEA引入到猶豫乘性偏好關系中,設計了兩種優先排序方法。
近年來,對語言偏好關系及其拓展形式的一致性和排序權重確定方法的研究也越來越受到學者們的專注[21-22]。針對不一致的語言偏好關系,Jin Feifei等[23]研究了基于自迭代模型和基于最優化模型的加行一致性調整算法對原始語言偏好關系進行調整,從而使得調整后的語言偏好關系具有滿意一致性。Dong Yucheng等[24]提出一種基于最優化模型的算法用于改進非對稱語言偏好關系一致性水平,從而使得原始語言偏好關系中的決策信息能夠得到盡可能多的保留。雖然對語言偏好關系的研究越來越深入,但是現有的很多語言偏好關系模型方法存在著一些不足。借鑒于模糊偏好關系的乘性一致性定義,Jin Feifei等[25]提出了語言偏好關系乘性一致性的概念,其揭示了乘性一致語言偏好關系與排序權重向量之間的內在聯系,然后以最小化偏差為準則建立最優化模型,構建具有收斂性的語言群決策迭代算法計算出排序權重向量,并通過對供應鏈中供應商的選擇算例驗證了提出的群決策模型是科學有效的。Zhu Bin和Xu Zeshui[26]在首次定義猶豫模糊語言偏好關系的概念之后,提出了一系列的猶豫模糊語言偏好關系一致性度量方法,并分別建立了基于最優化模型和基于反饋機制的收斂迭代算法用于提高猶豫模糊語言偏好關系的一致性。針對非加性一致性的猶豫模糊語言偏好關系,Wu Zhibin和Xu Jiuping[27]定義了新的一致性指數公式,并基于猶豫模糊語言偏好關系對應的二元語言偏好關系和加行一致語言偏好關系,建立了一種新的一致性迭代調整算法,該算法雖然能夠對非一致性程度最大的元素進行調整,但是調整的幅度太大,容易丟失過多的原始決策信息。對于非乘性一致性的猶豫模糊語言偏好關系,Zhang Zhiming和Wu Chong[28]首先將其轉化為標準的猶豫模糊語言偏好關系,然后設計一種具有收斂性的自動迭代算法對標準的猶豫模糊語言偏好關系進行調整,使得修復后的猶豫模糊語言偏好關系達到一致性閾值。Pei Lidan等[29]基于加性一致直覺模糊語言偏好關系與直覺模糊權重向量之間的關系,建立了一種基于最優化模型的自迭代決策方法,該方法不僅能夠提高直覺模糊語言偏好關系加性一致性,還可以幫助決策者獲得合理可靠的決策結果。Xu Zeshui[30]直接運用提出的語言算術平均算子對語言偏好關系進行信息融合的計算。然而,運用非一致性的語言偏好關系進行計算容易出現非一致的決策結果。因此,運用Xu Zeshui[30]中的方法計算得到的決策結果不一定合理可靠。針對非一致性的語言偏好關系,Dong Yucheng等[31]建立了一種一致性改進算法用以提升原始語言偏好關系的一致性水平。但是在調整的過程中,通過該算法生成的具有加行一致性的語言偏好關系相較于原始語言偏好關系有了較多元素和較大幅度的改變,從而造成原始決策信息的大量丟失,迭代過程中生成新的語言偏好關系的決策過程隨機性太強。針對不具有滿意加性一致性的不確定二元語言偏好關系,Zhang Zhen和Guo Chonghui[32]首先提出了一種加行一致不確定二元語言偏好關系的構建方法,然后設計了新的加性一致性迭代算法對原始的不確定二元語言偏好關系進行提升。然而,運用Zhang Zhen和Guo Chonghui[32]的調整算法每進行一次迭代,都需要對原始的不確定二元語言偏好關系的大部分信息進行調整,同時構建得到的加行一致不確定二元語言偏好關系中的元素可能不在規定的語言術語集領域之內。(具體可見案例分析部分)。
針對上述問題,本文提出了構造乘性一致語言偏好關系的方法,為了盡可能保留原始決策信息,引入局部調整策略,設計了一種具有收斂性的乘性一致性改進算法,使得改進后的語言偏好關系具有滿意乘性一致性。隨后,基于DEA模型建立了最優化模型,進而確定方案的排序權重向量。最后,構建一個基于一致性局部調整策略和DEA方法的語言決策模型,從而得到合理可靠的決策結果。
2 基本概念
假設S={s0,s1,…,s2τ}是一個元素個數為奇數且全排序的語言術語集[8],其中si表示語言變量,2τ+1表示語言術語集S的基數。這里τ是一個正整數,那么2τ為一個偶數,并且2τ的取值必須滿足以下條件:(i)能夠避免語言術語集S中的元素個數過多而造成對決策專家施加無用的精度;(ii)語言術語集S中的元素必須足夠豐富,以便允許在有限數量的評價等級中辨別或區分每個評價對象的優劣性能。因此,通常情況下,語言術語集S的基數2τ+1取值7或9,通常不超過11[33]。語言集S需要具有以下兩個特征:(1)若α≥β,則sα≥sβ。因此,存在最大最小算子;(2)存在逆算子:neg(sα) =s2τ-α,特別的neg(sτ)=sτ。
例1 為了描述一座房屋外觀,決策者可利用語言集S={s0:極差,s1:很差,s2:差,s3:稍差,s4:一般,s5:稍好,s6:好,s7:好,s8:極好}中的語言變量進行評價。

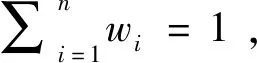
定義1[23]:假設X={x1,x2,…,xn}是一個方案集,定義在X上的判斷矩陣A=(aij)n×n是一個語言偏好關系,其中aij∈S且
aij+aji=s2τ,aii=sτ,?i,j∈N
(1)
這里aij表示方案xi相對于xj的語言偏好度。特別的,當aij=sτ時,表示xi與xj間無差異;當aij>sτ時,表示xi優于xj;aij越大表示xi相對于xj越優;當aij=s2τ時,表示xi完全優于xj。
定義2[4]令A=(aij)n×n是定義在X上的語言偏好關系,那么A=(aij)n×n具有乘性一致性,如果其滿足如下乘性傳遞性:
I(aij)I(ajk)I(aki)=I(aik)I(akj)I(aji),i (2) 定義3[12]:令A=(aij)n×n是定義在X上的語言偏好關系,那么A=(aij)n×n具有乘性一致性,如果存在一個排序權重向量w=(w1,w2,…,wn)Τ,使得: (3) 本節主要研究如何構造乘性一致語言偏好關系,然后設計一種基于局部調整策略的一致性改進算法,并證明算法的收斂性。 定理1假設A=(aij)n×n是定義在X上的語言偏好關系,其中aij∈S,那么下面命題等價: (i)A具有乘性一致性。 證明:(i)?(ii) 因為命題(ii)可以轉化為:當 I(aij) (4) 因此只需證明當A具有乘性一致性時,公式(4)成立即可。 因為i,j∈N,i I(ai,i+k) (5) 接下來將運用數學歸納法證明公式(5)成立。當k=1時,則顯然有: 假設當k=l時公式(5)成立,則有: I(ai,i+k) (6) 當k=l+1時。由于A具有乘性一致性,則有 I(aij)I(ajk)I(aki)=I(aik)I(akj)I(aji),i 于是對于i I(ai,i+l+1)I(ai+l+1,i+l)I(ai+l,i) =I(ai,i+l)I(ai+l,i+l+1)I(ai+l+1,i) 所以I(ai,i+l+1)·(2τ-I(ai+l,i+l+1))·(2τ-I(ai,i+l))=I(ai,i+l)·I(ai+l,i+l+1)·(2τ-I(ai,i+l+1)),從而有: I(ai,i+l+1)={2τ·I(ai,i+l)·I(ai+l,i+l+1)}/I(ai,i+l)·I(ai+l,i+l+1)+(2τ-I(ai,i+l))(2τ-I(ai+l,i+l+1)) (7) 于是證明了當k=l+1時,公式(5)成立。 (ii)?(i) 根據上述證明過程可知,命題(ii)可轉化為公式(4)。令i I(aik) (8) I(akj) (9) I(aij)I(ajk)I(aki)=I(aij)·(2τ-I(akj))·(2τ-I(aik)) (10) I(aik)I(akj)I(aji)=I(aik)·I(akj)·(2τ-I(aij)) (11) 因此I(aij)I(ajk)I(aki)=I(aik)I(akj)I(aji),i 依據定理1,容易得到如下結論成立,即: 定理2假設A=(aij)n×n是定義在X上的語言偏好關系,其中aij∈S,令 (12) 根據定理2可以得到如下推論。 (13) 根據公式(13)顯然有CI(A)∈[0,1]。CI(A)的值越小表示A的一致性程度越高。如果CI(A)=0,則表示A具有完全乘性一致性。 對于非滿意乘性一致性的語言偏好關系A=(aij)n×n,接下來將運用局部調整策略設計一種一致性改進算法,使得改進后的語言偏好關系不僅具有滿意乘性一致性,而且使得原始的語言偏好關系A=(aij)n×n中元素變化程度最小,從而最大程度保留原始的決策信息。 基于局部調整策略的一致性改進算法設計如下: 算法 I (14) (15) 令t=t+1,返回步驟2。 步驟7結束。 接下來將證明上述迭代算法是收斂的。 (16) CI(A(t+1)) (17) 綜上,定理3結論成立。 本節首先提出一種基于DEA的權重確定方法,探究方案的相對效率得分與排序權重向量之間的關系,然后構建新的語言決策模型,最終得到合理可靠的決策結果。 在決策問題中令X={x1,x2,…,xn}是一個有限方案集,A=(aij)n×n是定義在X上的語言偏好關系。基于DEA理論,在決策過程中可將每個方案xi看成是一個獨立的決策單元DUMi。通常情況下,如果備選方案xp優于xi,即xp?xi,那么在語言偏好關系A=(aij)n×n中的信息就表現為apk≥aik,k∈N,即I(apk)≥I(aik),k∈N,這符合DEA模型產出變量的特征。因此,A=(aij)n×n的每一列可以看成是一類產出。另一方面,由于DEA模型在構建的過程中通常要求決策單元DUMi必須具有投入變量,因此,為了保證決策的公平性,在模型的構建過程中本文賦予所有決策單元相同的虛擬輸入變量sτ,那么基于語言偏好關系A=(aij)n×n,可以得到如下的DEA投入產出表(見表1)[19,34]。 于是可以構建如下產出導向的DEA模型用于計算決策單元DUMi(i∈N)(即方案xi)的相對效率: maxβi (18) 在模型(18)中,本文基于所有決策單元構建了一個虛擬的組合單元,其中up表示構建虛擬組合單元是決策單元DUMi所占的比例。模型(18)表示虛擬組合單元在最多消耗與決策單元DUMi相同投入量sτ的前提下,至少輸出決策單元DUMi產出的βi≥1倍。 maxβi (19) (20) (21) 通過結合公式(20)和(21)可得 (22) 則有 (23) 再將公式(23)帶入到公式(22)可得 (24) 綜上,定理4結論成立。 對于給定的語言偏好關系A=(aij)n×n,接下來將運用一致性改進算法和權重確定方法得到決策方案的可靠排序,最終遴選出最優方案。 算法 II Input: 原始語言偏好關系A=(aij)n×n. 第二階段:根據最優化模型(18)的目標函數值和定理4,確定方案的排序權重w=(w1,w2,…,wn)Τ。 第三階段:依據排序權重wi(i∈N)的大小對方案xi(i∈N)進行優劣排序,并輸出選擇最佳方案。 第二階段:利用MATLAB計算最優化模型(18)的最優目標函數值,并運用定理4得到供應商對應的排序權重向量:w=(w1,w2,w3,w4)T=(0.5413,0.2313,0.1575,0.0699)T。 第三階段:由于w1>w2>w3>w4,所以x1?x2?x3?x4,于是綜合性能最佳的供應商為x1。 基于一致性局部調整策略和DEA的語言決策模型不僅能夠在最大程度保留原始決策信息的基礎上將原始語言偏好關系調整為具有滿意乘性一致性的語言偏好關系,而且能夠通過DEA模型得到方案的排序權重。接下來,為了說明本文方法的有效性,將運用現有的語言決策方法處理上述問題。 Xu Zeshui[30]基于提出的語言算術平均算子處理上述問題的大致過程為:首先運用語言算術平均算子計算得到四個供應商對應的綜合語言偏好信息: a1=s4.350,a2=s4.075,a3=s3.300,a4=s4.275。 因為a1>a4>a2>a3,所以供應商的優劣順序為x1?x4?x2?x3,并且綜合性能最佳的供應商為x1。 Dong Yucheng等[31]研究了加行一致性語言偏好關系的改進算法,以使得改進后的語言偏好關系達到一致性閾值水平。運用文獻[31]中算法處理上述供應商選擇問題的主要步驟如下: V(0)= 步驟4:利用語言算術平均算子計算四個供應商對應的綜合語言信息分別為: 針對不具有滿意加性一致性的不確定二元語言偏好關系,文獻[32]首先提出了一種加行一致不確定二元語言偏好關系的構建方法,然后設計了新的加性一致性迭代算法對原始的不確定二元語言偏好關系進行提升,最后運用二元語言算術平均算子得到供應商的綜合偏好信息。運用文獻[32]中算法4.1處理上述供應商選擇問題的主要步驟如下: 步驟1’:將語言偏好關系A=(aij)4×4轉化為如下二元語言偏好關系B=(bij)4×4: B= 步驟4’:運用二元語言算術平均算子計算得到四個供應商對應的綜合語言信息分別如下: 分析上述對比實驗過程和結果,本文提出的基于一致性局部調整策略和DEA的語言決策模型具有以下優勢: (1)運用本文建立語言決策模型計算得到的最佳供應商與利用文獻[30]、文獻[31]和文獻[32]中算法4.1得到的決策結果相同,這說明了提出的語言決策模型是合理的。 (2)眾所周知,運用不具有滿意一致性的語言偏好關系容易得到非一致的決策結果。然而,文獻[30]在沒有對語言偏好關系進行一致性檢測的情況下,直接運用語言算術平均算子對供應商的所有語言決策信息進行融合。相反,本文提出的模型首先對原始給定的語言偏好關系的一致性進行檢測和改進,然后計算供應商的排序權重向量和決策結果。因此,本文提出的語言決策模型相較于文獻[30]中的決策方法更為有效。 針對決策信息為語言變量的決策問題,本文首先研究構造乘性一致語言偏好關系的方法,為了盡可能保留原始決策信息,引入局部調整策略,設計了一種乘性一致性改進算法,使得改進后的語言偏好關系具有滿意乘性一致性,并證明算法的收斂性。隨后,基于DEA模型建立了最優化模型,進而確定方案的排序權重向量。最后,構建一個基于一致性局部調整策略和DEA方法的語言決策模型,從而得到合理可靠的決策結果。 本文僅考慮了決策過程中專家提供的決策信息完全可知的情況,針對專家因某些因素而沒有給出決策信息的情況,即如何針對不完全語言偏好關系構建合理有效的決策模型尚有待進一步研究。同時,在語言偏好決策模型的構建過程中運用傳統自評優先DEA模型只能分辨出決策單元是DEA有效還是非有效的,可能導致不具備對決策單元(決策方案)進行排序的能力,因此如何運用交叉效率DEA模型來克服傳統自評優先DEA模型的不足,設計基于交叉效率DEA模型的語言偏好決策方法可以作為今后的研究方向。
3 語言偏好關系的一致性局部調整算法
3.1 乘性一致語言偏好關系的構造
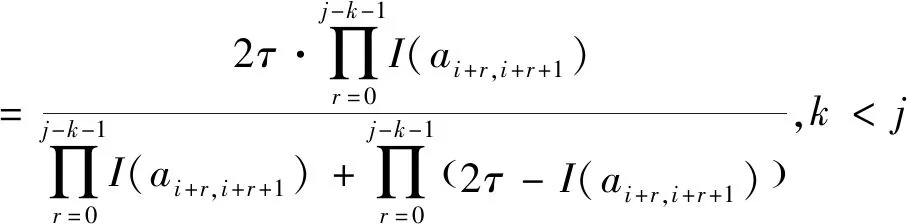
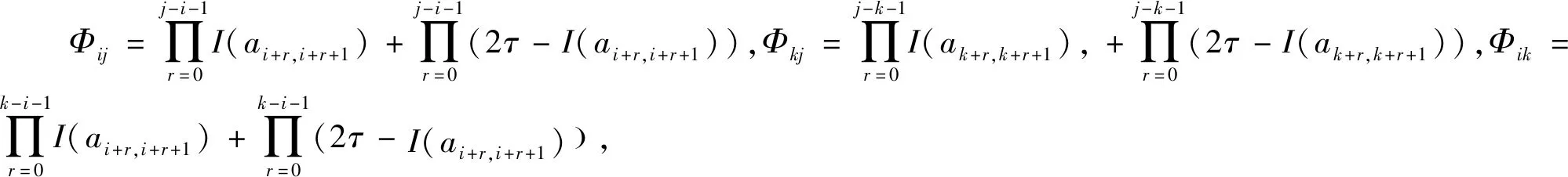
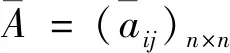
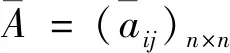
3.2 基于局部調整策略的一致性改進算法
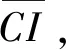
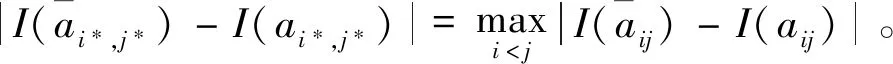
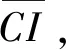
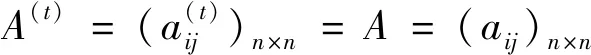
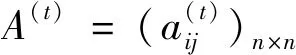
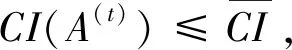
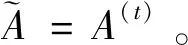
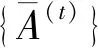
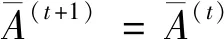
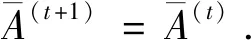
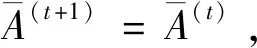
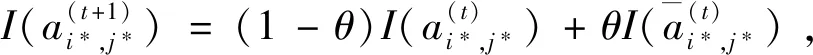
4 語言決策模型
4.1 基于DEA的排序權重確定方法

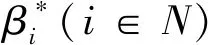
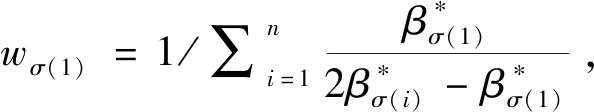
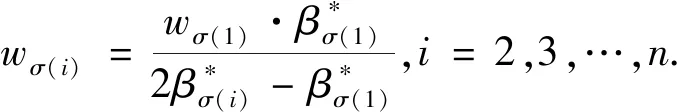
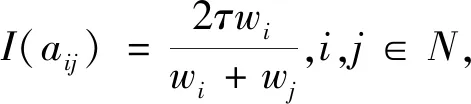
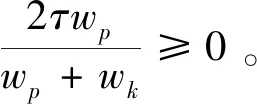
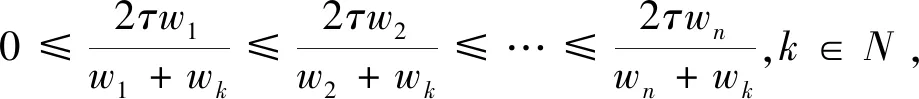
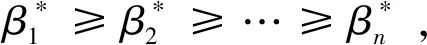
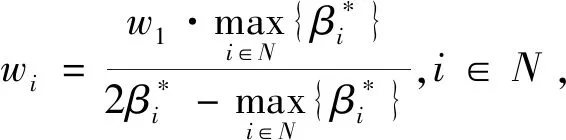
4.2 語言決策模型
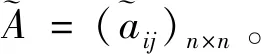
5 數值實驗與對比分析
5.1 數值實驗
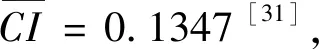
5.2 對比分析
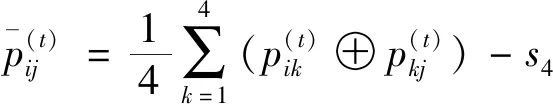
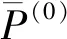
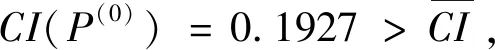
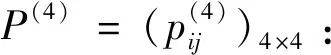
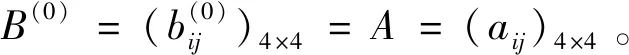
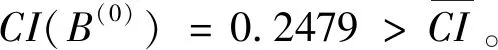
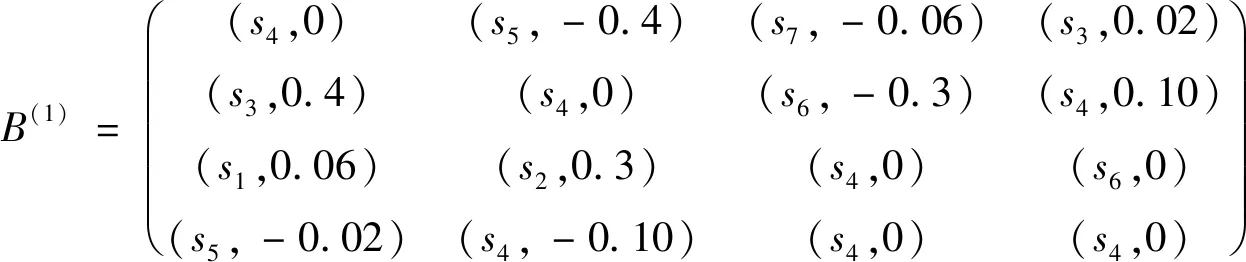
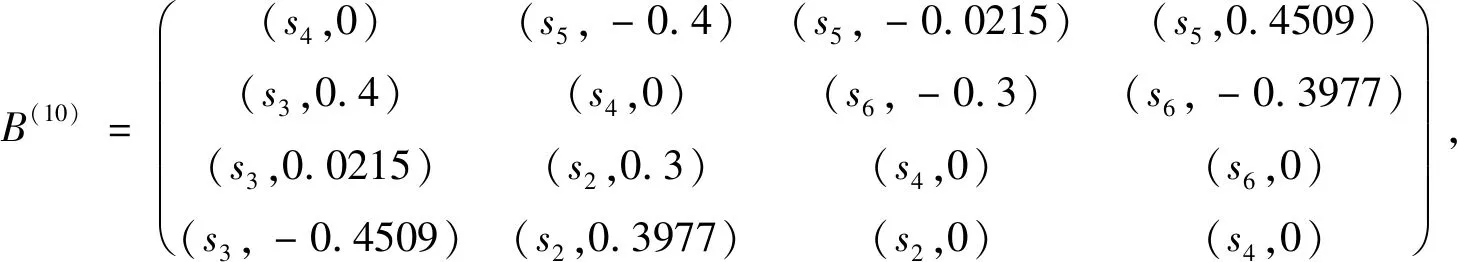
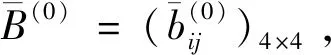
6 結語

