基于等光頻細分重采樣的調頻干涉測距方法

包為政，張福民，曲興華

(天津大學 精密測試技術及儀器國家重點實驗室，天津 300072)

引 言

調頻連續波(frequency modulated continuous wave,FMCW)激光雷達具有大帶寬、高精度、高測量分辨力等優點，廣泛應用于各種非接觸式測量領域[1-2]。其基本原理是對發射激光的頻率進行線性調制，本振信號與回波信號干涉形成拍頻信號，通過提取拍頻信號中的頻率信息來計算測量距離[3]。實際測量時，激光器存在調制非線性問題，造成測量信號頻譜展寬嚴重，使得調頻連續波測距系統的測距精度受到很大限制[4-6]。

為解決這一問題，學者們提出了很多有效的方法，主要有主動補償與后處理兩大類技術。主動補償主要有預校正補償及反饋調頻技術、電光鎖相環反饋校正技術等[7-8]。后處理技術有分子頻率參考校正、光頻梳校正、雙光路校正等方法[9-11]。其中雙光路校正技術結構簡單、裝置易于搭建，常用方法為雙光路零點重采樣法，該方法有兩路干涉光路，而輔助干涉光路產生的拍頻信號也包含有非線性信息，提取輔助干涉光路的拍頻信號零點位置點對測量光路拍頻信號對應位置點進行采樣處理，以達到消除非線性的目的。但是在利用雙干涉光路進行采樣的過程中，為了滿足奈奎斯特采樣定律，需要保證時鐘信號頻率至少為被采樣信號的兩倍，這是這種方法的缺陷，因為要保證輔助干涉光路的光程差至少要大于兩倍的測量距離。進行大長度測量時，所需輔助干涉光路的參考延時光纖將會更長，受環境振動以及光纖色散等問題的影響將會越來越大，需要嚴格控制參考光纖的溫度、濕度、偏振態以及進行色散補償。哈爾濱工業大學的XU等人研究了振動、色散等因素對于調頻連續波測距的影響，并基于希爾伯特變換對信號進行移相來增加測量受限距離[12-14]。天津大學PAN等人分析了色散對于等光頻重采樣測距精度的影響并對色散進行了校正，還研究了多重信號特性算法用于估計均方根誤差，并提出了精度評定方法[15-17]。日本金澤大學的IIYAMA等人提出了利用電子鎖相環對輔助干涉光路拍頻信號進行倍頻的方法，對輔助拍頻信號倍頻后，可以利用短的參考延時光路對長距離測量信號進行重采樣解決非線性問題，但是這種方法加入了倍頻系統，使得測量分辨力與精度也會受到倍頻精度的影響，引入了額外的誤差，大大增加了系統成本與復雜度[18]。

本文中在雙光路校正技術的基礎上，提出了等光頻細分重采樣法來消除激光器調制非線性的影響，對等光頻細分重采樣算法進行了詳細的推導，通過仿真驗證了公式的正確性，結合算法搭建相應短光纖輔助測距光路進行等光頻細分重采樣系統測距能力的實驗驗證，實現了利用短光纖對長距離測量信號重采樣。

1 基本原理

等光頻細分重采樣系統的測量原理及光路結構如圖1所示。系統采用雙光路結構，由兩路并聯的馬赫-曾德爾干涉光路組成，一路為作為測量干涉光路，另外一路作為輔助干涉光路。

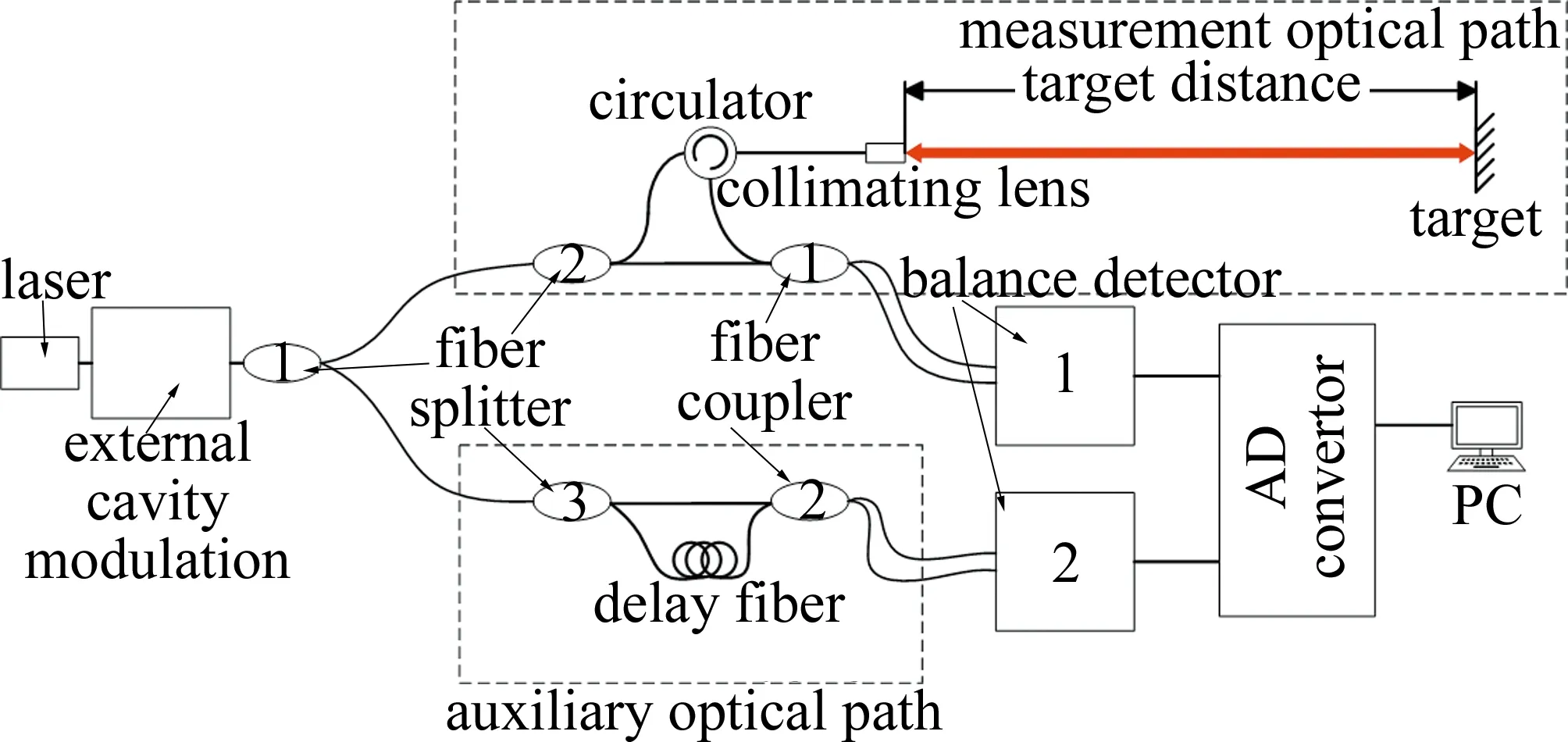
Fig.1 Optical structure diagram of laser ranging system of equal optical frequency subdivision resampling

系統主要由光纖光路構成，光纖采用單模光纖，激光通過第1個80∶20光纖分束器1后分為兩束光，能量較高一束進入測量干涉光路部分，保證探測回波信號能量足夠與本振信號形成信噪比較高的拍頻信號；另一束進入輔助干涉光路部分。進入測量干涉光路部分的光再經過分束器2分為出射測量光與本振光，出射測量光通過光纖環形器及準直透鏡發射向待測目標鏡，反射回光通過環形器再與測量干涉光路本振光在耦合器1處發生干涉；另一束進入輔助干涉光路部分經過分束器3分為兩束，一路經過已知長度的短參考光纖后與另一路輔助干涉光路本振光發生干涉。

激光器發出的掃頻激光電場強度可以表示為：

E(t)=A(t)cos(ωt-φ0)

(1)

式中,A(t)表示電場振幅隨時間變化值，由于激光器頻率調制的過程中伴隨有非自主的幅度調制，所以激光電場振幅大小是隨時間不斷變化的，但是對相位計算并不影響，故可看作恒定值A0，ω為調頻激光器出射激光的電場角頻率，φ0為初始相位。

由歐拉公式可以得到出射激光電場強度指數形式的表達式為：

E(t)=A0eiφ(t)

(2)

式中,φ(t)為瞬時相位，為掃頻激光器出射激光瞬時角頻率ω(t)在時間t的積分：

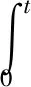
(3)

掃頻激光器出射激光瞬時角頻率為：

ω(t)=Ωt+ω0

(4)

式中,ω0為掃頻初始角頻率，Ω為激光器掃頻角頻率的變化率，理論上Ω=4πB0/T，其中B0為掃頻帶寬，T為掃頻周期，實際中掃頻角頻率變化率不是固定不變的，導致了掃頻非線性問題。

將(3)式、(4)式代入(2)式得：

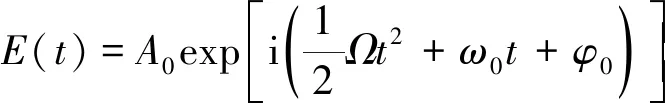
(5)

掃頻激光器出射激光分為兩路,分別進入輔助干涉光路部分與測量干涉光路部分，進入輔助干涉光路部分激光由分束器3分為兩束分別進入輔助干涉光路倆臂，由于輔助干涉光路兩臂之間存在光程差，導致兩路激光在耦合器2處存在時間延遲，在耦合器2處輔助干涉光路測量臂及參考臂對應的電場強度分別為：

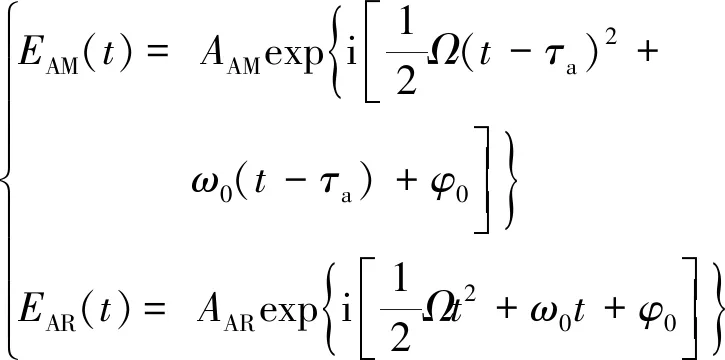
(6)

式中,τa為輔助干涉光路兩臂時間延遲，AAM為輔助干涉光路測量臂信號幅值，AAR為輔助干涉光路參考臂信號幅值。

輔助干涉光路兩臂信號在探測器2處疊加電場光強變化為電場復振幅與共軛的乘積：

Ia(τ,t)=(EAR+EAM)·(EAR*+EAM*)

(7)

由于探測器無法探測到疊加高頻信息，探測器2處僅探測到光強拍頻信號，可以表示為：

Ia(τa,t)=IAR+IAM+

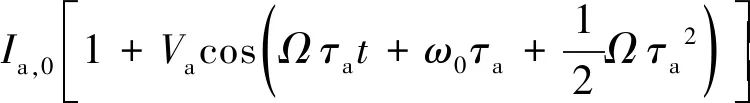
(8)

式中,IAR為輔助干涉光路參考臂信號光強，IAM為輔助干涉光路測量臂信號光強，φAR(t)為輔助干涉光路參考臂瞬時相位，φAM(t)為輔助干涉光路測量臂瞬時相位，Ia,0為輔助干涉光路平均光強，Va表示輔助干涉光路光電探測器表面幅值。公式中最后一項為光程差時延對應的2階小量，由于等光頻細分重采樣法所需的輔助光路光程很短，所以此項可以忽略不計，輔助拍頻信號公式即可表示為：

Ia(τa,t)=Ia,0[1+Vacos(Ωτat+ω0τa)]

(9)

如圖2所示，首先提取輔助干涉光路產生的拍頻信號峰谷值點作為特征點，特征點攜帶有不斷變化的非線性信息。

峰值特征點A點拍頻相位為：

φA=ΩAτatA+ω0τa=2πm

(10)

谷值特征點B點拍頻相位為：

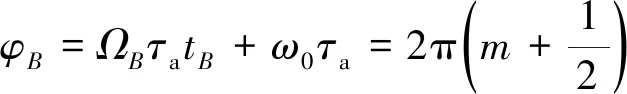
(11)

式中,φA,φB分別為A,B兩點的瞬時相位;tA,tB分別為

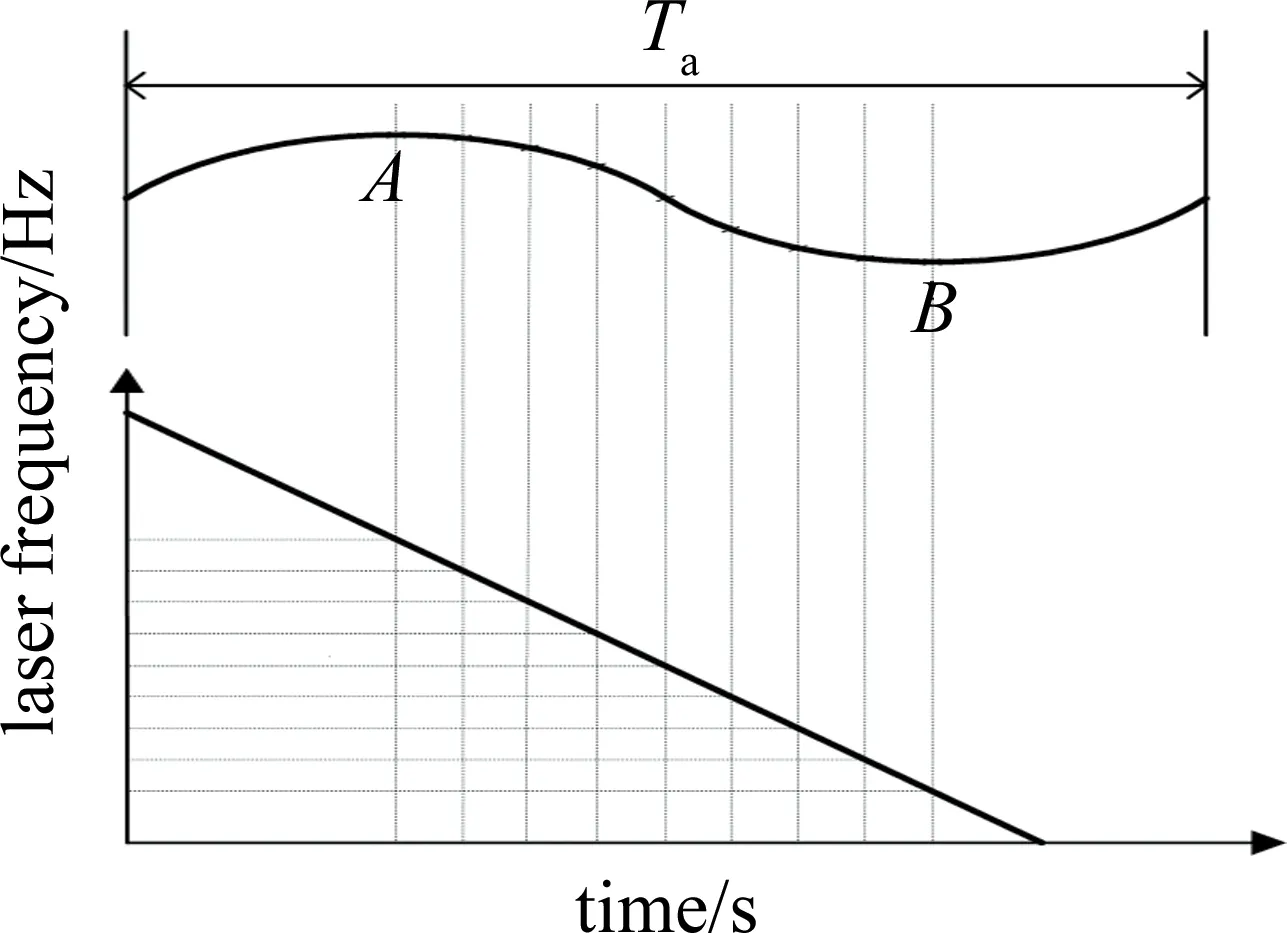
Fig.2 Schematic diagram of equal optical frequency subdivision of auxiliary beat signal

A,B兩點對應的實際時間;ΩA,ΩB為A,B兩點對應的實時角頻率變化率;m表示峰谷值特征點A,B在輔助拍頻信號的第m個周期。

所以A,B兩點之間的拍頻相位差為：

ΔφA,B=φB-φA=π

(12)

對應的A,B兩點之間的激光角頻率差為：

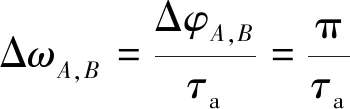
(13)

將輔助拍頻信號特征點之間的半個拍頻周期細化為N段等時間間隔段，兩相鄰間隔點之間的時間間隔即為Ta/(2N)，Ta為一個輔助拍頻信號的周期長度。在相鄰特征點之間，掃頻頻率非線性變化對輔助干涉光路拍頻信號影響很小，特征點之間掃頻頻率變化具有局部線性，特征點之間的半個周期內等時間間隔點對應的等光頻間隔點，結合(13)式可得相鄰間隔點之間的對應激光角頻率差為：

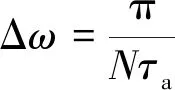
(14)

由于輔助干涉光路光程差長度不變，τa為恒定值，所以輔助拍頻信號間隔點之間對應的激光角頻率間隔恒為π/(Nτa)。

測量干涉光路拍頻信號表達式與輔助干涉光路拍頻信號表達式推導過程相同，測量拍頻信號Im可以表示為：

Im(τm,t)=Im,0[1+Vmcos(Ωτmt+ω0τm)]

(15)

式中,Im,0為測量干涉光路平均光強，Vm表示測量干涉光路光電探測器表面幅值，τm為測量干涉光路兩臂時間延遲。

利用等光頻細分后的輔助拍頻信號點作為時鐘信號采樣測量拍頻信號，使得重采樣后的測量拍頻信號點之間同樣滿足等光頻間隔關系，重采樣后的測量信號將不再以時間間隔而以光頻間隔π/(Nτa)為基本單位，將原有的等時間間隔采樣轉化為等頻率間隔采樣，進行等光頻細分重采樣后的測量拍頻信號Im可以表示為：

(k=0,1,2,…)

(16)

對等光頻細分重采樣后的測量拍頻信號進行快速傅里葉變換(fast Fourier transform,FFT)[19]得到測量干涉光路兩臂時間延遲：

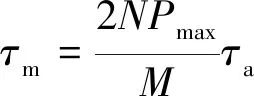
(17)

式中,Pmax為FFT頻譜的峰值位置，M為總FFT點數。

可以得到測量距離公式為：

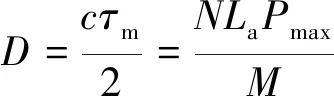
(18)

式中,c為光速，La為輔助干涉光路兩臂之間的光程差。

等光頻細分重采樣系統允許測得的最大范圍與細分段數N成正比：

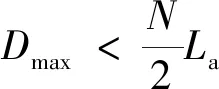
(19)

由(19)式可知，等光頻細分重采樣系統可以通過增多細分段數N的方式減少所需輔助干涉光路光程差La的長度，所以等光頻細分重采樣系統可使用較短的輔助參考光纖,代替原有雙光路零點重采樣系統所必需的長參考光纖，理論上細分段數的上限值受到原始數據采集頻率的限制，須保證細分后間隔點不重疊。

2 實驗與結果

2.1 等光頻細分重采樣公式仿真驗證

為驗證重新推導得出的等光頻細分重采樣頻譜分析公式的正確性，在這里以多項式信號作為調頻非線性拍頻信號的主要形式進行仿真驗證。

設掃頻激光器調制范圍為1543.7nm～1553.7nm，掃頻速度預設為100nm/s,則激光器調制頻率變化率為：

Ω=12508095395690×[1+0.001×sin(2000π×t)]

(20)

式中，0.001×sin(2000π×t)項為調制頻率變化率非線性波動干擾項，實際波動范圍以及頻率要小于此，為驗證等光頻細分重采樣法的處理能力，將波動范圍及波動頻率增大。

預設測量距離為9m，輔助干涉光路光程差為5m，測量距離大于輔助干涉光路光程差的1/2，輔助拍頻信號可以表示為：

Sa=6×cos(2π×Ω×t×5/c+193087468623286×5/c)

(21)

測量拍頻信號可以表示為：

Sm=8×cos(2π×Ω×t×18/c+193087468623286×18/c)

(22)

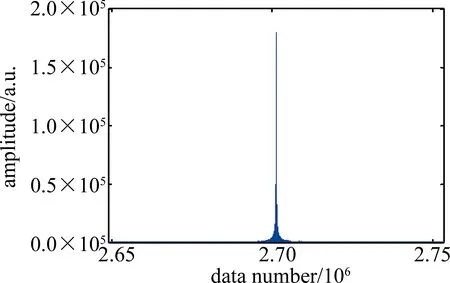
Fig.3 Spectral diagram of the simulated signal after equal optical frequency subdivision resampling

仿真結果如圖3所示。采樣點數設置為90萬個點，采樣頻率為25MHz，用輔助拍頻信號Sa對測量拍頻信號Sm進行等光頻細分重采樣后，進行100倍補零FFT運算，得到FFT頻譜的峰值位置點為2701306，總FFT點數為6002900，等光頻細化段數N為4段，保證理論允許的最大測量范圍大于實際范圍，代入(16)式得到仿真距離：

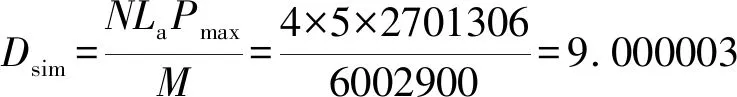
(23)

求得仿真距離為9.000003m，由于離散化誤差的影響，造成結果存在細微偏差。

2.2 實驗驗證等光頻細分重采樣系統測距能力

為驗證等光頻細分重采樣系統測距能力以及對調制非線性的消除效果，按照圖1系統搭建了實驗裝置,如圖4所示。實驗中使用的是Luna PHOENIX 1400可調諧激光器，調制范圍設置為1540nm～1560nm，調制速度為100nm/s；測量光路從準直透鏡出射到空間測量光路之前存在固有光纖光路長度3.2m；輔助干涉光纖長度為2.104m，輔助干涉光路長度小于測量距離的2倍；待測目標鏡放置于帶有激光干涉儀(Re-nishawXL-80)的1m長導軌上，由近到遠移動目標鏡的位置，移動步長為100mm；示波器采樣頻率為25MHz，使用設計的等光頻細分重采樣測距系統對目標鏡的距離進行測量。

如圖5所示，其中實線部分為等光頻細分重采樣系統輔助干涉光路產生的輔助拍頻信號，其中圓形點表示等光頻細分處理輔助拍頻信號后得到的等光頻間隔時鐘信號點位置，細分段數N=8，虛線部分為測量拍頻信號，其中叉狀點表示等光頻間隔時鐘信號點對測量信號重采樣后的位置點。由于輔助干涉光路光程長度小于測量光路光程長度，造成參考信號頻率小于測量信號頻率。如果直接對短距離參考光路輔助干涉光路拍頻信號提取零點位置對測量信號進行重采樣，將使重采樣后的信號嚴重失真，使用等光頻細分重采樣算法后，輔助拍頻信號每個周期的可用重采樣時鐘信號點數增加，使得重采樣過程可以滿足奈奎斯特采樣定理。

Fig.4 Experimental device diagram

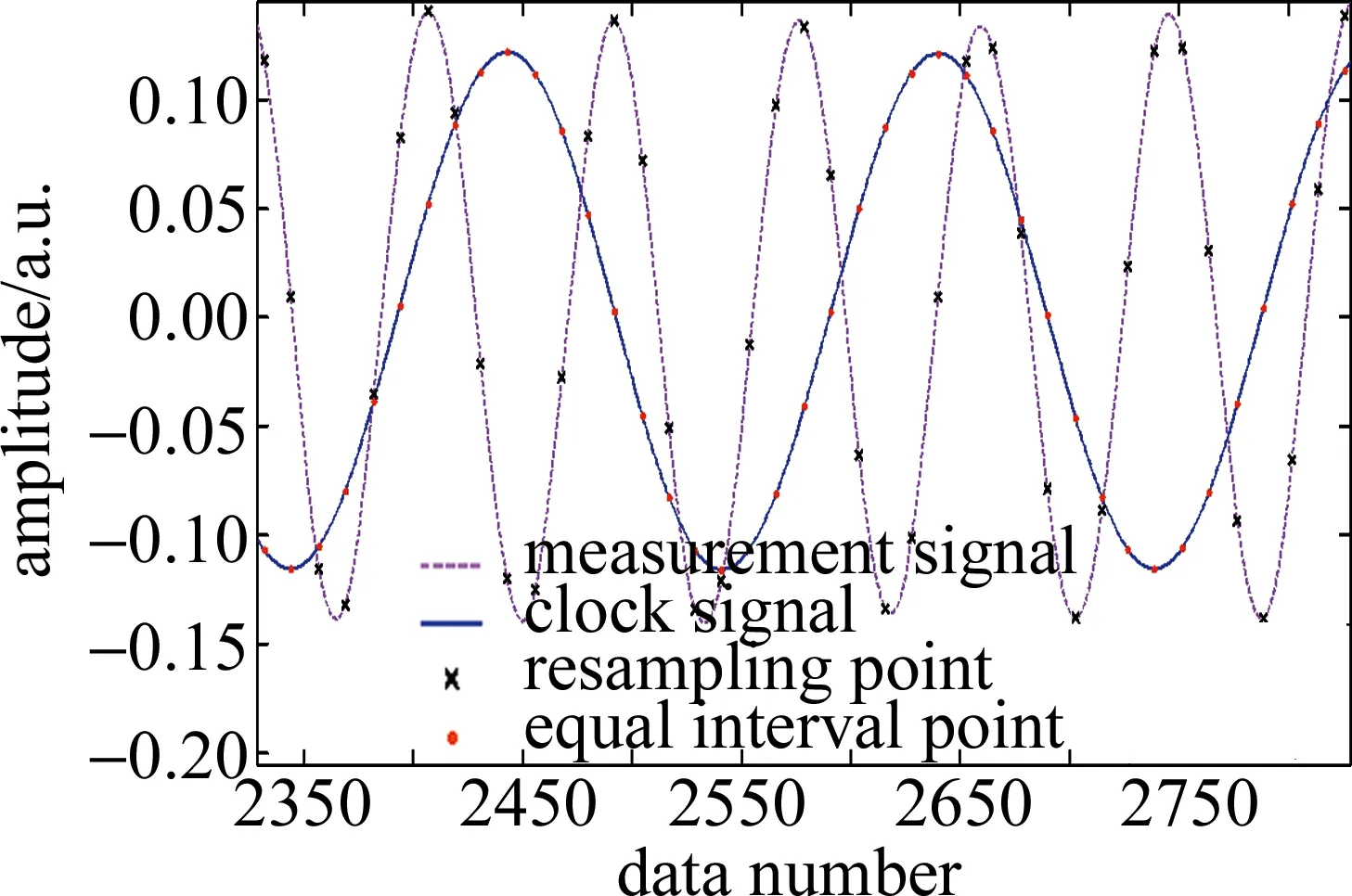
Fig.5 Comparison of clock signal and measurement signal waveforms of equal optical frequency subdivision resampling system

對比圖6兩小圖可以看出，圖6a中,由于激光器調制非線性的影響，對測量拍頻信號直接進行FFT后的頻譜發生了嚴重展寬，無法識別出準確的距離信息，測量分辨力也極大地下降；圖6b中，經過等光頻細分重采樣后的測量信號頻譜可以準確地識別出測量信號中的距離信息，半峰全寬接近理論分辨力的大小，證明了等光頻細分重采樣有效地抑制了激光器的調制非線性的影響。

如圖7所示，在實驗室環境下，在絕對距離4.3m(其中包含固有光纖光路長度)測量范圍內，等光頻細分重采樣測距系統測量值與激光干涉儀距離變化值相比最大殘余誤差小于±18.46μm，最大標準差為22.23μm。此誤差主要來源于如下幾個方面：測量光路信號本身存在環境振動的影響，如位移臺的抖動，光學支撐器件的振動放大以及測量光路光纖光路部分存在的環境振動，細微振動造成的多普勒頻移導致傅里葉變換后的頻譜發生展寬和漂移使得測量精度降低；激光干涉儀本身也存在測量標準差；等光頻細分重采樣測距系統與激光干涉儀出射光并不能完全在一條直線上，存在一定夾角造成阿貝誤差。

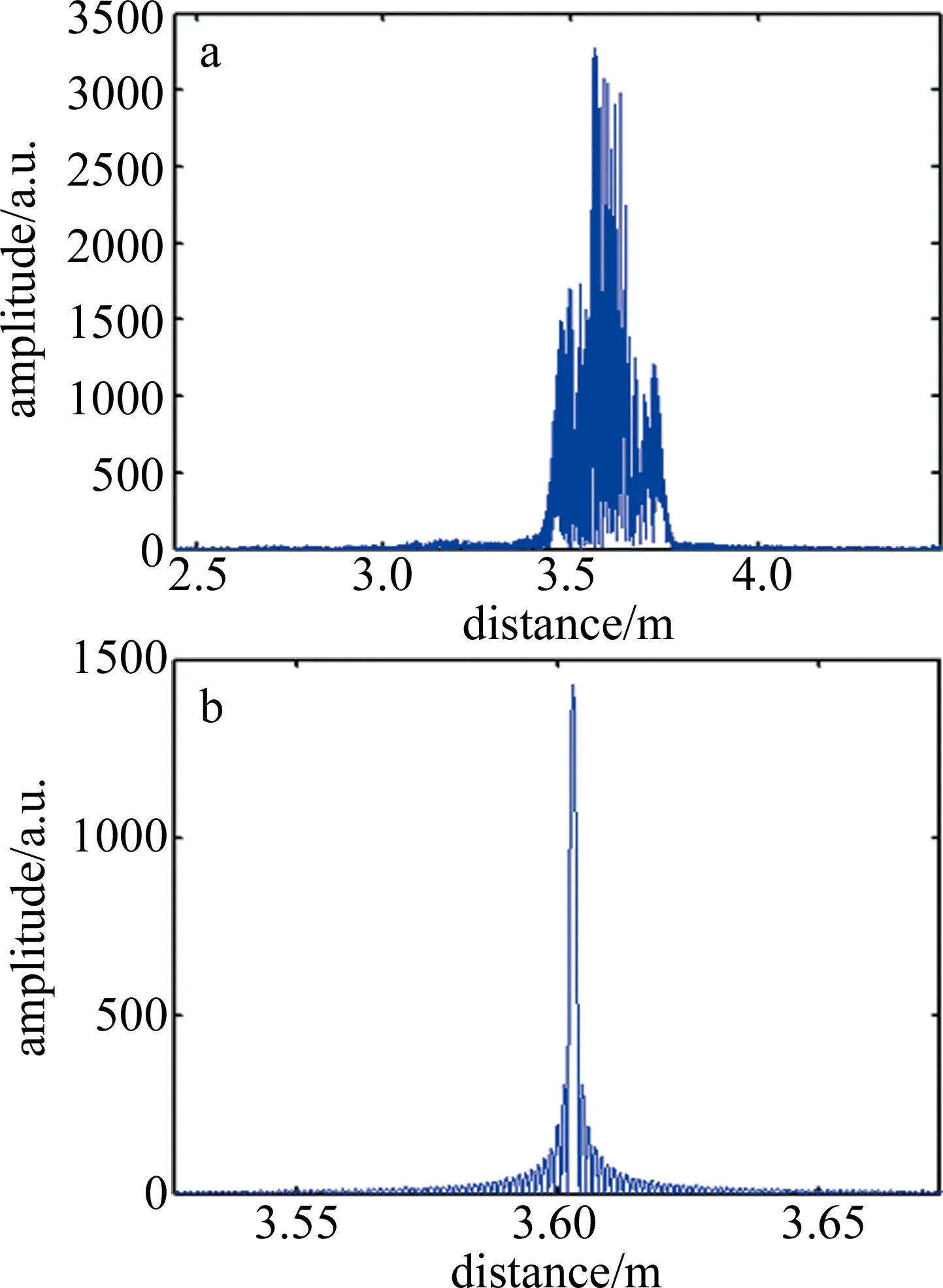
Fig.6 Comparison of nonlinear cancellation effects of the measured beat signal

a—before equal optical frequency subdivision resampling b—after equal optical frequency subdivision resampling

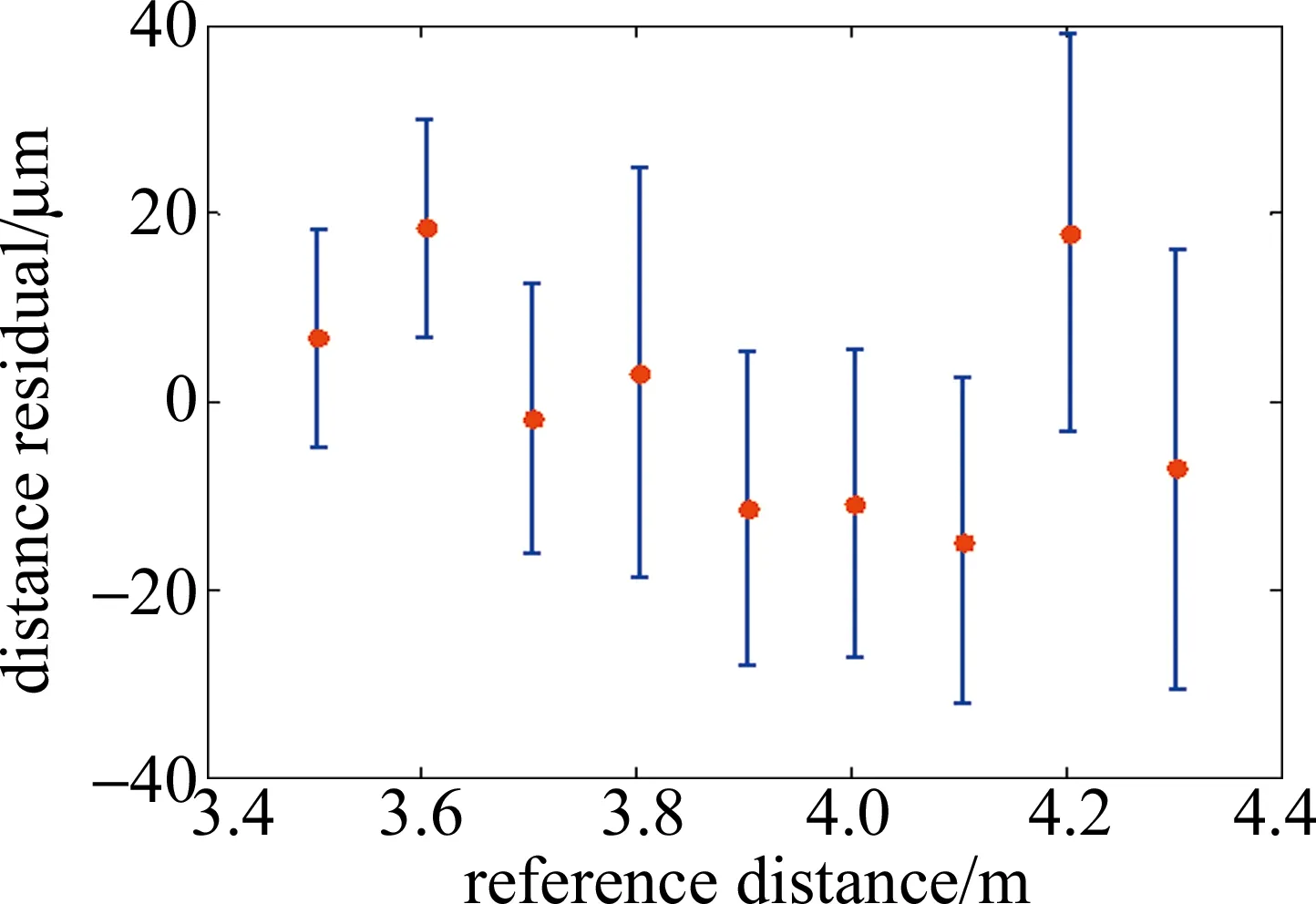
Fig.7 Distance residuals compared with laser interferometer within 4.3m

3 結 論

在雙光路校正技術的基礎上提出了等光頻細分重采樣法，并對此方法進行了詳細的推導，該方法可以通過對特征峰谷值點之間信號段進行等光頻細分，以增加輔助干涉拍頻信號時鐘信號點的提取數量，消除調制非線性的同時，降低了對輔助光路長度的要求。實驗結果表明：等光頻細分重采樣系統在100nm/s的調節速度以及20nm的帶寬時，對4.3m測量范圍的待測目標鏡進行測量，使用等光頻細分重采樣法對信號進行處理后，測量結果與激光干涉儀相比的最大殘余誤差在±18.46μm之間，最大測量標準差為22.23μm。實驗結果驗證了本文中理論分析的可行性，等光頻細分重采樣的方法有效地抑制了激光器的調制非線性的影響。通過多個位置處的重復測距實驗表明，該方法有較高的單點穩定性與測距準確度。