基于優化EEMD和支持向量機的國內大豆價格預測

楊 靜，張大斌，方潔鳳，李培漢

（華南農業大學數學與信息學院，廣東 廣州 510642）

【研究意義】大豆是土地密集型農產品，單產較低，既是重要的糧食作物，也是油料的重要來源，在國民經濟中占有重要地位。大豆價格的穩定是大豆市場健康發展的重要前提和保障，但我國人均耕地面積較少，大豆主要依靠進口，易受到國際政治經濟、國家宏觀政策等因素的影響。因此，了解當前市場價格變化情況并對大豆價格建立有效的預測模型，洞悉未來市場價格的變化趨勢，有助于規避風險，對促進大豆市場健康發展具有重要的實際意義。【前人研究進展】目前在大豆價格的研究領域多采用單一模型，如徐鑫洲等[1]基于系統動力學的我國大豆價格預測分析，朱婧等[2]基于改進GM]1,1）模型的中國大豆價格預測。這類單一預測模型對時間序列的波動特征要求較高，對于具有非線性、非平穩特點的大豆時間序列來說，其預測精度有待進一步提高。經驗模態分解（Empirical Mode Decomposition,EMD）是Huang等[3]于1998年提出的一種新型自適應信號時頻處理方法。與傅里葉分解、小波分解等方法不同，EMD方法是依據信號自身的時間尺度特征來進行信號分解，無需預先選擇任何基函數，在處理非平穩及非線性信號上，具有非常明顯的優勢。國內一些學者已經將EMD運用于預測領域，如葉林等[4]基于經驗模態分解和支持向量機的短期風電功率組合預測模型，王文波等[5]基于EMD與神經網絡的中國股票市場預測，蔣軼軍等[6]基于EEMD和進化KPCR的復雜時間序列自適應預測模型，均取得了良好的預測效果。上述分解集成的思想，能有效解決單一預測模型的不足。【本研究切入點】基于這種思想，本研究考慮大豆時間序列在實際分解過程中存在模態混淆和端點效應問題，對EMD分解方法進行了改進，在分量預測模型SVR的建立過程中，通過遺傳算法實現模型參數的優化選擇。【擬解決的關鍵問題】將不同分量的預測結果集成，實現準確預測，對于指導大豆的生產和進出口貿易具有較高的指導意義。

1 材料與方法

1.1 EEMD分解優化

1.1.1 集成經驗模態分解 EMD方法本質上是對信號進行平穩化處理，將信號中真實存在的不同尺度波動或趨勢逐級分解出來，產生一系列具有不同特征尺度的數據序列，每一個序列成為一個本征模態函數（Intrinsic Mode Function，IMF）。最低頻率的IMF分量稱為殘余項，代表了原始信號的趨勢或均值，分解得到的各個IMF突出了數據的局部特征并具有明顯的物理意義。

為了改善EMD中存在的模態混疊現象，Wu等[7]進一步提出了EEMD方法。該方法是一種新的噪聲輔助數據分析方法，其核心思想是認為每個觀察到的數據都融合了實際的時間序列信息和噪聲，因此即使同一過程數據被不同的人收集得到，也具有不同的噪聲水平，但是其整體均值接近于真實的時間序列。為解析出數據的真實信號，將多組具有有限振幅的白噪聲序列添加到原始序列上，然后分別進行分解，將相應分量的均值作為真實分量。EEMD方法的步驟如下：

（1）將正態分布的白噪聲n(t)加到原始信號X(t)，計算新的信號：

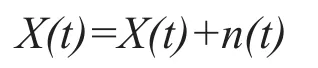
（2）將新的信號X(t)進行EMD分解，得到各分量imfi(t)和殘余項r(t)。

（3）重復N次步驟（1）和（2），每次加入不同的正態分布白噪聲序列：

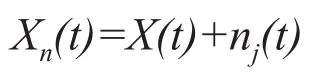
（4）將每次得到的imf分量和殘余項r(t)做集成平均處理后作為最終結果：

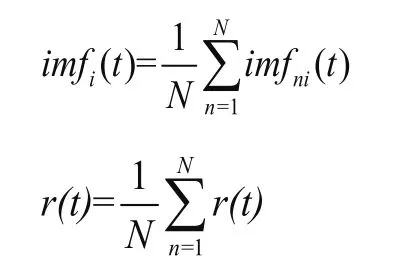
1.1.2 平行延拓法 端點效應是Hung等[3]在研究EMD的篩分過程時發現的，指的是在EMD分解中反復運用3次樣條方法根據極值點對上、下包絡進行插值，但信號的端點不可能同時是極大值點或極小值點，因此得到的包絡曲線會在兩側的端點附近出現幅值發散的現象，隨著篩分過程的不斷進行，發散現象逐漸傳播至內，使分解結果嚴重失真，產生假頻信號。

平行延拓法是一種基于極值點的延拓方法，它通過利用端點附近的兩個相鄰極值點（一個極大值、一個極小值）處斜率相等這一特性，來獲取被分析的有限信號序列左、右兩端的延拓極值點，可以有效解決EMD中的端點效應問題[8]。

假設被分析信號序列{(t(n),Z(n))|n=1,2,…,}，其極大值信號序列為{ (tm(i),Z(i))|i=1,2,…,Nmax}，極小值信號序列為 {(tn(i),V(i))|i=1 ,2,…,Nmin}，并假設信號序列的起始極值點為1個極小值點，信號序列最末端的極值點為極大值點，平行延拓法的計算步驟如下：

（1）把起始端點作為起始延拓的極大值點，獲取極大值點值為：

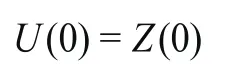
（2）獲得起始端點相鄰極值點連線的斜率：

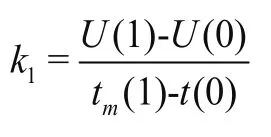
（3）求取起始延拓的極小值點值為：

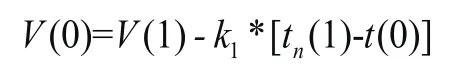
（4）求取起始延拓的極值點橫坐標為：

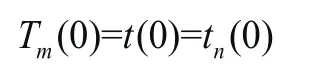
（5）與被分析信號的起始端相同，把終止端點作為末端延拓的極小值點，獲取極小值點值為：

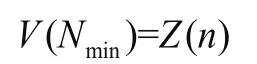
（6）獲得信號序列終止端點的相鄰極值連線的斜率：

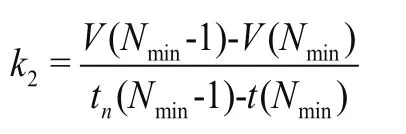
（7）求取末端延拓的極大值點值為：

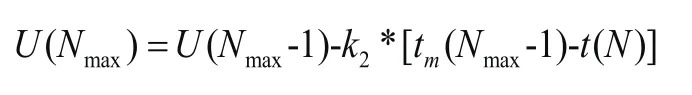
（8）求取末端延拓的極值點橫坐標：

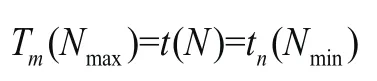
通過平行延拓方法在原始時間序列兩端延拓出極大值和極小值，避免了直接將端點作為極值點進行分解的魯棒性，可以抑制端點效應帶來的問題，有效改善原始EMD方法的分解效果。

1.2 基于改進的EEMD和SVR的預測建模

以上述理論為基礎，我們提出一種優化模型，對EMD模型進行優化分解，得到最佳的分解分量，以實現更精確的預測結果。基于改進的EEMD和支持向量回歸的預測建模過程如圖1所示，對于給定的時間序列數據，預測建模過程的具體實現步驟如下[9-10]：

（1）以原始時間序列為對象，加入白噪聲序列，得到新的序列X(t)。

（2）對新的時間序列X(t)進行端點處理，采用平行延拓法對序列兩端延拓，重構出極大值和極小值，再對延拓后的序列X(t)*進行EMD分解，得到多個模式分量imfi(t)。

（3）重復步驟（1）和（2），但是添加不同的白噪聲，將每次得到的多個模式分量和殘余項相應進行集成平均作為最終的分量和殘余項r*(t)。

（4）對每個分量建立SVR模型，采用遺傳算法對模型參數進行優化，得到不同分量模型相應的參數，進而得到不同分量的最佳的序列預測模型：

（5）在各個分量預測結果的基礎上，集成得到最終的時間序列預測值Y(t)：

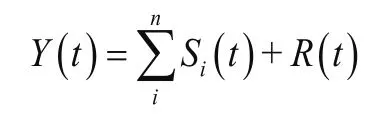
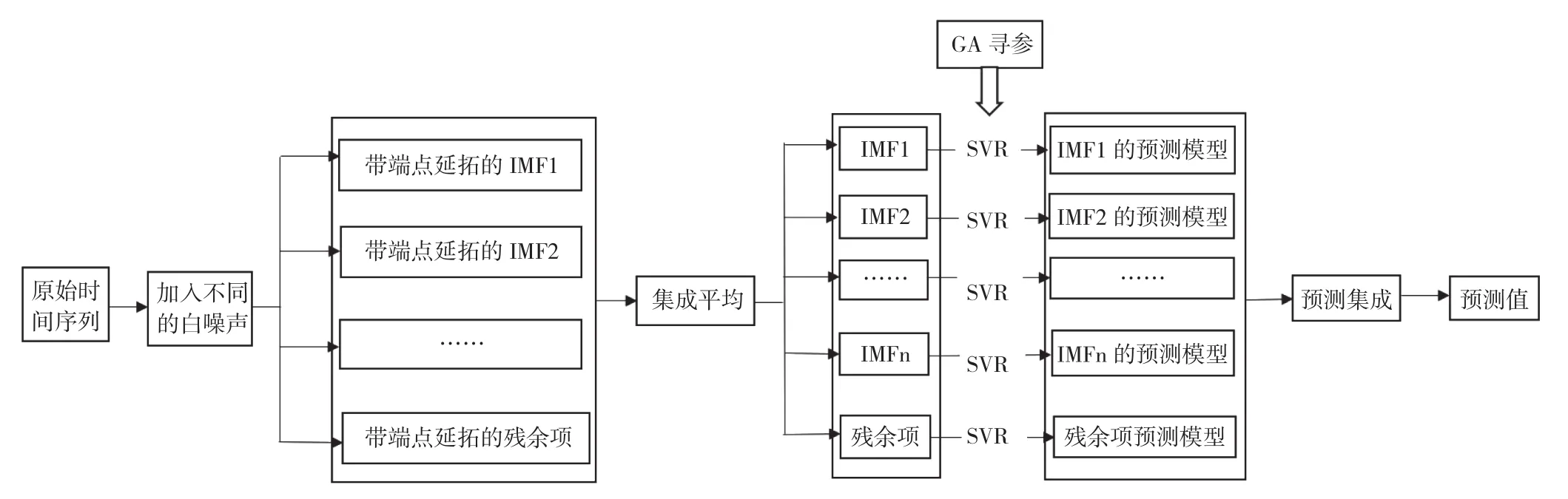
圖1 基于改進的EEMD和支持向量回歸（SVR）的建模過程Fig.1 Modeling process based on improved EEMD and support vector regression (SVR)

1.3 數據獲取

選用中國集貿市場大豆—中等月度價格展開研究。以2000年1月至2018年10月共226個月度價格數據為數據集，選取2000年1月至2015年1月共181個數據作為訓練集，2015年2月—2018年10月共45個數據作為測試集，具體數據均來源于中國經濟與社會發展統計數據庫（圖2）。

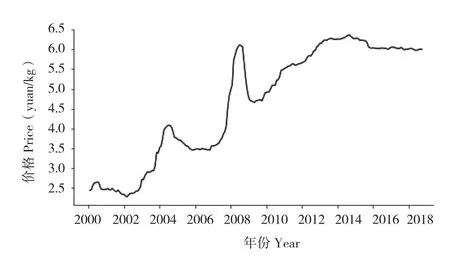
圖2 全國集貿市場大豆價格（元/kg）Fig.2 Soybean prices in Chinese market（yuan/kg）

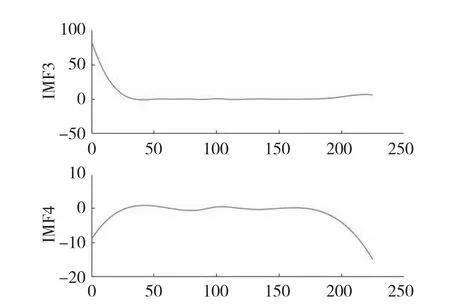
圖3 EMD分解IMF3和IMF4Fig.3 IMF3 and IMF4 decomposed by EMD

2 結果與分析

2.1 價格序列分解與分析

為驗證平行延拓端點處理方法的優化效果，采用EMD分別對中國集貿市場大豆—中等月度價格序列進行分解，得到的IMF3和IMF4分量如圖3所示；對中國集貿市場大豆—中等月度價格序列平行延拓后再進行EMD分解，得到的IMF3和IMF4分量如圖4所示。對比圖3和圖4可以看出，原始EMD分解的序列體現出明顯的端點效應，而該現象經過平行延拓法處理后可以得到有效抑制。

采用EEMD分解中國集貿市場大豆—中等月度價格序列，設置Nstd=0.01，NE=100，較好的解決了模態混疊的問題，得到的分量圖和頻譜圖如圖5和圖6所示。通過改進分解方法得到5個分量和殘余項，從頻譜圖可看出經過該優化模型分解得出的IMF分量沒有明顯的模態混疊現象。其中，IMF1～IMF3頻率較高，代表短期內不平衡的現象，該現象發生頻繁，但影響時長小；IMF4和IMF5分量頻率較低，代表大豆價格短期內重大事件對市場價格的影響[11]，影響時長相對較大；殘余項則代表大豆價格長期的發展趨勢，和國家的經濟發展趨勢一致，穩步上升。

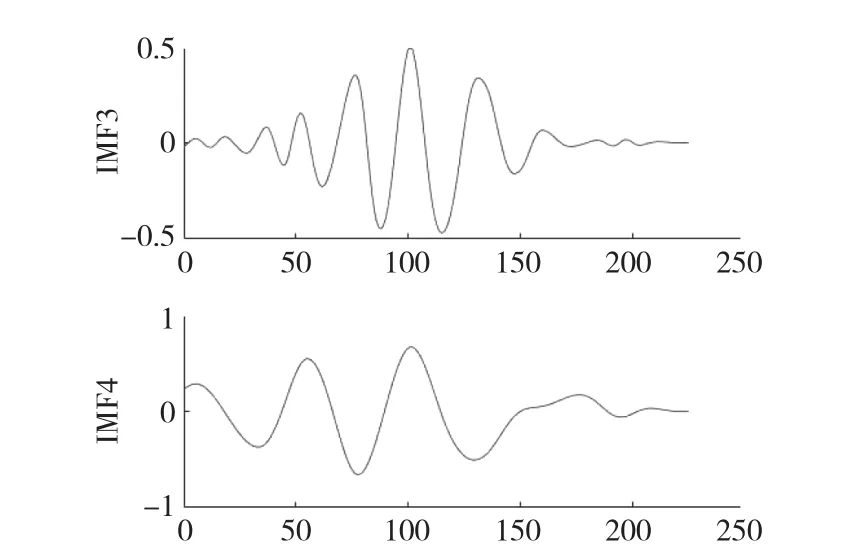
圖4 平行延拓IMF3和IMF4分量Fig.4 Parallel extension components-IMF3 and IMF4

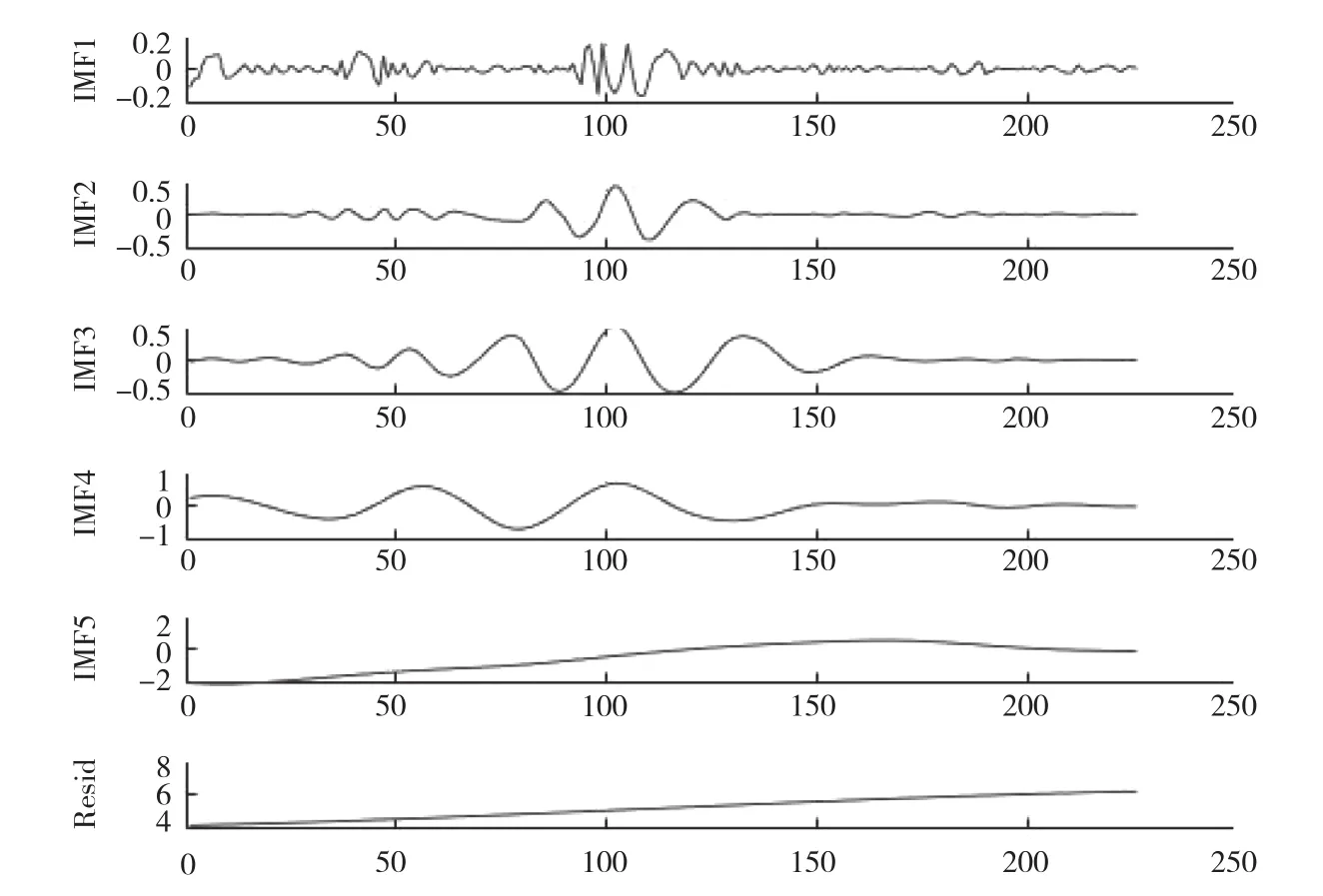
圖5 EEMD和平行延拓優化的價格序列分解Fig.5 Price sequence decomposition of EEMD and parallel extension optimization

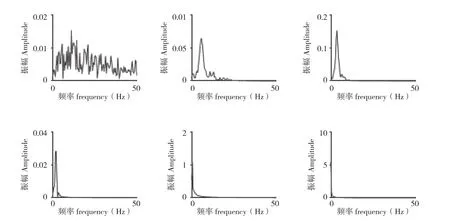
圖6 EEMD和平行延拓優化分解頻譜圖Fig.6 EEMD and parallel extension optimization decomposition spectrum

2.2 SVR預測模型構建

通過改進的EEMD算法得到6個平穩分量，使用SVR預測模型，代入遺傳算法尋得的參數，對各分量進行分別預測并將預測值進行集成得到預測價格。

遺傳算法運行中，設置參數迭代次數最大為100次，懲罰因子、核參數的邊界設置均為[0,100]，遺傳算法默認適應度函數值越大即代表尋找參數為最優，本研究選用均方誤差MSE的倒數作為適應度函數，作為迭代尋優的標準，具體形式為：

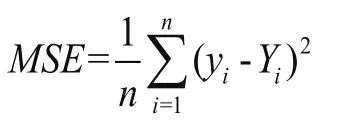
式中，yi(i=1,2,3,....n)為模型預測值，Yi(i=1,2,3,....n)為實際數值，n為數據點的個數，最終得到模型的最優參數。

2.3 預測結果與分析

為了衡量所提出方法的有效性，分別采用MSE、均方根誤差（Root Mean Square Error，RMSE）以及平均百分比誤差（Mean Absolute Percentage Error，MAPE）3種常用的誤差指標評價模型的預測精度，具體描述形式如下：

（1）均方誤差：見2.2公式

（2）均方根誤差

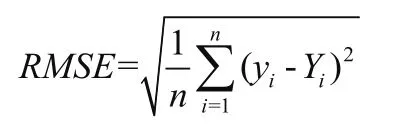
（3）平均百分比誤差

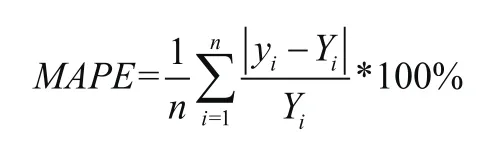
式中，yi(i=1,2,3,....n)為模型預測值，Yi(i=1,2,3,....n)為實際數值，n為樣本數量。

為了評價所提出模型的預測效果，選用無端點延拓EMD、端點作為極值點EMD、平行延拓后EMD、平行延拓后EEMD 4種分解方法和原始價格數據直接預測5種模型，將預測結果進行分析比較，在3種預測評價指標下的具體結果見表1。從表1可以看出，平行延拓后EEMD分解模型的預測精度相對其他方法有較大提高，普遍高于原價格直接預測、無端點延拓EMD和把端點作為極值點EMD 3種預測模型，相比于平行延拓EMD模型也有較好的預測效果，體現出更好的預測性能。

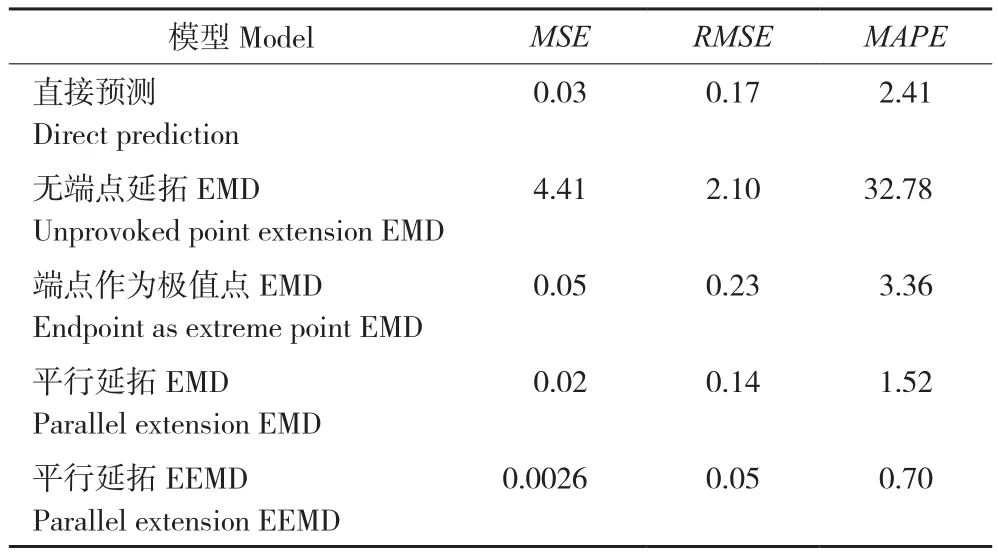
表1 模型預測性能比較Table 1 Comparison of different model prediction performance

5種預測模型的效果如圖7和圖8所示。通過預測圖我們可直觀發現平行延拓后EEMD模型的預測效果和真實值相近，而其余幾種處理方法都有較大誤差。

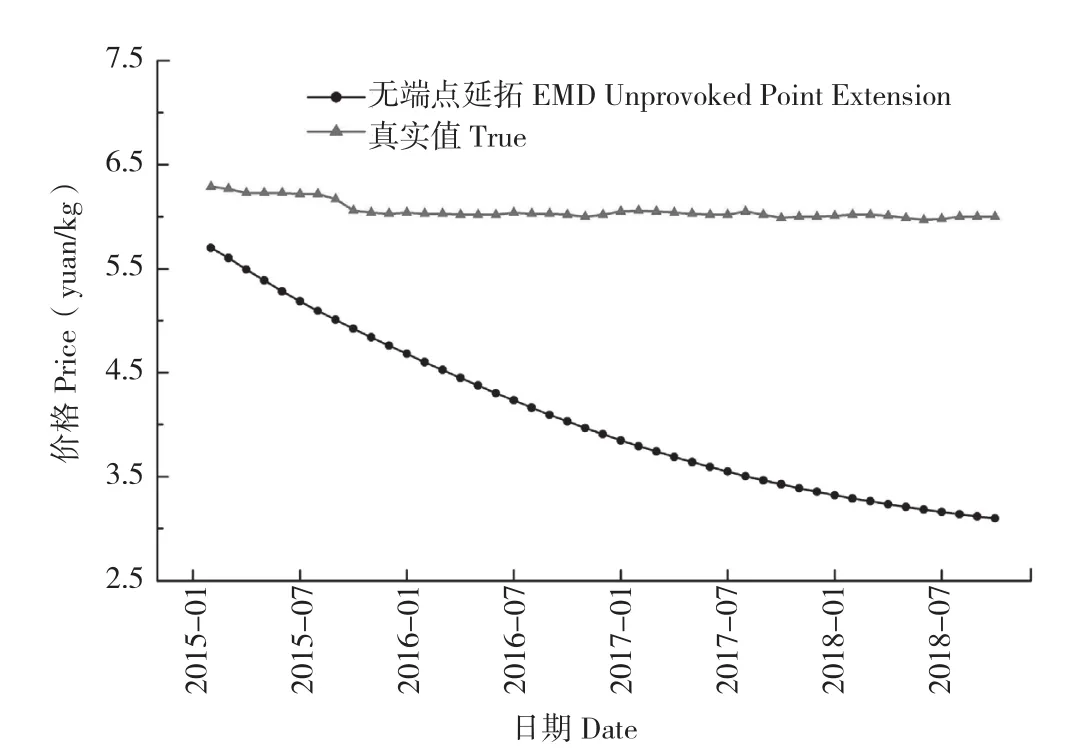
圖7 無端點延拓EMD預測結果Fig.7 EMD prediction of unprovoked point extension

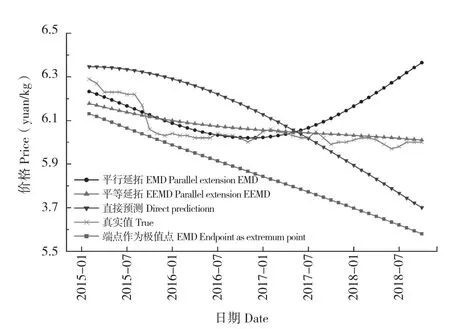
圖8 其余4種模型預測結果Fig.8 Prediction result of the remaining four models

3 討論

本研究考慮大豆時間序列在實際分解過程中存在模態混淆和端點效應問題，對EMD分解方法進行了改進，在分量預測模型SVR的建立過程中，通過遺傳算法實現模型參數的優化選擇，將不同分量的預測結果集成，以實現準確預測，對于指導大豆的生產和進出口貿易具有較高的指導意義：（1）經過平行延拓后的EMD算法相對于直接EMD預測的效果更好，通過對序列兩端進行延拓，構造出新的極值點再進行分解，有效抑制了EMD分解中存在的端點效應問題[12]。（2）EEMD有針對性地引入白噪聲，有效解決了模態混疊問題，通過EEMD得到不同的分解序列，與傳統預測方法相比，可以得到平穩的時間序列，對每個分量用以相應的具體模型，不同的參數選擇可以得到更為精準的預測效果[13-15]。（3）相對于平行延拓EMD分解，通過平行延拓出極值點再進行EEMD分解，得到的分解序列預測效果更好、精度更高，可以同時抑制模態混疊和端點效應造成的影響[16]。（4）遺傳算傳通過把問題解的組成空間映射為遺傳空間，把可能的解編碼成一個向量即染色體，通過不斷計算各染色體的適應值，選擇最好的染色體，從而獲得最優解，通過引入遺傳算法優化SVR模型的懲罰因子和核參數，能夠較好解決預測模型中的參數優選問題，有效優化預測模型[17-19]。

4 結論

本研究將EMD信號分解處理的方法運用到大豆價格預測中，將原本非平穩、非線性的數據分解為若干平穩數據分量和殘余項，通過添加白噪聲和對原始時間序列進行平行延拓的處理方法，有效地解決了模態混疊和端點效應問題，對每一個 IMF 分量分別用不同的支持向量機模型，并對其通過遺傳算法單獨選擇最優的核函數和參數，再進行集成預測，相對于傳統的預測算法，提高了大豆預測精度。