基于K-means聚類方法的物流多配送中心選址優化研究

王 勇，黃思奇，劉 永，許茂增

(1.重慶交通大學 經濟與管理學院，重慶 400074；2.電子科技大學 經濟與管理學院，四川 成都 611731)

0 引言

物流配送中心選址問題是城市物流配送網絡優化的初始環節，是指在一定數目的備選址位置中選擇一定數量的地址作為配送中心的規劃過程。基于聚類方法的多配送中心選址問題研究，是將涉及選址多重影響因素的聚類方法與選址決策方法相結合，選擇合理的配送中心數量和位置作為優化目標，進而保證物流系統規劃的可持續發展。

國內外學者在配送中心選址問題研究方面已取得了較多研究成果。部分學者通過目標函數和約束條件構建定量化的數學模型進行選址問題研究，并通過啟發式算法進行求解，Dan和Yu[1]提出了應用隨機規劃模型研究不確定需求下配送中心的選址問題。李東等[2]設計了貪婪取走的啟發式方法用于研究設施失效情況下的軍事物流配送中心選址問題。姜燕寧和郝書池[3]構建了以系統總成本最低為目標的庫存配置與選址決策模型，研究了隨機需求情形下多級配送網絡的庫存-選址優化問題。李明等[4]根據產銷平衡的思路建立相應的數學模型研究了多物流配送中心的選址問題。Ye[5]研究了基于梯形直覺模糊信息的多準則群決策，提出了將語言屬性通過模糊數轉化，從而進行定量計算。而對于一些難以應用數據進行衡量的問題，定性研究體現了優越性。Awasthi等[6]提出在選址因素不確定條件下運用模糊集理論進行選址問題研究。王勇等[7]人提出先建立多配送中心評價指標體系的方法，再結合三角模糊數和語言變量值來研究多配送中心的選址問題。樓振凱和戴曉震[8]應用模糊層次分析法和改進的理想解排序法(TOPSIS)研究了模糊條件下的物流配送中心選址評價問題。賈瑞玉和宋建林[9]應用K-means方法研究了基于聚類中心優化的最佳聚類數確定方法。梁昌勇等[10]設計了基于TOPSIS方法的多屬性群排序方法，并將其應用于配送中心的選址排序問題研究中。然而，考慮城市物流多配送中心選址過程的多重因素影響，并進行方法融合方面的研究設計較少。

針對城市多配送中心選址過程需要考慮較多因素且因素間具有復雜相關性的問題，首先，應用模糊理論集理論，將語言變量模糊數和梯形模糊數相結合，在建立的綜合評價指標體系下對各指標權重及其各指標進行評價；其次，應用K-means聚類方法對備選配送中心進行分類；最后，應用TOPSIS方法進行各聚類中心備選址的排序計算，得出多配送中心的優化選址方案，并進行了實例驗證。所提的多配送中心選址優化方法，為城市物流網絡優化中的選址優化相關問題提供了新的研究思路。

1 配送中心選址的評價指標體系和相關語言變量

1.1 配送中心選址的評價指標體系

配送中心選址過程涉及到的自然環境因素(氣候條件、地質條件、水文條件和地形條件)和經濟因素(建設費用、運輸費用和運營成本)屬于確定選址的前提條件和外部因素，而選址過程涉及的交通運輸因素(道路設施、可達性和公共設施狀況)和信息質量(信息基礎設施和信息準確性)等是確定選址的決策因素，同時配送中心業務活動質量和客戶服務質量屬于配送中心選址確定并建立后運營中的管理范疇，因此，將配送中心評價體系分成兩級指標，并分別從自然環境因素、經濟因素、交通運輸因素、信息質量、配送中心業務活動質量、客戶服務質量這6個方面對配送中心進行綜合評價，具體如圖1所示。

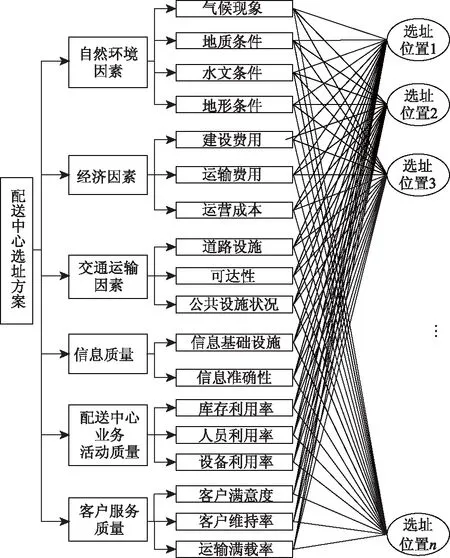
圖1 多配送中心選址的評價指標體系Fig.1 Evaluation index system for location selection of multiple distribution center

運用梯形直覺模糊數[11-12]表示各配送中心二級準則指標下的各屬性權重值和各專家對配送中心評價指標下各屬性的評價值。運用模糊集成的方法，將其評價值集成到一級指標上，最終得到綜合評價值。

1.2 語言變量和對應的模糊數設計

根據建立的配送中心綜合評價指標體系，將相關語言變量和相應的梯形模糊數，得到表1的對應關系，運用其描述配送中心評價指標體系下各屬性權重的重要度及其權重。

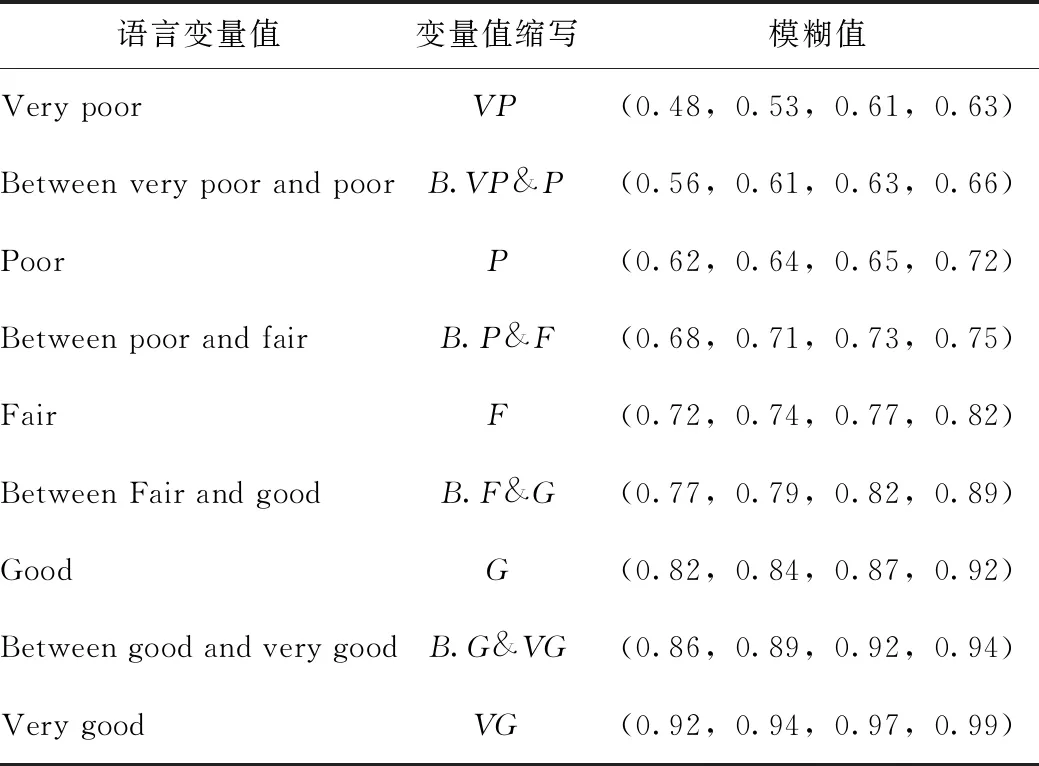
表1 語言變量值及對應的模糊數表

運用上述語言變量值，結合相應的梯形直覺模糊數值，對綜合評價指標體系中不同屬性的重要度進行評價，從而確定屬性權重。對各準則指標權重進行評價時，將語言變量值中的poor替換為low，fair替換為moderate，good替換為high，而其梯形直覺模糊數值不變，即將表1中的語言變量值縮寫轉變成 VL-VH。

2 基于配送中心評價指標體系的聚類研究

2.1 相關定義

針對表 1 中的語言變量及相應模糊數表，邀請多位專家對備選配送中心在綜合評價指標體系下的二級準則指標進行評價，并對二級準則指標的自身權重進行綜合評價，相關定義和符號如下：

定義1 參與指標評價的專家人數為s，p表示參與評價的專家集合：p={pi|i=1,2,…,s}。

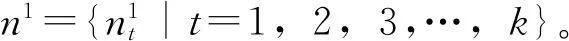
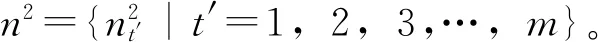
定義4設定備選配送中心的個數為n，D表示備選方案的集合是D={DZ|z=1,2,…,n}，通過聚類算法可將備選方案分為F類，C表示備選方案的聚類集合：C={Cg|g=1,2,…,F}。

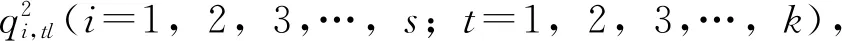
定義6 備選配送中心的聚類數據集表示為：w=(x1,x2,…,xn)，其中選出的k個聚類中心表示為：(β1,β2,…,βk)，每個聚類對象到聚類中心的距離使用歐式距離表示為：

d(xi,xj)=

(1)

定義7Y為一個給定的數據集，假定在數據集Y中有n個聚類子集，分別表示為：y1,y2,…,yn，其中，每個聚類子集中的樣本數量表示為：k1,k2,…,kn；每個聚類子集均有一個聚類中心點，其聚類中心表示為：g1,g2,…,gn。因此，設定誤差平方和準則函數公式E為：

(2)

2.2 模糊聚類方法

備選配送中心的聚類方法包括以下兩個步驟：(1)運用模糊集成方法，對備選配送中心評價指標評價體系中的二級指標進行模糊評價，再結合二級指標體系中各自的權重，將二級指標的評價值集成到一級指標上。(2)將集成到一級指標上的指標值，通過K-means算法同模糊聚類算法結合，對備選配送中心進行聚類。

2.2.1二級準則指標下的模糊集成方法

(3)

式中，s為參與評價的專家人數;tk為一級指標屬性t下包含的二級準則指標的個數;⊕為矢量相加，?為矢量之積。

2.2.2模糊K-means聚類方法

模糊K-means聚類方法的具體實現步驟如下：

(1)若梯形模糊數的表示形式為：w=(a,b,c,d)，則可將p(w)表示為梯形模糊數的集成數值：

(4)

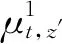
(5)

(3)首先從備選的配送中心中選擇k個對象作為初始的聚類中心，確定簇的數量為k。

(4)將ej,1，ej,2，ej,3作為聚類的輸入，運用歐式距離公式計算出聚類對象到k個聚類中心的歐式距離d(xi,xj)，根據歐式距離并結合各聚類中心位置劃分不同的聚類單元。

(5)在已劃分好的聚類單元中，重新計算各個聚類單元的樣本平均值，并將其值作為聚類單元的新中心。

(6)重復上述步驟(4)和(5)，并進行聚類結果的比較分析，進而計算公式(2)中的E值，E值越小，表示聚類結果越理想，當聚類中心不再改變或達到指定的迭代次數時，則聚類結束并得到聚類結果。

2.3 模糊聚類方法的有效性指標

應用模糊K-means聚類方法[13]進行計算時，由于k值是事先擬定的，為了評判最終聚類結果的合理性，需要對聚類結果的有效性進行評價驗證。聚類結果有效性[13]的評價指標可以包括兩個方面，一方面是外部標準，若得出的聚類結果與參考準則保持一致，則為合理的聚類結果，否則，為不合理的聚類結果；另一方面是內部指標，即通過聚類有效性指標確定最佳的聚類數。通常應用內部指標評價聚類結果具有一定的科學性和合理性。設定DB樣本的類內離散度和各聚類中心間距：

(6)

(7)

d(hi,hj)=‖υi-υj‖

(8)

式中，n為聚類數目；s(ni)和s(nj)分別為每類中的所有樣本到其聚類中心的平均距離；d(hi,hj)為類與類之間的中心距離；ni為類i中的樣本個數；υi，υj分別為聚類中心。由此可知，DB越小表示類與類之間的相似度越低，從而聚類結果越佳。

3 TOPSIS排序方法

結合模糊聚類方法得到的聚類結果，應用TOPSIS排序方法進行聚類單元內的備選址評價排序[11]。若有h個評價對象和o個評價指標，則原始評價矩陣可表示為：

(9)

對指標進行標準化和去量鋼化處理，具體計算公式如下：

(10)

(11)

(12)

(13)

TOPSIS排序方法[14]是檢驗各評價對象和正理想值、負理想值距離進行排序。其中，正理想值由待評價對象中每個屬性值的最優值組成，而負理想值由待評價對象中每個屬性值的最劣值組成，進而計算出每個方案與最優和最差值的距離。最優值和最差值分別表示為Z+和Z-，則n個評價方案的歐式距離公式如下：

(14)

(15)

4 算例分析

4.1 實例相關數據

以某企業在重慶市選擇配送中心為案列，經過考察后有20個備選配送中心，分別用D1，D2，…，D20來表示。同時邀請5位專家對建立的指標體系中二級準則指標下的備選配送中心的選址評價及二級準則指標權重進行評價，其中5位專家用P={P1,P2,P3,P4,P5}表示。專家運用表1中語言變量值的模糊數，對指標評價體系下的二級準則指標的權重進行評價(如下表2所示)。運用2.2節中提到的二級準則指標下的模糊集成方法，應用模糊集成方法將相應的二級準則指標的權重值和專家對其的評價值集成到一級指標上，然后，運用2.2.2節中提到的方法將集成到一級準則指標上的值重新拆分成3個屬性值，并表示為：qej,1,qej,2,qej,3。

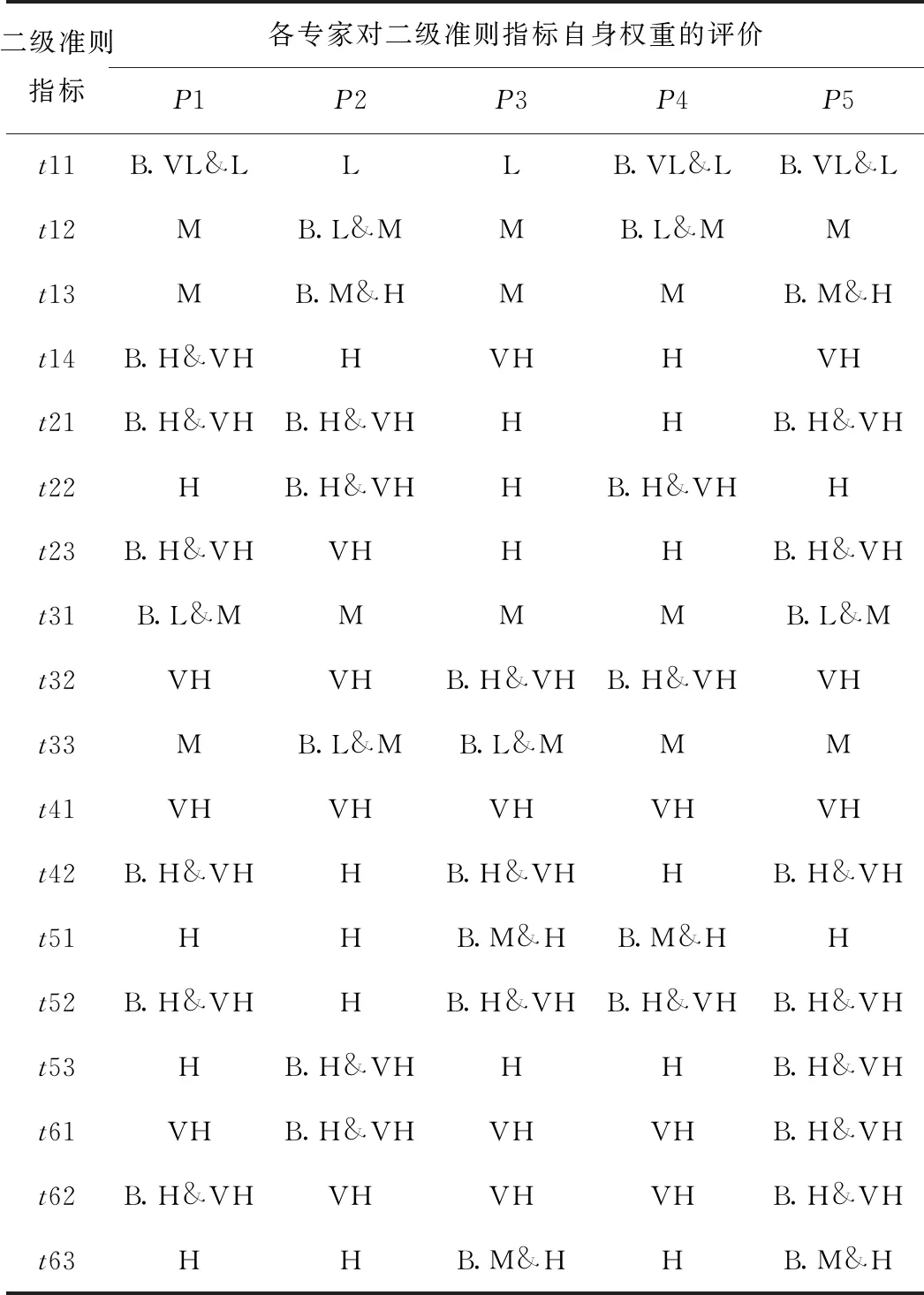
表2 各專家對二級準則指標權重的評價

通過表2中二級準則指標權重的評價值和表1中的模糊數表相結合，得到二級準則指標下的評價值，通過模糊集成方法，將二級準則指標下的評價值集成到一級準則指標上。得到各備配送中心的綜合評價值，由表3所示：

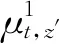
4.2 聚類和選址方案

結合選址方案的時效性和合理性，本研究將聚類數目設定在3到5之間。根據上述聚類有效性指標的計算公式(6)，(7)，(8)，具體的聚類結果和不同聚類結果的聚類有效性指標如表5和圖2所示。

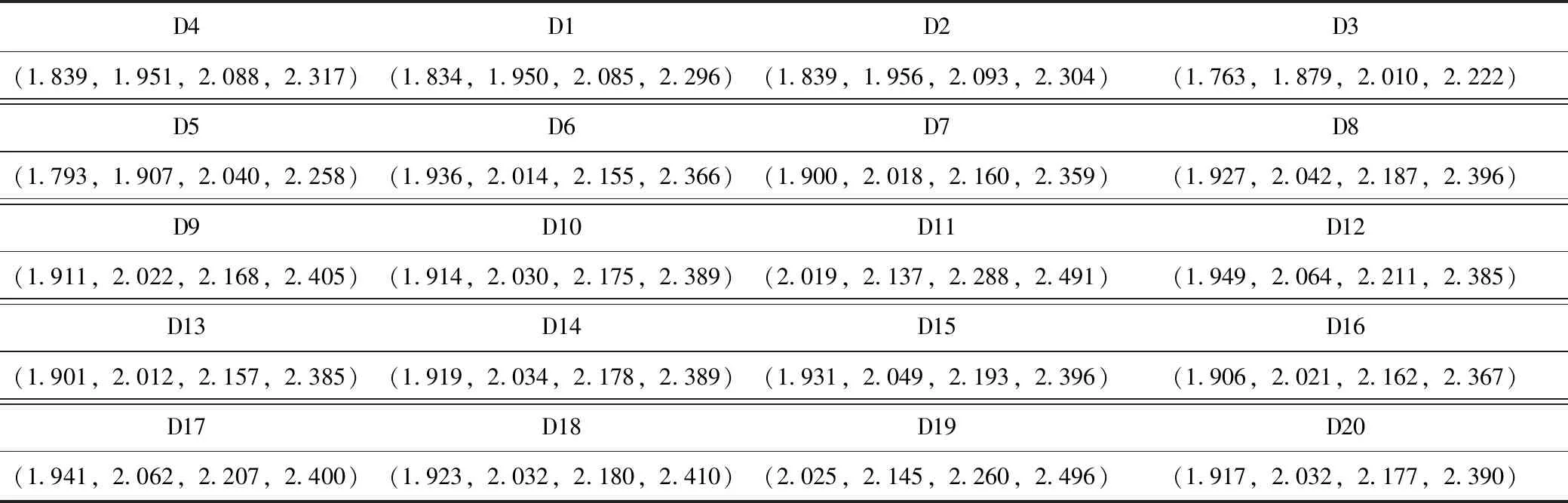
表3 備選多配送中心選址方案的綜合評價

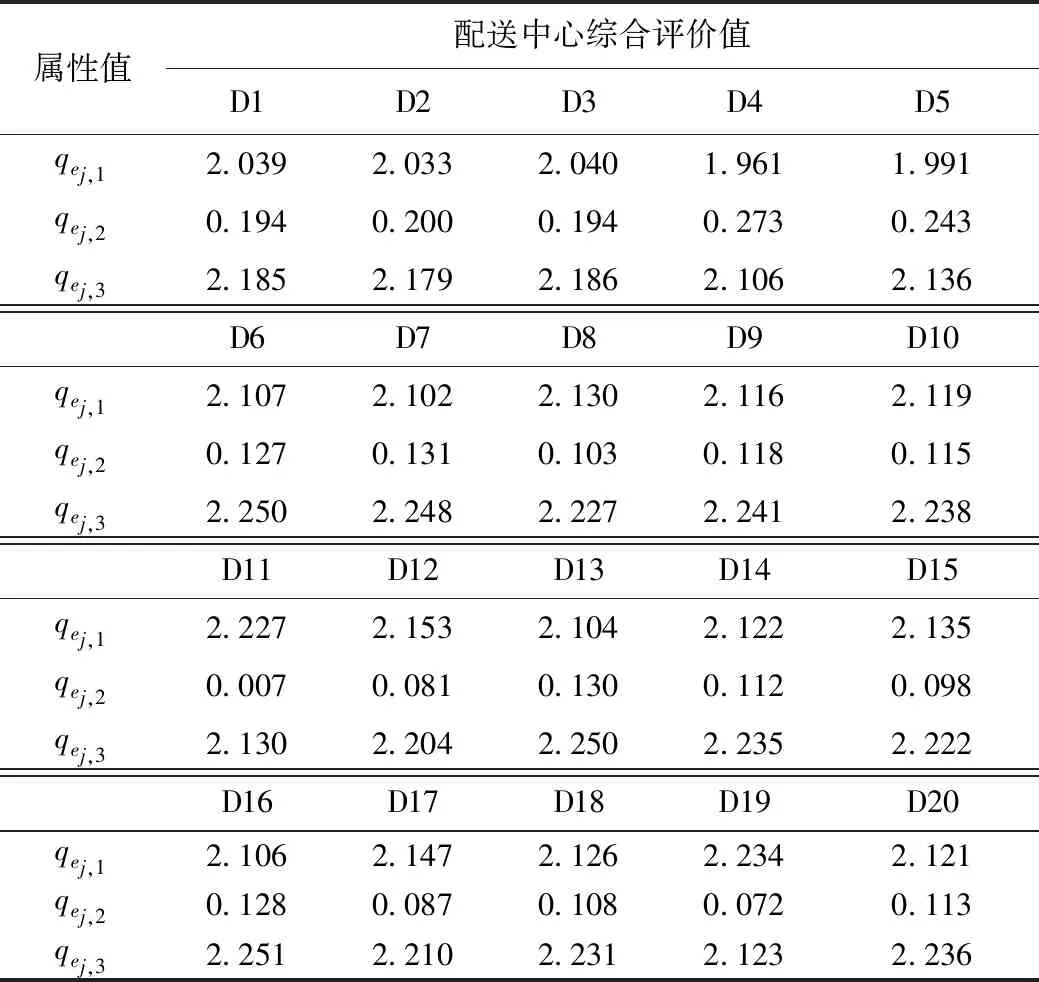
表4 備選配送中心的隸屬度函數值

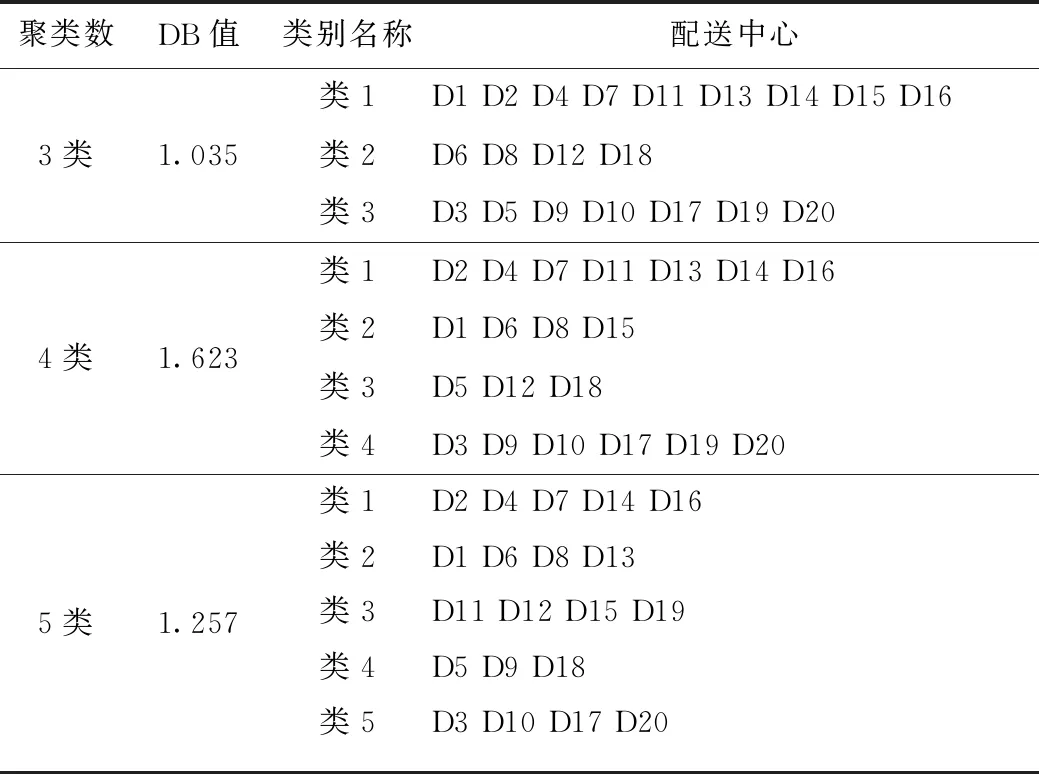
表5 聚類數為3-5的聚類結果

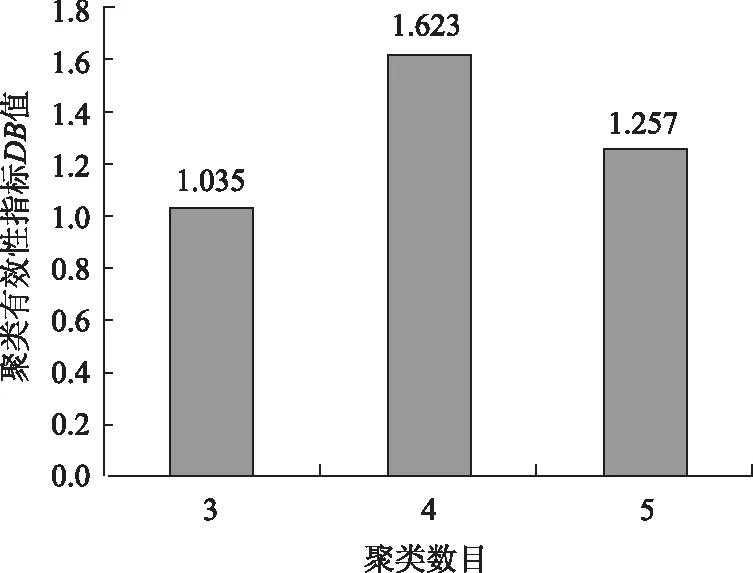
圖2 不同聚類數目的聚類有效性指標Fig.2 Clustering Validity Indicators of different cluster numbers

當DB越小時，其聚類效果越好，表明聚類單元中同類別個體間的差距越小，而不同類別個體間差距越大。因此當聚類數為3時得到最佳聚類數目： {D1, D2,D4,D7,D11,D13,D14,D15,D16}，{D6,D8,D12,D18}，{D3,D5,D9,D10,D17,D19,D20}。為了進一步驗證聚類結果的有效性，分別應用文獻[17]提出的一種基于Spark框架的改進DBSCAN聚類算法和文獻[18]提出的BIRCH聚類算法進行聚類比較分析，如表6所示。

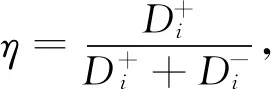
表6 3種聚類方法的聚類結果和有效性指標

應用模糊K-means聚類方法后，在每個聚類單元中運用TOPSIS排序方法選取一個配送中心為最終配送中心。根據上表中的計算數值，可知當η值越小，其評價結果越高。因此，選取最小的η值作為各類中的最優評價值，即選出最優配送中心為D6，D9，D16。結合圖2可知，此方法選出的配送中心位置合理。因此，基于模糊K-means聚類算法的物流多配送中心選址方法，將集成后的隸屬度函數重新拆分成多個隸屬度函數子屬性值，能夠挖掘有效的聚類屬性特征和劃分更合理的聚類方案，可以保證最終得到較優的配送中心選址方案。綜合比較上述方法，本研究所提方法更具實踐應用性。

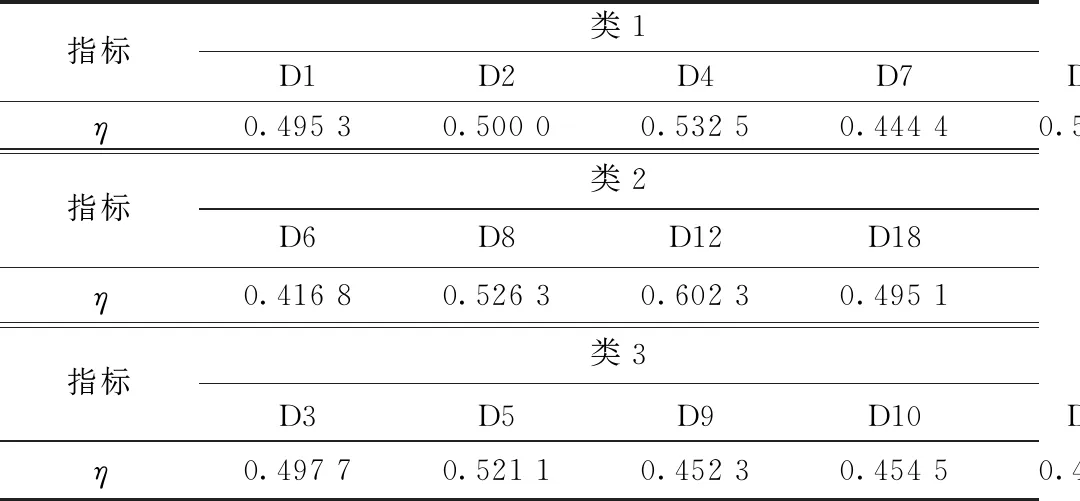
表7 聚類數為3的選址排序

5 結論

研究了物流網絡中的多配送中心選址問題，首先，對一系列備選配送中心建立了評價指標體系，通過對備選配送中心在指標體系中的二級準則指標及其權重進行綜合評價，并將語言變量模糊數和梯形模糊數相結合，得到二級準則指標及其權重的評價值；其次，應用模糊集成方法將二級準則指標的評價值集成到一級準則指標上，并通過隸屬度函數進行屬性拆分；最后，將拆分屬性值作為模糊K-means聚類方法的輸入，并通過聚類有效性指標值選取合理的備選配送中心聚類方案，進而應用TOPSIS方法計算出聚類后各聚類中的排序，從而選出最優配送中心選址方案。最后，應用實例驗證了所提方法的有效性，該方法也能應用到多級物流網絡的配送中心選址過程中。