基于模態識別的短索索力識別方法

劉晨凱， 鄭萬山

(1. 中建三局工程設計有限公司，湖北 武漢 430074；2.橋梁工程結構動力學國家重點實驗室，重慶 400067)

0 引言

拉索索力的變化通常是結構退化的關鍵指標，同時也影響結構的內力分布[1]，準確快速地評估索力是非常重要的。頻率法由于其方便的激勵方式和可靠的測量精度，成為最廣泛應用的技術。對于長索，頻率法測試精度滿足工程應用。但是對于短索，經典索力計算公式是在理想的兩端鉸接條件下得到的,對于一般邊界條件將面臨計算長度選取的難題[2]；同時，拉索抗彎剛度的選取對索力測試精度的影響同樣不容忽視。

針對一般邊界條件下的短索索力識別，前人進行了大量的研究。2007年Nerio Tullini等人在已知拉索抗彎剛度前提下，除拉索兩端振幅為零的邊界條件外，引入3個已知測點的振幅，建立方程組，求解得到拉索索力及兩端的轉角剛度[3]。2011年Suzhen Li等人在已知拉索抗彎剛度前提下，選取至少5個測點的振動數據，利用撓度函數和應變函數之間的關系式得到方程組，最終求得索力與兩端的支撐剛度和轉角剛度[1]。2015年李柯君等人在已知拉索抗彎剛度前提下，利用拉索的某個自振頻率和相應振型的幾個振動分量，在未知邊界條件的情況下識別索力，最終確定拉索的邊界等效彈簧的剛度值[4]。2015年晏班夫等人提出的方法將零幅度點間的距離作拉索計算長度代入到索力計算式中，從而求得索力[5]。

除了各階模態頻率及質量參數外，現有測試理論仍需要在獲取拉索截面抗彎剛度信息的基礎上才能實現索力識別[1-6]。實際拉索通常是由鋼絞線或者平行鋼絲構成的，其內部鋼絲間的黏結力大小存在離散性，因此即使是同一型號的拉索，不同拉索的截面抗彎剛度也具有離散性的特征。在已知拉索型號的前提下，拉索的實際抗彎剛度仍難以確定。因此有必要開展在未知抗彎剛度的前提下，一般邊界條件的短索索力識別研究。

1 理論公式推導

1.1 理論公式推導

受恒定拉力歐拉伯努利梁振動方程的通解表達式[7]為：

φ(x)=A1sin(q1x)+A2cos(q1x)+

A3sh(q2x)+A4ch(q2x)，

(1)

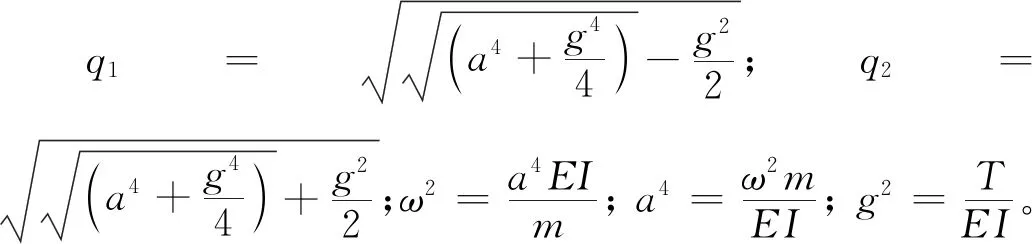
又知：

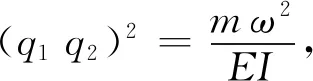
(2)

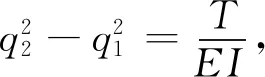
(3)

(4)

(5)

式中,EI為索的抗彎剛度;m為線質量;T為索的拉力;ω為拉索自振圓頻率。

下面對索力計算公式進行整理，以得到一個適用于一般邊界條件的索力計算公式。

將式(5)代入式(3)中得：

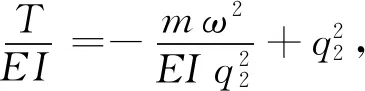
(6)

化簡得：

(7)

又因

ω=2πf，

(8)

可得：

(9)

同理將式(4)代入式(2)中得：

(10)

(11)

(12)

當邊界條件為兩端鉸接時，索力計算公式[7]為：

(13)

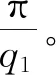
1.2 識別方法研究

對適用于梁模型而邊界條件復雜的短索，可以使用式(12)計算索力。計算索力所需獲取的參數有拉索每延米質量參數m、自振頻率f、參數q1及抗彎剛度EI，質量參數m及各階自振頻率均易獲得，則索力識別的關鍵轉變為參數q1及抗彎剛度EI的識別問題。

在具體參數識別時，振型函數中非線性項括號內有兩個未知數，假設仍然能夠通過建立方程組求解。通過某階模態下5個已知點的振型可以建立方程組：

φ(xi)=A1sin(q1xi)+A2cos(q1xi)+

A3sh(q2xi)+A4ch(q2xi)，

(14)

式中i=1,2,3,4,5。

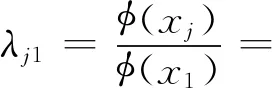
式中j=2,3,4,5。

可得：

A1sin(q1xj)+A2cos(q1xj)+A3sh(q2xj)+A4ch(q2xj)=

λj1[A1sin(q1x1)+A2cos(q1x1)+A3sh(q2x1)+A4ch(q2x1)]， 即A1[sin(q1xj)-λj1sin(q1x1)]+A2[cos(q1xj)-λj1cos(q1x1)]+A3[sh(q2xj)-λj1sh(q2x1)]+A4[ch(q2xj)-λj1ch(q2x1)]=0，

式中j=2,3,4,5。

由以上方程組可知，即使增加方程的數量，對括號內的未知數求解并沒有幫助。括號內的未知參數q1,q2通常的求解方法是，將方程組轉化成矩陣形式，然后利用系數行列式等于0來求解。q1，q2滿足式(2)、式(3)，加上行列式等于0，已知方程數量為3個，未知參數為q1，q2，T，EI4個，有無窮解。

因此在未知拉索抗彎剛度EI的情況下，只能采用曲線擬合的方法通過多個點的振型數據來擬合振型函數通解，得到參數值q1，q2，從而求得索力值及拉索抗彎剛度。

2 短索索力測試方法研究

根據前文的分析可知，在未知拉索抗彎剛度的情況下，只能通過曲線擬合來獲取未知參數q1，q2的值。擬合得到參數q1，q2的值后，有兩種方式來求得索力值及抗彎剛度：

(1)同時識別參數q1，q2，然后通過二者的關系式求得拉索索力及抗彎剛度EI；

(2)識別參數q1，q2其中的一項，選用索力計算公式(7)或者(12)計算索力值，抗彎剛度由不同階模態建立的形如式(7)或式(12)的方程組聯立求解得到。

2.1 短索模態振型特征

本研究通過分析各類邊界條件下梁模型的各階模態振型特征，得到如下結論：

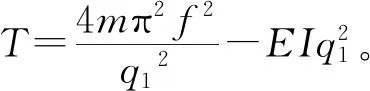
2.2 短索索力測試方法介紹

根據前文分析結果可推出一個基于識別參數q1的短吊桿索力識別的方法。具體測試步驟如下：

(1)測量無支撐段拉索長度，計算傳感器布點位置并布設傳感器。

理論上在拉索的全長段均可以布設傳感器，但是由于邊界條件附近振動較弱，信噪比較差，不建議在邊界附近取點。結合拉索的振型特征提出兩種推薦布點方案，具體最優布點位置及數量方案仍需進一步做研究。同時需要指出的是，各傳感器所測量的振動方向應一致，若振動測量方向為豎直向上則各傳感器均布置為豎直方向。

6測點方案：取6個點布設傳感器，假設無支撐段的拉索長度為1，則各點的相對布設位置如圖1所示。

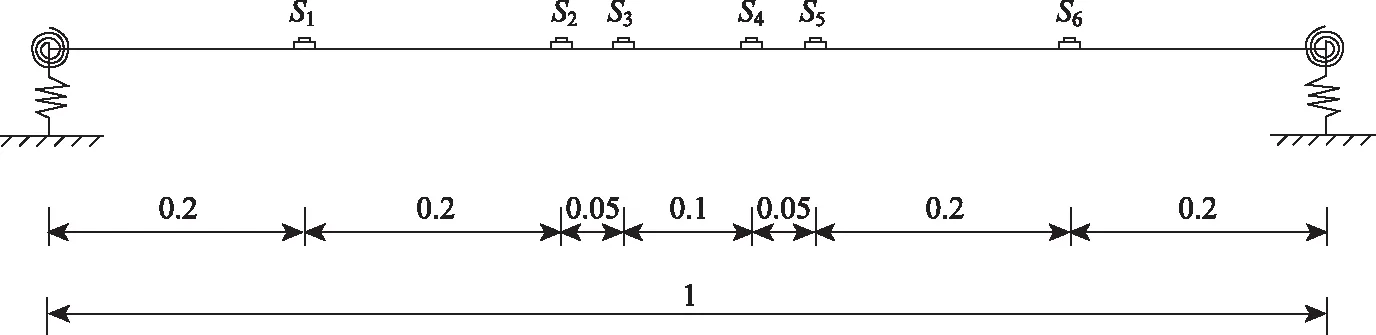
圖1 6傳感器布置方案Fig.1 Arrangement of 6 sensors

8測點方案：取8個點布設傳感器，假設無支撐段的拉索長度為1，則各點的相對布設位置如圖2所示。

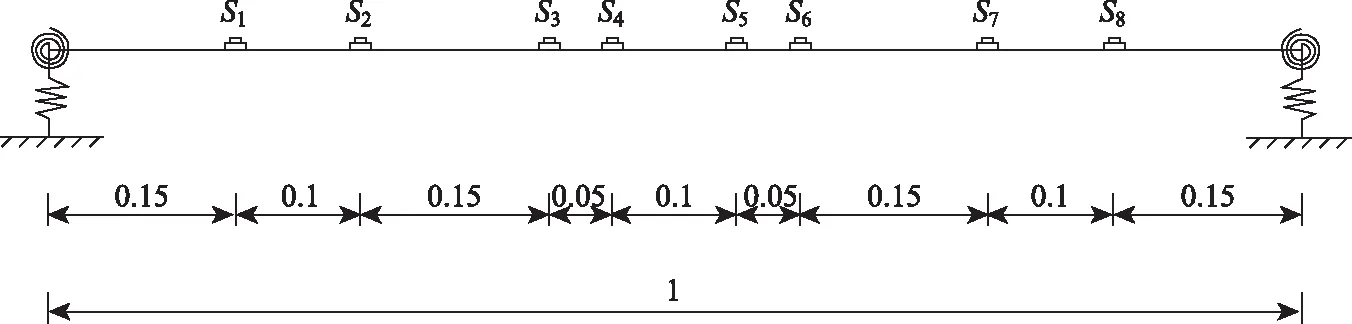
圖2 8傳感器布設位置Fig.2 Arrangement of 8 sensors

這種不等間距的傳感器布設方法既能適用于低階模態的振型函數擬合，同時也能滿足高階模態振型函數擬合的需要。顯然測點數量更多時，得到的振型數據更加豐富，由此擬合得到的振型函數也更加接近真實振型函數。

(2)對拉索進行激勵，采集各傳感器同步時程信息。

(3)對時程數據進行傅里葉變換查看頻率。通過所得頻譜圖判斷各階頻率是否等間距，若為等間距則使用弦模型方法計算，若不等間距則采用梁模型方法計算。

(4)應用隨機子空間法獲得各點振型數據。

隨機子空間法(Stochastic Subspace Identification-SSI)[8-10]是基于環境振動模態參數識別的時域方法，不需要人工激勵，能準確識別系統的頻率，能很好的識別系統的模態振型和阻尼，確定系統的階次是該方法的關鍵。穩定圖法是一種比較新穎的確定系統階次的方法，但該方法容易識別出虛假模態。常軍等人[11]對穩定圖法進行了改進，用模態置信因子來消除虛假模態，將阻尼比的標準放松至40%，提高了隨機子空間方法的識別精度。

本研究應用的即是隨機子空間結合穩定圖的方法來識別各階模態振型，穩定圖示例如圖3所示。

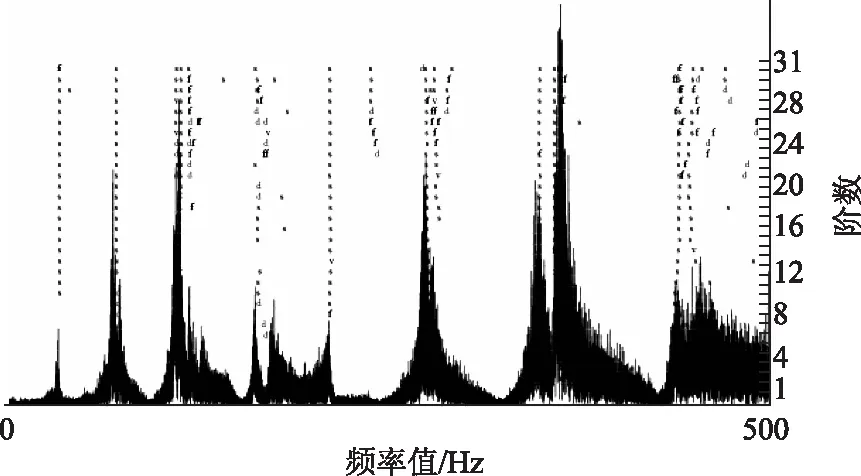
圖3 穩定圖示例Fig.3 Example of a stabilization diagram

(5)預估各階振型半波長范圍并擬合拉索梁模型振型函數。

選用MATLAB中的lsqcurvefit函數[12]對得到的振型數據進行擬合[13]，可得到整個振型函數的表達式，各參數的初始值在預估范圍內程序隨機選擇，最后通過一些評價標準來檢驗擬合的準確度并選出最優擬合。擬合結果評價標準有[14]：殘差平方和(Sum of Squares for Error)、均方根(Root Mean Square)、相關系數(Coefficient Of Correlation)、決定系數(Coefficient Of Determination)、卡方系數(Chi-Square)。

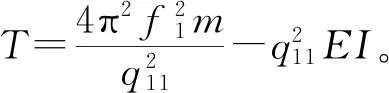
抗彎剛度EI通過第1和n兩階模態聯立方程組求解得來，兩階模態的索力計算公式分別為：

(15)

由以上兩式可得EI表達式為：

(16)

式中，f1，fn分別表示第一階頻率和第n階頻率；q11，q1n分別表示第1階模態的參數q1和第n階模態的參數q1。當計算得到的某個索力值偏離其他大多數索力值較大時，將該索力計算結果去掉，再求剩余索力的平均值。

2.3 測試方法流程圖

本研究測試方法流程圖如圖4所示。

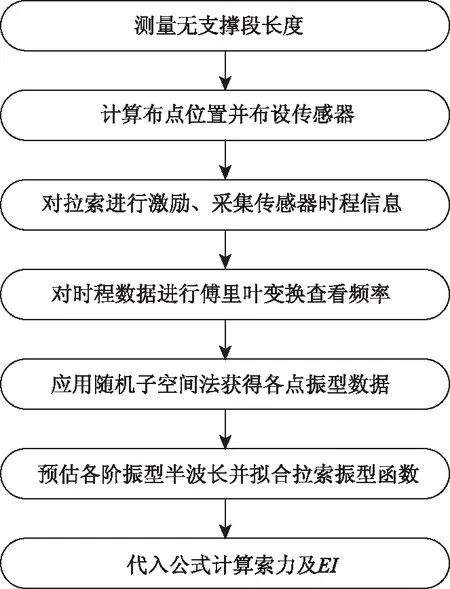
圖4測試方法流程圖Fig.4 Flowchart of test method

2.4 誤差來源及適用范圍分析

2.4.1誤差來源分析

短索索力識別方法的誤差主要來源于以下幾個方面：

(1)歐拉伯努利梁模型帶來的誤差；

(2)各傳感器的振動測量方向不一致導致所得振型與實際振型存在偏差；

(3)噪聲的影響；

(4)測點的布置位置及數量。

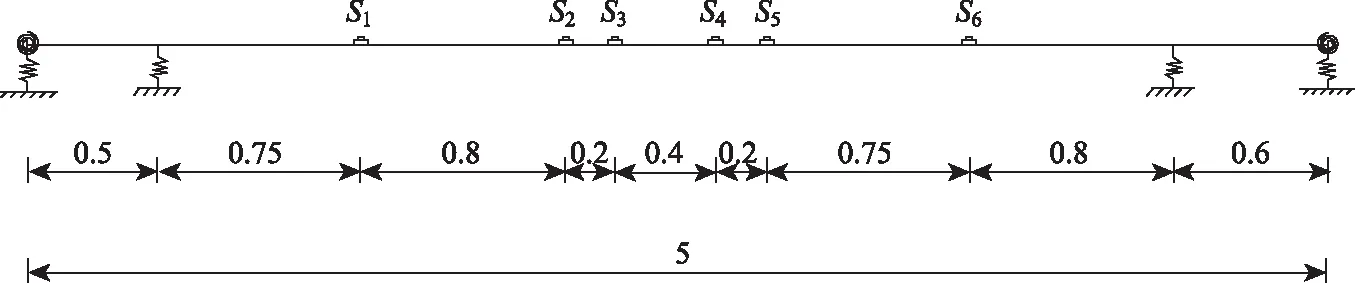
圖6 測點布置(單位：m)Fig.6 Arrangement of measuring points (unit:m)

2.4.2適用范圍

本方法是基于歐拉伯努利梁理論得到的，運用本方法進行索力估算時必須滿足以下條件[15]：

(1)不考慮索剪切變形的影響；

(2)索在橫向作微振動,沿軸線方向位移忽略不計；

(3)索自由振動,不受橫向力作用；

(4)不考慮索的阻尼的影響；

(5)不考慮索的自重影響。

3 數值模擬索力識別研究

為了驗證提出的索力測試方法的實用性，進行有限元模擬短索索力測試[16]。

采用6彈簧邊界條件下beam3梁單元來模擬拉索，如圖5所示，模型兩端點約束軸向位移，用combin14單元模擬彈簧，通過整體降溫來模擬拉索張拉，打開PSTRES。通過改變各彈簧的剛度來模擬邊界條件的改變。假設拉索阻尼為瑞利阻尼[17]，阻尼比取5e-3，α=6.3e-3，β=3.2e-6。

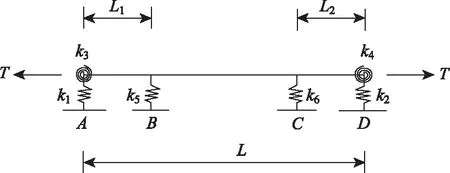
圖5 短索模型示意圖Fig.5 Schematic diagram of short cable model

拉索各項參數為：直徑D=0.15 m，全長L=5 m，L1=0.5 m，L2=0.6 m，索力T=10 000 kN，無量綱參數7.18，每延米質量m=139.96 kg/m。各彈簧剛度參數值見表1。

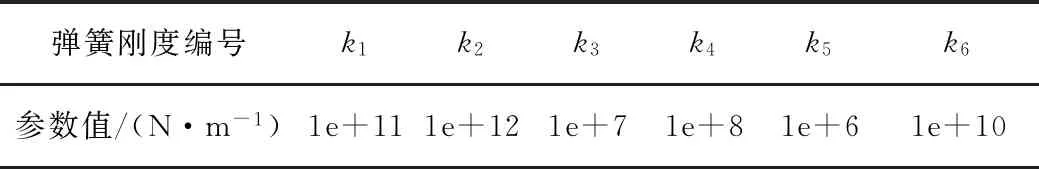
表1 各彈簧剛度值

根據推薦布點方法選取圖6中位置點的響應數據做索力識別計算。

對各點的時域振動數據進行傅里葉變換[18]后可得各階模態頻率如表2所示。

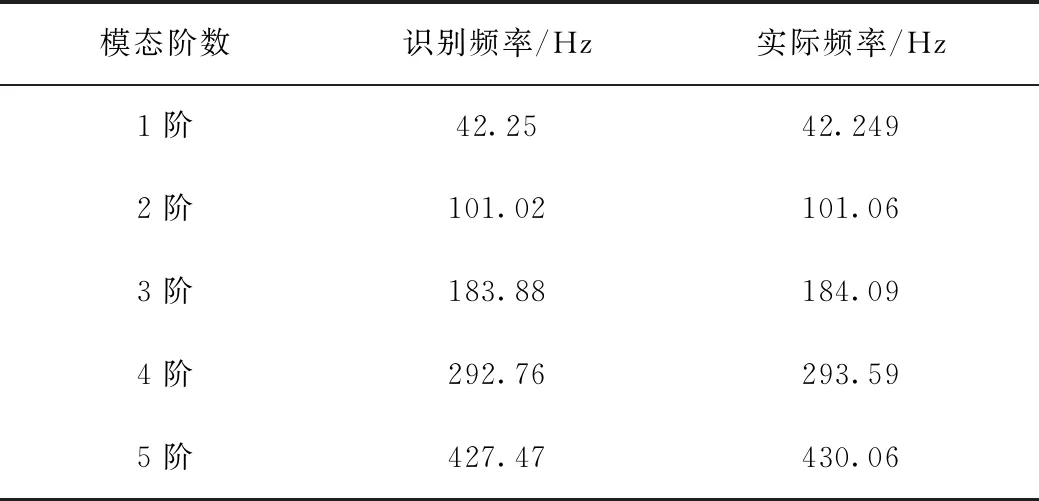
表2 各階模態識別與實際頻率對比

注：此處的1，2，3階編號為各階頻率按從小到大排列所得，但本例為數值模擬，各階頻率均有對應的理論頻率值，所以能夠確定各階模態具體的階數，實際識別時要確定具體的模態階數仍需振型數據來輔助確認。

應用隨機子空間法處理數據后得到的穩定圖如圖7所示，選取小于500 Hz的5階模態，并導出各階模態相應的振型見表3。將各階模態振型數據代入到曲線擬合程序中，擬合結果及評價指標分別如表4、表5所示。

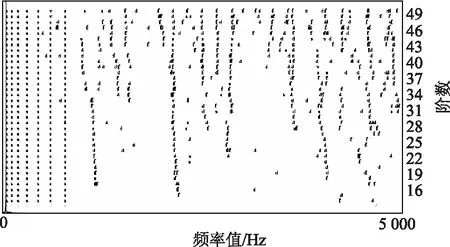
圖7 穩定圖Fig.7 Stabilization diagram

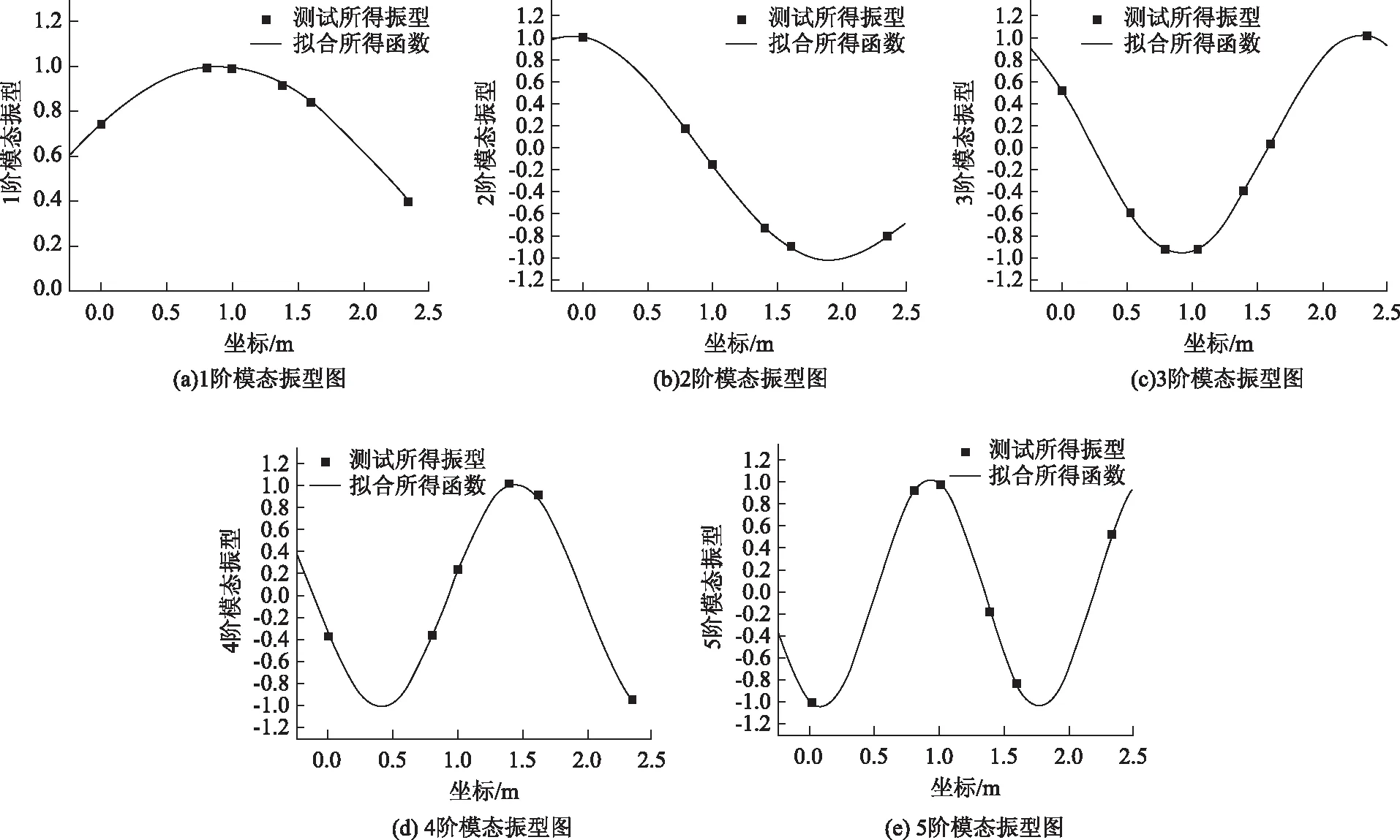
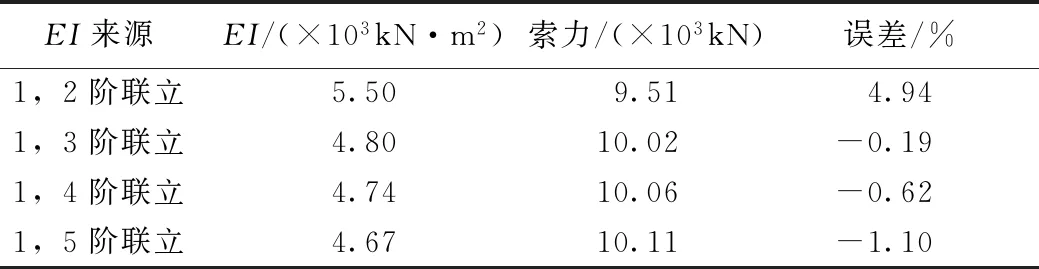
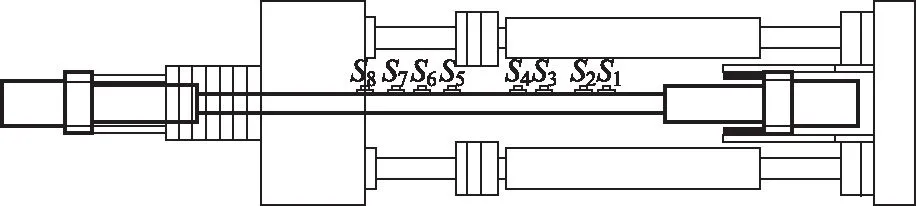
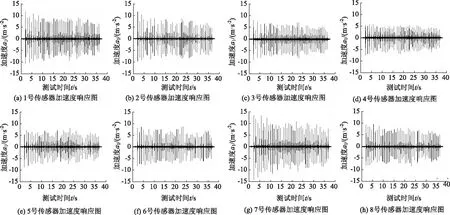
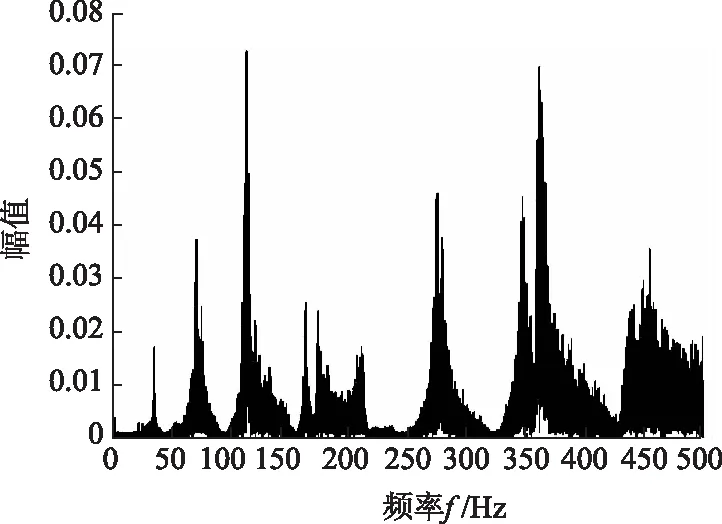
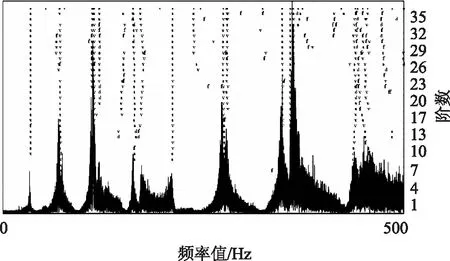
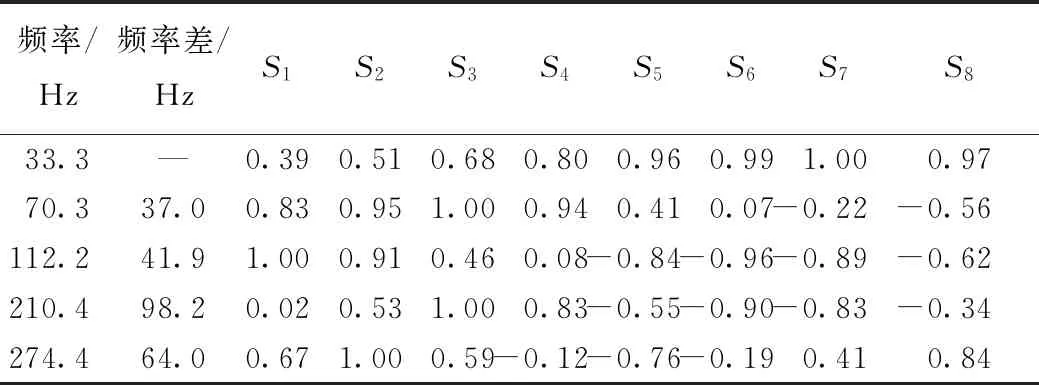
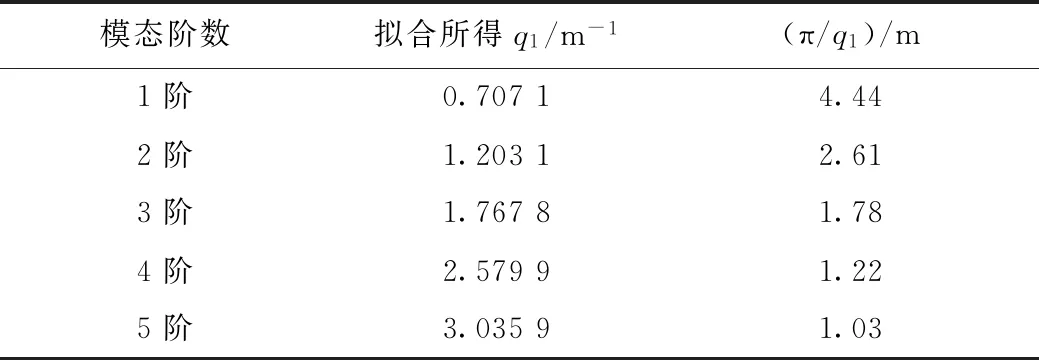
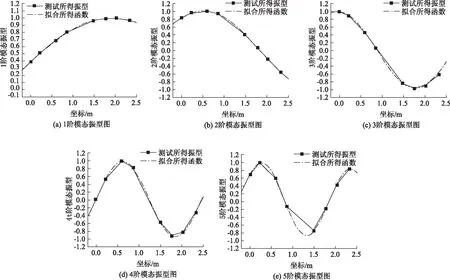
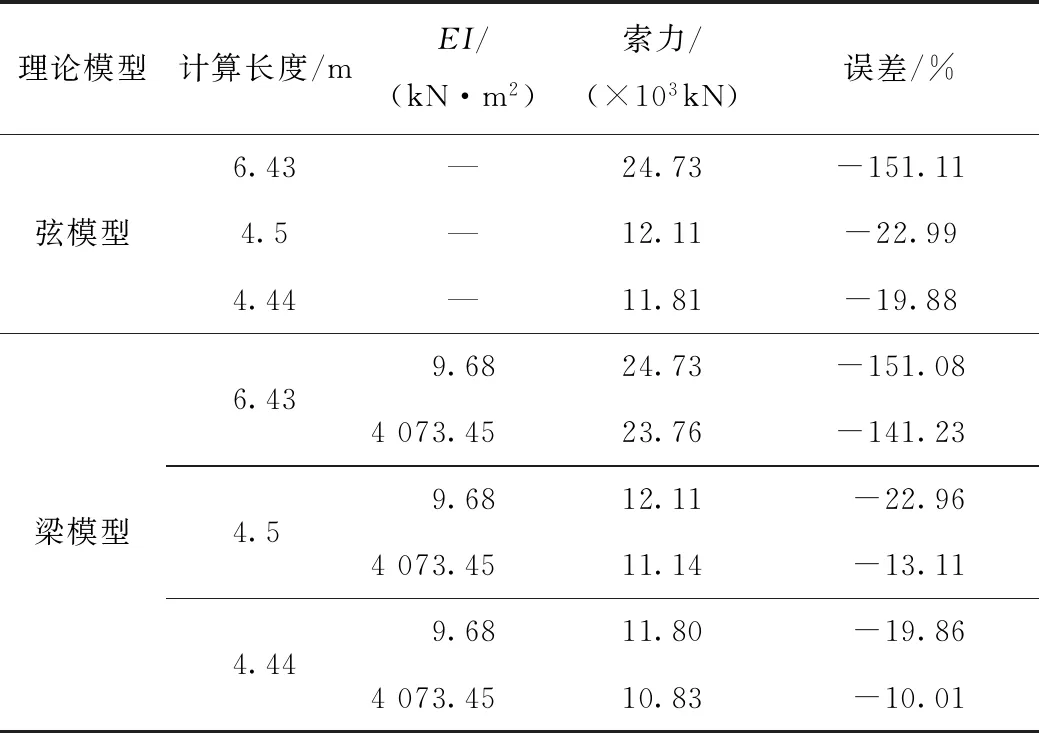
由表5中各評價指標可知，本次擬合結果比較準確。由表4可知，q1的識別精度較高；隨著模態階數的提升，q2的識別誤差增大，甚至程序擬合所得結果不能滿足q1

根據已知的質量參數，各階模態的頻率與q1參數值，采用1階頻率進行索力計算，抗彎剛度EI由1階與其他階模態聯立方程組求解得到，并代入梁模型索力計算式(12)中計算索力值，結果如表6所示。

表3 識別所得各階模態振型

表4 各階模態曲線擬合結果

表5 各階模態擬合結果評價指標

注：圖中橫坐標軸以最左端1號傳感器測點為坐標原點，向右為正方向，單位為m。圖8 各階模態振型圖Fig.8 Curves of each order modal vibration shape

表6 索力識別結果

其中：實際拉索索力為10 000 kN，抗彎剛度為4 845.85 kN·m2。

4 試驗索力識別研究

4.1 試驗簡介

為進一步驗證短索索力測試方法的有效性，進行了實驗室索力測試試驗。

試驗采用人工敲擊拉索，不采集輸入信號，通過輸出信號來識別拉索索力，采樣頻率均為1 000 Hz。試驗系統流程圖如圖9所示，系統由試驗裝置、振動測量部分以及數據處理部分組成。

圖9 試驗系統流程圖
Fig.9 Flowchart of test system

g

圖10 數據采集儀DEWE2-A4照片Fig.10 Photo of data acquisition instrument DEWE2-A4

試驗借助于招商局重慶交科院的拉索疲勞試驗設備，在拉索處于靜止狀態時，應用本方法對拉索索力進行測試。試驗裝置示意圖及現場照片分別如圖11、圖12所示。

圖11 試驗裝置示意圖Fig.11 Schematic diagram of test device

圖12 試驗裝置及拉索現場照片Fig.12 Photo of test device and cable

所用拉索符合規范《斜拉橋熱擠聚乙烯高強鋼絲拉索技術條件》(GB/T 18365—2001)規定，型號為PES(C)7-421，彈性模量為195 GPa，單根鋼絲直徑為7 mm，鋼絲數量為421，鋼絲束公稱截面積為162.02 cm2，拉索總的鋼絲束拉索外徑為181 mm，質量參數m=134.9 kg/m，拉索張拉端安裝有錨索計，在本次試驗時，錨索計顯示索力T=9 848 kN。受現場條件所限，拉索有部分長度范圍內無法布設加速度傳感器，在原有推薦的8測點方案的基礎上調整了傳感器的布設位置，拉索及傳感器位置示意圖及現場照片分別如圖12、圖13所示。

圖13 拉索及傳感器位置示意圖(單位：m)Fig.13 Schematic diagram of cable and sensor positions(unit:m)

圖14 各傳感器加速度響應圖Fig.14 Acceleration response of each sensor

試驗步驟：

(1)測量可布設傳感器段拉索長度，計算傳感器布點位置并布設傳感器。

(2)對拉索進行激勵，采集各傳感器時程信息。

(3)對時程數據進行傅里葉變換查看頻率。通過所得頻譜圖判斷各階頻率是否等間距，若為等間距則使用弦模型方法計算，若不等間距則采用梁模型方法計算。

(4)應用隨機子空間法獲得各點振型數據。

(5)預估各階振型半波長范圍并擬合拉索梁模型振型函數。

(6)代入公式計算拉索索力及EI。

4.2 試驗結果與索力識別

試驗所得各點時程數據如圖14所示。

對各測點加速度時程數據進行傅里葉變換后可得各點頻域加速度響應圖，其特征如圖15所示。

圖15 S1頻域加速度響應Fig.15 Frequency domain acceleration response of S1

使用隨機子空間法處理后可得穩定圖如圖16所示，選取幾階相對穩定的模態提取相應的振型，其結果如表7所示。

圖16 穩定圖Fig.16 Stabilization diagram

表7 識別所得各階模態振型

將各階模態振型數據代入到曲線擬合程序中，擬合結果及評價指標分別如表8、表9所示。

表8 擬合所得各階模態q1值

由表9中各評價指標可知，本次擬合結果比較準確。現將各階模態振型圖與對應的擬合所得曲線放入圖中進行對比，如圖17所示。

表9 各階模態曲線擬合結果評價指標

實際測試的過程中存在某階模態未能識別得到，結合各點的頻域響應圖及振型圖可知3階與4階之間的模態未能識別，但是從表7的頻率差可以看出相鄰兩階模態間的頻率差在逐漸增大，即弦模型在此已經不再適用，應該選用梁模型來計算索力。

此時已知條件有：質量參數m，各階模態的頻率與q1參數值，采用1階頻率進行索力計算，抗彎剛度EI由1階與其他階模態聯立方程組求解得到，并代入梁模型索力計算式(12)中計算索力值，其結果見表10。

表10 索力識別結果

其中：錨索計測得索力為9 848 kN。

由表10可知，抗彎剛度由1階與3，4，5階模態聯立方程組求解得到時，誤差較小；當抗彎剛度由1階與2階模態聯立方程組求解得到時，識別誤差較大。可能的原因有兩個：(1)2階模態的振型識別有較大誤差；(2)擬合參數q1過程中產生的誤差較大。

注：圖中橫坐標軸以最左端1號傳感器測點為坐標原點，向右為正方向，單位為m。圖17 各階模態振型Fig.17 Curves of each order modal vibration shape

從以上結果可知，本方法在進行一次試驗的情況下可得到多個索力值，在確定所測拉索索力值時，可將偏離其他大多數索力值的結果去掉，再求索力平均值，本試驗所得平均值如表11所示。

表11 修正后索力識別結果

由表11可知，本次試驗所得索力值精度能夠滿足工程實際需要。

最后將本研究提出的測試方法與經典測試方法進行對比。由于經典測試方法涉及到拉索的計算長度及抗彎剛度的選取，因此計算長度分別取拉索全長、拉索無套筒段長度、1階模態的π/q1，抗彎剛度分別取每根鋼絲抗彎剛度的代數和、將鋼束視為實體進行計算所得EI。

采用1階頻率作基頻代入經典理論公式進行索力計算，兩類經典索力測試方法計算結果見表12。

表12 經典索力法識別結果

由表11及表12可知，計算長度的選取不慎引起的索力測試誤差巨大；對于梁模型，實際抗彎剛度的取值范圍巨大，EI的選取引起的索力測試誤差不容忽視。本研究方法測得的抗彎剛度為3 715.48 kN·m2，介于鋼絲實體與獨立體代數和之間，相對來說更接近于視拉索為實體的計算所得。

本研究的測試方法能夠同時避免計算長度與抗彎剛度的選取問題，提高了索力測試的精度。

5 結論

本研究通過推導整理梁單元索力計算公式，采用有限元模擬短索，研究了短索索力測試方法，并進行了索力測試數值模擬與實驗室拉索索力測試，得到了如下結論：

(1)在梁模型理論的基礎上整理得到一個適用于一般邊界條件的索力計算公式，并指出兩端鉸接邊界條件下的索力計算公式為梁模型新公式的一種特殊形式。

(2)結合隨機子空間法及曲線擬合技術推出了一種基于模態分析且未知拉索抗彎剛度的前提下，能夠適用于一般邊界條件的短索索力識別方法，并分析了其適用范圍及測試誤差可能的來源。

(3)通過索力測試數值模擬與實驗室拉索索力測試試驗，驗證了短索索力測試方法的可行性與適用性，索力識別精度能夠滿足工程需要。