考慮行人舒適度的空間纜索懸索橋車致振動控制

唐茂林，王 鵬，2，李翠娟

(1.西南交通大學 土木工程學院，四川 成都 610031;2.長江勘測規劃設計研究有限責任公司，湖北 武漢 430010)

0 引言

高速地鐵通過橋梁時，對結構的作用是隨時間變化的周期性荷載，在某特定軌道不平順譜影響下，可能使荷載激勵頻率與結構自振頻率一致，引起結構共振。共振導致結構產生較大的動力響應，影響橋上行人舒適度，此時有必要對結構進行振動控制。許海亮[1]研究了路面不平整度激勵下車路耦合振動，得出路面不平整度越差路面產生的振動位移也越大；Den Hartog[2]首次提出了STMD系統在結構受到簡諧力作用下的最優參數求解方法；Han[3]等利用阻尼比相同、調諧頻率等間隔分布的MTMD系統有效控制了結構振動；李春祥[4-5]對MTMD進行了大量動力分析，得出MTMD系統具有更好的有效性和魯棒性；樊健生[6]研究發現人-橋共振時采用MTMD將比單個TMD具有更高的減振效率；王文熙[7]研究了TMD系統在自身參數偏離下的減振有效性和可靠性問題,并給出增強TMD系統有效性和可靠性的一些建議。張鐸等[8]基于移動簡諧荷載列模型，研究了地鐵過橋時，諧振頻率、荷載列移速等對共振效應的影響；肖新標等[9]研究了TMD對不同速度簡諧荷載激勵下橋梁動力響應的控制效果；郭文華[10]等提出TMD可有效抑制高速鐵路簡支箱梁的共振效應；王浩等[11]研究了TMD對南京長江大橋車致振動豎向加速度的控制效果；靖仕元[12]對長沙磁浮工程道岔梁，采用多重調諧質量調諧阻尼器(TMD)的方式控制一定激振頻率帶的振動，達到控制頻率能全覆蓋；徐家云[13]研究得出TMD能夠較好地減小重載鐵路橋梁的振動響應。已有車致振動控制方面的研究大都是基于鐵路簡支梁或者連續梁橋，對帶有人行道的大跨度空間纜索懸索橋車致振動方面的研究較少。

目前一些城市市政橋梁不僅承受地鐵軌道交通，還布置有人行道，對于這類橋梁，地鐵過橋時振動問題突出，有必要對其行人走行舒適度進行研究。本研究以某座跨度為(45+330+60) m的市政軌道交通懸索橋為背景，依據表1中德國EN03[14]規范規定的采用峰值加速度作為評價準則，研究地鐵荷載作用下橋上行人的走行舒適度。該橋邊跨為平行纜，主跨為外張式空間纜，吊索間距為7.5 m，主梁采用桁架與箱梁的組合梁，在橋塔處連續通過，上層橋面承受雙向地鐵荷載，下層橋面布置有6 m寬的人行道。該橋實際設計中，兩岸橋塔塔頂橫向間距并不相同，矮塔側塔頂I.P點橫向間距為43 m，高塔側塔頂I.P點橫向間距為47.4 m，吊索下吊點橫向間距34.4 m。

表1 EN03規定的舒適度等級(單位：m/s2)

1 橋梁結構振動分析

懸索橋具有強烈的非線性[15]，導致結構的響應與外載荷激勵的變化不成比例。懸索橋的車橋振動分析為瞬態非線性分析，因此在ANSYS中建立結構三維有限元模型如圖1所示。其中采用link10單元模擬吊桿和主纜，采用beam4單元模擬主塔和主梁，考慮車輛激勵在ANSYS進行瞬態非線性時程分析。

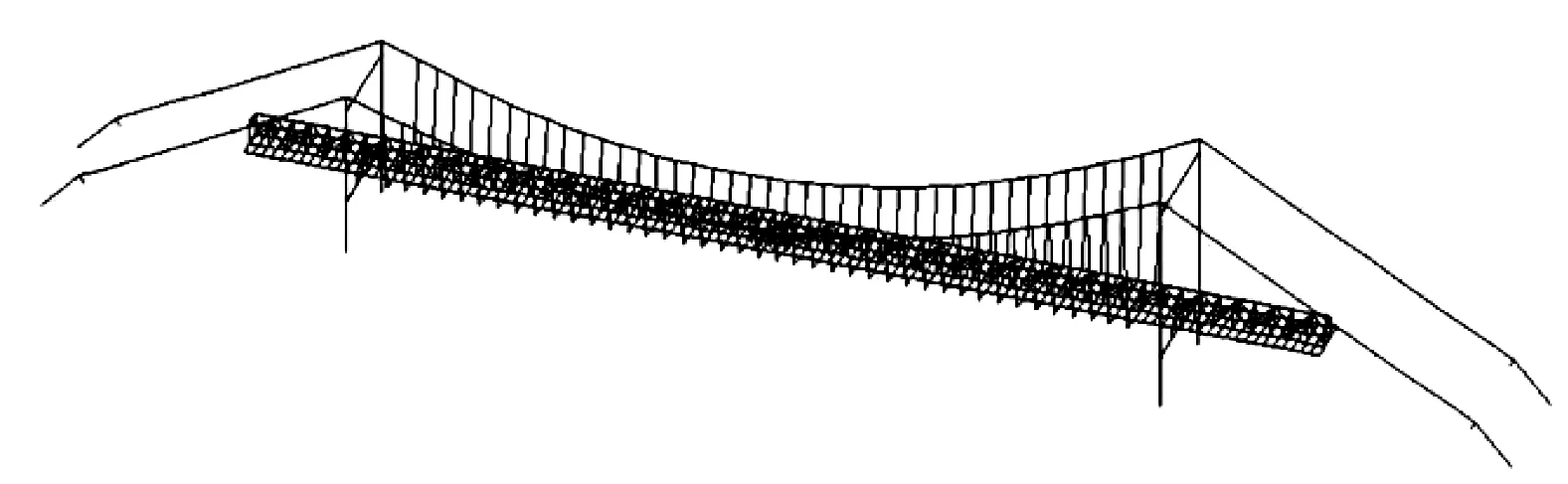
圖1 有限元模型Fig.1 Finite element model

1.1 動力特性分析

動力特性是橋梁全局動態剛度指標的重要體現，是橋梁動力分析的基礎。橋梁結構的動力特性主要包括結構的振型、自振頻率、模態質量等，本研究主要研究在地鐵激勵下該橋的豎向振動，表2展示了該橋前三階豎彎振型的關鍵參數。

表2 主要振型自振頻率Tab.2 Natural frequencies of main modes

1.2 考慮軌道不平順的車致振動分析

地鐵車輛作用主要由軌道不平順引起的簡諧荷載和常量的軸重荷載疊加而成。地鐵激勵的簡諧荷載幅值近似取為[8]P=0.2·Po=32 kN，地鐵主軸重Po=160 kN，則實際車輛荷載即可等效為圖2中按特定間距排列的簡諧荷載。該橋設計地鐵為由6輛車編組的A型地鐵，圖中只示意了3輛，地鐵激勵大小為：

P(t)=160+32×sin(ωt)。

(1)

確定荷載模式以后，在該橋上下游加載相向而行的兩列簡諧地鐵荷載列，模擬地鐵在橋上會車，諧振頻率分別與該橋的一階和三階豎彎模態頻率相同，由于二階豎彎模態質量不大，并不能激發結構共振，此處不做研究。圖3～圖4為移動簡諧荷載列作用下，主跨330 m范圍內主梁位移和加速度時程變化圖，從圖中數據可以看出，在列車荷載激勵下，結構分別被激發了一階和三階豎彎共振，且一階豎彎模態頻率簡諧荷載列激勵下，結構的位移和加速度響應都要比三階頻率簡諧荷載作用下的響應大。結構被激發一階豎彎共振時，主梁最大位移值為-0.393 m，最大加速度值為1.122 m/s2，行人走行舒適度等級為“不舒適”；激發三階豎彎共振時，主梁最大位移響應為-0.224 m，最大加速度響應為0.492 m/s2，行人走行舒適度處于“很舒適”等級。

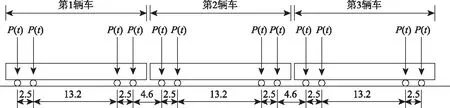
圖2 地鐵簡諧荷載(單位:kN)Fig.2 Simple harmonic load of subway(unit:kN)

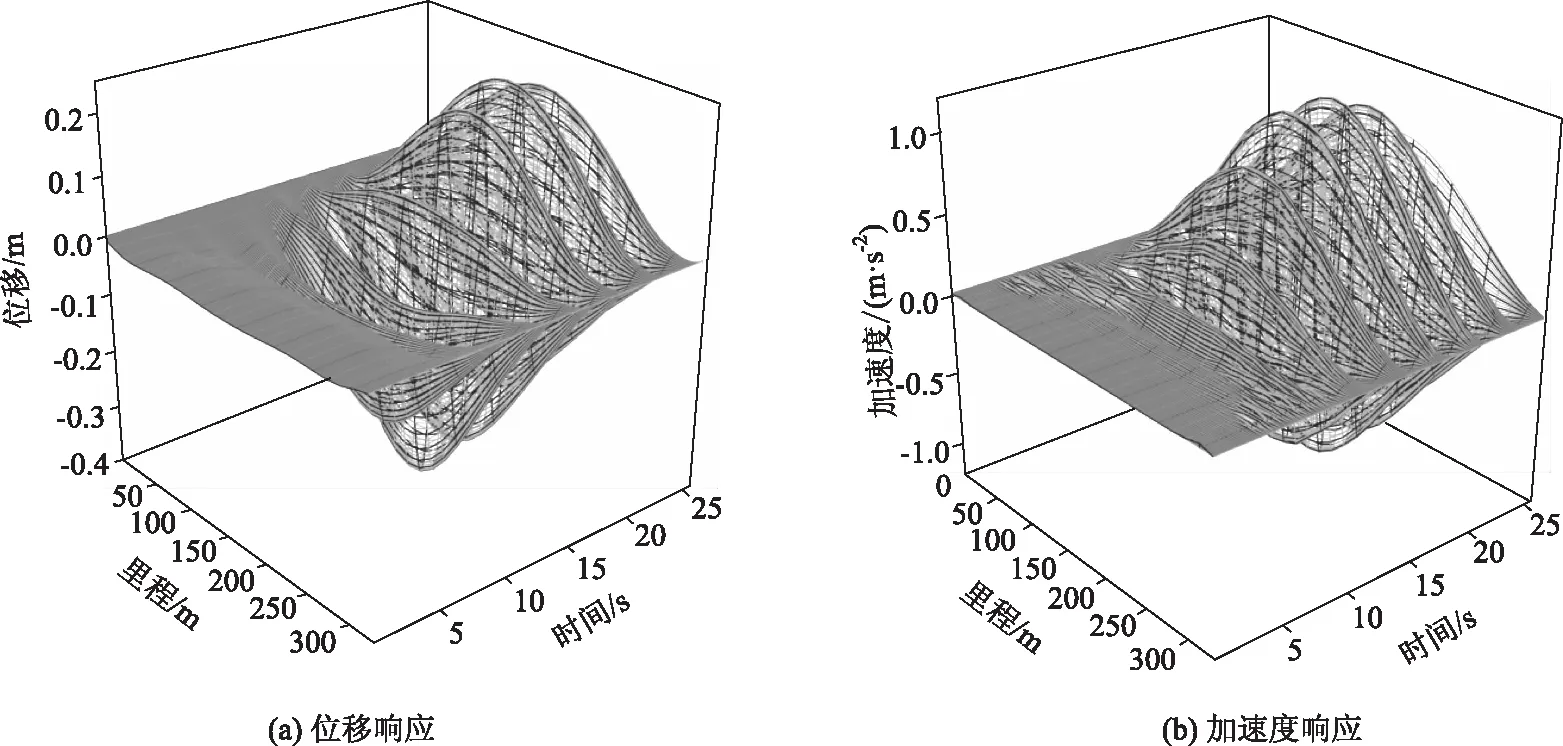
圖3 一階豎彎頻率簡諧荷載下結構響應Fig.3 Structural responses under first-order vertical bending frequency harmonic loading

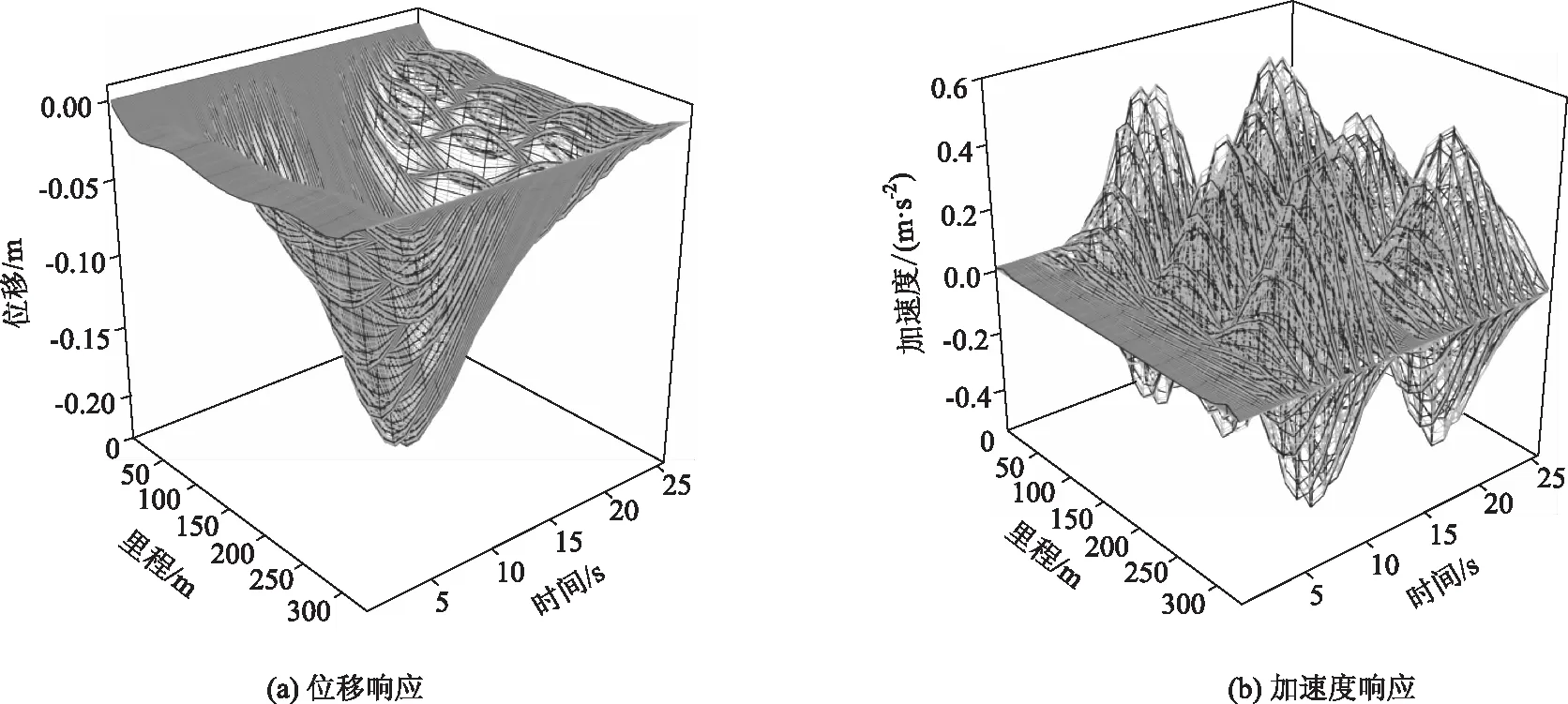
圖4 三階豎彎頻率簡諧荷載下結構響應Fig.4 Structural responses under third-order vertical bending frequency harmonic loading

2 基于TMD的結構振動控制

上一節研究發現，當軌道不平順的諧振頻率與一階豎彎模態頻率相同時，行人走行舒適度處于“不舒適”等級，采用TMD對主梁振動進行控制是有必要的。

2.1 抑振原理

待控結構簡化為質量矩陣只有一個自由度的質量塊Mp;結構阻尼系數為Cp;剛度系數為Kp;在待控結構上裝置TMD系統進行振動控制。單調諧頻率質量阻尼器(STMD)系統只有單個子TMD；多調諧頻率質量阻尼器(MTMD)系統具有多個子TMD，子TMD的自振頻率以結構被控模態頻率為中心，按一定的間隔對稱分布。每一個子TMD都由一個質量為mi的質量塊、一個剛度系數為ki的彈簧以及一個阻尼系數為ci的線彈性阻尼器組成。根據子TMD頻率特點可以發現，STMD系統只能對一個頻率點進行控制，而MTMD系統則能對一個小的頻率段進行控制。該橋利用STMD與MTMD系統進行振動控制的力學模型如圖5、圖6所示。在主梁振幅響應最大區域安裝N個子TMD，每個子TMD質量、剛度和阻尼矩陣分別為mi，ki，ci。可以把主梁運動微分方程寫成如下非矩陣形式：

(2)

式中，yp(x,t)為主梁在車輛激勵下各點的位移;P(t)為所計入軌道不平順影響后的地鐵激勵。假設第i個子TMD的位移響應為yi(x,t)，可以得出如下第i個TMD的受力平衡方程式：

(i=1, 2,…,n)。

(3)

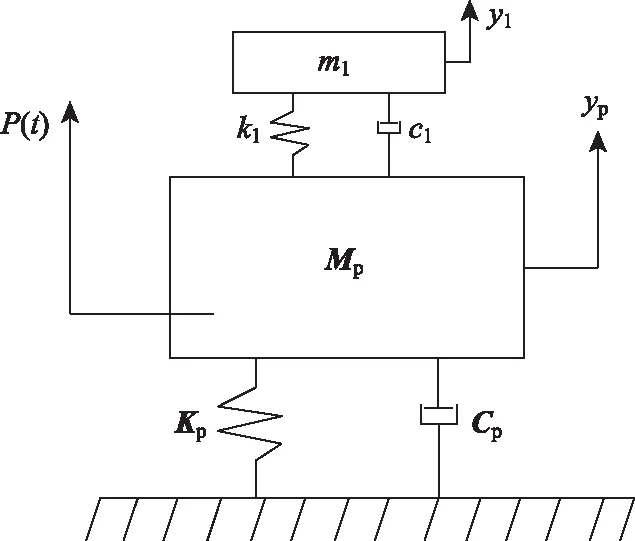
圖5 STMD力學模型 Fig.5 Mechanical model of STMD

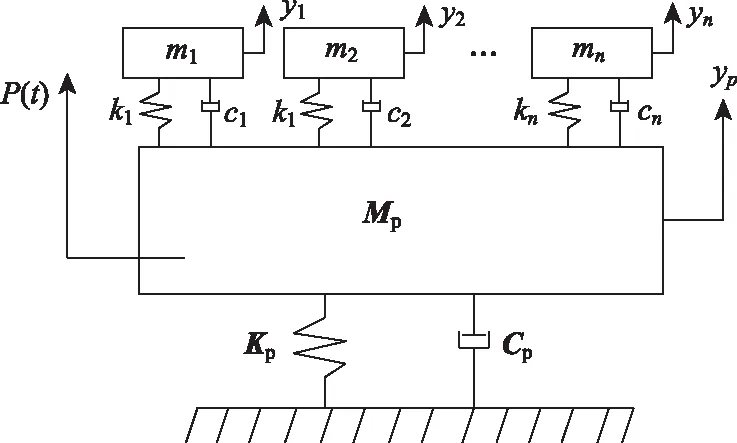
圖6 MTMD力學模型Fig.6 Mechanical model of MTMD

2.2 參數確定

采用Den Hartog最佳參數確定方法[2]確定TMD最優參數，其中最優頻率比:

(4)

最優阻尼比:

(5)

TMD主要物理參數:

fTMD=f·αopt，

(6)

(7)

cTMD=2mTMD·ωTMD·εopt，

(8)

式中,f為主結構待控振型自振頻率；μ為阻尼器質量與結構模態質量之比;ω為角頻率。

此處考慮到恒載撓度，STMD系統質量比μ取0.02。依據以上方法，得出針對該橋一階豎彎模態振動控制的STMD系統主要參數如表3所示。

表3 STMD系統設計參數

文獻[4-5]介紹了MTMD主要參數的計算方法，其中平均頻率為：

(9)

第j個子TMD的頻率為：

(10)

頻率間隔為:

(11)

調諧頻率系數:

(12)

則每個子TMD的調頻系數:

(13)

總質量比:

(14)

平均阻尼比系數:

(15)

式中,ωs為橋梁結構的自振頻率;ms為對應模態下的模態質量，調諧頻率系數與平均阻尼比可由公式(4)～(5)計算得到。一個TMD系統有n個子TMD，ωj為第j個子TMD的角頻率；ω1為第1個TMD的角頻率；mj為第j個子TMD的質量;εj為第j個子TMD的阻尼比。

由等量分析原則，此處MTMD系統總質量比也取0.02、最優頻率間隔取0.16，采用5個質量與阻尼比相同，阻尼系數與剛度系數不同的子TMD對結構進行振動控制。依據上述方法，計算針對該橋一階豎彎振動控制的MTMD系統參數如表4所示。

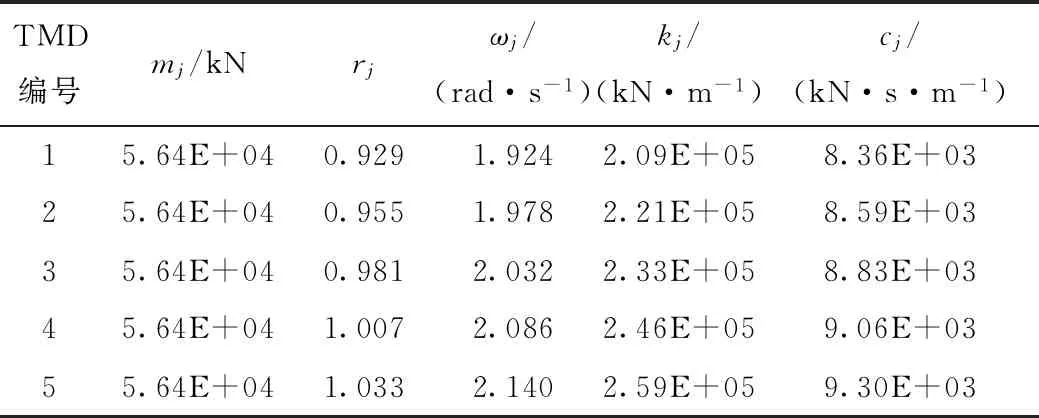
表4 MTMD系統設計參數表

2.3 振動控制分析

在有限元模型中采用mass21單元模擬阻尼器的質量，采用combin14單元模擬阻尼器的彈簧剛度和阻尼剛度，并將mass21單元與結構聯系在一起。已有研究表明，在滿足空間要求的情況下，盡可能的把TMD布置在主梁動力響應最大的位置，其抑振效果最好[16]。如圖7所示，可以在桁架下層橋面跨中5片下橫梁中間預設節點板，將整個TMD系統裝配在圖中位置，最大限度減小結構振動。

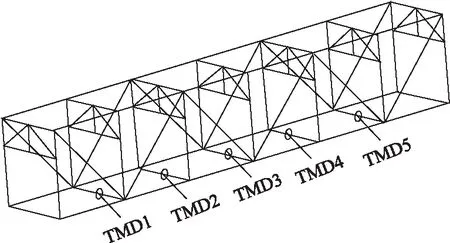
圖7 TMD系統在主梁上的布置圖Fig.7 Layout of TMD system on main girder

本研究主要針對一階振動進行控制，將表3、表4設計的STMD與MTMD系統布置在上述主梁跨中位置。圖8為雙向地鐵過橋時，兩類系統控制下跨中主梁位移、加速度時程曲線。從中可以看出STMD系統控制下結構最大加速度為0.751 m/s2，有效降低了33.2%；MTMD系統控制下結構最大加速度為0.712 m/s2，有效降低了36.6%。兩類系統都實行人舒適度進入“中度舒適”等級，對比分析結果可以發現，MTMD系統具有更好的抑振效果。

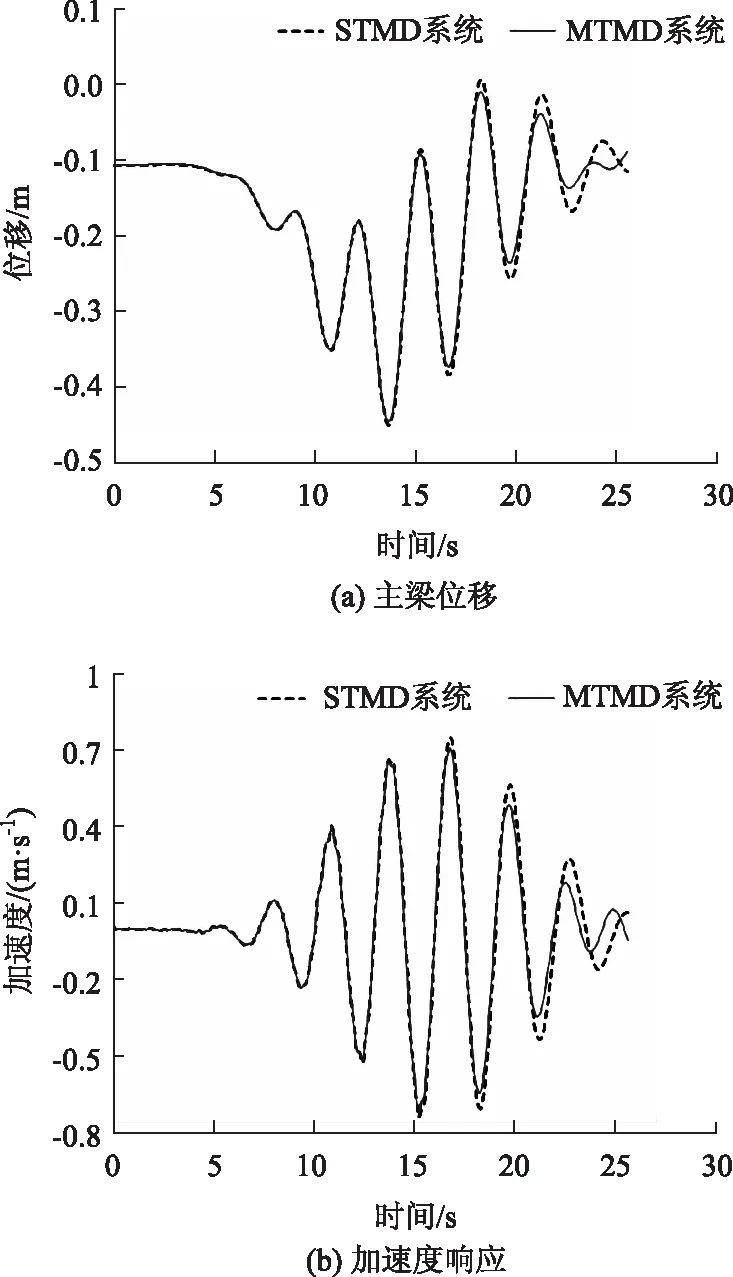
圖8 跨中主梁位移、加速度響應時程曲線Fig.8 Time-history curves of displacement and acceleration response of main girder at midspan

2.4 參數敏感性分析

TMD在加工制造時存在加工誤差，可能引起自身參數與設計值不相符，影響抑振效果[17]。此處對STMD、MTMD系統的子TMD主要參數存在誤差時的抑振能力進行研究，結果可作為TMD參數優化設計的依據，也可對分析TMD制造誤差影響抑振效果提供參考。在表3、表4設計參數的基礎上，分別讓質量、剛度、阻尼參數按下述3種狀態發生偏移。

狀態1：在剛度和阻尼保持不變的情況下，各子TMD質量按其設計參數的0.7，0.85，1.15，1.3倍發生改變；

狀態2：在質量和阻尼保持不變的情況下，各子TMD剛度按其設計參數的0.7，0.85，1.15，1.3倍發生改變；

狀態3：在質量和剛度保持不變的情況下，各子TMD阻尼按其設計參數的0.7，0.85，1.15，1.3倍發生偏改變。

圖9繪出了跨中加速度響應極值隨著子TMD質量、剛度、阻尼發生偏移時的變化情況。從中可以看出：子TMD質量發生偏移時，系統的抑振效果會下降；剛度增加15%獲得更好的抑振效果，此時STMD與MTMD系統控制下結構最大加速度為0.731，0.681 m/s2，分別降低了34.8%，39.3%；隨著子TMD阻尼的增加，系統的減振效率呈單調下降趨勢，但影響不明顯。

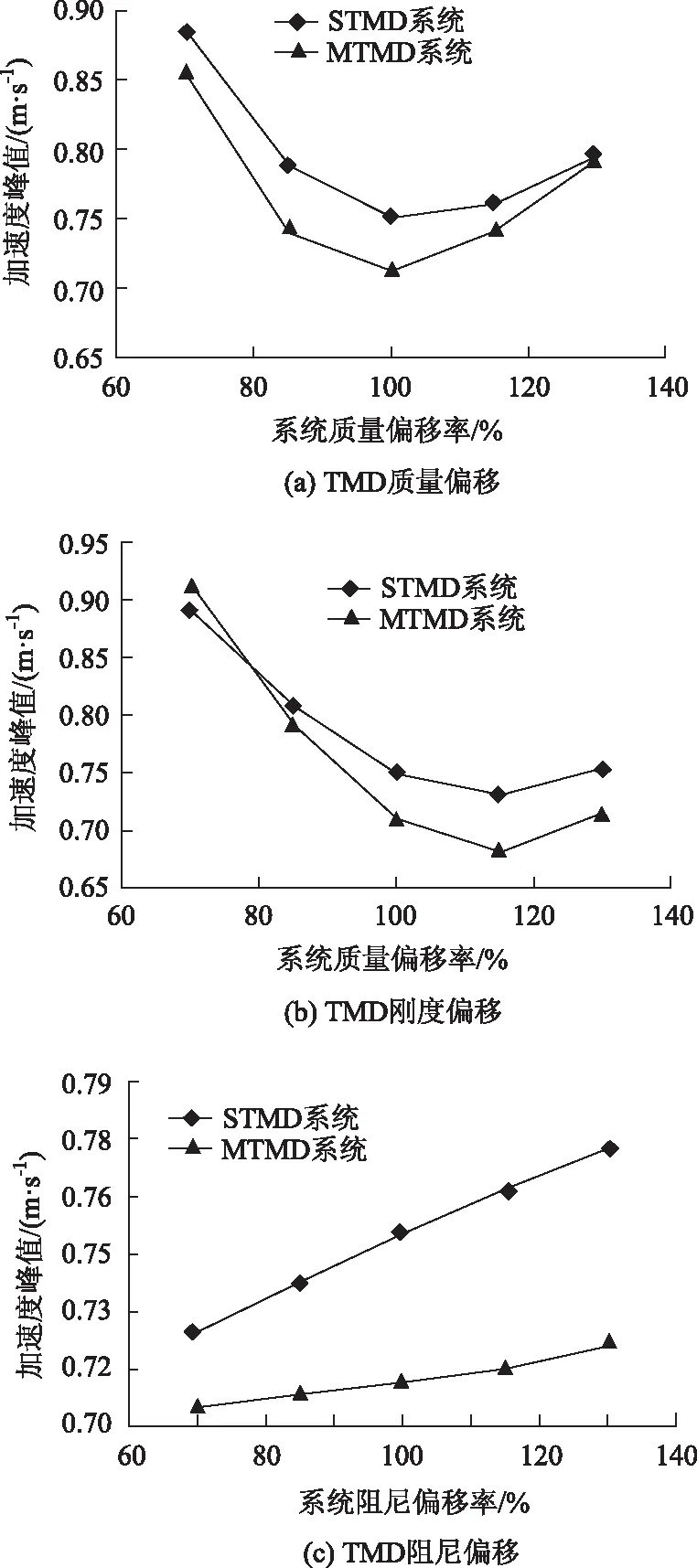
圖9 加速度峰值隨TMD偏移變化曲線Fig.9 Curves of acceleration maximum value vs. deviation of TMD

3 魯棒性分析

3.1 結構自身頻率變化的魯棒性分析

橋梁在運營期間，結構可能產生收縮徐變[18]，建筑材料也可能存在老化現象，導致結構實際自振頻率與TMD設計時所采用的并不一致，進一步對STMD與MTMD系統的抑振效果帶來影響。為實現結構自振頻率改變，本研究將該橋跨矢比由8.5修改為9.5，結構一階豎彎模態頻率降到1.95 rad/s，進而研究抑振系統在結構自身頻率改變后的魯棒性能。表5列出了頻率變化后，雙向地鐵激勵下兩類系統的抑振效果，從中可以發現，MTMD系統依舊具有較高的有效率，跨中加速度減小了32.4%，STMD系統減小了29.7%。由此可見，MTMD抑振系統具有更好的魯棒性，能更長久保障橋上行人舒適度。

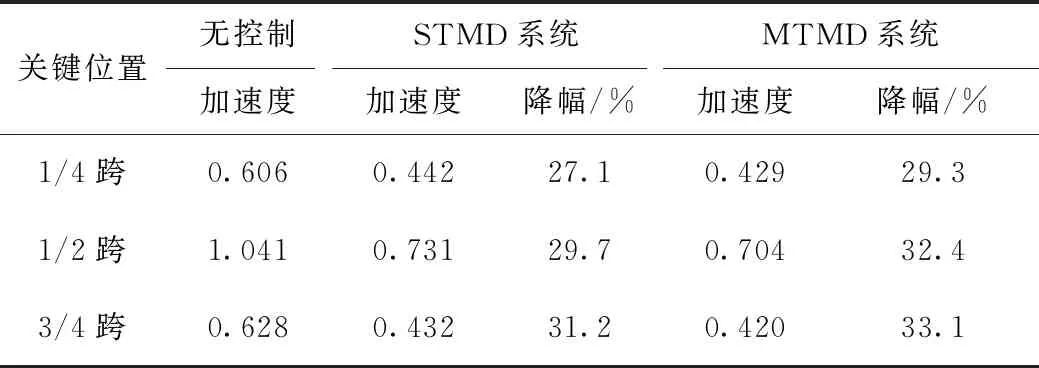
表5 不同模型加速度響應極值(單位：m/s2)

3.2 TMD個數對抑振系統魯棒性的影響

保證質量比為2%不變的前提下，分別將13個，9個，5個，1個子TMD裝置原橋主梁跨中，研究MTMD系統魯棒性隨子TMD個數的變化情況。隨著子TMD個數的減少，單個子TMD的質量與體積也將增加。采用9個子TMD時，可以考慮將子TMD布置在下橫梁與下弦桿交點處的節點板，同一個下橫梁與兩片桁架的節點處就可以布置兩個子TMD；采用13個子TMD時，可以同時將子TMD布置在下橫梁與兩片桁架的節點以及下橫梁中間的節點，同一個下橫梁上就可以布置3個子TMD。這樣盡可能的將TMD布置在橋梁跨中附近，可使TMD系統發揮更好的抑振效果。

分析過程中，激勵荷載選用前文介紹的地鐵模型，模擬雙向地鐵在橋上會車，地鐵諧振頻率為1.87 rad/s。作用地鐵激勵頻率與該橋一階豎彎模態頻率2.07 rad/s偏移時，各類MTMD系統的加速度響應如圖10所示，從中可以發現，主梁的加速度響應極值隨著TMD個數的增加有所下降，但幅度逐漸減弱，趨于平緩。因此，適當的增加TMD個數，可以有效解決激勵荷載頻率改變對橋上行人舒適度帶來的影響。

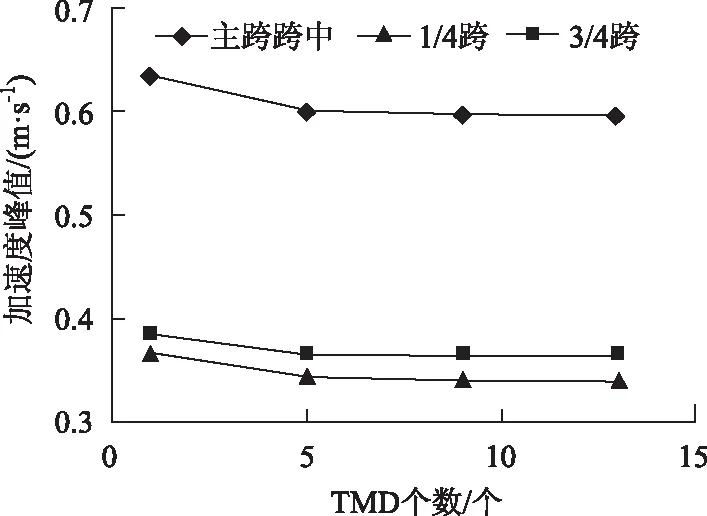
圖10 加速度峰值隨TMD個數變化曲線Fig.10 Curves of acceleration maximum value vs. number of TMD

4 結論

本研究依托某市政軌道交通空間纜索體系懸索橋，以橋上行人走行舒適度為出發點，對該結構在考慮軌道不平順影響的簡諧地鐵荷載激勵下的動力響應進行分析，并分別研究了調諧質量阻尼器STMD以及MTMD系統對結構的抑振效果。本研究主要結論如下：

(1)該橋一階豎彎振型模態質量較大，當軌道不平順的諧振頻率接近該模態頻率時，容易激發結構共振，引起橋上行人走行不適。

(2)無阻尼器時，跨中加速度響應極值為1.122 m/s2；STMD系統控制下結構最大加速度為0.731 m/s2，有效降低了34.8%；MTMD系統控制下結構最大加速度為0.681 m/s2，有效降低了39.3%。添加阻尼器使橋上行人舒適度從“不舒適”進入“中度舒適”。

(3)結構自身頻率發生改變時，MTMD系統也能較好地控制結構振動，魯棒性良好；另外，隨著TMD個數的增加，MTMD系統的魯棒性進一步提高。