體驗思路突破，探究問題解法

唐曉霞

[摘? 要] 開展二次函數綜合題探究可以強化學生知識，提升學生能力. 教學中建議以問題為依托，使學生體驗思路突破的過程，開展解法拓展，歸納解題策略，讓學生感悟類型問題的解法異同. 文章以一道二次函數綜合題為例，開展解法探究，與讀者交流.

[關鍵詞] 二次函數;動點;幾何;面積;矩形

■ 問題呈現

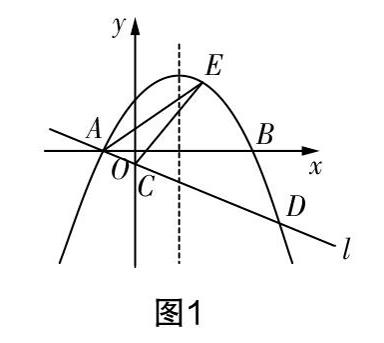
問題?如圖1，在平面直角坐標系xOy中，已知拋物線y=ax2-2ax-3a（a<0）與x軸相交于點A和點B（點A在點B的左側），直線l經過點A并與y軸的負半軸交于點C，與拋物線的另一交點為D，且CD=4AC，試回答下列問題.

（1）求點A的坐標以及直線l的函數表達式.

（2）設點E是直線l上方拋物線上的一個動點，連接AE，EC. 若△ACE面積的最大值為■，試求a的值.

（3）設點P為拋物線對稱軸上一點，點Q位于拋物線上，試分析以A，D，P，Q四點為頂點的四邊形能否為矩形. 若能，請求出點P的坐標;若不能，請說明理由.

■ 思路突破

問題中的三個小問較為典型，下面逐問探究.

（1）拋物線的解析式的每一項均含有參數a，對解析式變形后可得y=a（x-3）（x+1），結合交點與解析式的關系可知拋物線與x軸的交點分別為（-1，0），（3，0），即A（-1，0），B（3，0）. 可將直線l的函數表達式設為y=kx+b，求其表達式只需求出k，b的值即可. 題干條件給出CD=4AC，可聯想相似比進行坐標轉化求解.

直線l經過點A，則有0=-k+b，即b=k，則直線l的函數表達式可簡化為y=kx+k. 因為CD=4AC，所以點D的橫坐標為4，縱坐標為5k，即點D的坐標為（4，5k）. 又點D在拋物線上，將其坐標代入拋物線解析式，可解得k=a，所以直線l的函數表達式為y=ax+a.

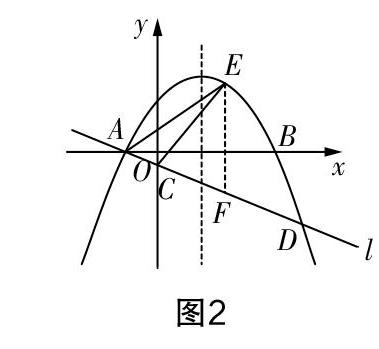
（2）該問設定點E為拋物線上一動點，屬于二次函數中的面積最值問題. 可設出點E的坐標，采用面積割補法構建△ACE的面積模型，將問題轉化為二次函數最值問題，從而確定a的值.

如圖2，設點E的坐標為（x，ax2-2ax-3a），過點E作y軸的平行線，與直線l交于點F，則點F的坐標為（x，ax+a）. 計算可得EF=ax2-3ax-4a，又S■=S■-S■，代入線段長，化簡后可得S■=■ax-■2-■a. 分析可知，當x=■時，△ACE的面積取得最大值-■a，則-■a=■，解得a=-■.

（3）該問分析以A，D，P，Q為頂點的四邊形能否為矩形，基本策略是“假設→論證”. 分析時需要利用矩形的性質，由邊的垂直來提取其中的直角三角形，利用勾股定理建立線段長的關系. 分析可知，AD可以為矩形的一條邊，也可以為矩形的一條對角線，因此需要進行分類討論.

聯立直線l與拋物線的解析式，得ax2-2ax-3a=ax+a，解得x1=-1，x2=4，所以D（4，5a）. 由拋物線的解析式可知其對稱軸為直線x=1，因為點P在拋物線的對稱軸上，所以可設P（1，m）. 下面分兩種情形進行討論.

①若AD為矩形的一條邊，如圖3，則點Q的坐標為（-4，21a），m=21a+5a=26a，則P（1，26a）. 因為四邊形ADPQ為矩形，所以∠ADP=90°. 在△ADP中使用勾股定理，有AD2+PD2=AP2，代入線段長可得25+（5a）2+（1-4）2+（26a-5a）2=4+（26a）2，解得a =-■，所以此時點P的坐標為1，-■.

②若AD為矩形的一條對角線，如圖4，由點A和點D的坐標，可推知AD的中點為■，■a，點Q的坐標為（2，-3a），則m=5a-（-3a）=8a. 所以P（1，8a）. 因為四邊形AQDP為矩形，所以∠APD=90°. 在△ADP中使用勾股定理，有AP2+PD2=AD2，代入線段長可得4+（8a）2+（1-4）2+（8a-5a）2=25+（5a）2，解得a=-■，此時點P的坐標為（1，-4）.

綜上可知，以A，D，P，Q四點為頂點的四邊形能成為矩形，此時點P的坐標為1，-■或（1，-4）.

■ 方法拓展

上述對一道二次函數綜合題進行了解讀與突破，其中第（2）問和第（3）問屬于綜合性極強的問題，聯系了幾何知識，其構建思路具有一定的參考價值，兩問均屬于二次函數中的經典問題，其解析策略靈活多樣，下面深入探討.

1. 面積最值問題策略

二次函數中的面積最值問題一般分兩步進行突破：第一步，建模——建立關于幾何面積的模型;第二步，代數分析——可利用函數性質、不等式性質. 上述第（2）問采用了面積割補法構建模型，但僅是將三角形轉化為兩個簡潔的圖形，從過程來看，還需求解兩個三角形的面積. 對于該類問題，還可以采用面積鉛垂法，即添加與坐標軸平行的輔助線，將其轉化為兩個共底三角形，于是簡化面積模型.

例1? （2019年海南中考改編）如圖5，A（-5，0）和B（-4，-3）是拋物線y=ax2-bx+5上的兩點，拋物線與x軸的另一交點為C.

（1）試求拋物線的解析式;

（2）點P是拋物線上不與點B和點C相重合的動點，設點P的橫坐標為m，當點P在直線BC下方運動時，試求△PBC面積的最大值.

解析?（1）利用點A和點B的坐標可求得拋物線的解析式為y=x2+6x+5.

（2）由拋物線的解析式可求得點C的坐標為（-1，0）. 過點P作y軸的平行線，與直線BC的交點設為Q，則△PBC的面積可以表示為S△PBC=■·PQ·xC-xB. 易知點P的坐標為（m，m2+6m+5），可推知Q（m，m+1），所以PQ=-m2-5m-4. 所以S△PBC=■（-m2-5m-4）=-■m+■2+■. 分析可知，當m=-■時，△PBC的面積取得最大值■.

2. 矩形存在性問題策略

二次函數中的矩形存在性問題需要充分利用矩形的特性，上述第（3）問結合勾股定理來構建解析方程，其核心是矩形對角線分割出的直角三角形，采用的是代數論證. 該類問題還可以利用矩形的對角線相等且平分來解析，其中的平分關系可聯系中點坐標.

例2?如圖6，已知矩形OABC的頂點A（-3，0），過點C的直線y=-2x+4與x軸交于點D，二次函數y=-■x2+bx+c經過點B和點C.

（1）試求二次函數的解析式.

（2）若點P為CD的中點，分析二次函數上是否存在點M，使得以A，P，C，M為頂點的四邊形為矩形. 若存在，請求出點M的坐標;若不存在，請說明理由.

解析? （1）從函數圖像關系可求得二次函數的解析式為y=-■x2-■x+4.

（2）連接AC和MP，設交點為E. 假設四邊形APCM為矩形，則點E為AC和MP的中點. 由A（-3，0）和C（0，4）可知AC=5，E-■，2. 由C（0，4）和D（2，0）可知P（1，2）. 由中點坐標公式可得點M的坐標為（-4，2）. 于是只需確保點M的坐標滿足二次函數的解析式，即可論證四邊形APCM為矩形的假設成立. 將x=-4代入y=-■x2-■x+4中，可解得y=2，所以存在點M（-4，2）使得以A，P，C，M為頂點的四邊形為矩形.