帶抗風夾的直立鎖邊屋面系統抗風性能的參數研究

孫 瑛 ，武 濤 ，武 岳

(1.哈爾濱工業大學土木工程學院，黑龍江，哈爾濱 150090;2.哈爾濱工業大學結構工程災變與控制教育部重點實驗室，黑龍江，哈爾濱 150090)

直立鎖邊屋面系統是將相鄰屋面板的卷邊借助專用設備與T型支座依次咬合，然后連接到支承結構的屋面系統。憑借其優良的防水性能、抗變形能力以及多樣化的板面形式得到了越來越多設計者的喜愛，因此被廣泛應用于大跨建筑的屋面圍護結構中。由于直立鎖邊屋面系統在咬合處的抗風承載能力較低，在臺風影響區等風力較大的地區，該類屋面系統在強風作用下的風揭破壞事故時有發生，如圖1所示。

圖1 直立鎖邊金屬屋面系統風揭破壞事故Fig.1 Wind uplift accident of standing seam roof system

Schroter[1]與Sinno[2]分別通過空氣靜壓試驗與空氣動力學試驗研究了直立鎖邊屋面系統的受力性能，確定了相應型號屋面系統抗風承載能力。Damatty等[3]與Ali和Senseny[4]分別用彈簧單元與接觸單元模擬屋面連接接縫建立直立鎖邊屋面系統的有限元模型。其中Damatty等[3]通過施加靜力荷載得到了屋面系統的抗風承載力，而Ali和Senseny[4]通過動力分析得到阻尼對夾子反力的影響不大。通過一系列的試驗與模擬研究，國外已提出關于屋面系統抗風揭的標準試驗方法[5_6]，并且已經得到了很多國家的認可。需要指出，國外的直立鎖邊屋面系統在形式和構造細節上與國內的直立鎖邊屋面系統存在較大的差異，所取得的研究成果無法直接用于國內的直立鎖邊屋面系統設計中。國內學者則多數集中于屋面板的抗風承載力的研究，秦國鵬等[7]與孫成疆[8]基于美國FM4471標準，借助空氣壓力箱對直立鎖邊屋面系統驗開展了抗風揭試驗屋面系統的抗風承載力，同時指出鎖縫是該類型屋面系統的薄弱環節。考慮到屋面型號眾多，國內學者同時進行了數值模擬研究，陳玉[9]借助有限元分析軟件對屋面系統的受力性能、破壞形式、承載力、變形等響應開展了參數研究，并擬合得到了承載力計算公式。盡管開展了大量試驗與數值研究，仍未阻止風揭破壞事故的發生。為此國內學者們[10]設計了抗風夾用來加強鎖縫處的咬合作用，但在目前的多數研究中并沒有考慮抗風夾的影響。

為研究帶抗風夾的直立鎖邊屋面系統在風荷載下的受力性能，使用沙袋進行靜力堆載試驗，并借助有限元軟件ANSYS進行靜力荷載下帶抗風夾的直立鎖邊屋面系統的參數模擬研究，確定了屋面系統的破壞準則，通過分析不同型號屋面系統的破壞形式、承載力、變形及應力變化特點，提出了直立鎖邊屋面系統的承載力計算公式，為工程中需要采用抗風夾進行局部加強時的設計提供參考。

1 靜力試驗研究

1.1 靜力試驗介紹

試驗中使用沙袋對屋面系統進行反向靜力加載，每次加載將9個或18個沙袋(分別對應0.25 kPa或0.5kPa)均勻平鋪在屋面系統上，持壓1 min后進行下一次加載，直至屋面系統破壞。試驗加載裝置如圖2所示，其中立柱、鋼梁和檁條均采用I20a鋼。設計時，檁條兩端腹板均進行了延伸，使其可以與鋼梁腹板接觸。連接檁條與鋼梁時，借助預先加工的角鋼，采用12個M20高強螺栓將檁條與鋼梁連接。試驗時先將所有T型支座均用4個直徑5 mm的螺栓與檁條連接，然后借助專業設備將屋面板與T型支座咬合，最后將整個裝置翻轉，試驗框架長3000 mm，寬1350 mm。

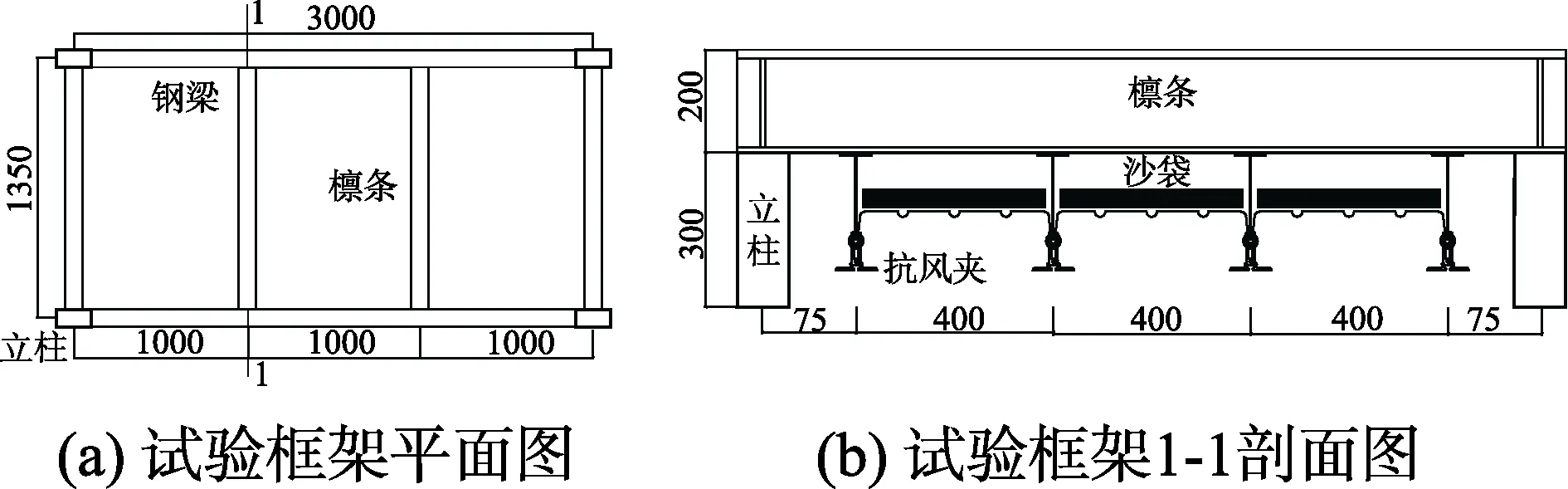
圖2 試驗加載裝置圖/mmFig.2 Experimental loading frame

試驗中使用的屋面板型號為 400/65、300/65，即板寬分別為400 mm和300 mm，豎向板高度為65 mm，厚度均為1 mm，圖3中給出了所使用的屋面板、T型支座和抗風夾的幾何信息。

試驗中采用的直立鎖邊屋面板材料為鋁鎂錳合金，型號為 3004-H36，材料的性能參數信息見表1。共進行了4組工況的靜力試驗研究，工況參數信息見表2。

試驗主要測量屋面板的變形及抗風夾處的受力情況，根據以往國內學者[7,9]的研究結果，屋面系統的豎向板及跨中屋面板應力往往較大，因此在豎向板和跨中屋面板布置應變片，同時也在抗風夾上布置了應變片。應變片采用BX120-2AA。為了測抗風夾與屋面直立鎖邊卡口的相對變形，用激光位移計進行測量，激光位移計采用KEYENCE 公司生產的LKG-400，量程為10 mm，精度為0.001 mm。圖4為使用的應變片與激光位移計，圖5給出激光位移計測點的布置示意圖，其中圖5(a)中a點與b點的橫向位移即為卡口位移。

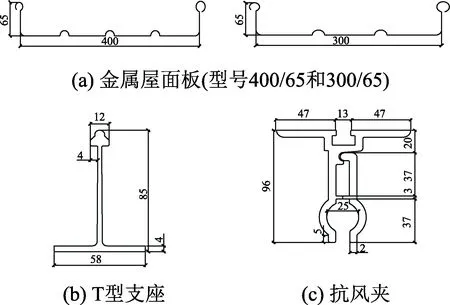
圖3 組件基本信息/mmFig.3 Component basic information

表1 屋面板材料信息Table 1 Material properties of roof plate

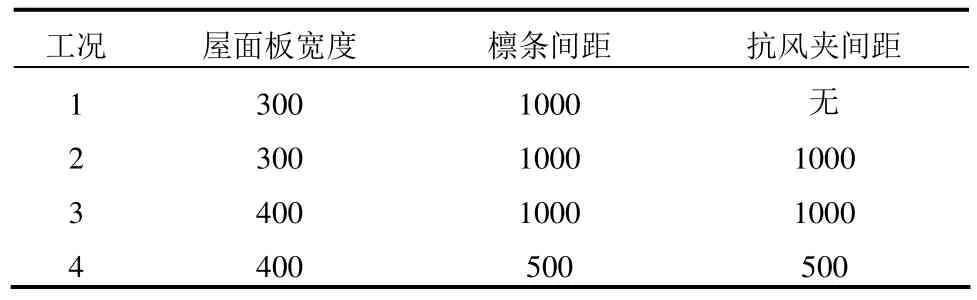
表2 試驗工況表/mmTable 2 Experimental cases

圖4 測量裝置圖Fig.4 Measuring device

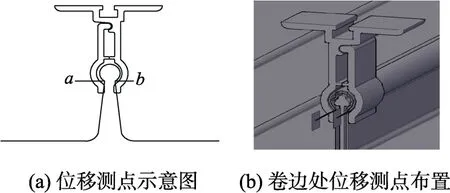
圖5 位移測點布置示意圖Fig.5 Displacement measurement point layout

1.2 試驗結果分析

在上述4組靜力加載試驗中，工況1和工況3分別在3.6 kPa和6.5 kPa時由于卡口側向位移達到1.8 mm左右而發生脫扣破壞，工況2和工況4則分別在7.9 kPa和12.5 kPa時由于屋面最大應力超過極限強度而發生撕裂破壞。

試驗表明，直立鎖邊屋面系統在荷載作用下的破壞形式主要是脫扣破壞(如圖6(a))和撕裂破壞(如圖6(b))。前者是由于卡口位移過大，T型支座對屋面卷邊的約束作用消失，屋面板脫離T型支座被掀翻，工況1和工況3正是這種破壞形式；后者是由于抗風夾對屋面豎向板橫向位移的限制，抗風夾附近豎向板發生應力集中，產生較大的應力值，工況2、工況4即發生撕裂破壞。

圖6 直立鎖邊屋面系統主要破壞形式Fig.6 Main failure modes of the standing seam roof system

取4組工況的卡口位移與豎向板最大測點應力變化曲線進行分析，如圖7和圖8所示。圖9給出了應變測點的位置。工況1和工況3分別在3.6 kPa、6.5 kPa時發生脫扣破壞，觀察此時的屋面應力分別為220 MPa、250 MPa，均低于極限強度280 MPa。而此時的卡口位移則均為1.8 mm左右，可以認為，由于卡口位移過大，T型支座的約束作用消失，引起屋面系統的脫扣破壞；工況2和工況4分別在7.9 kPa和12.5 kPa時發生撕裂破壞，此時的卡口位移僅為1 mm左右，低于發生脫扣破壞的臨界卡口位移值(1.8 mm)。觀察屋面豎板的應力發現此時的屋面最大應力均已接近 300 MPa，超過極限強度280 MPa，導致了屋面系統在豎向板處發生撕裂破壞。取屋面系統破壞前的一級荷載作為屋面系統的承載力，4組工況的承載力分別為 3.4 kPa、7.6 kPa、6.0 kPa、12.0 kPa。同時可以得出，當卡口位移達到1.8 mm左右時，T型支座對屋面系統的約束作用已消失，屋面系統將發生脫扣破壞；由于屋面板材料的極限強度為280 MPa，因此可以認為當屋面的最大應力超過280 MPa時將會發生撕裂破壞。

對試驗結果的卡口位移曲線(圖7)和豎向板測點應力曲線(圖8)進一步分析，可以發現由于工況1、工況 2和工況 3的支座間距為100 mm，大于工況4的500 mm，因此在加載初期工況1、工況2和工況3的卡口位移增長明顯快于工況4。在荷載達到2 kPa時，工況1、工況2和工況3的卡口位移均達到了1 mm左右。而隨著荷載的繼續增加，工況1由于未采用抗風夾對相鄰屋面板的卷邊處進行附加約束，卡口位移繼續快速增長，在達到1.8 mm后發生脫扣破壞。工況3雖然使用了抗風夾，但由于其板寬(400 mm)較大，單個抗風夾承受的荷載增加。因此隨著荷載增加，工況3的卡口位移也繼續快速增長，同樣在達到1.8 mm后引起了脫扣破壞。工況2由于使用了抗風夾，并且板寬(300 mm)較小，這使得工況2在卷邊處的約束作用相較于工況1和工況3有很大的提升。工況2在2 kPa的荷載作用下卡口位移達到1 mm后繼續施加荷載，由于卷邊處較強的約束作用，卡口位移并未快速增長，而是緩慢增長維持在1 mm左右。工況4對抗風夾密度進行了加密，卷邊處的約束作用因此十分明顯，在整個加載過程中卡口位移均增長緩慢并最終維持在 1 mm左右。從屋面應力來看，在 2 kPa之前，4組工況的屋面應力增長比較一致。在此之后，工況1和工況3由于在卷邊處的約束作用弱，在荷載繼續增加的過程中屋面產生了較大的變形，屋面最大應力也隨之快速增加，在破壞時刻分別達到220 MPa與250 MPa。工況2和工況4由于卷邊處的約束作用強，在隨后的加載中屋面變形相對較小，屋面最大應力增加也相對較慢，隨著應力增加超過極限強度接近300 MPa，屋面發生撕裂破壞。

由試驗結果可知抗風夾的受力很小，基本不超過100 MPa，跨中屋面板的應力也多處于彈性階段，應力值不超過200 MPa。

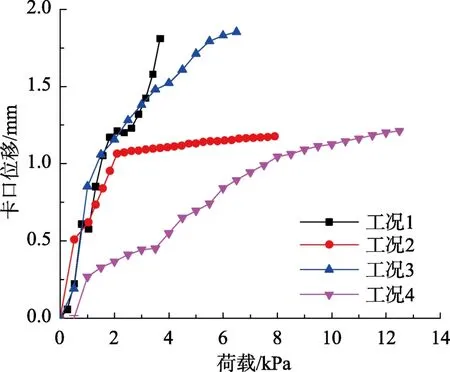
圖7 卡口位移曲線Fig.7 Seam displacement curves

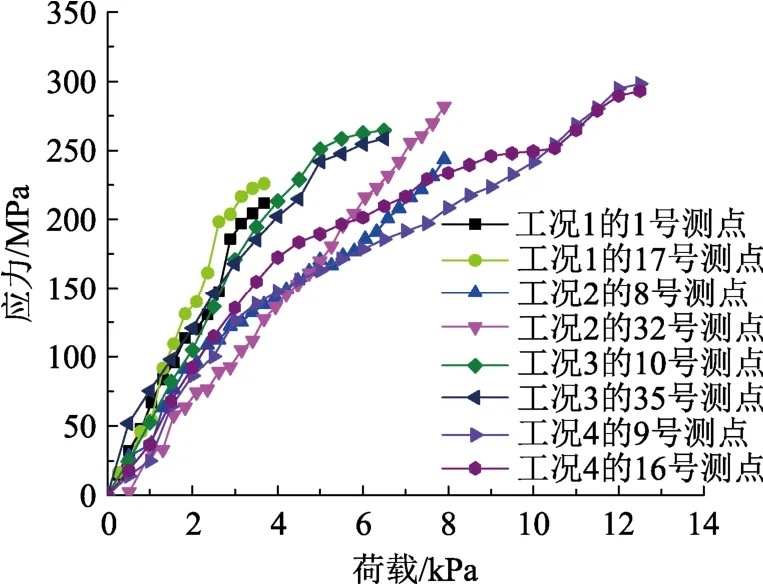
圖8 豎向板應力曲線Fig.8 Stress curves at vertical plate

圖9 豎向板處應變測試點布置圖Fig.9 Strain measuring points layout at vertical plate

2 數值模擬研究

2.1 數值模擬方法概況

直立鎖邊屋面系統型號眾多，逐一進行靜力加載試驗會消耗大量人力和財力。所以借助有限元分析軟件 ANSYS開展工況補充分析。屋面板的材性同前。屋面板使用Shell181單元，T型支座和抗風夾使用Solid187單元，另通過指定線的分段數，對屋面系統進行映射網格劃分，有限元模型見圖10。

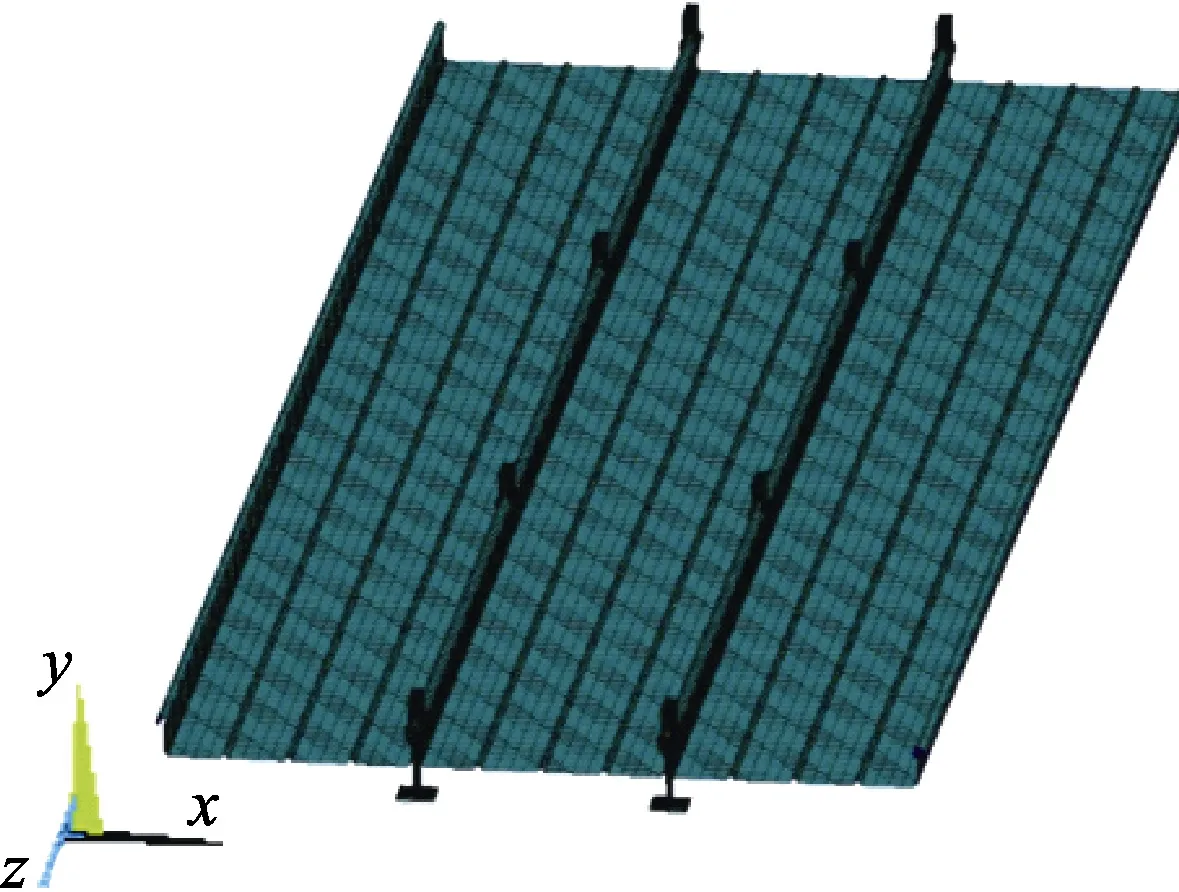
圖10 屋面系統有限元模型Fig.10 Finite element model of roof system

有限元模型兩側的z向邊界條件設定為固結，x向邊界不做約束，T型支座底部同樣設置為固結。相鄰屋面板在卷邊處相互咬合，在此處同時有T型支座的頂緊作用和抗風夾的限制作用，約束條件比較復雜。參考文獻[3_4]，采用耦合、法向約束及接觸單元模擬卷邊處的約束作用，如圖11所示。在建立上述有限元模型時，忽略下部檁條的影響，并且假定采用耦合、法向約束的卷邊不產生相對位移。

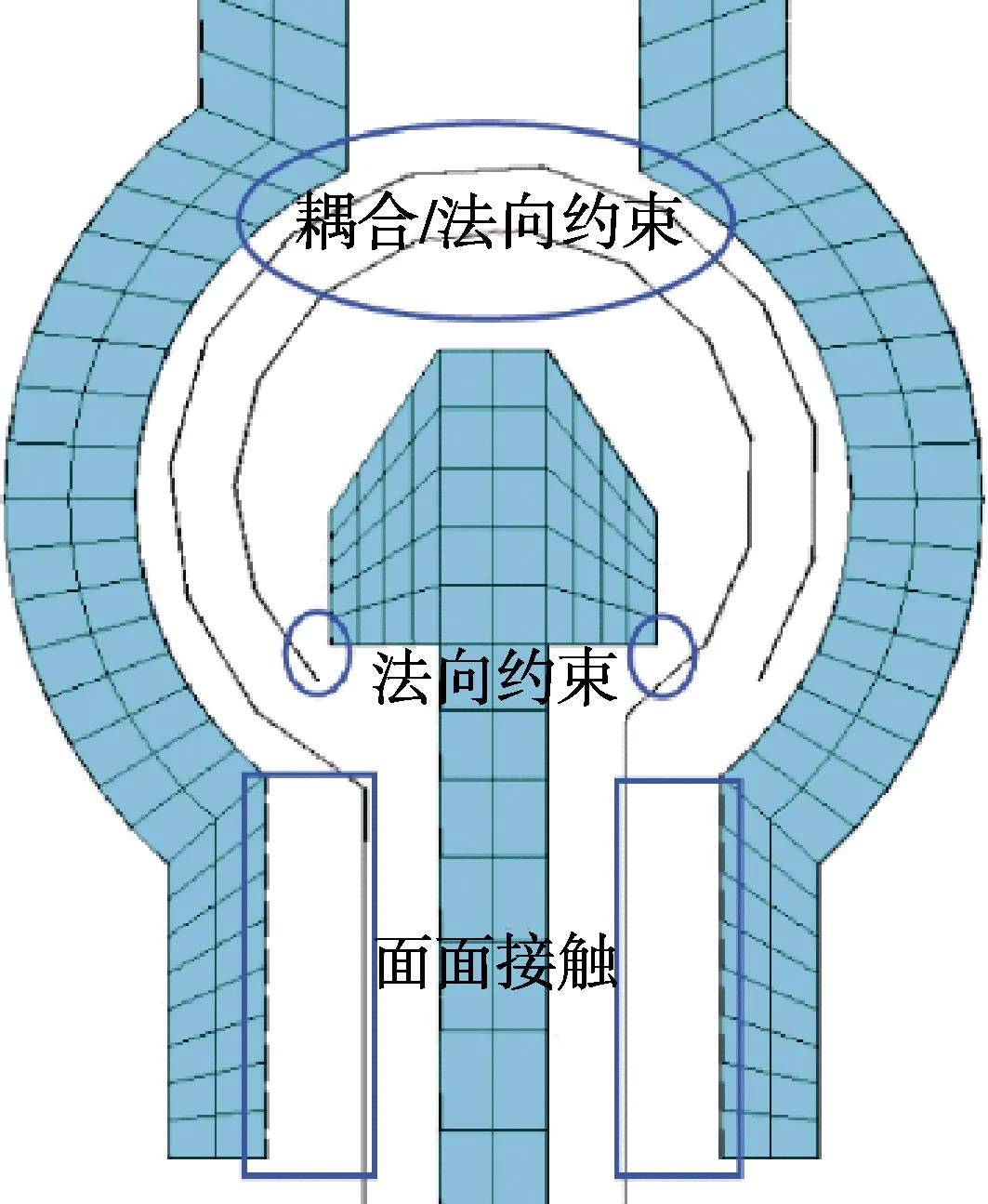
圖11 屋面系統卷邊處約束設置Fig.11 Constraint setting at the seaming of roof system

參考上述模擬方法對 32組屋面系統建立有限元模型，進行了數值模擬研究。

2.2 數值模擬方法有效性的驗證

為驗證上述數值模擬方法的有效性，將模擬工況3(板寬400 mm、厚1 mm，抗風夾間距1000 mm)的模擬結果與試驗工況3的結果進行了對比。根據試驗中布置的豎向板、屋面板跨中、抗風夾測點，選取有限元模型中相近區域的單元節點，繪制荷載-應力曲線進行對比。對比結果如圖12所示，可以發現模擬中屋面系統的極限承載力是5.4 kPa，試驗中為6.0 kPa，極限承載力僅相差0.6 kPa。卡口位移方面，破壞時刻模擬與試驗的卡口位移結果均在1.8 mm左右，且在加載過程中相差也較小，最大誤差僅為0.15 mm，不足10%；在應力方面，加載過程中抗風夾處應力誤差最大為6 MPa，誤差僅為 9%。豎向板和跨中屋面板應力雖然在加載初期應力值較小的情況下存在較大的誤差，但隨著荷載的增加，誤差逐漸縮小，當荷載達到2.5 kPa后，應力誤差均小于10%。從變化趨勢上看，模擬與試驗在三處的測點應力變化趨勢較為一致。由此采用本文的數值模擬方法可以較好地模擬屋面系統的受力性能，其參數分析的結果可供工程設計參考。圖13為加載過程中屋面應力與卡口位移分布云圖。

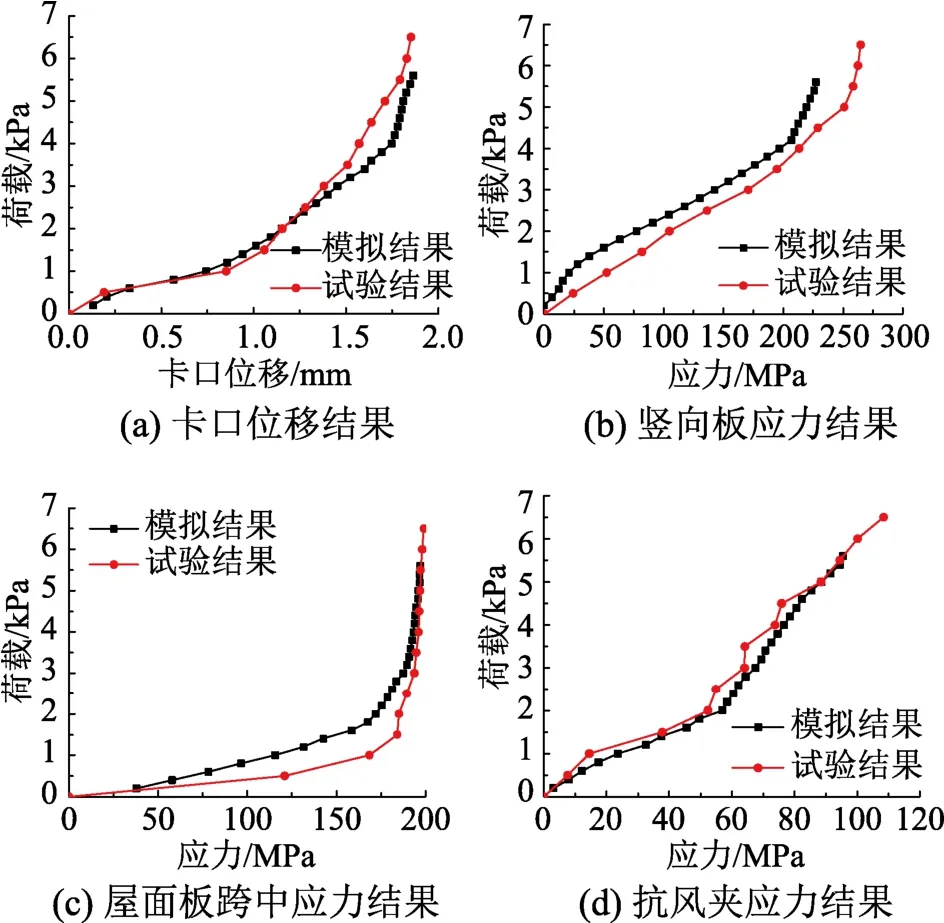
圖12 數值模擬與試驗結果對比Fig.12 Comparison between numerical simulation and experimental results

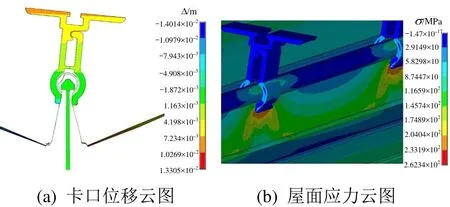
圖13 屋面系統響應分布云圖Fig.13 Response distribution of roof system

3 研究結果的參數分析

32組數值模擬工況的參數信息見表3，通過對各工況的抗風承載力、屋面最大應力和卡口位移等響應進行分析，確定板厚、板寬、抗風夾間距等參數對屋面系統受力性能的影響。同時通過討論無量綱參數與抗風承載力的相關性，確定與抗風承載力相關性最強的參數，并擬合得到承載力計算公式。

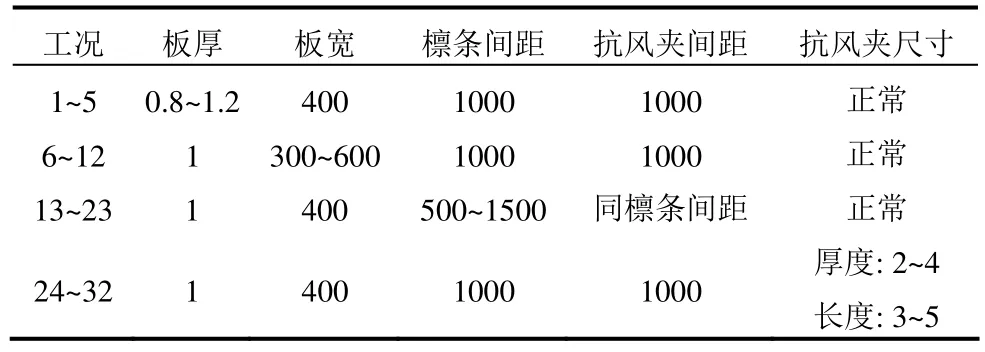
表3 數值模擬工/mmTable 3 Numerical simulation cases

3.1 屋面板厚度的影響

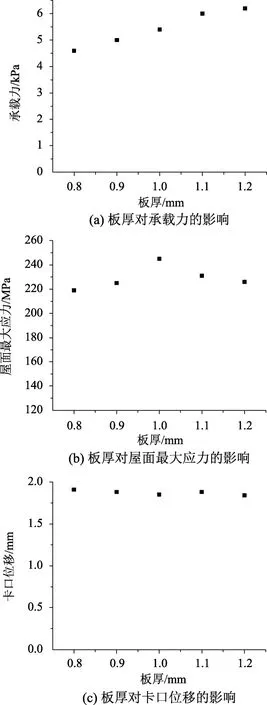
圖14 板厚的影響Fig.14 The influence of plate thickness

數值模擬工況1~工況5對屋面板厚的影響進行了研究，結果見圖14。數值模擬結果表明板厚的改變對屋面最大應力和卡口位移影響較小，5組工況均由于卡口位移達到1.8 mm而發生脫扣破壞，在破壞時刻屋面豎向板處局部最大應力均剛剛達到屈服強度，在屋面板的多數位置材料尚處于彈性階段，材料的利用率較低。當然板厚的增加使屋面板的剛度得到提升，屋面系統的抗風承載力得到一定的提高，但依靠增加板厚來提高屋面系統的承載力并不經濟。

3.2 屋面板寬度的影響

工況6~工況12研究了屋面板寬對屋面系統的影響，關鍵響應受板寬影響的變化情況見圖15，由圖15可以看出板寬的變化對屋面系統有較大的影響。板寬的增加使屋面系統的剛度降低，因而導致極限承載力由板寬 300 mm時的 7.4 kPa降低為板寬600 mm時的2 kPa，承載力降幅達到73%。同時屋面系統的破壞形式也因板寬的改變發生了轉變，在板寬300 mm與350 mm時為撕裂破壞，隨著板寬增加轉變為脫扣破壞，對應最大應力和卡口位移變化圖(見16(b)和圖16(c))上出現了明顯的改變。在撕裂破壞時，屋面應力超過了極限強度280 MPa，但卡口位移僅 1.2 mm左右。在脫口破壞時，卡口位移突增至 1.8 mm以上，而屋面應力則突降到250 MPa以下。

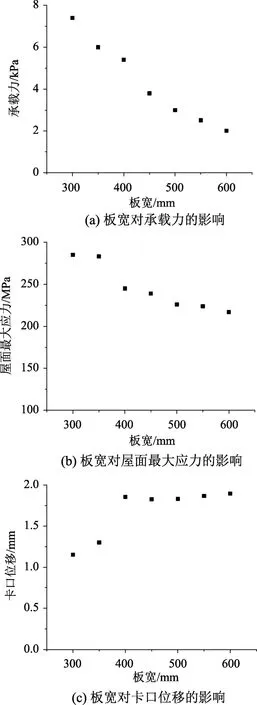
圖15 板寬的影響Fig.15 The influence of plate width

3.3 抗風夾間距的影響

數值模擬工況13~工況23針對的是抗風夾間距對屋面系統受力性能的影響，將破壞時刻各工況的響應結果整理成圖16。可以發現抗風夾間距對屋面系統的破壞形式與極限承載力均有較大影響，在抗風夾間距分別為500 mm、600 mm和700 mm時，屋面系統剛度大，產生的變形小，主要發生撕裂破壞，極限承載力均在9 kPa以上。而隨著抗風夾間距的增加，屋面系統的剛度有所下降，變形隨之加大，破壞形式也轉化為脫扣破壞，極限承載力基本在4 kPa左右。同時注意到抗風夾間距的增加，并未使屋面系統的最大應力出現較大幅度的下降，即使發生脫口破壞時，屋面最大應力也維持在245 MPa左右。

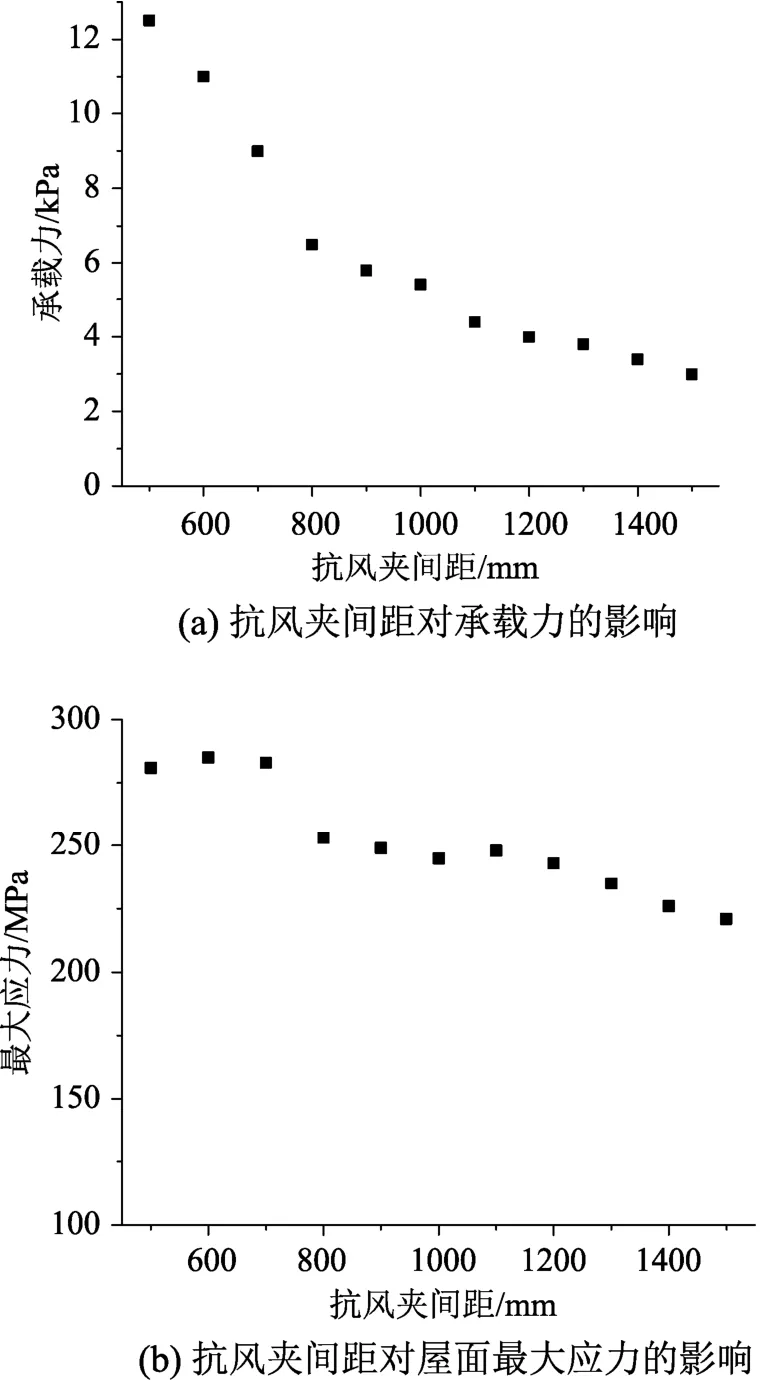
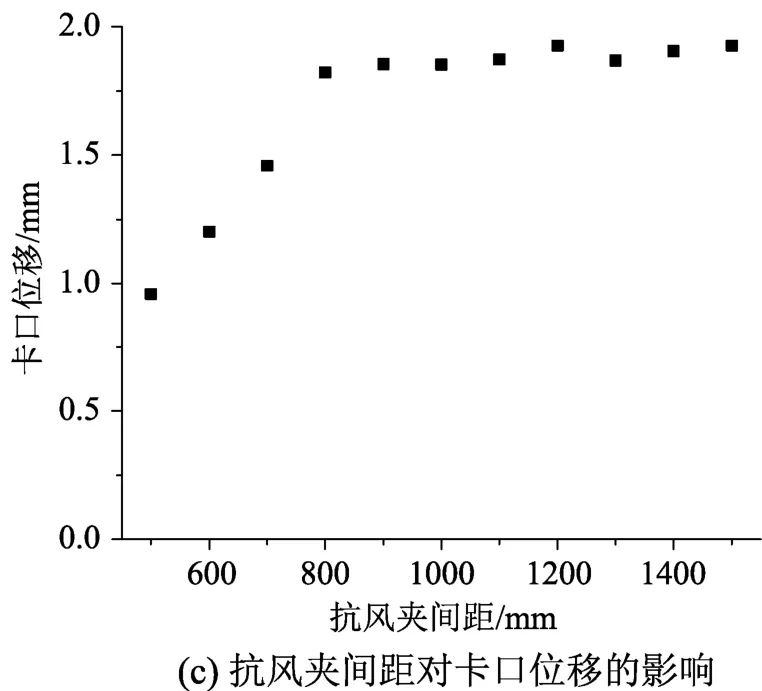
圖16 抗風夾間距的影響Fig.16 The influence of anti-wind clip spacing

3.4 抗風夾尾端厚度與長度的影響

工況24~工況32對抗風夾尺寸對屋面系統的影響進行了對比研究，相關結果匯總于表4。分析表4中數據可以發現，抗風夾尺寸的改變對屋面系統的影響有限。首先，所有模擬工況的破壞形式均為脫扣破壞。其次，各工況的極限承載力均位于4 kPa~6 kPa的荷載區間內，變化較小。最后，屋面最大應力也多集中在245 MPa左右。所以抗風夾尺寸的改變對屋面系統受力性能的影響有限。

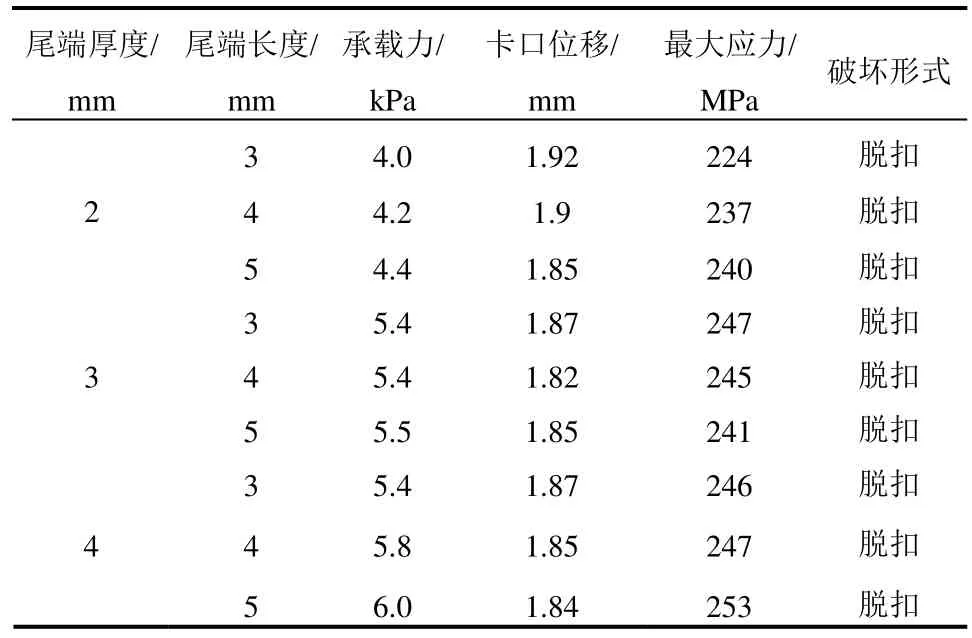
表4 抗風夾尺寸的影響Table 4 The influence of the size of the anti-wind clip

4 直立鎖邊屋面系統抗風承載力

通過前述參數分析可以發現，除抗風夾尺寸外，屋面板厚、板寬及抗風夾間距均對屋面系統的抗風承載力有較大影響，因此選擇板厚d、板寬b和抗風夾間距l作為自變量，擬合它們與抗風承載力之間的關系。

為確定板寬、板厚、抗風夾間距與屋面系統承載力的相關性，采用相關分析法對前述參數模擬結果進行統計分析，繪制各參數間的相關分析圖，相關分析圖是由每兩個參數間的相關系數構成的矩陣圖(見表5)，本文對該矩陣中的元素定義如下：

1)矩陣圖的下三角元素定義為兩參數(X1、X2)的皮爾森(Pearson)相關系數Rps，按式(1)計算。Rps是標準的線性相關系數，其絕對值越接近1則兩參數的線性關系越明顯。

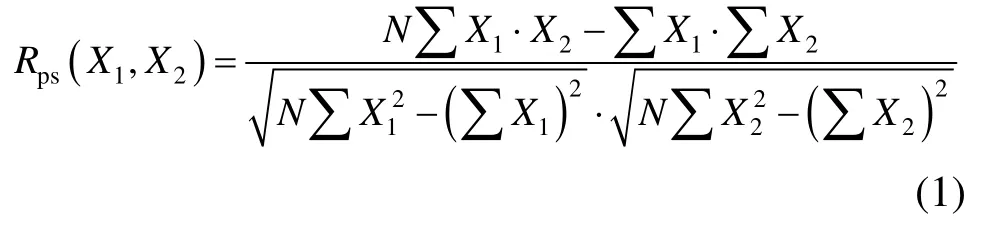
式中，N表示參數分析的工況數。

2)矩陣圖中的上三角元素定義為兩參數(X1、X2)的斯皮爾曼(Spearman)秩相關系數Rsp，按式(2)計算。Rsp不僅可以識別線性相關性，也能識別單調的非線性相關性，可用于挖掘參數間潛在的非線性函數關系。

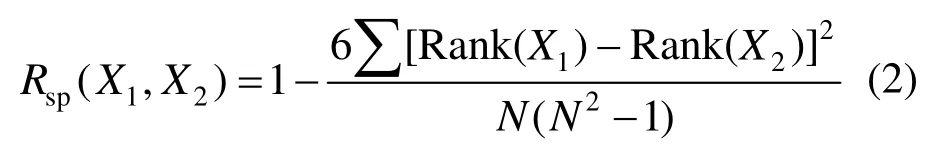
式中，Rank(·)表示取參數的秩。

本文主要關注板寬、板厚、抗風夾間距與屋面系統承載力的相關性，因此只采用上述方法計算了無量綱參數b/l、bl/d2、b/d、l/d、bd/l2與抗風承載力的相關性，相關性分析結果見表5。

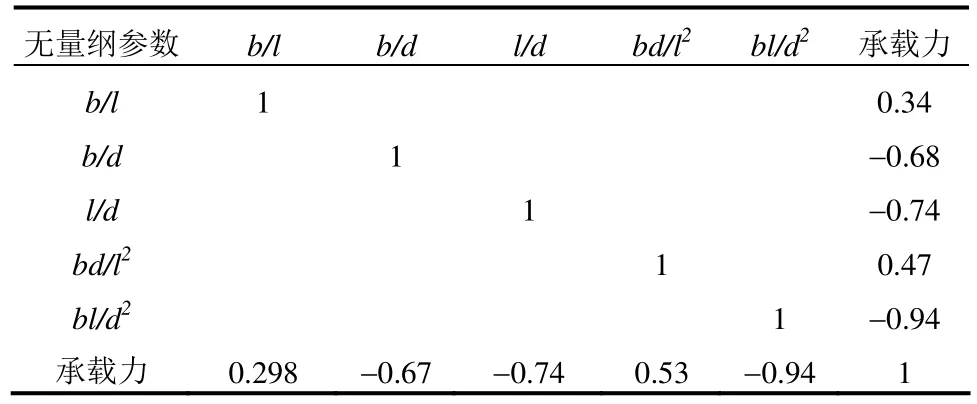
表5 不同參數對抗風承載力的相關性分析Table 5 Correlation analysis of different parameters against bearing capacity

從表5可以發現，無論是Rps還是Rsp都表明與屋面系統抗風承載力相關性最強的參數為bl/d2。然后借助MATLAB擬合該參數和抗風承載力的關系曲線，如圖17所示。同時得到了直立鎖邊屋面系統抗風承載力F的計算式(3)。需要指出，該公式主要適用于帶抗風夾的直立鎖邊屋面系統抗風承載力的預估。

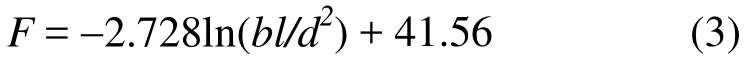
式中：F為抗風承載力，kPa；b為板寬，mm；l為抗風夾間距，mm；d為板厚，mm。

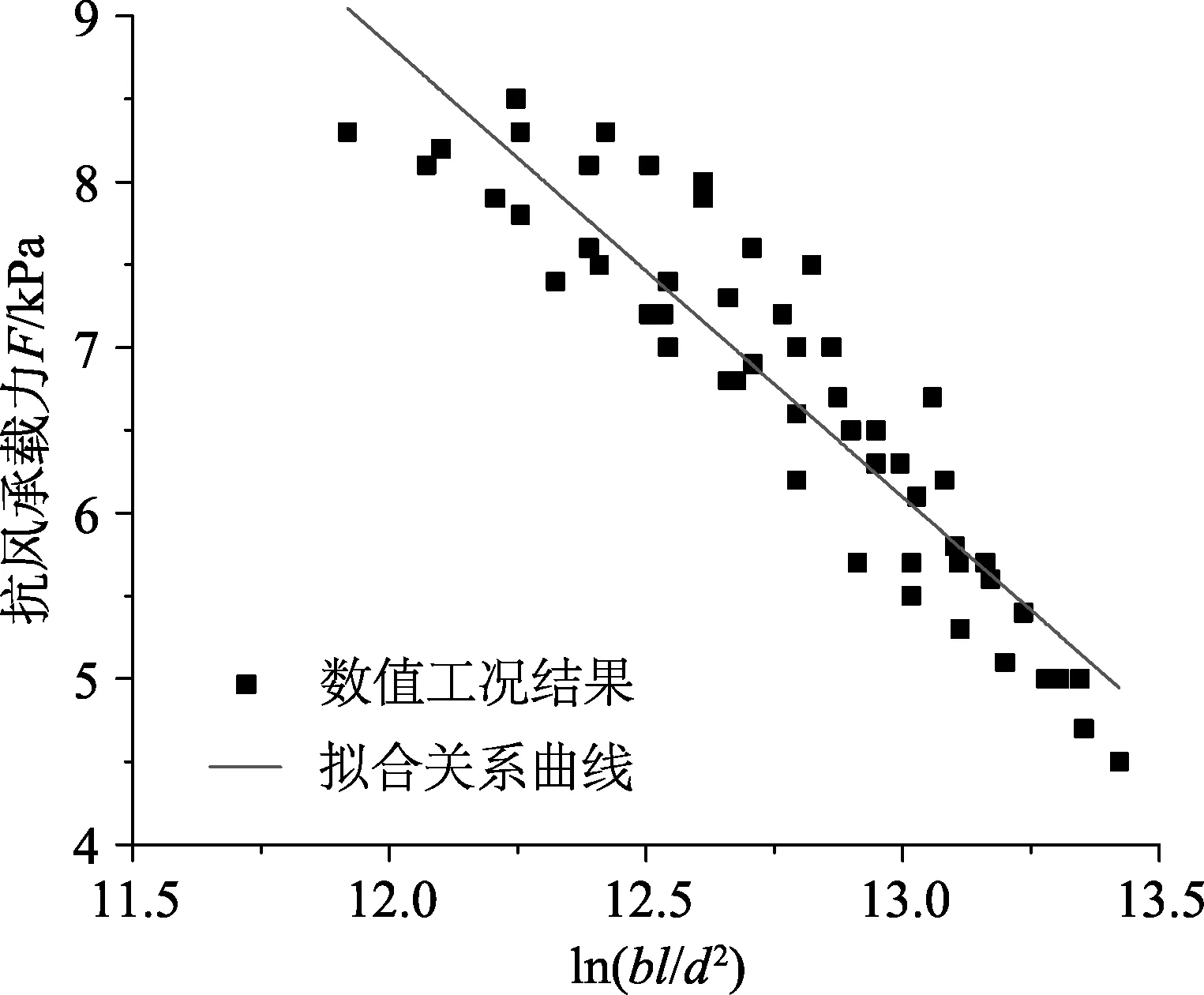
圖17 參數ln(bl/d2)與承載力F的關系曲線Fig.17 Relationship curve between ln(bl/d2)and bearing capacity F

5 結論

通過對帶抗風夾的直立鎖邊屋面系統開展的參數研究可以發現：

(1)直立鎖邊屋面系統的破壞形式主要是脫扣破壞與撕裂破壞。脫扣破壞是由于屋面卷邊處約束作用弱，荷載作用下卡口位移過大；撕裂破壞則是由于屋面卷邊處約束作用強，材料應力充分發展超過極限強度。

(2)破壞形式方面，板寬與抗風夾間距的變化會使屋面系統的破壞形式發生改變，板厚與抗風夾尺寸的變化不會影響屋面系統的破壞形式；承載力方面，板寬與抗風夾間距的變化會使屋面系統的承載力有較大幅度的改變，抗風夾尺寸對屋面承載力的影響有限，板厚的變化對屋面系統的承載力有較大影響，但也會使成本提高。

(3)通過相關性分析與數據擬合得到直立鎖邊屋面系統的抗風承載力計算公式，通過該公式可以近似得到各型號屋面系統的抗風承載力，為直立鎖邊屋面系統的抗風設計提供參考。

(4)需要指出，文中采用的靜荷載并未考慮風荷載對屋面系統的疲勞損傷影響。而長時間的風荷載作用會使屋面系統的疲勞效應更加明顯，造成屋面系統承載力、受力性能等的變化。因此在后續研究中有必要考慮真實風荷載的動力特性。