入射光照對典型光刻膠納米結構的光學散射測量影響分析*

董正瓊 趙杭 朱金龍 石雅婷?

1) (湖北工業大學, 湖北省質量工程重點實驗室, 武漢 430068)

2) (華中科技大學, 數字制造裝備與技術國家重點實驗室, 武漢 430074)

作為一種快速、低成本和非接觸的測量手段, 光學散射測量在半導體制造業中的納米結構三維形貌表征方面獲得了廣泛關注與運用.光學散射測量是一種基于模型的測量方法, 在納米結構待測參數的逆向提取過程中, 為降低參數之間的耦合性, 通常需要將結構的光學常數作為固定的已知量, 即假設結構的材料光學常數不受光學散射儀入射光照的影響.事實上, 這一假設對于半導體制造業中的絕大多數材料是成立的, 但某些感光材料的光學常數有可能隨著入射光的照射時間增加而發生改變, 而由此產生的誤差會在一定程度上傳遞給待測形貌參數的逆向提取值.本文針對聚甲基丙烯酸甲酯光刻膠薄膜培片和光柵結構分別開展了光學散射測量實驗與仿真研究, 結果表明該光刻膠材料的光學常數隨著入射光照時間增加而變化, 進而導致光柵結構形貌參數的提取結果較大地偏離于真實值, 不容被忽視.這一研究發現將為更進一步提高光刻膠納米結構三維形貌參數的測量精確度提供理論依據.

1 引 言

納米制造是指產品特征尺寸為納米量級的制造技術, 是一個國家制造水平的重要標志之一[1,2].納米制造的工藝生產質量決定了納米產業的發展前景, 而實現工藝質量監督、評估及優化的基本手段是測量.由于具有非接觸、非破壞性、低成本和易于在線集成等優點, 基于遠場光學的光學散射儀測量技術[3]除廣泛應用于納米薄膜材料的光學特性表征與膜厚測量外[4,5], 也已成為一種周期性納米結構關鍵尺寸的重要測量手段[6?10].因此, 光學散射儀也被稱為光學關鍵尺寸測量儀.

光譜橢偏儀是一種典型的光學散射儀, 其基本測量原理是通過將實際測量數據與模型仿真數據進行匹配來反演出待測納米結構參數值[11].其中,測量數據由橢偏儀探測待測納米結構的反射光或透射光而直接獲得, 根據測量數據類型的不同, 測量儀器又可分為傳統橢偏儀和Mueller矩陣偏振儀; 模型仿真數據的計算和待測參數值的反演提取則涉及到以下兩個光學散射測量理論算法：一是“正向”光學特性的建模; 二是“逆向”待測參數的提取.正向光學建模是由已知的納米結構參數、材料光學常數以及測量條件配置等, 利用電磁場理論計算出待測結構的理論數據[12]; 逆向幾何參數求取則是將實際測量數據與模型計算數據進行匹配反演得出待測參數值[13].在以計算電磁波理論為基礎的光學特性建模求解方法[12,14,15]中, 由于嚴格耦合波分析(rigorous coupled?wave analysis, RCWA)可對任意周期性結構建模, 而且具有數值求解過程比較簡單、實現相對容易、精度高等優點而得到了廣泛應用[16,17].納米結構待測參數的逆向求解主要包括庫匹配和非線性回歸這兩種方法[18], 由于前者的建庫過程相當耗時, 后者的操作過程簡單直接, 因而具有迭代收斂快速特點的列文伯格?麥夸特(Levenberg?Marquardt, LM)非線性回歸優化算法目前被廣泛應用于光學散射測量中的待測參數逆向求解[19,20].

在納米結構三維幾何形貌的逆向提取過程中,為了降低待測參數之間的耦合性, 通常需要將已知的納米結構參數、材料光學常數、入射測量條件配置等設為固定值, 而對待測的若干形貌參數進行浮動處理[6?10].考慮到納米結構測量數據的質量完全取決于測量儀器本身, 無法輕易改變, 目前已有諸多文獻通過優化入射測量條件配置以提高待測參數的測量精確度.例如, Vagos等[21]基于不確定度與靈敏度分析進行了光學特性模型及方位角的優化; Littau等[22]針對采用不同方式進行入射角范圍的選取, 從而提高了角分辨型橢偏儀的測量精度;文獻[23, 24]中分析了不同來源的系統誤差對納米結構參數測量準確度的影響, 進而優化了測量入射角和方位角; 此外, 文獻[25]中還結合全局靈敏度分析方法實現了測量方位角的優化, 提高了納米結構形貌參數的測量精度.

總體而言, 上述優化方法均是通過合理地選擇測量條件配置, 以降低測量隨機噪聲或者系統誤差對納米結構待測參數逆向提取結果的影響, 進而在一定程度上提高測量準確度或精密度.結構的材料光學常數獲取方式通常為測量同一工藝中尚未制作出形貌結構的薄膜培片, 而后在納米結構三維形貌參數的光學散射測量過程中使用測得的光學常數并假設其固定不變.這一假設對于半導體制造工業中的絕大多數材料是成立的, 但某些感光材料諸如聚甲基丙烯酸甲酯(polymethyl methacrylate,PMMA)光刻膠[26,27]可能會隨著橢偏儀入射光照射的影響而發生改變, 該誤差則可能在一定程度上傳遞給待測形貌參數的逆向提取值.為此, 本文結合實驗與仿真開展了橢偏儀入射光照對PMMA光刻膠薄膜培片和光柵結構的光學散射測量研究,以證明PMMA光刻膠光學常數隨入射光照的變化對于納米結構的光學散射測量不容忽視, 從而為更進一步提高光刻膠納米結構三維形貌參數的測量精確度提供理論依據.

2 基本原理

2.1 基于RCWA的正向光學特性建模

利用RCWA理論對周期性光柵結構進行光學特性建模的基本步驟可分為：1)由Maxwell方程組求得入射區域和透射區域的電磁場的表達式;2)對光柵區域內的介電常數及電磁場按Fourier級數展開, 并由Maxwell方程導出耦合微分方程組; 3)分別在光柵區域的上下邊界運用電磁場邊界連續條件, 通過數學求解各級衍射波的振幅, 進而計算各級衍射波的衍射效率或衍射場的強度分布等.

以圖1所示的光柵結構為例, 假設其周期為P, 占空比為f, 線高為d, 頂部線寬和底部線寬分別為DTC和DBC, 首先建立如圖1(a)所示的直角坐標系, θ為入射角, 入射波波矢k1所在的鉛垂面與xoz平面夾角為方位角φ, 電矢量E與k1所在平面的夾角為偏振角ψ.然后, 將光柵截面進行縱向分層, 則可將圖1(b)中的每個薄層等效為矩形光柵, 再將矩形光柵結構劃分為3個區域, 即區域1(入射/反射區域, z ＜ 0), 區域 2 (透射區域, z ＞ d)以及光柵區域(0 ＜ z ＜ d).區域1和區域2的復折射率分別記為n1和n2.光柵區域包含了脊部和槽部兩種介質的周期分布, 分別記其復折射率為nrd和ngr.由于本文所研究對象的材料為各向同性材料, 因此光柵區域的相對介電常數ε僅為關于x的周期性函數, 而與z無關.將光柵區域的相對介電常數展開成Fourier級數形式, 有

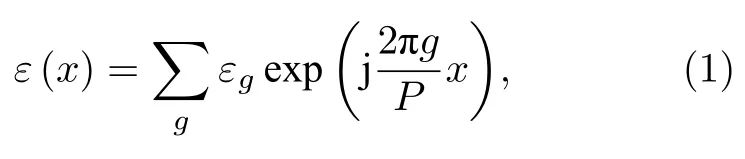
其中εg表示相對介電常數的第g級Fourier展開分量.

將入射電場的振幅歸一化后, 入射波的電場分量可表示成：

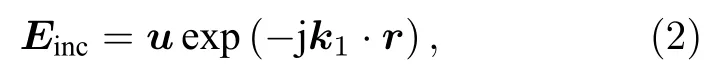
其中, u為歸一化的入射電矢量, k1表示入射波的波矢, r為平面波波面上任一點的位置矢量.

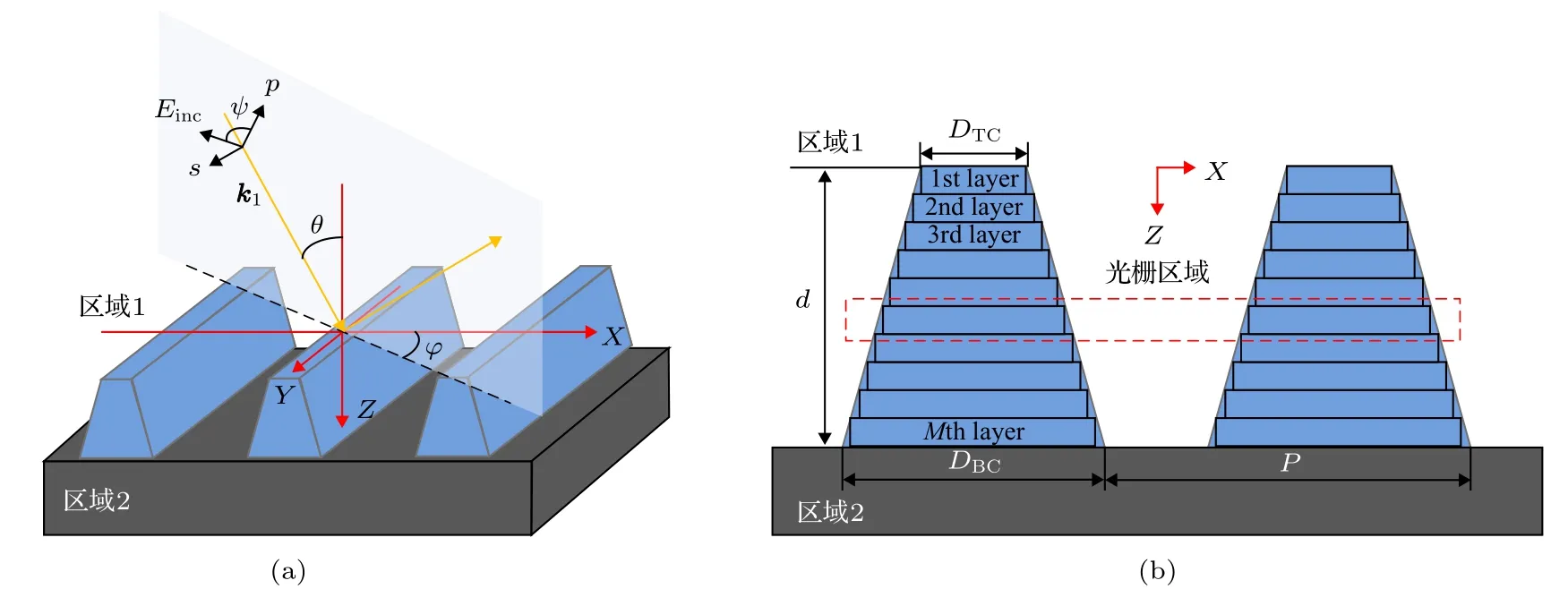
圖1 (a) 線條光柵結構的幾何形貌示意圖; (b) RCWA建模的分層示意圖Fig.1.(a) Geometry of the trapezoidal groove line grating; (b) layers division for inverse modeling based on RCWA.

由Rayleigh展開可分別得到區域1 (z ＜ 0)和區域2 (z ＞ d)電場矢量的表達式：

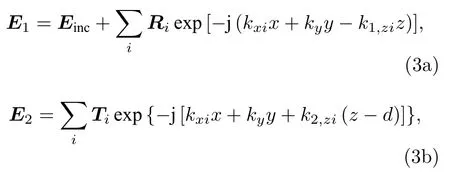
式中, Ri和Ti分別表示第i級反射波和第i級透射波的幅值矢量; kxi, ky與kl,zi分別表示第i級衍射波波矢的x, y與z分量,

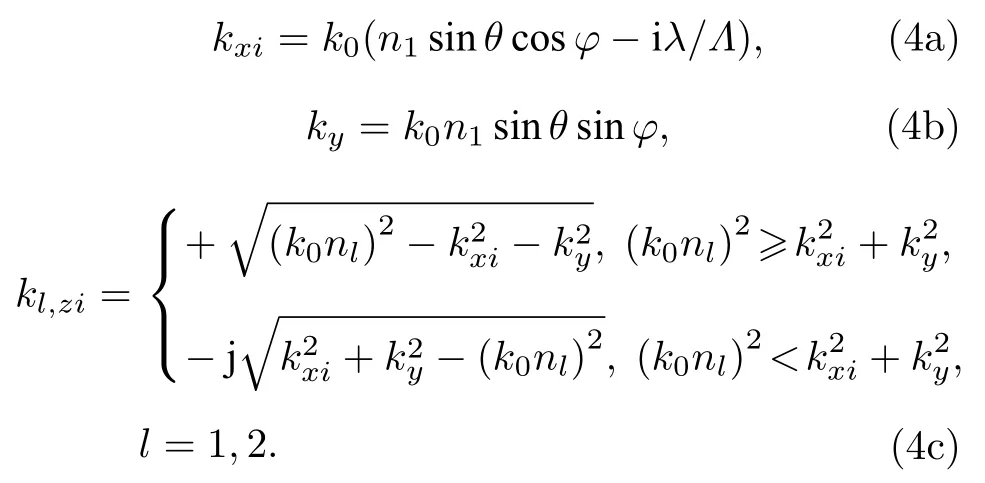
在光柵區域(0 ＜ z ＜ d)內, 電場 Eg和磁場Hg可以表示為空間諧波的Fourier級數展開式[12]：

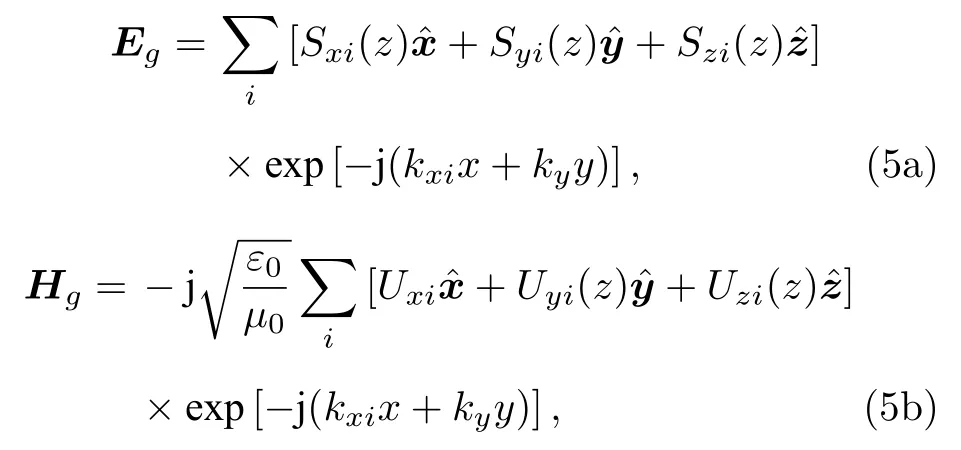
其中, Si(z) 和 Ui(z) 分別為光柵區域內電場和磁場的幅值矢量, ε0和 μ0分別為自由空間的介電常數和磁導率.

由Maxwell旋度方程, Eg與Hg有如下的耦合關系：

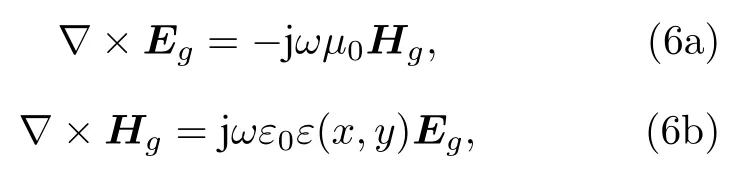
將(5)式代入(6)式, 消去Egz與Hgz, 并應用逆規則[28]后, 可得矩陣形式的耦合波方程組.當所研究的結構具有非矩形面型(如圖1所示)需要進行分層處理時, 應在光柵區域每一層中對電場Eg和磁場Hg進行展開, 并獲得相應的耦合波方程.最后在光柵區域內各層邊界及光柵區域與反射區和投射區的分界面(z = 0和z = d)上考慮連續性條件, 即可得出反射波 TE (ψ = 90°)模電場分量 Rs和 TM (ψ = 0°)模磁場分量 Rp的幅值向量.

考慮到儀器探測設備主要檢測的是光強信息,基于RCWA模型輸出的相應為反射率、橢偏參數或Mueller矩陣等光學特性參量的計算值.其中,反射率的計算公式為

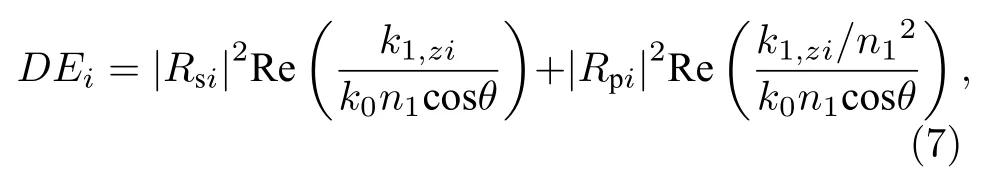
其中Rsi和Rpi分別表示第i級反射波TE模電場分量和TM模磁場分量的幅值向量.

由偏振光學可知, 待測樣品的光學特性則可以用2 × 2階Jones矩陣J或者4 × 4階Mueller矩陣M來表征.例如, 對應于待測樣品的Jones矩陣J有

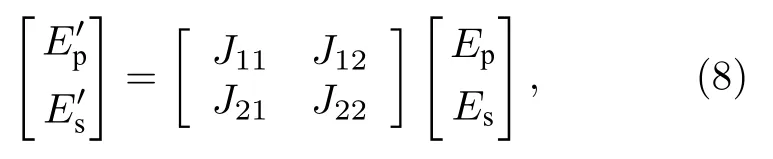
(8)式左右兩邊分別表示出射和入射至樣品表面的Jones向量, Ep和Es分別表示平行和垂直于入射面的電場分量.由Jones矩陣J可求得橢偏參數：

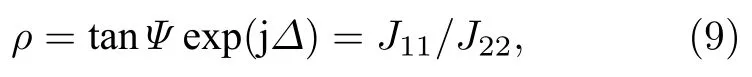
其中, Ψ為振幅比角, Δ為相位差角.當測量過程中不存在退偏效應時, 其Jones矩陣J和Mueller矩陣M之間存在如下關系：

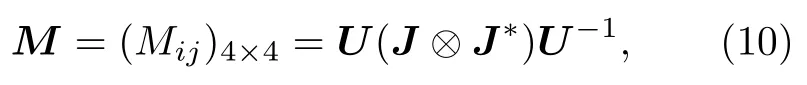
其中, ? 表示矩陣的Kronecker積; J?為Jones矩陣J的共軛矩陣; 矩陣U定義為

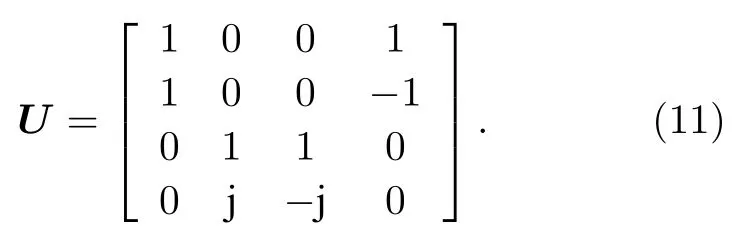
在實際測量過程中, 通常用Mueller矩陣中第1行和第1列的元素M11對其進行歸一化處理.歸一化的Mueller矩陣定義為

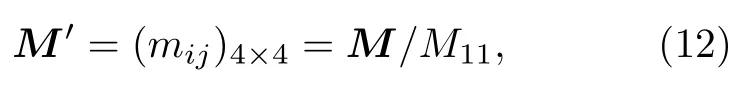
2.2 基于LM局部優化算法的待測參數逆向求解

對于光學散射測量中的逆問題, 采用非線性回歸法中的LM局部搜索算法對納米結構的待測參數進行逆向求取, 該算法結合了梯度下降法和高斯?牛頓法, 是一種采用標準數值優化的快速算法[29].不失一般性, 在參數提取過程中, 利用S維列向量表示一組需依據評價函數值的大小進行浮動變化的參數, 并記為 x = [x1, x2, ··, xS]T, 其中 x1, x2, ··,xS可以表示光柵結構的頂部線寬、線高及側壁角等待測參數; 將固定不變的參數組成的L維列向量記為 a = [a1, a2, ··, aL]T, 其中 a1, a2, ··, aL可以是測量條件、材料的光學常數, 還可以是納米結構的已知測量值的幾何特征參數, 如薄膜厚度等;數據擬合時, 采用χ2形式的評價函數來衡量測量和計算得到的橢偏參數或者Mueller矩陣元素之間的擬合誤差.

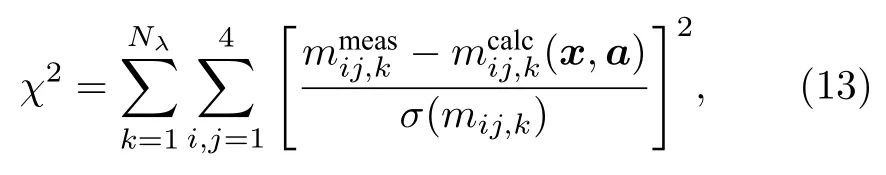
其中下標i和j表示Mueller矩陣元素索引, 這里不包括元素m11(m11≡ 1); k表示光譜點索引,Nλ為總的光譜點個數; σ (mij,k) 為測量Mueller矩陣元素 mij,k的標準差.

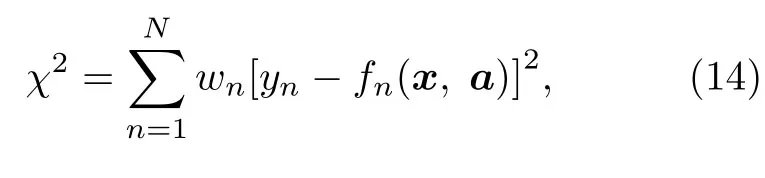
其中, wn=1/σ2(yn) 為權值因子, N =15Nλ.再將(14)式寫成矩陣形式：

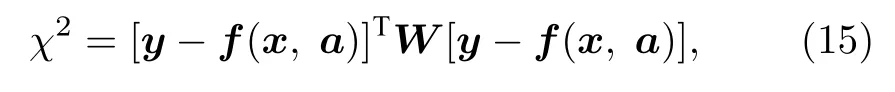
其中, y =[y1,y2, ···,yN]T,f(x,a)=[f1(x,a),f2(x,a), ···,fN(x,a)]T, W為由權值因(子wn構成的 N ×N 階對角矩陣), 即W=diag1/σ2(y1),1/σ2(y2), ···,1/σ2(yN).因此, 納米結構光學散射測量中的逆問題可以表述為

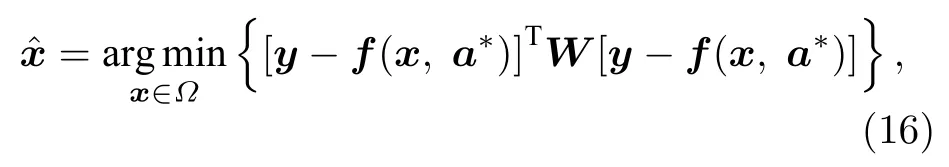
對于(16)式描述的逆問題, 本文利用LM優化算法提取待測參數的流程為：首先設置一組迭代參數初值x0, 然后利用所建正向光學特性模型計算出待測納米結構對應的理論光譜, 通過定義某種評價函數來進行理論計算光譜與測量光譜的比對,若評價函數值大于其預設的精度值, 則根據一定準則修改當前參數值, 重復上述過程, 直到評價函數值小于預設的精度值時則認為實現了理論計算光譜與測量光譜的最佳擬合, 即可得到待測參數的輸出結果.

3 實驗結果與討論

本文采用的實驗儀器是一臺由武漢某公司生產的雙旋轉補償器ME?L型Mueller矩陣橢偏儀,其實物圖與基本原理圖如圖2所示, Cr1(w1)為起偏臂的補償器, Cr2(w2)為檢偏臂的補償器, 二者在測量時將同步旋轉且旋轉角頻率之比為5∶3[30];儀器測量的光譜范圍為210—1650 nm, 入射角范圍為45°—90° (加聚焦組件入射角范圍為 55°—75°), 樣品臺可360°旋轉, 常規光斑直徑約為3 mm(加聚焦組件時光斑直徑約為200 μm), 單次數據測量時間為1—8 s, 測量參數包括反射率、橢偏參數及15個歸一化的Mueller矩陣元素等.

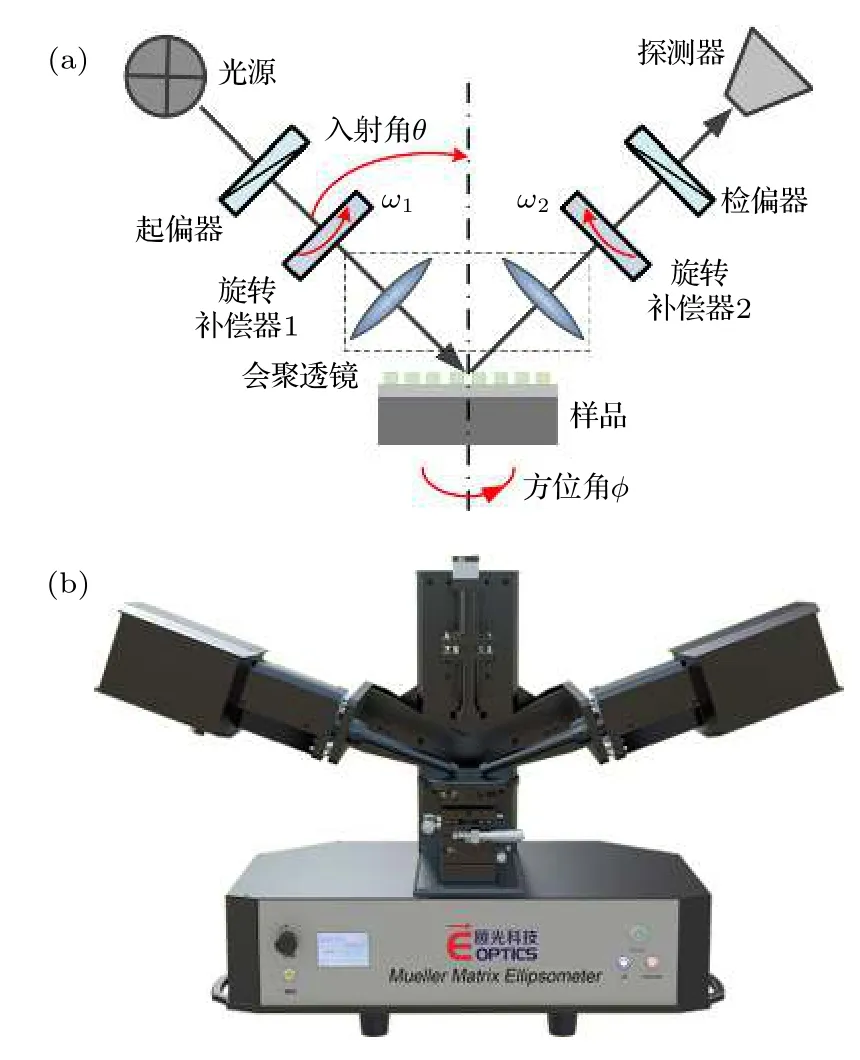
圖2 雙旋轉補償器型Mueller矩陣橢偏儀 (a)基本光路;(b)儀器Fig.2.Principle and instrument of the dual rotating?com?pensator Mueller matrix ellipsometer：(a) Principle; (b) in?strument.

實驗樣品為光柵制作前期工藝中的兩個薄膜樣品, 樣品1是基底為標準硅片(silicon, Si)的單層二氧化硅(silicon dioxide, SiO2)薄膜結構, 其SiO2薄膜厚度的名義值為100 nm, 如圖3(a)所示;樣品2為在上述SiO2薄膜結構表面旋涂了一層PMMA的光刻膠培片, 其PMMA薄膜厚度的名義值為385 nm, 如圖3(b)所示.其中, 第1個薄膜樣品的待測參數包括SiO2薄膜的厚度值d1、表面粗糙度c1及其光學常數折射率n1和消光系數k1;第2個樣品的待測參數為PMMA薄膜的厚度值d2、表面粗糙度c2及其光學常數折射率n2和消光系數k2.

為了分析橢偏儀入射光對PMMA光刻膠的影響, 首先, 利用ME?L型Mueller矩陣橢偏儀在65°入射角下分別對圖3所示的兩個薄膜樣品進行了20次重復性實驗, 各獲得20組橢偏參數測量數據, 由于儀器測量時間以及人工操作的時間消耗,單次測量過程大約耗時15 s, 因此每個樣品在入射光下的總暴露時間約為300 s.然后, 利用上述LM迭代算法分別從每組橢偏參數測量數據中提取出薄膜樣品的所有待測參數.

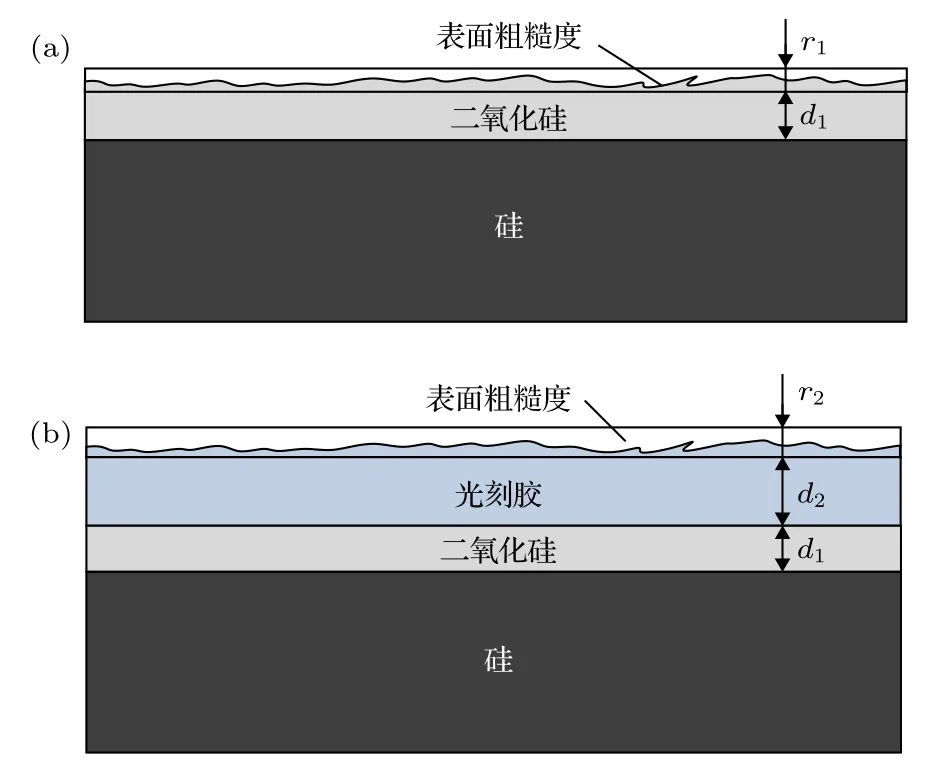
圖3 (a) SiO2薄膜樣品; (b) 在SiO2表面旋涂PMMA光刻膠后的薄膜樣品Fig.3.(a) The SiO2 sample; (b) the PMMA sample spin?ning coated on the surface of the SiO2 film.

在樣品1的參數提取過程中, 對于SiO2光學常數中的n1和k1這兩個待測參數, 我們采用Cauchy模型[31]對其進行建模, 通過一個三項式來描述材料的折射率n1, 如(17a)式所示; Urbach尾部的指數吸收則采用(17b)式進行描述.

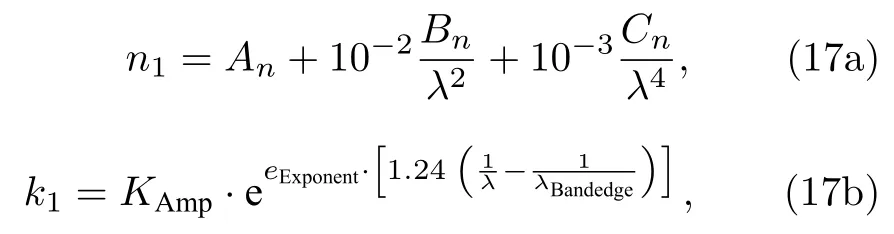
其中, An, Bn和Cn描述折射率的色散; KAmp(K振幅)和eExponent(指數)項描述消光系數色散的形狀;λBandedge一般設為定值400 nm.模型中的An, Bn,Cn, KAmp和eExponent均為待定系數.對于樣品表面的粗糙結構, 采用麥克斯韋爾?加內特等效介質模型 (maxwell?garnett effective medium approxi?mation, MGEMA)[32]將其近似為一層均勻且各項同性的薄膜進行處理.在此基礎上, 將入射條件和基底硅的光學常數等設為已知值, 利用LM迭代算法分別對20組橢偏測量數據進行待測參數逆向求取, 并采用均方根誤差(mean squared error,MSE)[33]來衡量測量與模型計算數據之間的擬合程度, 待測參數包括d1和r1, 光學常數模型參數n(∞), Eg, Ai, Bi和 Ci.圖4為 SiO2厚度 d1及其表面粗糙層厚度r1的20組擬合值; 圖5分別展示了第1, 5, 10, 15和20次所提取得到的各波長下折射率n1與消光系數k1值, 以及文獻[34]中的SiO2光學常數變化曲線.

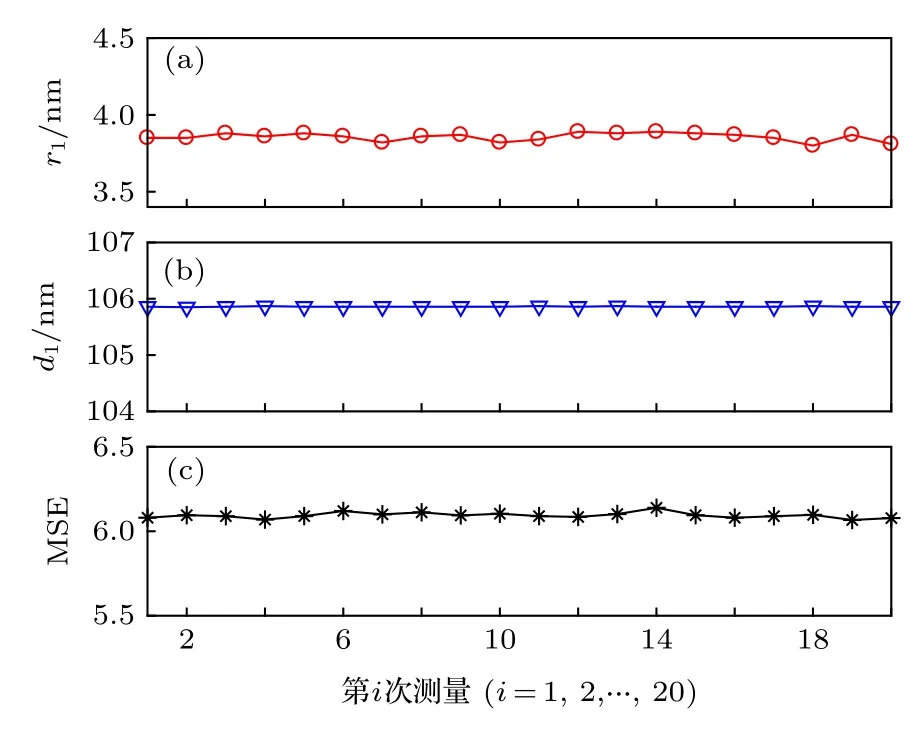
圖4 擬合得到的20組SiO2膜厚d1及其表面粗糙度等效膜厚r1 (a) r1; (b) d1; (c) MSEFig.4.Extracted results of the thicknesses of SiO2 film h1 and equivalent surface roughness r1：(a) r1; (b) d1; (c) MSE.

對樣品2的待測參數進行逆向提取時, 除了將入射條件(如入射角、入射波長等)、基底硅的光學常數等設為已知量, 還將SiO2薄膜層的厚度、光學常數及粗糙度厚度均固定為樣件一中20組提取結果的平均值; 對于PMMA光刻膠光學常數中的n2和k2這兩個待測參數, 同樣采用Cauchy模型對其進行建模, 其表面的粗糙結構也采用MGEMA模型將其等效為均勻且各項同性的一層薄膜.在此基礎上, 利用LM迭代算法分別對20組橢偏測量數據進行待測參數逆向求取, 待測參數包括d2和r2, 光學常數模型參數 n (∞) , Eg, Ai, Bi和Ci.圖6中的藍色圓圈為PMMA光刻膠厚度d2及其表面粗糙層厚度r2的20組提取值, 圖7分別展示了第1, 5, 10, 15和20次所提取得到的各波長下折射率n2與消光系數k2值.此外, 將第1次提取得到的PMMA光學常數作為已知量后, 再從后續的19組測量數據中提取出待測參數d2和r2, 其擬合值如圖6中的紅色方形所示.

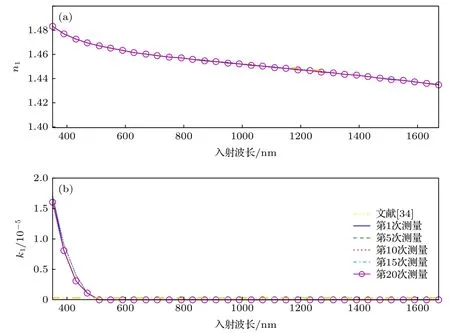
圖5 擬合得到的第1, 5, 10, 15和20組SiO2薄膜光學常數n1和k1的計算值, 以及文獻[34]給出的折射率與消光系數 (a) n1; (b) k1Fig.5.Extracted results of the optical constants n1 and k1 of SiO2 film calculated by Cauchy model and the ones from Ref.[34]：(a) n1; (b) k1.

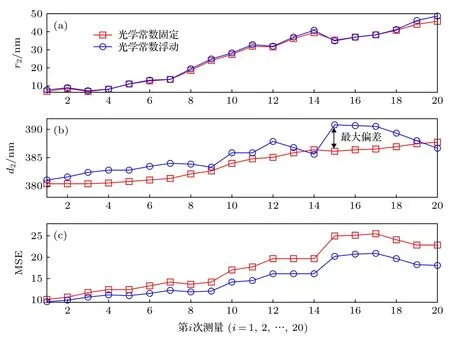
圖6 擬合得到的20組PMMA膜厚d2及其表面粗糙度等效膜厚r2 (a) r2; (b) d2; (c) MSEFig.6.Extracted results of the thicknesses of PMMA film d2 and equivalent surface roughness r2：(a) r2; (b) d2; (c) MSE.

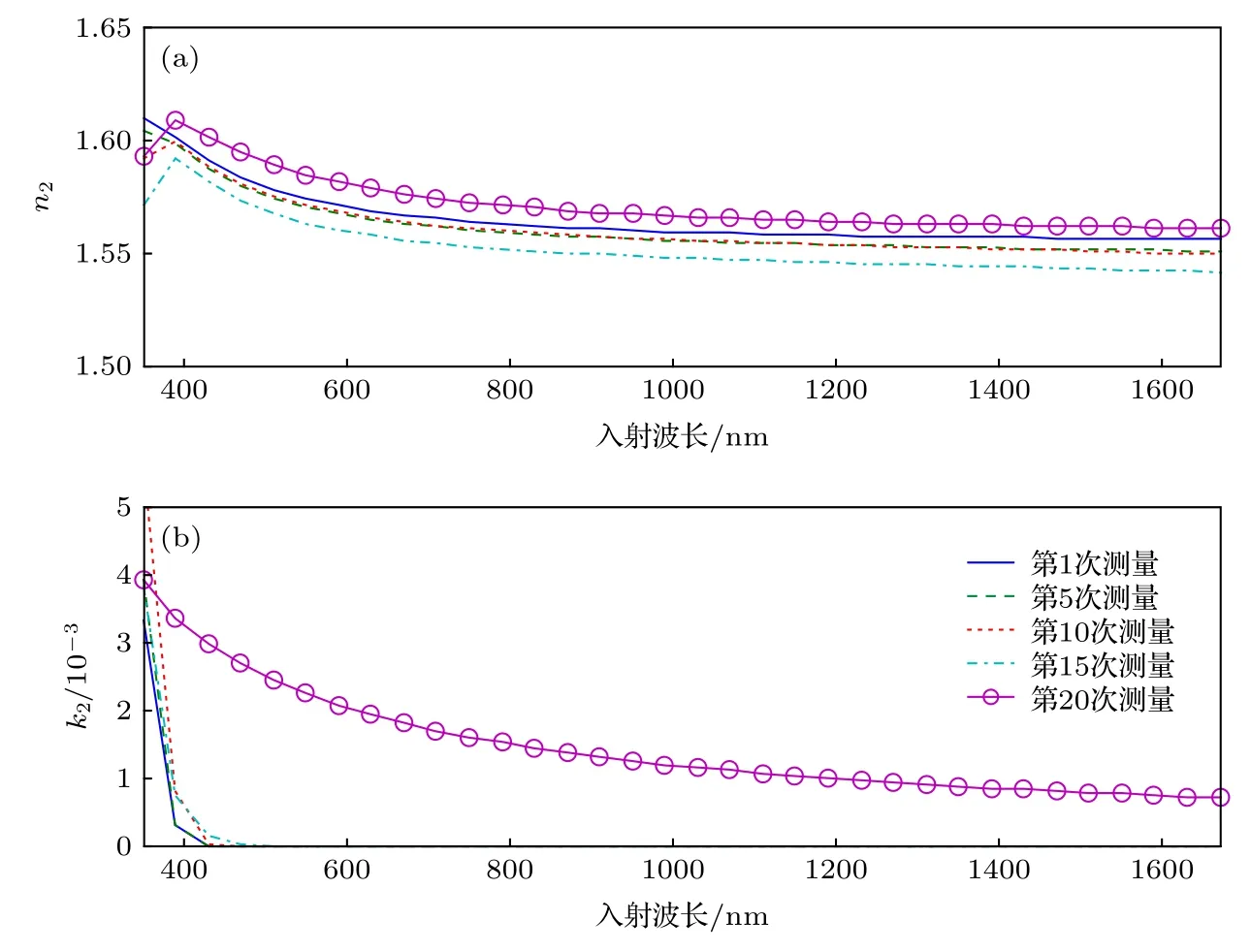
圖7 擬合得到的第1, 5, 10, 15和20組PMMA薄膜光學常數n2和k2的計算值 (a) n2; (b) k2Fig.7.Extracted results of the optical constants n2 and k2 of PMMA film calculated by Cauchy model：(a) n2; (b) k2.

從圖4和圖5可以看出, SiO2薄膜樣品折射率n1的提取值與文獻[34]中的結果幾乎保持一致, 且k值的差別為10—5量級(由于k很小, 可忽略不計, 故文獻[34]中設定k = 0); SiO2薄膜樣品在20次重復性測量數據中擬合得到的折射率n1、消光系數k2以及薄膜厚度d1幾乎一致, 其表面粗糙度參數r1的變化幅度也不大, 均位于3.82 nm左右.由圖6和圖7可得, 隨著入射光照射時間的增加, 重復20次提取得到的PMMA光刻膠折射率n2、消光系數k2、膜厚d2以及表面粗糙度參數r2均存在明顯差異, 尤其是第20次得到的k2變化更為劇烈, 可能的原因為PMMA光刻膠到達一定曝光時間后, 其光學特性進入非線性變化區域[35].其中, 光刻膠厚度d2大約在380—392 nm的范圍內上下波動, 而表面粗糙度r2的變化幅度較大且呈現上升趨勢, 其第1次測量的擬合值為7.93 nm,到第20次測量時為48.43 nm, 變化幅度高達40.5 nm.對比圖6(a)中光刻膠光學常數浮動(藍色圓圈)與固定(紅色方形)的提取結果可得, 光刻膠光學常數的變化對表面粗糙度r2的測量結果影響較小, 而光刻膠厚度d2(紅色方形)明顯不同且小于在光學常數浮動時的擬合值(藍色圓圈), 二者之間的最大差值達到3.5 nm.此外, 在20次橢偏光譜數據的擬合中, 光學常數固定時得到MSE值均大于其浮動的結果, 即在光刻膠光學常數浮動時, 達到最佳擬合所對應的模型計算橢偏光譜與儀器測量光譜之間的匹配度更高.上述實驗結果表明, SiO2材料不受入射光照射的影響, 而PMMA光刻膠薄膜樣品, 尤其是其折射率n2和消光系數k2受到顯著影響, 若在待測PMMA薄膜的光學散射測量中將其作為固定量, 則會較大地降低樣品薄膜厚度的測量精確度.

4 仿真結果與討論

在光柵結構三維形貌的光學散射測量中, 為了極大地降低待測參數之間的耦合作用, 通常需要事先測量結構刻蝕前的薄膜培片以確定光柵材料的光學常數, 從而在逆向提取待測形貌參數時將其設為固定值.為分析PMMA光學常數的變化對光柵結構測量結果的影響, 以圖8所示的PMMA光刻膠光柵為仿真對象, 結合上述PMMA薄膜樣品的實驗結果開展光柵結構待測形貌參數的逆向提取研究.圖8所示的PMMA光刻膠光柵是在薄膜樣品2的基礎上刻蝕后得到, 其幾何形貌參數包括周期P、頂部線寬w1、線高h以及底部線寬w2.

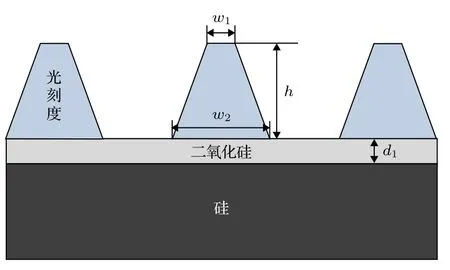
圖8 PMMA光刻膠仿真光柵的結構示意圖Fig.8.Geometry of the simulated PMMA grating sample.

具體的仿真過程為：假設光柵結構的真實尺寸為P = 800 nm, w1= 350 nm, h = 387.42 nm, w2=365 nm, PMMA的光學常數n2和k2均取值為圖7中的第20次擬合結果, 硅基底和SiO2薄膜的光學常數、厚度等參數信息均與樣品2的取值相同;在入射角θ = 65°、方位角φ = 0°和入射波段為370—870 nm (步長為10 nm)的入射條件下, 利用所建立的基于RCWA的正向光學特性模型計算得到該PMMA光刻膠光柵的一組Mueller矩陣元素, 并將其看作“測量”光譜數據; 在其他參數保持不變的前提下, 將PMMA光學常數n2和k2的取值替換為圖6中的第1次擬合結果后, 以頂部線寬w1、線高h和底部線寬w2為浮動的待測參數,利用LM迭代尋優算法不斷調用正向光學特性模型, 并將計算光譜與“測量”光譜進行匹配, 當二者實現最佳匹配后所對應的3個待測形貌參數的擬合值如表1所列, 圖9所示為模型計算與“測量”光譜之間的擬合程度.

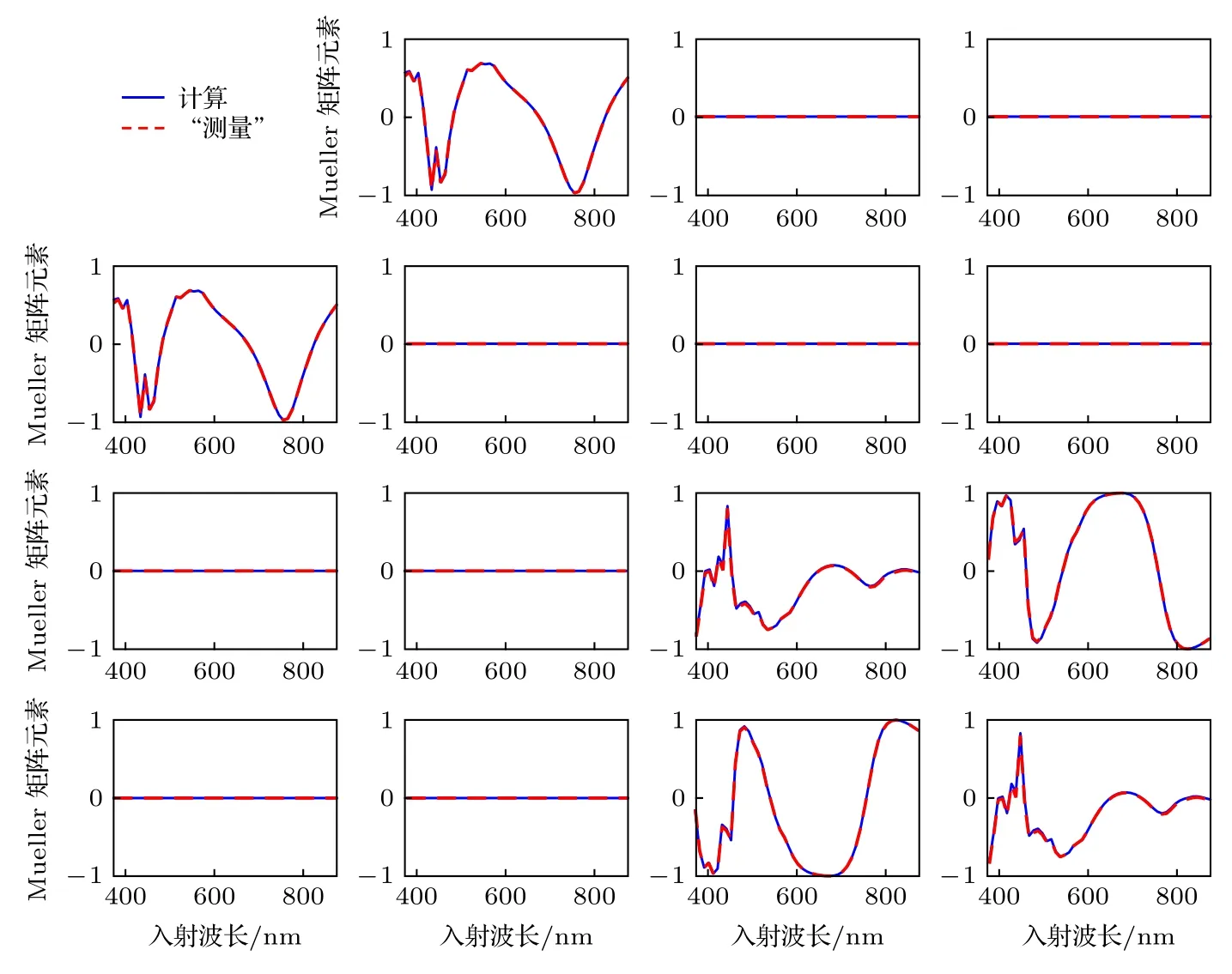
圖9 在入射角θ = 65°、方位角φ = 0°的入射條件下, PMMA光刻膠仿真光柵的模型計算Mueller矩陣光譜與“測量”光譜之間的擬合曲線Fig.9.Fitting results of the calculated and the “ellipsometer?measured” Mueller matrix elements at the incidence and azimuthal angles fixed at θ = 65° and φ = 0°.

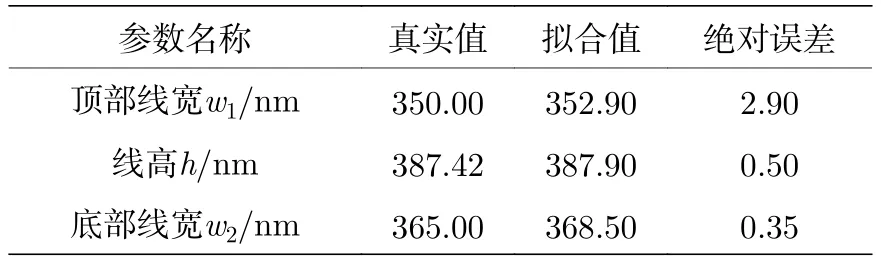
表1 對比PMMA仿真光柵3個待測形貌參數的擬合值與真實值Table 1.Comparison of these three true dimen?sions and the extracted results of the simulated PMMA grating.

由表1可得, 在對“測量”光譜進行待測參數提取時, 改變PMMA光刻膠光學常數n2和k2的取值后, 3個結構參數頂部線寬w1、線高h和底部線寬w2的提取結果在一定程度上偏離于真實值.其中, 引起待測形貌參數頂部線寬w1的測量誤差為最大, 達到了2.90 nm.本文第3節中光刻膠薄膜的測量實驗研究證明了光刻膠的光學常數受到橢偏儀入射光的照射影響后會發生明顯的變化, 這里光刻膠光柵的仿真結果表明了光刻膠光學常數的變化將較大地降低光柵結構幾何形貌參數的測量準確度.因此, 針對半導體制造工業中光刻膠納米結構的光學散射測量而言, 其光學常數會隨著入射光照射時間增加而發生變化這個特性將不能再被忽略, 這對于實現光刻膠納米結構三維形貌參數的高精確度測量具有較為重大的指導意義.

5 結 論

利用Mueller矩陣橢偏儀分別對SiO2薄膜和PMMA光刻膠薄膜進行了包括光學常數、厚度和表面粗糙度的待測參數提取實驗研究, 首次發現了PMMA光刻膠的光學常數(折射率和消光系數)受到入射光的照射影響會發生相應的改變.結合實驗得到的PMMA光學常數提取結果, 針對仿真的PMMA光刻膠光柵進行了幾何形貌參數頂部線寬、線高和底部線寬的逆向提取研究, 結果表明光刻膠光學常數隨入射光照射發生的變化對光柵形貌參數提取結果的影響較大, “材料光學常數不隨入射光的照射而發生變化”這一假設條件將不再適用.在后續的研究工作中, 我們將深入研究光刻膠材料折射率和消光系數受入射光照射的影響規律并建立相應的變化模型, 從而可進一步提高光刻膠納米結構三維形貌參數的測量準確度.