懸臂式電磁發射導軌及壁板在發射狀態下的強度分析

何威，魏彥京

(1.燕山大學 建筑工程與力學學院，河北 秦皇島 066004；2.中國科學院大學，北京 100049)

0 引言

電磁發射器的研究意義極其重大，它將對一個國家的能源、運輸、防御和空間規劃產生重大影響[1]，因此多年來各國政府對此問題的研究都極為關注。自20世紀80年代以來，電磁發射裝置技術的研究取得了多方面進展，應用領域日益廣闊。尤其在軍事工業方面，經過多年的努力，用于電磁軌道炮的科學技術取得了相當大的進展，并已經在軍事應用中進行實踐探索，充分體現在電磁軌道炮作戰系統的研究。而在達到武器化和實用化前，仍需解決一些工程技術和制造工藝方面的難題[2-4]。其中軌道裝置的強度、剛度設計計算是保證發射精度的重要因素。目前，國內外學者對電磁軌道發射裝置的力場做了大量的理論分析和計算工作[5]。Tzeng將電磁發射裝置軌道簡化為彈性基礎梁，求解了磁場壓力下軌道炮內膛的應變場和應力場[6-8]。Johnson等[9]同樣將電磁軌道發射裝置的軌道簡化為彈性地基梁，運用材料力學的方法進行計算，初步分析了電磁軌道在電磁壓力作用下應力波的傳遞特性。Jin等[10]將電磁炮軌道簡化為Bernoulli-Euler梁，研究了電磁炮動態響應，并用數學計算軟件MATLAB進行了數值模擬，Che等[11]同樣基于Bernoulli-Euler梁理論將電磁炮軌道簡化為單層梁，討論了不同約束及預應力對軌道振動及剛度的影響。Cao等[12]運用Winkler梁模型分析了軌道的變形，而Lee等[13]運用Timoshenko地基梁分析了軌道的動態響應。田振國等[14]將復合電磁炮軌道簡化為彈性基礎梁，運用二維Fourier變換的方法求得了軌道在動荷載下的動態位移。

上述關于方型電磁軌道發射裝置的研究，主要是建立在單層梁的基礎上，目前已有雙層彈性基礎梁動態研究成果，都停留在將電磁炮軌道簡化成簡支型雙層彈性基礎梁[15-16]，而其實際結構更接近懸臂式雙層彈性基礎梁。因此，為完善電磁發射裝置理論，找到更加接近實際工況的理論模型是非常必要的。

本文將方型電磁軌道炮的炮管(見圖1)簡化為懸臂梁，其內部的導軌和壁板簡化為懸臂梁內部的上下彈性基礎梁，求解了上、下梁在電磁力與電樞力共同載荷作用下的解析和數值解。

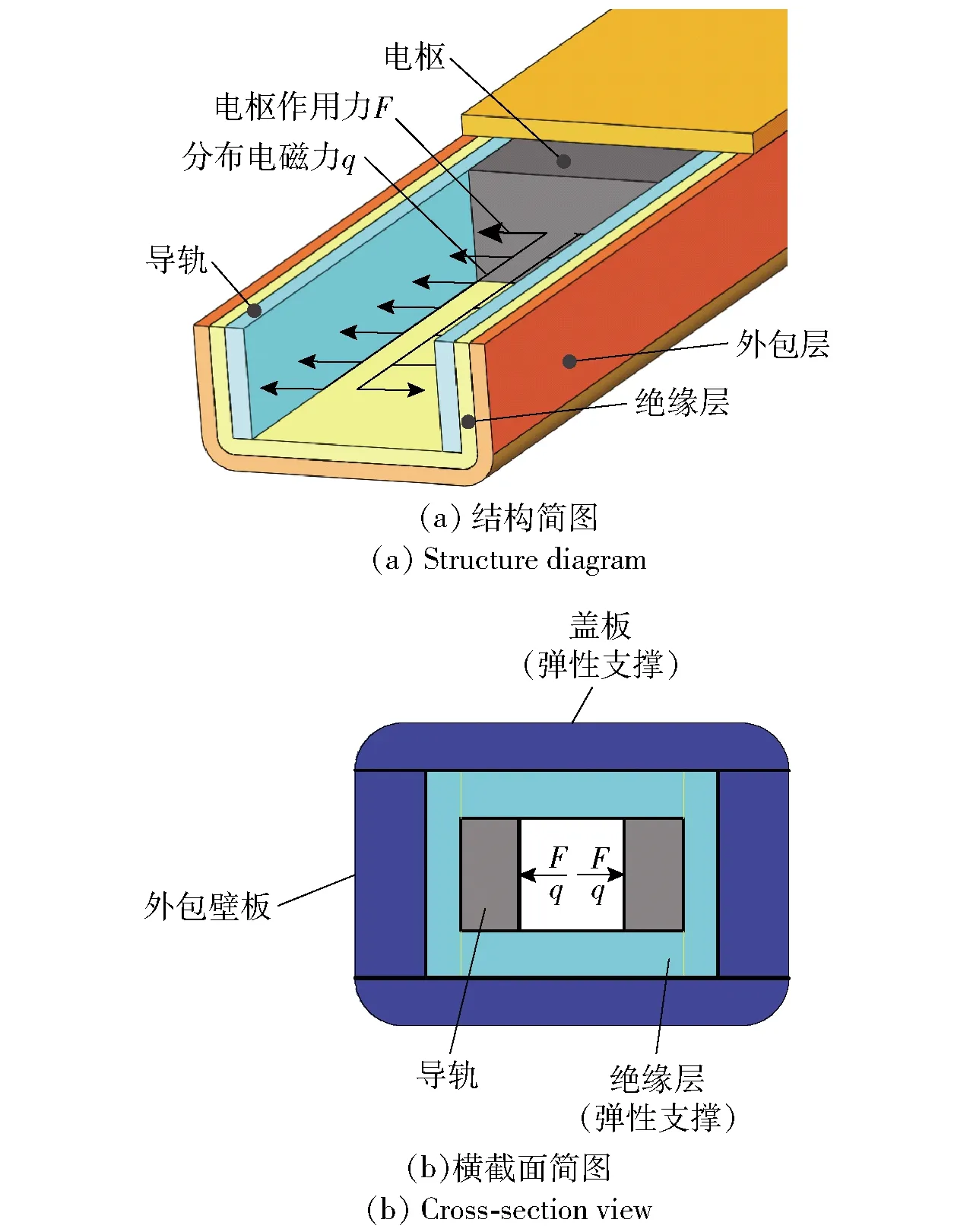
圖1 方形電磁軌道發射裝置簡圖

1 雙層彈性懸臂梁動力學微分方程式的建立

1.1 雙層彈性懸臂梁的力學模型及動力學微分方程的建立

發射導軌和外包層壁板簡化成Winkler彈性地基上的雙層梁體系，雙層彈性懸臂梁模型如圖2所示。圖2中：Eu、Ed分別為上、下梁的彈性模量；Iu、Id分別為上、下梁的慣性矩；EuIu、EdId分別為上、下梁的抗彎剛度；cu、cd分別為上、下梁的彈性常數；l為梁長，le為電樞位置；v為電樞速度。

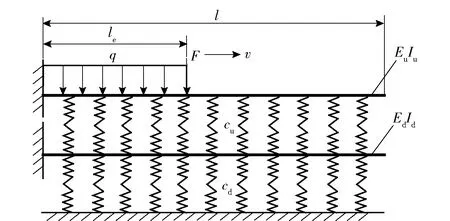
圖2 雙層懸臂梁力學模型圖

上、下梁的動力學平衡方程為

(1)

式中：mu、md分別為上、下梁單位長度的質量，mu=ρuSu,md=ρdSd，ρu、ρd、Su、Sd分別為上、下梁的質量密度與截面面積；wu(x)、wd(x)分別為上、下梁的撓度；t為時間；f(x,t)為集中荷載F(即電樞作用力)和均布荷載q(即作用在軌道上的電磁力)之和，x為集中荷載F的水平位移。

1.2 雙層彈性懸臂梁的動力學方程及其通解表達式的建立

根據上、下梁的相互作用關系，在無載荷作用的情況下，上、下梁的動力學方程分別為

(2)

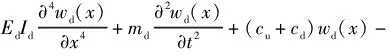
cuwu(x)=0.

(3)

由(2)式可得

(4)

(4)式代入(3)式，化簡后有

(5)

根據梁的振動形式，設wu(x)、wd(x)的通解形式分別為

(6)

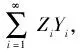
(7)

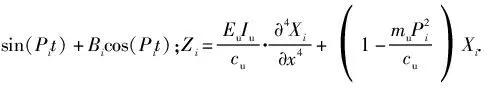
(6)式代入(5)式，可得

(8)

解偏微分方程(8)式，可得

Xi=C1icos(Mix)+C2isin(Mix)+C3icosh(Mix)+

C4isinh(Mix)+C5icos(Nix)+C6isin(Nix)+

C7icosh(Nix)+C8isinh(Nix)，

(9)

(9)式代入(7)式，得到wd(x)表達式中的Zi為

Zi=C1iJicos(Mix)+C2iJisin(Mix)+

C3iJicosh(Mix)+C4iJisinh(Mix)+

C5iKicos(Nix)+C6iKisin(Nix)+

C7iKicosh(Nix)+C8iKisinh(Nix)，

(10)

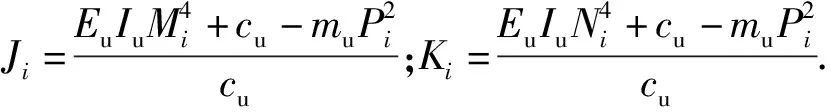
由此可得上、下梁的彎矩分別為

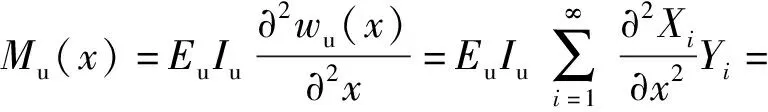
(11)

(12)

上、下梁的轉角分別為

C3iMisinh(Mix)+C4iMicosh(Mix)-C5iNisin(Nix)+

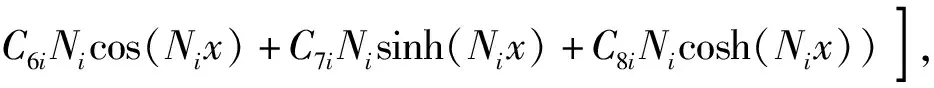
(13)

C3iJiMisinh(Mix)+C4iJiMicosh(Mix)-

C5iKiNisin(Nix)+C6iKiNicos(Nix)+

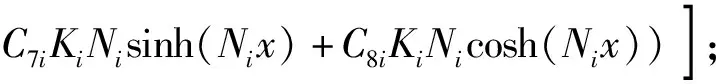
(14)

上、下梁的剪切力

(15)

(16)

系數C1i～C8i由上、下梁的邊界條件確定，對照所建立的電磁軌道系統雙層梁分析模型，則在上、下梁一端固定約束、一端自由的條件下，所得到的雙層梁左、右兩端的邊界條件為

(17)

(6)式、(7)式、(13)式、(14)式代入(17)式邊界條件，可解得

(18)

由此可得到關于上、下梁的模態函數為

Xi=-cos(Mix)+cosh(Mix)-

cos(Nix)+cosh(Nix)-

(19)

Zi=-Jicos(Mix)+Jicosh(Mix)-

Kicos(Nix)+Kicosh(Nix)-

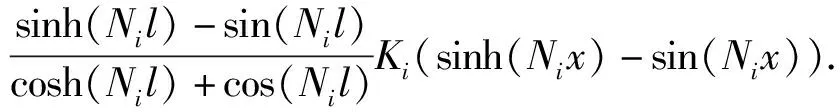
(20)

因此wu(x)和wd(x)可以分別表示為

wu(x)=

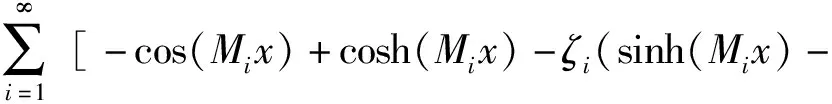
sin(Mix))-cos(Nix)+cosh(Nix)-ξi(sinh(Nix)-

sin(Nix))](Aisin(Pit)+Bisin(Pit))，

(21)

ζiJi(sinh(Mix)-sin(Mix))-

Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-

sin(Nix))](Aisin(Pit)+Bisin(Pit))，

(22)

1.3 發射狀態下載荷的表達形式

根據雙層梁模態函數的正交性，可將多自由度系統模態疊加法的思想應用于連續系統，即將彈性體的振動表示為各階模態的線性組合，用于計算系統在激勵作用下的振動規律，則根據上、下梁的受載狀態，其載荷函數為

(23)

式中：δ(·)為Dirac函數；H(·)為Heaviside函數。

由載荷函數(23)式可知，在電樞運動下，雙層梁所受載荷可分為兩部分，即集中載荷F作用和分布載荷q作用的線性疊加，因此可以將雙層梁在載荷下的動力響應表示為這兩種載荷下動力響應之和，則雙層梁受集中載荷F作用下的載荷函數為

pF(x,t)=-Fδ(x-vt)，

(24)

雙層梁受均布載荷q作用下的載荷函數為

pq(x,t)=-qH(vt-x).

(25)

2 集中載荷與均布荷載作用下懸臂式雙層梁的動態響應

2.1 集中載荷作用下的上梁動態撓曲線方程

根據(1)式在集中載荷F作用下上梁的動力平衡方程為

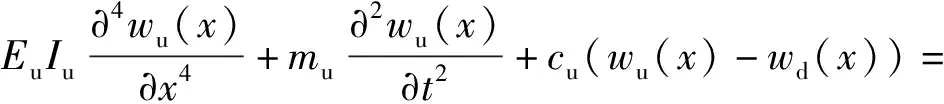
pF(x,t).

(26)

(1)式中載荷函數f(x,t)=pF(x,t)=-Fδ(x-vt)，根據上梁受載下動力響應函數的推導，將pF(x,t)代入(21)式，則有

wuF(x,t)=

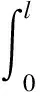
cos(Nix)+cosh(Nix)-ξi(sinh(Nix)-sin(Nix))]·

(27)

根據Dirac函數的性質，將pF(x,t)=-Fδ(x-vt)代入(27)式并積分，可得上梁在集中載荷F作用下的動態響應為

wuF(x,t)=

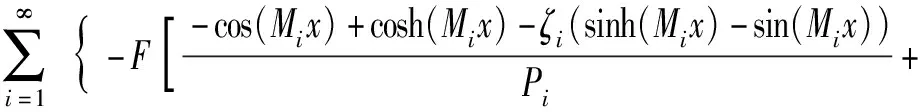
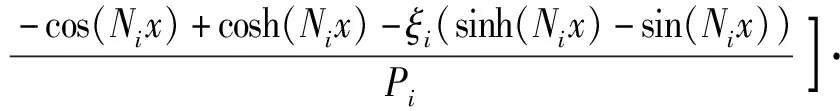
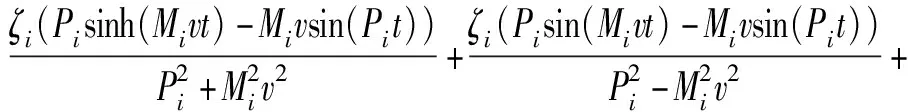
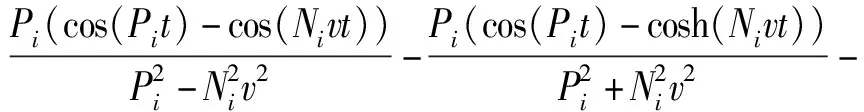
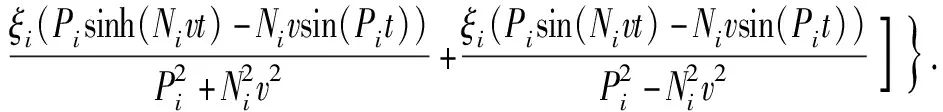
(28)

2.2 集中載荷作用下的下梁動態撓曲線方程

在集中載荷下上梁的振動響應函數wuF(x,t)確定的條件下，根據(22)式，在受集中力條件下下梁的動力響應為

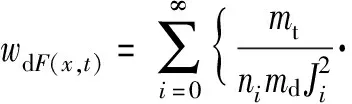
[-Jicos(Mix)+Jicosh(Mix)-ζiJi(sinh(Mix)-sin(Mix))-

Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

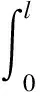
Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

(29)

2.3 集中載荷作用下的上梁彎矩及應力的動態響應

在已知上梁在集中載荷下動態撓曲線方程的情況下，根據上梁彎矩MuF(x,t)、σuF(x,t)的數值表達式，設hu為上梁截面高度，可由(28)式直接得到

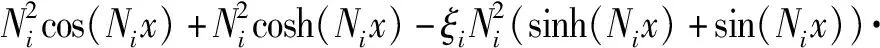
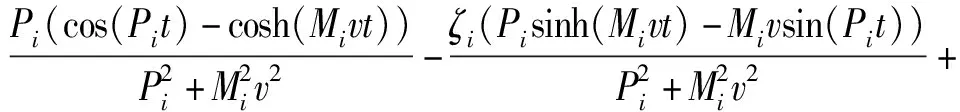
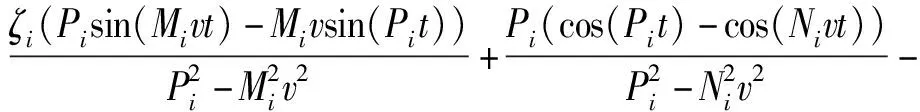
(30)

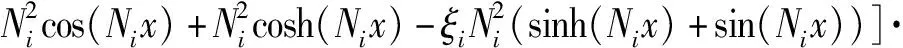
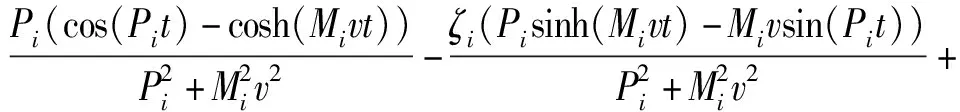
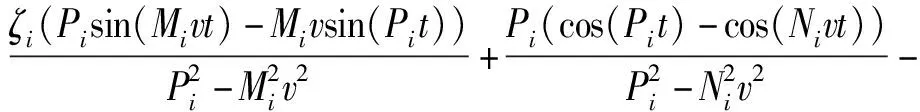
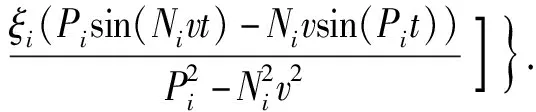
(31)

2.4 集中載荷作用下的下梁彎矩及應力的動態響應

與上梁相類似，已知下梁在集中載荷下動態撓曲線方程的情況下，根據下梁彎矩MdF(x,t)、σdF(x,t)的數值表達式，設hd為下梁截面高度，可由(29)式直接得到

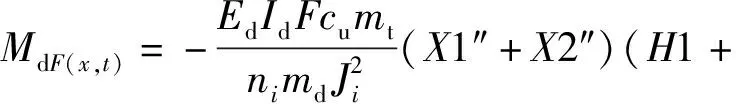
H2)(T1+T2)，

(32)

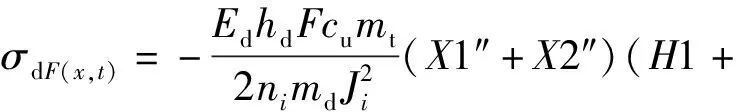
H2)(T1+T2)，

(33)

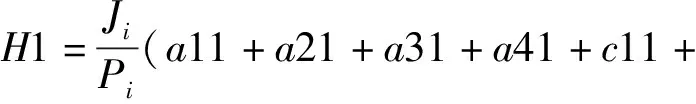
c21+c31+c41)，

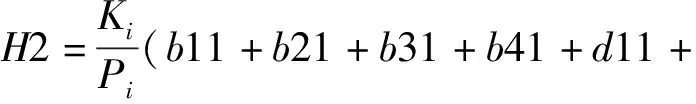
d21+d31+d41)，

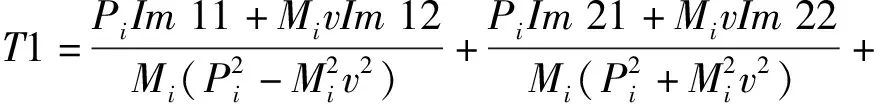
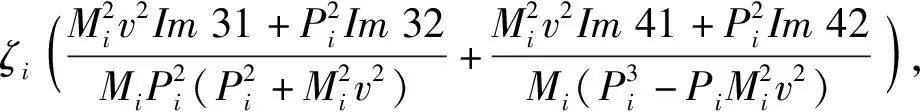
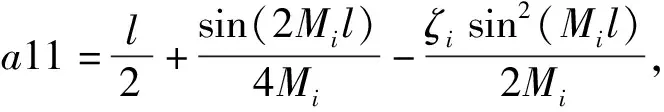
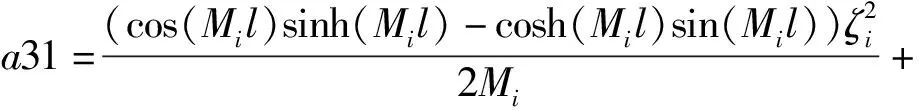
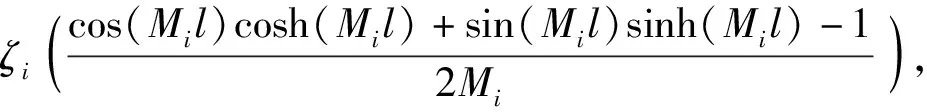
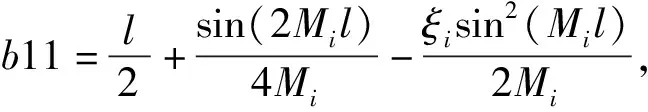
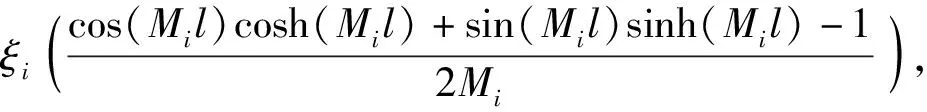
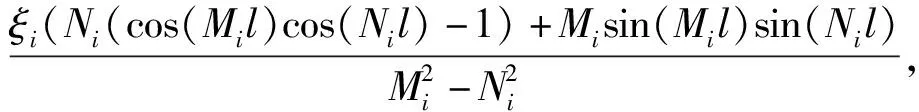
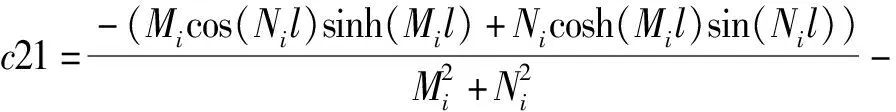
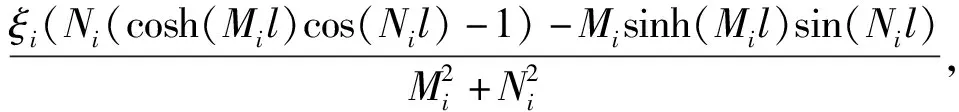
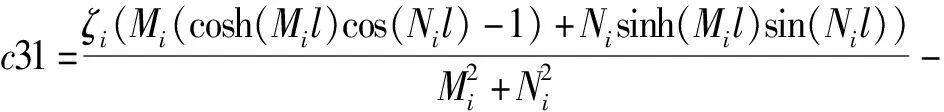
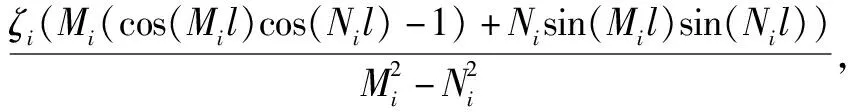
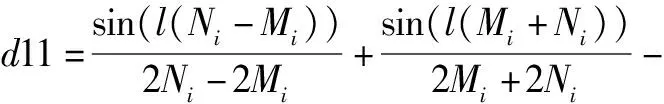
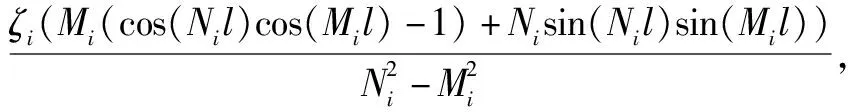
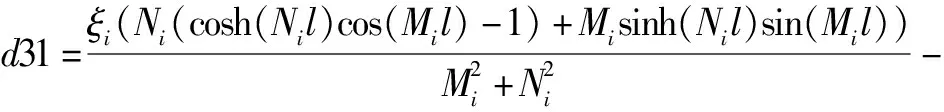
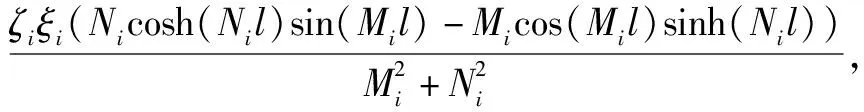
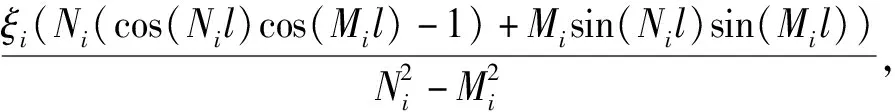
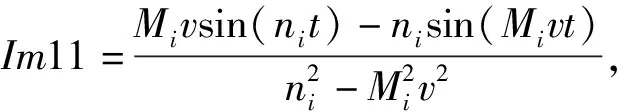
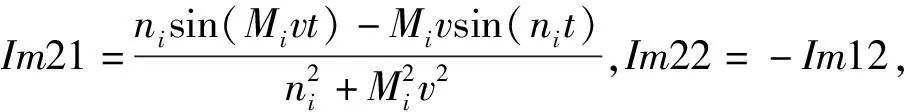
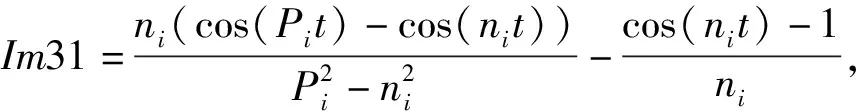
Im41=-Im31，

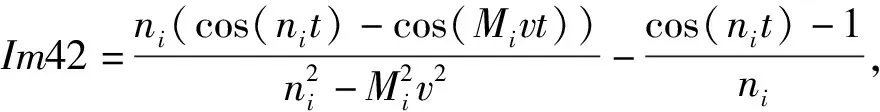
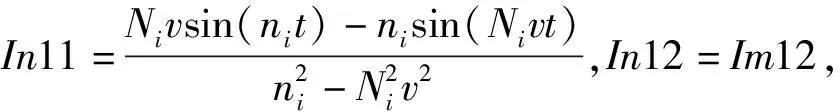
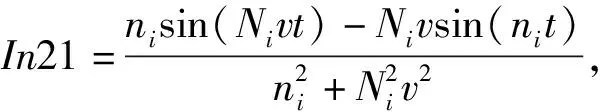
In22=-Im12，In31=Im31，

In32=Im32，In41=-Im31，

3 均布載荷作用下的上、下梁動態撓曲線方程

3.1 均布載荷作用下的上梁動態撓曲線方程

根據(1)式在均布載荷q作用下上梁的動力平衡方程為

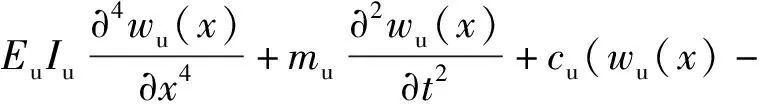
wd(x))=pq(x,t)，

(34)

即(1)式中均布函數f(x,t)=pq(x,t)=-qH(vt-x)，pq(x,t)代入(34)式，則有

wuq(x,t)=

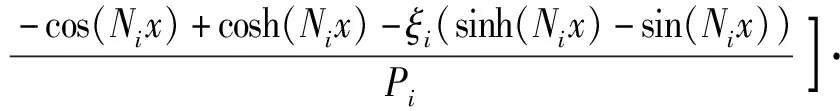
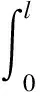
cos(Nix)+cosh(Nix)-ξi(sinh(Nix)-sin(Nix))]·

(35)

根據Heaviside函數的性質，將pq(x,t)=-qH(vt-x)代入(35)式并積分，可得上梁在均布載荷q作用下的動力響應為

(36)

3.2 均布載荷作用下的下梁動態撓曲線方程

均布載荷下的上梁振動響應函數wuq(x,t)確定的條件下，根據對受載條件下的下梁動力響應函數的推導，在受均布載荷條件下，下梁的動力響應為

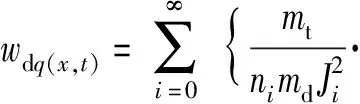
[-Jicos(Mix)+Jicosh(Mix)-ζiJi(sinhMix-sin(Mix))-

Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

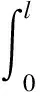
Kicos(Nix)+Kicosh(Nix)-ξiKi(sinh(Nix)-sin(Nix))]·

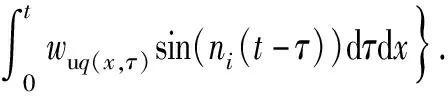
(37)

將推導的上梁在均布載荷下的振動響應函數(36)式代入(37)式并化簡，可得到下梁在均布載荷q下的動力響應為

(38)

4 均布載荷作用下的上、下梁彎矩及應力的動態響應

4.1 均布荷載作用下的上梁彎矩及應力的動態響應

在已知上梁在均布載荷下動態撓曲線方程的情況下，根據上梁彎矩Muq(x,t)、σuq(x,t)的數值表達式，可由(36)式直接得到

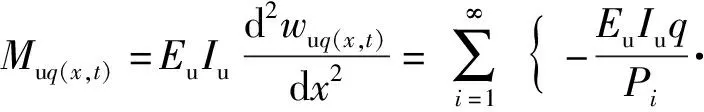
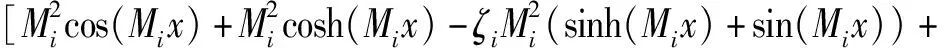
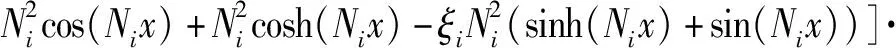
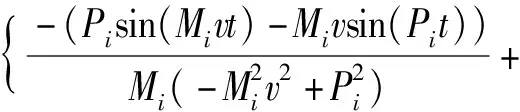
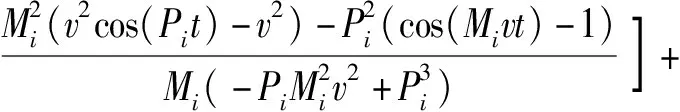
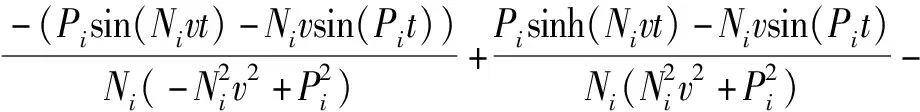
(39)

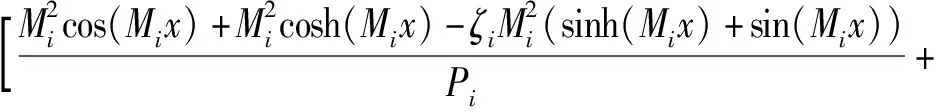
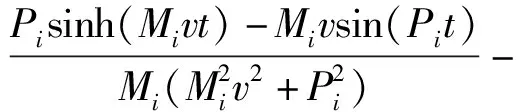
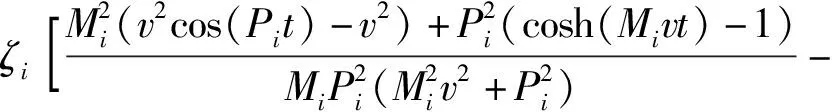
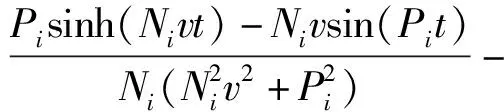
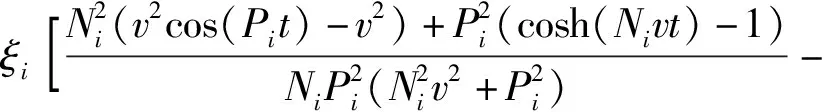
(40)

4.2 均布荷載作用下的下梁彎矩及應力的動態響應

在已知下梁在均布載荷下動態撓曲線方程的情況下，根據下梁彎矩Mdq(x,t)、σdq(x,t)的數值表達式，可由(38)式直接得到

H2)(T1+T2)，

(41)

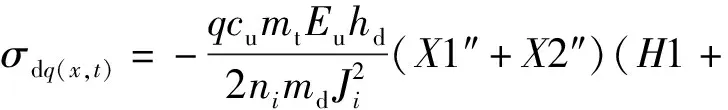
H2)(T1+T2).

(42)

4.3 綜合載荷作用下的懸臂式雙層梁的彎矩及應力響應

與雙層梁的撓曲線方程相類似，對于雙層梁的彎矩及應力響應，其也同樣具有可加性，則在綜合載荷下的上、下梁彎矩及應力的動態響應分別為

Mu(x,t)=MuF(x,t)+Muq(x,t)，

(43)

Md(x,t)=MdF(x,t)+Mdq(x,t)，

(44)

σu(x,t)=σuF(x,t)+σuq(x,t)，

(45)

σd(x,t)=σdF(x,t)+σdq(x,t)，

(46)

式中：MuF(x,t)、MdF(x,t)分別為在集中載荷下的上、下梁彎矩響應；Muq(x,t)、Mdq(x,t)分別為在均布載荷下的上、下梁彎矩響應；σuF(x,t)、σdF(x,t)為在集中載荷下的上、下梁應力響應；σuq(x,t)、σdq(x,t)為在均布載荷下的上、下梁應力響應。

5 綜合載荷作用下的懸臂式雙層梁動態響應算例分析

5.1 參數的確定

電磁發射導軌的雙層梁在綜合載荷下的動力學模型如圖2所示，截面尺寸如圖3所示。其中梁的長度l=3 000 mm，上梁的截面尺寸Hu=45 mm，hu=15 mm，下梁的截面尺寸Hd=75 mm，hd=30 mm.上梁材料為銅，其彈性模量Eu=110 GPa，密度為8 290 kg/m3；下梁材料為尼龍，其彈性模量Ed=28.3 GPa，密度為980 kg/m3;上梁和下梁之間的彈性常數cu=3 MPa，下梁和下層壁板之間的彈性常數cd=6 MPa；上梁承受的均布荷載q=300 N/m，集中荷載F=10 000 N；電樞速度為v=1 000 m/s.

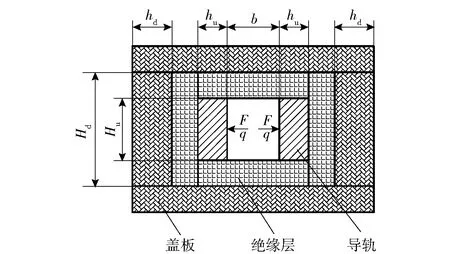
圖3 電磁軌道發射裝置橫斷面尺寸圖

5.2 計算結果與分析

圖4、圖5給出了在le=0.5 m綜合載荷作用情況下，上梁的彎矩以及應力解析解與有限元分析軟件ANSYS數值分析結果的對比。在圖4中，彎矩數值解最大值573.6 N·m，解析解最大值601.1 N·m，相對誤差為4.8%.在圖5中，應力數值解最大值339.6 MPa，解析解最大值356.2 MPa，相對誤差為4.9%.圖6、圖7給出了全程上梁彎矩以及應力隨時間和位置的變化。

圖4 上梁彎矩分布解析解與數值解的對比

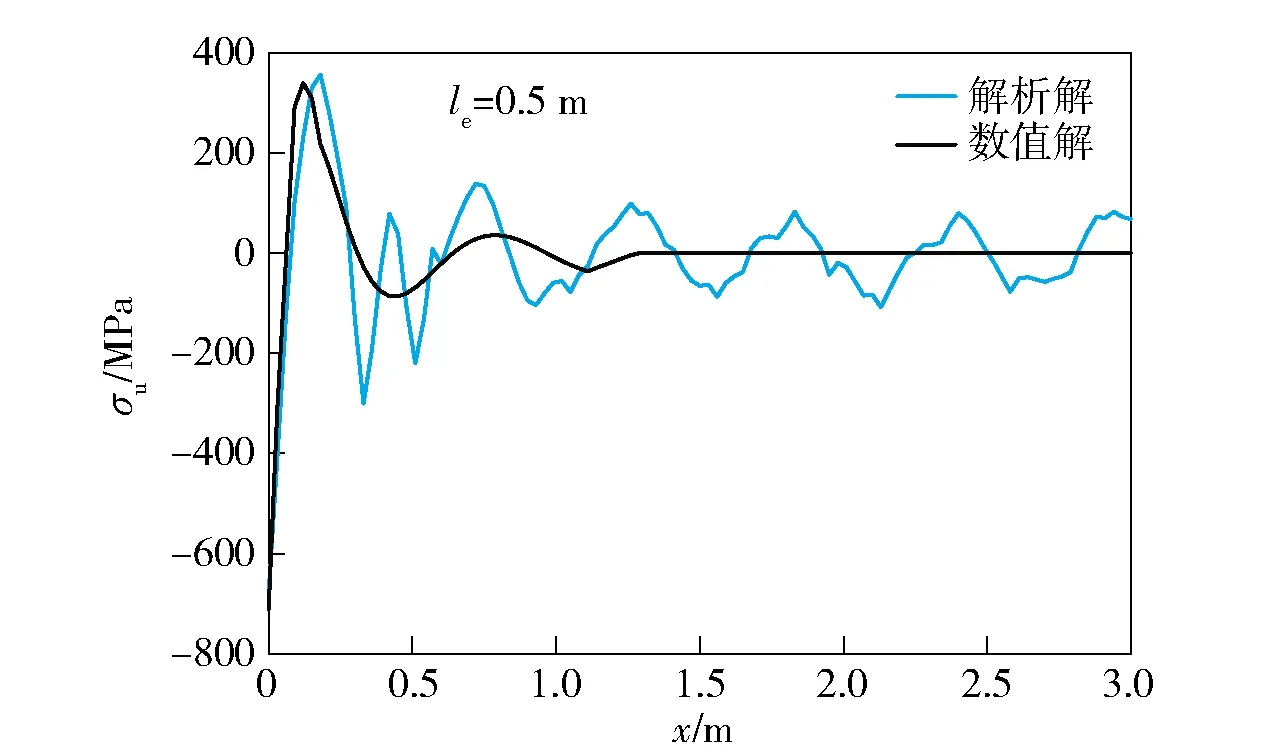
圖5 上梁應力分布解析解與數值解的對比

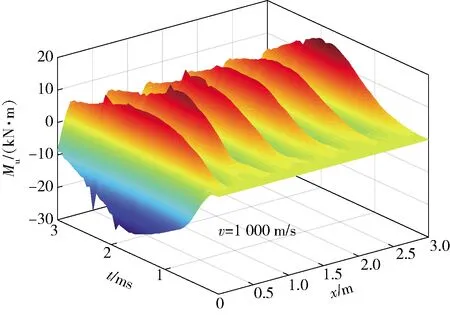
圖6 上梁彎矩隨時間和位置的變化曲面

圖7 上梁應力隨時間和位置的變化曲面

圖8 下梁彎矩分布解析解與數值解的對比

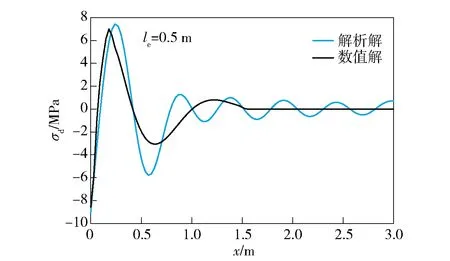
圖9 下梁應力分布解析解與數值解的對比

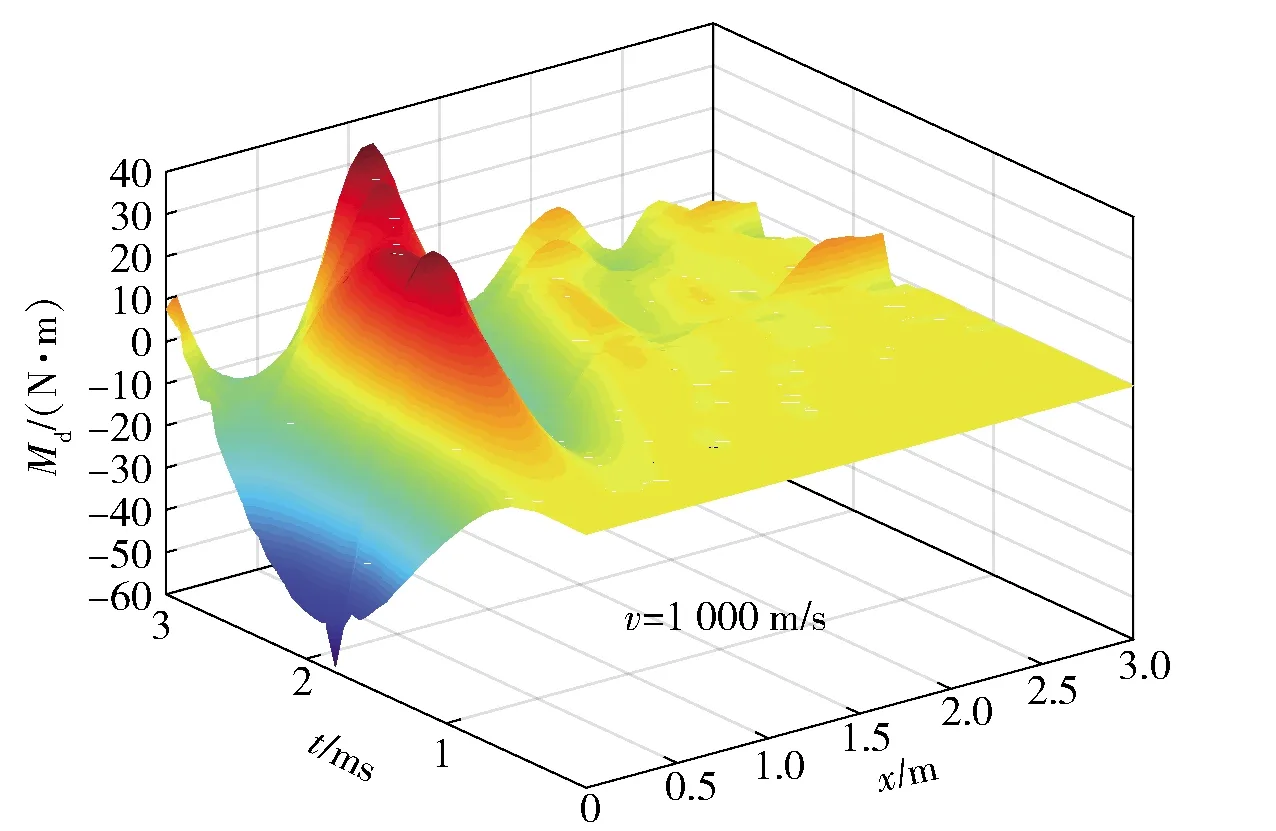
圖10 下梁彎矩隨時間和位置的變化曲面

圖8、圖9給出了在le=0.5 m綜合載荷作用情況下，下梁的彎矩以及應力的數值解與解析解。在圖8中，彎矩數值解最大值80.4 N·m，解析解最大值83.6 N·m，相對誤差為4.0%.圖9給出的應力數值解最大值6.998 MPa，解析解最大值7.262 MPa，相對誤差為5.3%.圖10、圖11給出了全程下梁彎矩以及應力隨時間和位置的變化。

圖11 下梁應力隨時間和位置的變化曲面

由圖4、圖5、圖8、圖9可以看出，數值解與解析解的最大值比較接近，且都發生在0～0.5 m范圍之內，而后解析解出現了波動，是由于在雙層彈性梁模型的解析解求解時未考慮層間阻尼造成的。同時，對比上、下梁的動態響應值，上梁的響應值明顯高于下梁的，表明電磁軌道比外層壁板受移動荷載影響要大。通過圖4、圖5、圖8和圖9中兩種解法結果的對比，不難發現解析解與數值解吻合得比較好。

6 結論

本文建立了方型電磁發射裝置的雙層彈性基礎懸臂梁模型，分別采用Heaviside函數和Dirac函數建立導軌及壁板的動力學微分方程，用解析法求解其在工作狀態下的動態響應，并使用數值法求解與之進行比較。得到以下結論：

1)雙層彈性懸臂梁動態響應的解析解與數值解存在一定的差異，但結果總體較為吻合，解析解的可靠性在一定程度上通過其與數值解的對比得到了驗證。

2)對于雙層懸臂梁模型的電磁炮，軌道動態響應比外壁板的響應大，而且峰值基本位于0～0.5 m之內，在進行電磁炮設計時，應注意軌道及其固定端的加強。

3)本文建立的雙層彈性懸臂梁模型及導出的動態響應的解析解，能夠幫助完善電磁軌道發射裝置的理論研究，并可供相關領域的工程設計計算參考。