科學“睡美人”現象研究

李品保 王幼軍

摘要：以CNKI數據庫1892—2009年數學史主題1952篇論文為研究對象，采用嚴格的“睡美人”指標對其進行檢索，對識別出的“睡美人”論文的基本概況、存在原因進行具體分析，并進一步對“睡美人”現象在不同領域論文中的存在原因、表現程度作差異分析。研究發現，“睡美人”現象在數學史主題論文中表現可能更為明顯；即使是權威發表論文也可能被忽視。

關鍵詞：“睡美人”；延遲承認；數學史；數學教育

中圖分類號：G301文獻標識碼： ADOI：10.3969/j.issn.1003-8256.2020.04.012

開放科學（資源服務）標識碼（OSID）：

1問題的提出

科學界存在認識延遲的現象：科學成果發表初期幾乎無人關注，過了一段時間后又突然吸引大量關注并為科學界所承認，這種現象被稱為“阻滯發現”“延遲承認”等。在學術論文中表現為一篇論文發表后多年內幾乎無人或很少人關注，獲得零被引或低被引；在一段時間后又突然受到大量關注，獲得較高被引或高被引，而這種論文又對該領域研究有較重要的影響，這種遭遇“延遲承認”的論文被稱為“睡美人”論文。“睡美人”論文最早由荷蘭萊頓大學科學技術研究中心（CWTS）的Anthony F. J. van Raan[1]于2004年的一篇名為“科學中的睡美人”中提出。他稱那些發表后相當長的一段時間內幾乎不被任何人關注，就像格林童話中的“睡美人”一樣在沉睡，在某個時刻又突然吸引很多人注意的論文為“睡美人”論文，喚醒“睡美人”論文的論文則被稱為“王子”論文（Prince Literature）。“睡美人”論文動態地反映了引文的時間特征和歷史過程，是從文獻計量學的角度定量地描述了科學領域中的“延遲承認”現象。

早期學者多是從科學史的角度對“睡美人”進行不系統的研究，隨著研究方法的系統化，人們重新發現并肯定了物理、化學等領域“睡美人”論文的價值，關于“睡美人”的研究也逐漸升溫。迄今最大規模的“睡美人”論文研究對1900年以來Web of Science收錄的發表在自然科學及社會科學領域2000多萬份被引次數至少為1次的論文進行系統分析后發現，物理學、化學和數學中的“睡美人”論文最多[2]；S. Redner[3]研究了Physical Review期刊上近110年具有“睡美人”特征的文獻；梁立明等[4]曾對一篇被遲滯承認的超弦理論論文進行研究；杜建等[5]利用被引速率指標研究了2014年諾貝爾化學獎得主Stefan Hell的“睡美人”文獻。姚建文等[6]研究了我國CSSCI中圖書情報學領域中的“睡美人”文獻；袁紅等[7]研究了國內圖書情報學、物理學及醫學三大學科領域“睡美人”文獻，等等。國際上關于“睡美人”文獻的研究成果比較豐富，在研究方法、研究對象的選擇上已經十分成熟；國內“睡美人”研究在學者們的共同努力之下也漸趨成熟，尤其擅長追蹤“熱點”研究或對“熱點研究”進行研究，但距系統研究國內所有科學領域中可能存在的“睡美人”文獻的目標仍有較大距離。

本文將通過“睡美人”視角去審視及評析國內數學史主題論文中可能存在的曾被忽視但對該領域影響較大的研究成果，試圖回答以下問題：相比物理學、醫學等熱門研究領域，以數學史為主題的“冷門”研究中是否也存在“睡美人”？存在原因具體是什么？因其“冷門”屬性，“睡美人”論文在這一主題領域和其他領域中的存在原因、具體表現是否一致？

2研究設計

2.1已有研究方法

學界目前廣泛采用的有兩種研究方法，第一種是van Raan在“科學中的睡美人”一文中給出的界定“睡美人”論文的三項指標：沉睡時長（length of the sleep），即論文處于零被引或低被引狀態的時間，他在文中考察了沉睡時長為5到10年的案例；沉睡深度（depth of sleep），即按照論文在考察的沉睡時長內，年均被引1次及以下稱為深度沉睡（deep sleep），年均被引1到2次稱為沉睡（less deep sleep）；喚醒強度（awake intensity），即論文在緊接睡眠期之后的4年內被引用次數（不包括自引），這4年被稱為喚醒時期（awaking period）。喚醒強度還可以分為5個等級：（21，30），（31，40），（41，50），（51，60），（60<）。van Raan曾按照一個比較嚴格的閾值，即論文發表后10年內年均被引次數不超過1次，被喚醒后10年內年均被引次數要大于5次，來識別物理學、化學、工程學與計算機科學領域的“睡美人”論文[8]。

其中Cn是論文在考察期內的總被引次數，Ci是第i年的被引次數，n是論文的年齡。被引速率的值越小，則其前后時段被引頻次的差異性越大，說明論文的“睡美人”特征越明顯。有學者在此基礎上以被引速率0.4、0.5和0.6為分界點，將論文分為：延遲承認型（CS<0.4）；曇花一現型（CS>0.6）；厚積薄發型（0.4

2.2研究方法

van Raan[1]的三項指標屬于主觀指標，Wang J[9]提出的被引速率屬于客觀指標，均存在一定局限性[11]。本文引入van Raan界定“睡美人”論文的三項指標，結合論文發表后需經10年被引、沉睡時長需大于等于5年、被引速率閾值設定為0.4、總被引次數排該主題文獻前1%為高被引文獻等指標，最終確定本文所研究的“睡美人”論文必須同時滿足6個指標：

a.屬于高被引文獻；

b.被引速率小于0.4；

c.年齡大于等于10年；

d.沉睡時長大于等于5年；

e.睡眠期內年均被引次數小于等于2；

f.被喚醒后4年內總被引次數大于等于21。

以CNKI中國學術期刊網絡出版總庫為數據源，采取綜合識別指標檢索自1892年至2009年“數學史”主題共1952篇論文，識別出唯一一篇同時滿足以上6個條件，具有“睡美人”特征的論文。該文于1994年發表于《數學教育學報》，題目為《數學哲學、數學史與數學教育的結合—數學教育改革的一個重要方向》[12]（以下簡稱《數學教育改革》），作者為徐利治先生、王前先生。

3結果分析

3.1基本概況

從表1看出：截至2019年10月，該文在CNKI數據庫數學史主題共4455篇論文中總被引次數排名第6，總被引次數排該主題論文約前0.13%，高于目前多采用的排前1%為高被引論文的標準，屬于高被引論文。

本文所檢出“睡美人”論文《數學教育改革》的詳細信息整理見表2。從表2可知，此文的沉睡強度可以分為兩個時間段：1994—1998年，該論文年均被引次數（不含二級引證文獻數量）為0.8，沉睡強度為深度沉睡；1994—2005年，該論文年均被引次數約為1.6，沉睡強度為沉睡。該文的喚醒強度位于（21，30）區間，屬于最低等級。

3.2存在原因分析

此文在發表后12年內一直處于沉睡期，但從之后的引用表現來看此文在該領域的研究又扮演著重要角色。那么，該論文之所以遭遇延遲承認成為“睡美人”的原因是什么？可以從兩個方面具體分析。

3.2.1未獲得及時關注的原因

第一，該文研究內容涉及多學科，不能及時獲得廣泛承認。以“數學史”為主題的研究總共可為兩大類：一是著重于數學史本身，分析國內外數學史研究現狀或趨勢等，如表1中排名14的《中國數學史研究范式的轉換》；二是將數學史與數學教育相結合，著重于討論數學史對數學教育產生的影響等等，如本文所討論的《數學教育改革》。

1972年第二屆國際數學教育大會上，數學史與數學教學關系國際研究小組（HPM）成立，標志著數學史與數學教育的關系正式成為一個學術研究領域[13]。《數學教育改革》則是在國內外數學教育界對數學史和數學哲學的興趣逐漸升溫的背景下誕生的。作者認為需要從理論上和實踐上對這種趨勢進行分析研究，從而使這種教育改革得以深入、持久地展開下去。作者提議在數學教育中引進新的教學手段和方法，把數學史和數學哲學的研究成果運用于數學教育過程之中，力促數學的哲學、歷史和教育三者的有機結合，將研究視野擴展到了多個學科。該論文屬于國內相關研究領域較早的一批研究之一。此外，作者還從數學本體論、認識論和方法論三個方面談論將數學哲學研究成果運用于數學教育中，認為對培養學生的數學思維能力有重要幫助；重視數學史對教育的作用，尤其是“外史”方面，而“外史”研究的內容涉及教育、哲學、宗教和社會等方面，需要從多學科的視域來考察數學與社會生活各方面的關系。

該文于1994年發表后引起了國內極少數學者的注意，但數學史及數學哲學等對數學教學的意義并沒有得到及時的廣泛承認，這意味著要求該領域的研究學者必須同時具備一定的數學、教育學、歷史學和哲學等知識，這在增大相關學者研究難度的同時，也提高了相關學界的評價難度，最終無法獲得學術界的廣泛理解。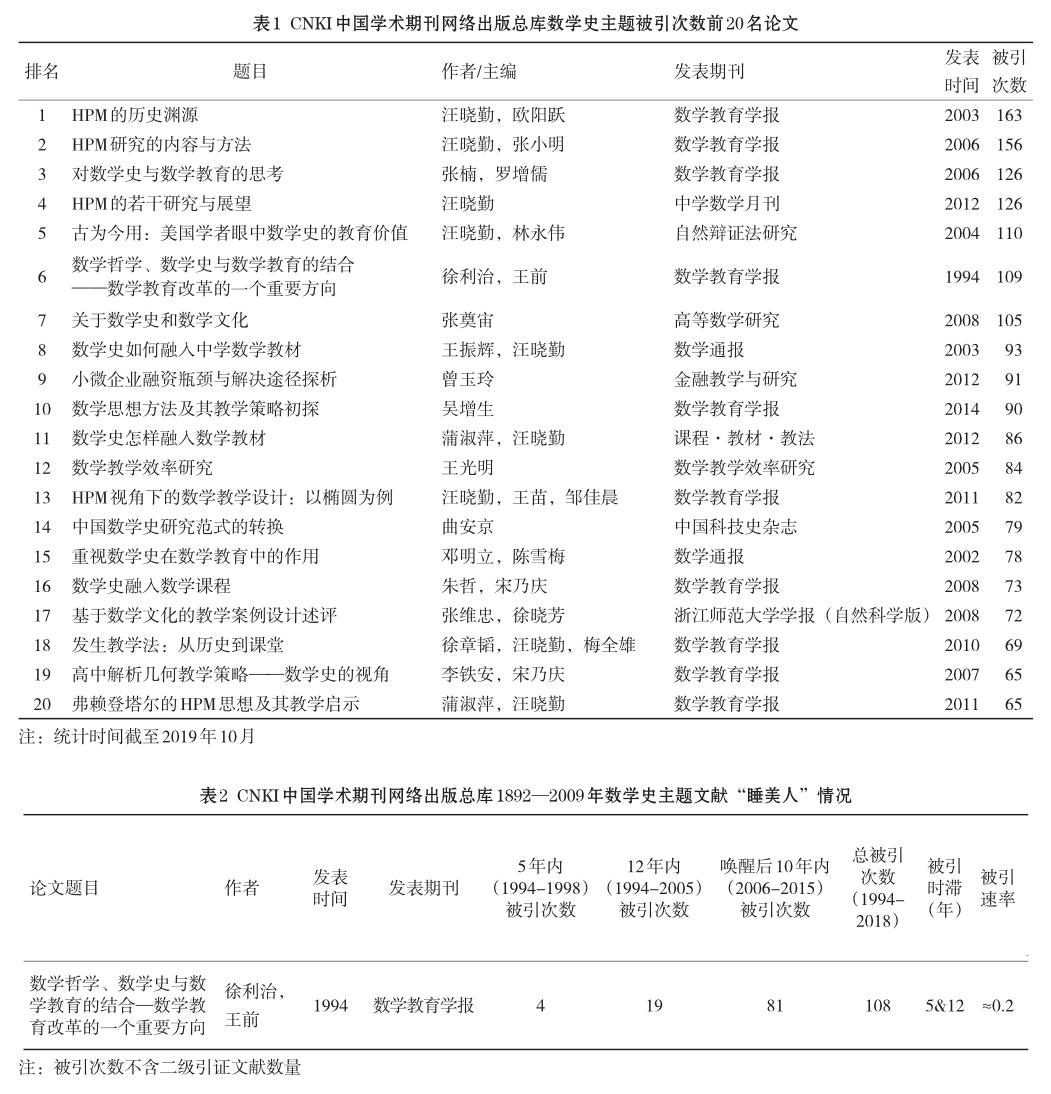

第二，發表越早，面臨傳統阻礙越多。《數學教育改革》一文是自1892年始CNKI中國學術期刊網絡出版總庫數學教育主題論文中最早在題目和內容上明確提出要將數學史、數學哲學與數學教育結合起來的論文。此外，該文發表于20世紀90年代，而學界當時仍在對自20世紀60年代以來關于“新數學”教育是非功過進行爭論。該文借鑒國外先進教育經驗，重新審視了這場爭論，認為這些爭論也是在數學史和數學哲學的背景下進行的。

一方面該文早于1994年就已發表，從這點來看，該文可以搶得先機，更早獲得學界關注，被引時間也更長；但從另一方面來看，越早發表就意味著可能面臨越多傳統的阻礙，不能獲得學界及時認可的可能性也就越大。

3.2.2得到重視的原因

第一，研究熱點的興起。自從2005年第一屆全國數學史與數學教育研討會召開以后，數學史在數學教育中的作用日益受到關注[14]。從表2可知，該文于1994年發表后5年內處于深度沉睡，12年內處于沉睡，并未及時獲得當時科學界的較多關注。從圖1可見，該文2005年被引5次，2006、2007年更是都達到9次被引。正是由于國內自2005年起數學史在數學教育中的作用研究成為熱點，該文才突然得到大量關注，從而于當年被喚醒得以成為真正的“睡美人”論文。

第二，基于發表期刊的權威性。《數學教育學報》創刊于1992年，由中國教育學會和天津師范大學主辦，是目前國內數學教育領域最高層次的學術期刊。另外，從表1可知，CNKI數據庫中數學史主題被引次數前20名論文中，有10篇發表在《數學教育學報》上，可見該研究領域的學者對該期刊的認可度之高，該刊發表的論文在該研究領域的影響之大。這也是該文之所以能在幾年甚至幾十年后仍受到較多關注，從較低被引到高被引的重要原因之一。

第三，論文質量過硬。首先，上文提到的該文未獲得及時關注但如今卻成為高被引論文說明該文具有前瞻性等重要價值；其次，提出的建議可操作性強。該文結合現實熱點問題和教育需求，在討論將數學哲學、數學史融入數學教育的重要意義和將三者結合起來實施的困難后，還提出了五項頗具建設性的具體措施，比如在高等教育中增加了數學哲學和數學史方面的內容以培養師資；新編含數學哲學和數學史相關成果的數學教材；開展三者結合的學術活動等等，這些措施如今均已得到有效實施并取得良好效果；最后，影響深遠。該文作為被引速率低的高被引論文說明了該文的學術生命力強，而論文的學術生命力越強，對該研究領域的學術貢獻可能越大，該文至今在同研究領域文獻中仍受到持續關注和引用。當然，論文質量過硬正是“美”之所在。

3.3差異分析

將“睡美人”現象在數學史主題領域和其他領域中的存在原因、表現程度作以下差異分析：

3.3.1存在原因差異分析

權威發表論文同樣面臨被忽視的可能。有學者研究發現，van Raan識別出的“睡美人”論文的作者L.J. Romans發表論文時剛博士畢業不久，為該領域的一名新秀，因此認為人們只會更多關注權威們的工作而不會引用新秀的論文。本文所識別出的“睡美人”論文《數學教育改革》的第一作者為徐利治先生，徐先生是中國著名數學家、數學教育家和數學哲學家，其在數學研究、數學哲學和數學教育方面均做出了創造性的貢獻[15]。在該文發表前，徐先生曾擔任大連理工大學應用數學研究所所長、中國組合數學研究會第一任理事長等職，已發表多篇關于數學研究、數學教育等方面的重要論文。即使像徐先生這樣的權威發表論文同樣可能被忽視，這說明“睡美人”論文之所以“沉睡”的主要原因可能并不在于作者本身，即并非“名聲不夠”，而可能在于論文的內容涉及面、發表時間等，即所謂“生不逢時”。

3.3.2表現程度差異分析

有學者曾對“睡美人”現象在圖書情報、醫學和物理學領域中的表現作對比研究，研究發現“睡美人”現象在這三個領域中表現明顯程度依次降低。而一般認為圖書情報領域相比醫學、物理學領域來說更為“冷門”，由此可推測，“睡美人”現象在相對“冷門”領域中表現可能更為明顯。經本文案例研究，可得以下兩點具體差異表現：

存在概率正常偏大。從截至目前有關“睡美人”論文大規模的分析來看，在嚴格的指標界定下“睡美人”論文的正常比例約為萬分之一到千分之一[8]，總體來說是較罕見現象。本文以嚴格的指標（6個條件）對數學史主題論文進行篩選，在1952篇論文中發現1篇“睡美人”論文，“睡美人”現象存在概率為1/1952，屬于正常范圍，但不可否認的是“睡美人”現象在國內數學史主題論文中存在的概率在正常范圍內偏大。

沉睡時長可能更長。該研究還發現在這三大領域中“睡美人”論文在沉睡期間的平均沉睡時長依次遞減，分別為10、8.45、7.78。本文在數學史主題論文中只發現一篇符合本文嚴格條件的論文，平均沉睡時長為12，可以看出“睡美人”論文在國內數學史主題這類“冷門”領域中沉睡時長可能更長。

經分析，可以認為“睡美人”現象在數學史主題論文中表現可能更為明顯。

4結語

首先，“睡美人”在數學史主題論文中存在。

其次，與其他熱門領域如物理學、醫學等相比，“睡美人”現象在數學史主題一類的“冷門”研究領域中的表現更為明顯，具體表現為存在的概率正常偏大、沉睡時長可能更長。

再次，“睡美人”現象在數學史主題論文中存在的原因可以從“未獲得及時關注”和“得到重視”兩個方面來具體分析。存在原因與之前研究所得原因也并非完全一致，從本文研究來看，主要原因并非作者“名聲不大”等，即使是權威發表論文同樣面臨被忽視的可能，而是因為論文“生不逢時”。

最后，本文采取嚴格條件進行篩查的目的是為了分析國內數學史論文中可能存在的“睡美人”特征最為明顯的文獻，但是，這樣也不可避免地忽視了較高被引中可能存在的具有重大意義的論文。此外，在國內其他數據源中數學史主題研究領域的“睡美人”論文存在情況如何？書籍中是否也存在“睡美人”？這都有待更多的實證分析。

參考文獻：

[1]VANRAAN A FJ.SleepingBeautiesinscience[J]. Scientometrics， 2004， 59（3）： 467-472.

[2]WANG J， MA F， CHEN M， et al. Why and how can" sleeping beauties" be awakened？[J]. The Electronic Library， 2012， 30（1）： 5-18.

[3]REDNER S. Citations statistics from 110 years of physical review[J]. Physics Today， 2005， 58（6）： 49-54.

[4]梁立明，林曉錦，鐘鎮，等.遲滯承認：科學中的睡美人現象：以一篇被遲滯承認的超弦理論論文為例[J].自然辯證法通訊， 2009， 31（1）： 39-45.

[5]杜建，武夷山.基于被引速率指標識別睡美人文獻及其"王子"——以2014年諾貝爾化學獎得主Stefan Hell的睡美人文獻為例[J].情報學報， 2015， 34（5）： 508-521.

[6]姚建文，趙慶華，吳麗萍.圖書情報論文的睡美人現象考察[J].大學圖書館學報， 2014， 32（3）： 64-68.

[7]袁紅，杭培培.不同學科領域"睡美人"論文的比較分析[J].情報資料工作， 2016， 37（2） ： 34-38.

[8]杜建，武夷山. "睡美人"論文的重要特征、預測線索與政策啟示[J].科學學研究， 2018， 36（11）： 1938-1945.

[9]WANG J. Citation time window choice for research impact evaluation [J]. Scientometrics， 2013， 94（3）： 851-872.

[10]杜建，武夷山.睡美人與王子文獻的識別方法研究[J].圖書情報工作， 2015， 59（19）： 84-92.

[11]開濱，姚艷玲.自然科學領域中睡美人文獻跨學科特征實證研究——以SCI中6大學科為例[J].情報雜志， 2018， 37（8）：145-152.

[12]徐利治，王前.數學哲學、數學史與數學教育的結合——數學教育改革的一個重要方向[J].數學教育學報， 1994， 3（1）： 3-8.

[13]汪曉勤，歐陽躍. HPM的歷史淵源[J].數學教育學報， 2003， 12（3）： 24-27.

[14]沈中宇，鄒佳晨，汪曉勤. ICME-13之HPM專題研究綜述[J].數學教育學報， 2017， 26 （5） ： 71-76.

[15]沈威.徐利治數學教育思想研究[J].數學教育學報， 2019， 28（1）： 74-78.

Study on the Phenomenon of "Sleeping Beauty"： Centered with the Thesis in the Subject of History of Mathematics

LI Pinbao，WANG Youjun（ College of Philosophy， Law & Political Science，Shanghai Normal University， Shanghai 200234，China）

Abstract： Based on CNKI database， 1952 papers in the subject of history of mathematics from 1892 to 2009 were searched by using strict identification index of "sleeping beauty". To analyzes the basic situation， existing reasons of the identified"sleeping beauty" papers， and further analyzes the existing reasons and performance degree of "sleeping beauty" phenomenon in different fields. It is found that the phenomenon of "sleeping beauty" may be more obvious in the subject of history of mathematics， and even the authoritative papers may be ignored.

Keywords： "sleeping beauty"；delayed recognition；history of mathematics；mathematics education