二維太赫茲光子晶體能帶結構研究

劉榮青

摘? 要：文章應用平面波法和時域有限差分法研究了二維太赫茲光子晶體TM模能帶結構。研究發現，當晶格常數a=100×10-6m，介質柱半徑R=0.3a時，可以得到TM模式下THz波段的最佳能帶結構。此研究結果對高速率、超寬帶THz通信系統的發展具有重要的指導意義，為太赫茲波器件的開發提供重要理論依據。

關鍵詞：太赫茲;二維光子晶體;平面波法;時域有限差分法;禁帶

中圖分類號：O734? ? ? ? ?文獻標志碼：A? ? ? ? ?文章編號：2095-2945（2020）07-0009-03

Abstract： In this paper， plane wave method and finite-difference time-domain method are used to study the band structure of TM mode of 2D terahertz photonic crystal. The study found that when the lattice constant is 100×10-6m and the dielectric column radius is 0.3a， the best band structure of THz band in TM mode can be obtained. This research result has important guiding significance for the development of high-speed， ultra-wideband THz communication systems， and provides an important theoretical basis for the development of terahertz wave devices.

Keywords： terahertz; two-dimensional photonic crystal; PWM; FDTD; band gap

引言

太赫茲（THz）指的是輻射區域處在波譜中微波波段與紅外波段之間，頻率從0.1-10THz的電磁波[1]。THz波擁有頻譜范圍寬、容量大、穿透性好、傳輸速度快等優點[2]，人們預言它在物理、醫學、生物、材料乃至軍事等方向上存在潛在的研究價值。THz波的高帶寬性能使其在快速進步和發展的無線通信方面也具有非常廣闊的發展前景[3]。因為THz波在自由空間中傳播時的能量損耗較大，所以如何研究出便于操控THz波傳輸并且有利于各個器件之間連接和耦合的波導型功能器件非常關鍵。在探索無線通信發展的過程中，波導型功能器件也展示出了舉足輕重的作用。光子晶體[4]作為一種由不同介電常數的介質在空間中周期性排布而構成的新型人造材料，形成了一定的光學禁帶和通帶。光子晶體發生布拉格散射形成了禁帶，禁帶頻率范圍內的光波無法在此結構中傳輸。假如破壞晶體的結構，形成了缺陷態，就可以很好地局域某些頻率的電磁波。另外，在微波和紅外光之間，THz波段的光子晶體較紅外波段的光子晶體更容易制作，較微波波段的光子晶體更便于集成[5]。

本文結合“光子晶體”與“太赫茲”兩大光學研討熱門領域，運用平面波方法[6]和時域有限差分方法，通過模擬軟件對光子能帶結構進行模擬計算，為實際制作二維太赫茲光子晶體的波導結構提供了模型參照。

1 能帶計算理論分析

1.1 平面波法

在光子晶體能帶結構計算的理論研究中，平面波法（PWM）不僅是最廣泛應用的，而且還是最早使用的計算方法。其主要思想是首先把光子晶體中傳播的電磁波展開為一系列平面波疊加的形式，同時按照相同的方式也把光子晶體的介電常數進行處理，然后代入Maxwell方程組，把它轉換為本征方程，求解出來以后就可以獲得本征頻率和本征模態，從而確定光子晶體的禁帶大小。PWM法的缺點是收斂速率不夠快，在求解含有缺陷的光子晶體禁帶時，通常會因為計算能力受到局限而很難得到高效準確的禁帶范圍。

1.2 時域有限差分法

時域有限差分法（FDTD）在1966年由Kane S.Yee提出，近些年，隨著計算機計算能力的快速提升，FDTD法被逐漸普遍應用在電磁場的數值計算中。它的主要原理是在時間和空間上將電磁場的E、H分量采用交替抽樣的離散方式，把Maxwell方程在Yee氏網絡空間中直接換算為差分方程，隨著時間的推移逐步求取時間軸上空間各個網格點的電磁場。時域有限差分方法計算得到空間格點的勢場等量，經過傅里葉變換后就可以得到布里淵區邊界上的特征頻率，這些頻率的集合就是能帶結構。由于在差分方程中被模擬空間電磁性質的參數是按照空間網格確定的，因此，只要在相應空間網格點設置合適的參數即可高精度且高效模擬非均勻性和非線性介質結構。FDTD方法的優勢在于簡單、直觀，并且易于編程，使用這種方法能夠減少計算機的計算量和內存。此外，FDTD法不僅可以研究完整均勻的光子晶體，而且可以研究缺陷態，這是它和PWM法最大的不同之處。

2 仿真結果及討論

2.1 完整二維光子晶體仿真模型

正方形晶格排列的完整二維光子晶體仿真模型如圖1所示，TM模式，采用19×19的介質柱分布在真空中，實際仿真參數設置如下：介質柱半徑用R來表示，晶格常數a=100×10-6m，即100μm。介質柱材料選用與半導體集成工藝兼容性良好的高阻硅。這是由于高阻硅在微波與紅外之間的太赫茲波段幾乎是透明的，具備較高的介電常數（11.7）和較低的吸收系數（大約為0.04cm-1）。選用高阻硅作為二維光子晶體的材料還有一個重要原因是由于硅技術是現階段相對來說比較先進和成熟的半導體技術[7]，實際制作起來相對于其它材料稍微容易一些。

2.2 完整二維光子晶體能帶計算

運用PMW法，使用matlab軟件，求解完整二維光子晶體的能帶。從實際的角度來講，計算得到的光子晶體的禁帶頻率范圍越寬，光子晶體的結構性能就越優勝。其它結構參數保持不變，將介質柱半徑R增大或者減小的時候，禁帶寬度會隨著占空比的變化有所改變，如圖2所示。圖2（a）為R=0.2a時TM波的能帶圖，圖2（b）為R=0.3a時TM波的能帶圖，圖2（c）為R=0.4a時TM波的能帶圖，歸一化頻率的表達式為ωa/c。從圖2（a）、2（b）、2（c）中可以很清楚地看出不同R的光子晶體能帶結構中均含有三條禁帶，其中中間那條禁帶最寬，上面那條禁帶最窄，研究光子晶體傳輸特性一般選擇最寬的禁帶來進行討論。R=0.2a時最寬禁帶的歸一化頻率范圍約為0.4532-0.5258，R=0.3a時最寬禁帶的歸一化頻率范圍約為0.4245-0.5076，R=0.4a時最寬禁帶的歸一化頻率范圍約為0.4028-0.4744。通過比較得知，R=0.3a時TM波禁帶寬度最寬，能帶圖是最佳的，其禁帶范圍分別為0.7102-0.9062THz、1.2735-1.5228THz、1.9662-2.0544THz。

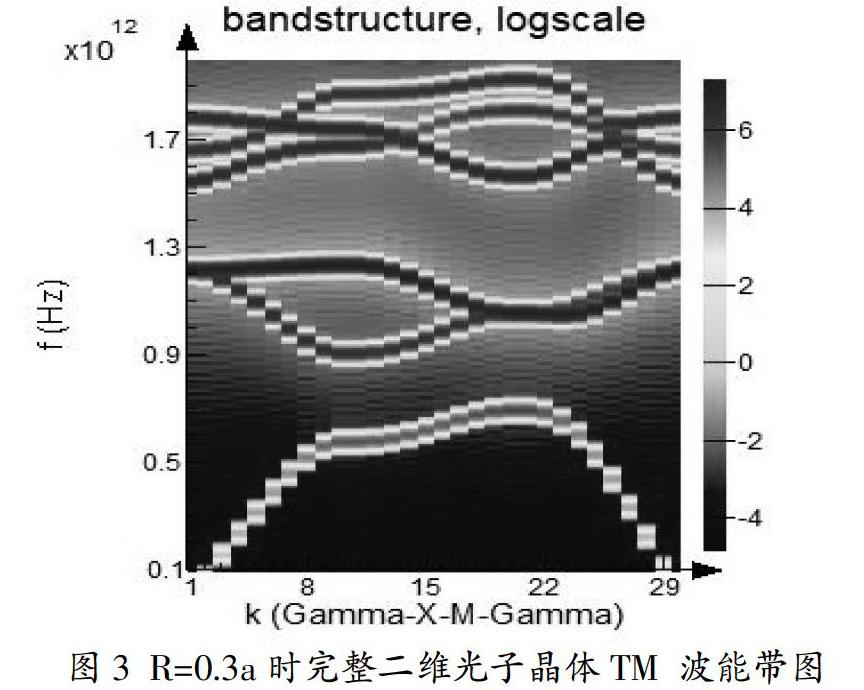
由于使用PWM法難以精確求解含有缺陷的二維光子晶體的能帶，接下來采用FDTD方法研究兩種缺陷態。利用FDTD Solutions軟件建模仿真，分析研究缺陷態光子晶體的能帶結構。首先計算了R=0.3a時完整二維光子晶體TM波的能帶結構，如圖3所示。從圖3中可以看出，完整二維光子晶體TM波禁帶范圍大約為0.7139-0.8572THz、1.2705-1.5119THz、1.9872-2.0318THz，和采用PWM法得到的結果接近，從而驗證了采用FDTD法計算二維赫茲光子晶體能帶結構的可行性。

3 結束語

本文將平面波法與時域有限差分法應用于二維光子晶體能帶結構計算，材料選用19×19二維正方晶格硅介質柱分布在空氣中，晶格常數a=100×10-6m，當介質柱半徑R=0.3a時，可以得到TM模式下THz波段的最佳能帶結構。此研究為制作太赫茲光子晶體器件提供重要理論依據，對高速率、超寬帶THz 通信系統的發展具有非常重要的參考價值[8]。

參考文獻：

[1]徐景周，張希成.太赫茲科學技術和應用[M].北京：北京大學出版社，2006.

[2]Greenland P T. Principles of Terahertz Science and Technology[M]. 2009.

[3]Federici J， Moeller L. Review of terahertz and subterahertz wireless communications[J]. Journal of Applied Physics， 2010， 107（11）：6-323.

[4]Joannopoulos J D，Johnson S G，Winn J N， et al. Photonic Crystals： Molding the Flow of Light[M].Princeton：Princeton University Press，2011：30-90.

[5]Lin S Y， Fleming J G， Hetherington D L， et al. A three-dimensional photonic crystal operating at infrared wavelengths[J]. Nature， 1998， 394（6690）： págs. 251-253.

[6]Guo S P， Albin S. Simple plane wave implementation for photonic crystal calculations[J]. Optics Express， 2003， 119（2）： 167-175.

[7]張偉，王智勇，王文超，等.基于光子晶體耦合波導的寬帶慢光研究[J].光學學報，2012，32（2）：162-166.

[8]Ho-Jin Song， Nagatsuma T. Present and Future of Terahertz Communications[J]. IEEE Transactions on Terahertz Science and Technology， 2011， 1（1）：256-263.