疊積式油浸鐵芯串聯(lián)電抗器電抗值偏差及控制措施探討

張燕華　顏紅岳　王小娟　沈鈺偉

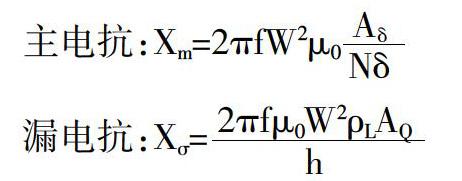
摘? 要：文章重點(diǎn)闡述了鐵芯電抗器中氣隙的重要性及電抗值在設(shè)計(jì)及制造過程中的注意事項(xiàng)，通過參數(shù)的經(jīng)驗(yàn)設(shè)計(jì)、部件加工的偏差控制、試驗(yàn)的預(yù)期調(diào)試等方法最終達(dá)到電抗值偏差控制的效果。

關(guān)健詞：鐵芯電抗器;電抗值;偏差;磁阻

中圖分類號(hào)：TM47? ? ? ? ?文獻(xiàn)標(biāo)志碼：A? ? ? ? ?文章編號(hào)：2095-2945（2020）07-0129-03

Abstract： This paper focuses on the importance of the air gap in the iron core reactor and the matters needing attention in the design and manufacture of the reactance value. The effect of reactance deviation control is finally achieved by means of empirical design of parameters， deviation control of component processing， expected debugging of test and so on.

Keywords： iron core reactor; reactance value; deviation; magnetoresistance

前言

電抗器又被稱作電感器，是一種動(dòng)態(tài)能量存儲(chǔ)元件，當(dāng)電路工作于不同的模式下，電抗器不僅起到存儲(chǔ)電能的作用，同時(shí)也可釋放所存儲(chǔ)的電能。當(dāng)電抗器與電容器串聯(lián)時(shí)，起到限制合閘涌流及抑制諧波的作用。為了限制合閘涌流，一般配置電抗率1%的串聯(lián)電抗器。但當(dāng)系統(tǒng)中含有高次諧波，就要配置不同電抗率的電抗器，電網(wǎng)背景諧波為五次及以上時(shí)，這時(shí)一般配置電抗率為5%的電抗器，電網(wǎng)背景諧波為三次及以上時(shí)，這時(shí)一般配置電抗率為12%的電抗器，這樣不僅可以限制合閘涌流同時(shí)還可以抑制諧波。

電抗值選定在無(wú)功補(bǔ)償裝置中起到至關(guān)重要的作用。尤其對(duì)于串聯(lián)電抗器來(lái)說(shuō)，電抗值一旦偏離范圍，就有可能造成諧振，后果極其嚴(yán)重。電抗率為5%的電抗器，用以抑制5次諧波，它的諧振頻率為223Hz，離5次諧波頻率250Hz較近。而電抗率為12%的電抗器，用以抑制3次諧波，它的諧振頻率為144.5Hz，離3次諧波頻率150Hz則更近。這時(shí)電抗值的偏差控制在電抗器設(shè)計(jì)值中更是重中之重。對(duì)于鐵芯電抗器來(lái)說(shuō)，受到磁性材料本身特性的影響，電抗值會(huì)隨著磁導(dǎo)率變化而變化，此時(shí)需要引入氣隙，本文先從鐵芯電抗器引入氣隙的意義論述，再介紹35kV及以下疊積式油浸鐵芯串聯(lián)電抗器是如何在設(shè)計(jì)及制造過程中保障電抗值達(dá)到預(yù)期要求的。

1 鐵芯電抗器引入氣隙的意義

磁阻與材料的相對(duì)磁導(dǎo)率相關(guān)。應(yīng)用于磁性材料中的磁場(chǎng)強(qiáng)度是非線性的。無(wú)氣隙時(shí)，磁通被限制在磁心內(nèi)部，一個(gè)具有足夠多匝數(shù)的小電流線圈就很容易使磁心飽和。有氣隙時(shí)，由于氣隙的磁阻遠(yuǎn)大于磁心磁阻，此時(shí)氣隙中的磁場(chǎng)強(qiáng)度比磁心內(nèi)部的磁場(chǎng)強(qiáng)度大的多，同時(shí)能量大部分被存儲(chǔ)在氣隙中。因而提高了系統(tǒng)的儲(chǔ)能能力，這時(shí)將需要更大的電流才能使磁心飽和。

我們知道，在磁學(xué)中磁導(dǎo)率μ代表材料導(dǎo)通磁通的能力，是磁通密度B對(duì)磁場(chǎng)強(qiáng)度H的比值，即μ=B/H。在給定磁感應(yīng)強(qiáng)度的情況下，磁導(dǎo)率體現(xiàn)的是磁性材料能夠被磁化到這個(gè)磁感應(yīng)強(qiáng)度難易程度。一方面，具有高磁導(dǎo)率的磁性材料對(duì)溫度、壓力、勵(lì)磁電壓和頻率都很敏感;另一方面，電感的變化與磁導(dǎo)率的變化成正比，同時(shí)電感的變化將對(duì)勵(lì)磁電流有影響。因而電抗器應(yīng)該有一個(gè)穩(wěn)定的磁導(dǎo)率即等效磁導(dǎo)率μeff。把氣隙引入磁路中，將獲得減小并且穩(wěn)定的等效磁導(dǎo)率。

假定氣隙長(zhǎng)度為g，分布的整個(gè)磁心的長(zhǎng)度為L(zhǎng)c，那么磁心的等效磁導(dǎo)率將由μr（相對(duì)磁導(dǎo)率）減小到等效磁導(dǎo)率μeff。當(dāng)相對(duì)磁導(dǎo)率μr>>1時(shí)μeff≈Lc/g。由于氣隙的引入，使得等效磁導(dǎo)率大大降低，這樣最大磁通密度Bm可以達(dá)到飽和磁通密度Bs。由于氣隙存在，隨其面積的增加，帶氣隙磁心所存儲(chǔ)的能量也隨之增加，大多數(shù)磁性材料特性隨著溫度、磁通量大小、樣式、廠家不同而不同。氣隙可以減少整體電感對(duì)這些參數(shù)的依賴，使電感值可計(jì)算性增加。氣隙滿足μeff<<μr，則與磁飽和、磁滯、矯頑力相關(guān)的問題都被弱化。總結(jié)帶氣隙磁心優(yōu)點(diǎn)：（1）磁飽和情況發(fā)生于更大的電流值出現(xiàn)時(shí)刻;（2）基于現(xiàn)有的電感量，能夠存儲(chǔ)更多的能量;（3）電抗值受不同磁心特性的影響變小。

當(dāng)包含固定氣隙的電抗器正常工作時(shí)，磁心中的磁感應(yīng)強(qiáng)度小于飽和值，此時(shí)電抗值是恒定的，并且該電感值由氣隙的長(zhǎng)度直接決定。通常設(shè)計(jì)的鐵芯電抗器氣隙采用分布式結(jié)構(gòu)。這樣做的優(yōu)點(diǎn)有：（1）單個(gè)氣隙減小，具有更小的邊緣磁通量;（2）電磁干擾影響將會(huì)下降;（3）邊緣效應(yīng)的線圈損耗將會(huì)減少;（4）當(dāng)達(dá)到飽和（μeff≈μr），磁心磁導(dǎo)率μ下降，導(dǎo)致電感值降低。由于氣隙是離散的，這樣影響會(huì)降低。因?yàn)榕c磁心初始磁導(dǎo)率相比，磁心固有磁導(dǎo)率會(huì)更高一些。

2 鐵芯電抗器額定電抗計(jì)算及氣隙分布

2.1 電抗值計(jì)算

當(dāng)鐵芯電抗器的線圈中通以交流電流時(shí)，它就產(chǎn)生兩部分磁通。一部分是主磁通φm，它沿鐵芯磁路（腳部鐵芯、氣隙、軛鐵）閉合，與全部線匝相交鏈;另一部分是漏磁通φσ，它主要沿空氣（或者油）閉合。主磁通所對(duì)應(yīng)的電抗稱為主電抗Xm，而漏磁通所對(duì)應(yīng)的電抗稱為漏電抗。

鐵芯電抗器的電抗XK為主電抗和漏電抗之和XK=Xm+Xσ。

根據(jù)電抗計(jì)算公式可以得出：當(dāng)頻率f、圈數(shù)W、鐵芯截面積Aδ確定后，能對(duì)電抗值進(jìn)行調(diào)整的部分只有氣隙長(zhǎng)度δ。可見，氣隙長(zhǎng)度成為電抗值精確度的關(guān)鍵。

按照電抗器設(shè)計(jì)程序分別計(jì)算出鐵芯截面積、線圈圈數(shù)、鐵芯氣隙總長(zhǎng)δ∑等參數(shù)。考慮電抗偏差范圍在（LA%～LB%），設(shè)計(jì)時(shí)電抗的目標(biāo)偏差值按照（LB%-LA%）/2偏差計(jì)算。因此，實(shí)際間隙總長(zhǎng)。

2.2 鐵芯柱中各個(gè)氣隙分布原則

根據(jù)氣隙中的磁阻可以看出，氣隙長(zhǎng)度越大，磁阻越大，磁場(chǎng)儲(chǔ)能越大。此時(shí)邊緣磁通也會(huì)增大。邊緣磁通將依氣隙的長(zhǎng)度向遠(yuǎn)離氣隙的方向擴(kuò)散。如果勵(lì)磁導(dǎo)線在磁心上并且包裹著氣隙，圍繞著勵(lì)磁導(dǎo)線產(chǎn)生的磁通將迫使邊緣磁通回到磁心中。因此，氣隙要求分布在有勵(lì)磁導(dǎo)線的部分。由于鐵芯柱中部磁力線較集中，而頭尾靠近軛部位置則開始發(fā)散，因此，每柱氣隙長(zhǎng)度分布以芯柱中間厚，兩邊薄為原則。由于氣隙附近的邊緣效應(yīng)，使鐵芯中向外擴(kuò)散的磁通一部分在進(jìn)入相鄰的鐵芯餅疊片時(shí)，與硅鋼片平面垂直，這樣會(huì)引起很大的渦流損耗，可能形成嚴(yán)重的局部過熱，所以鐵芯塊高度一般要求盡量低。單個(gè)氣隙長(zhǎng)度要小。

3 為保證電抗值，對(duì)氣隙及鐵芯組裝的工藝要求

3.1 氣隙板厚度偏差要求

在鐵芯組裝前，將每相氣隙板按照?qǐng)D紙要求全部疊裝放置在同一水平面上，并用C型夾固定，測(cè)量每相氣隙板總厚度，控制總厚度偏差在工藝規(guī)定偏差之內(nèi)，調(diào)整完畢后記錄三相氣隙板總厚度及調(diào)整氣隙板的厚度并標(biāo)識(shí)，以便組裝時(shí)不會(huì)混淆。

3.2 鐵芯加工及疊裝要求

鐵芯的不平整會(huì)增加氣隙，導(dǎo)致實(shí)際電抗值比設(shè)計(jì)電抗值偏大。因此，硅鋼片的加工尺寸要滿足圖紙要求，尺寸公差要滿足工藝要求;鐵芯的疊裝需要在平整度極高的平臺(tái)上完成，以保證鐵芯塊表面的平整度。

3.3 鐵芯柱總長(zhǎng)

為保證三相電抗值平衡，需要控制三相鐵芯總長(zhǎng)度偏差。工藝：在鐵芯組裝完成后，通過雙頭螺栓將上鐵芯與下鐵芯組裝并預(yù)加扭力后，測(cè)量三相鐵芯柱的總長(zhǎng)。控制三相鐵芯柱總長(zhǎng)在規(guī)定偏差內(nèi)。

3.4 鐵芯壓緊扭力要求

鐵芯與線圈的緊固方式通過雙頭螺栓來(lái)實(shí)現(xiàn)。線圈與鐵芯組裝后，逐步對(duì)稱施加扭力，以保證鐵芯受力的均勻性。

4 電抗值初步試驗(yàn)

4.1 初步測(cè)定電抗值試驗(yàn)（即產(chǎn)品裝箱前）偏差范圍指定

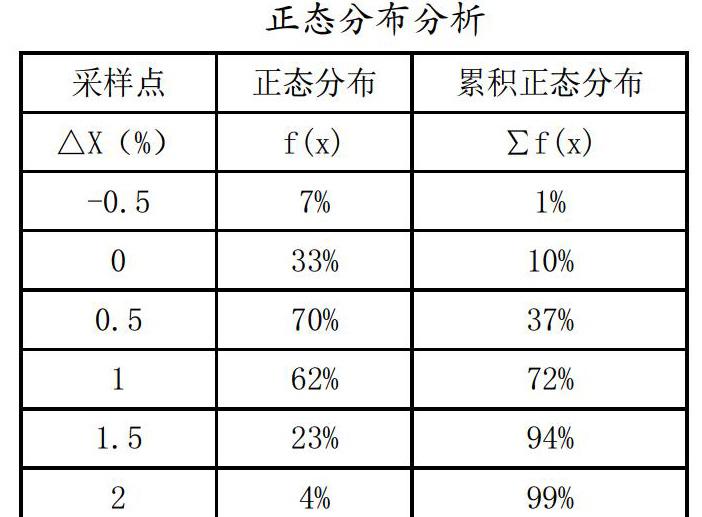
為確保成品電抗值在標(biāo)準(zhǔn)偏差范圍內(nèi)，對(duì)42臺(tái)初步測(cè)定電抗值與成品狀態(tài)電抗值偏差進(jìn)行比較，試驗(yàn)和分析數(shù)據(jù)見表1和表2，分布圖見圖1和圖2。

從圖1、圖2可知，△X（成品電抗值-初步測(cè)定電抗值偏差）主要集中出現(xiàn)在0～1.5%范圍內(nèi)，在-0.5～2%范圍內(nèi)，累計(jì)概率可達(dá)100%。以DL462-1992標(biāo)準(zhǔn)要求為例，電抗器成品狀態(tài)電抗值偏差范圍為0～5%，初步測(cè)定電抗值偏差為0.5～3%的范圍時(shí)，成品狀態(tài)電抗值合格率為100%。

4.2 電抗值初步試驗(yàn)

鐵芯與線圈組裝、接線完畢后，需在器身狀態(tài)進(jìn)行電抗的初步測(cè)定，試驗(yàn)前需對(duì)試驗(yàn)電源的三相一致性進(jìn)行檢查，防止由于電源的不一致性導(dǎo)致電抗的偏差不符合要求。

通過電抗測(cè)試，得到電抗的初步數(shù)據(jù)，如不符合初步電抗值判斷范圍，可按下述方法進(jìn)行調(diào)整：

（1）計(jì)算出三相電抗偏差的平均值

（2）計(jì)算調(diào)整后的氣隙總長(zhǎng)

（3）計(jì)算可變氣隙長(zhǎng)度

如果三相電抗值偏差超過±2%，需檢查三相電源的一致性及鐵芯組裝三相芯柱高度（含氣隙板）。芯柱高度檢查方法是：首先測(cè)量三相芯柱高度值是否偏差過大。如三相芯柱高度偏差在合理范圍內(nèi)，則通過在可調(diào)氣隙板間增加復(fù)印紙后，增緊壓力后，檢驗(yàn)復(fù)印紙的痕跡，來(lái)確定各相鐵芯的受力是否均勻。

5 結(jié)論

本文主要介紹了鐵芯電抗器電抗值控制的重要性及控制的關(guān)鍵點(diǎn)。由電抗值計(jì)算公式可以看出，電抗器在頻率、圈數(shù)、鐵芯截面積確定后，鐵心柱的氣隙長(zhǎng)度可以計(jì)算得出。此時(shí)，電抗值的偏差控制取決于氣隙長(zhǎng)度和鐵芯平整度的控制。通過電抗器初步試驗(yàn)，可以確保電抗器制品試驗(yàn)時(shí)電抗值偏差的合格率，進(jìn)一步提高了工效及生產(chǎn)周期。

參考文獻(xiàn)：

[1][美]Colonel Wm.T.Mclyman.變壓器與電感器設(shè)計(jì)手冊(cè)[M].中國(guó)電力出版社，2009.

[2][愛爾蘭]W.G.Hurley，[德]W.H.Wolfle.應(yīng)用于電力電子技術(shù)的變壓器和電感-理論、設(shè)計(jì)與應(yīng)用[M].機(jī)械工業(yè)出版社，2014.

[3]何此昂，周渡海.變壓器與電感器設(shè)計(jì)方法及應(yīng)用實(shí)例[M].人民郵電出版社，2011.

[4]尹克寧.變壓器設(shè)計(jì)原理[M].中國(guó)電力出版社，2003.

[5]路長(zhǎng)柏，朱英浩.電力變壓器計(jì)算[M].黑龍江科學(xué)技術(shù)出版社，1986.