有限覆蓋定理證明實數完備性的其余等價定理
阿力非日,張 艷
(西昌學院彝語言文化學院,四川西昌 615000)
0 引言及預備知識
實數系的完備性是實數的一個重要特征,與之相關的 7個基本定理是彼此等價的,并且是論證其他一些重要定理(如一致連續性定理等 )的依據,它們從不同的方式刻畫了實數集R的一種特性,通常稱為實數的完備性或實數的連續性,因此在理論上具有重要價值.完備性公理等價既是如果把實數分成上、下兩集,當下集里無最大值時,上集必有最小值.這說明實數具有連續性,填滿了整個數軸(沒有空隙).
實數完備性的七個定理:
(1)Heine-Borel有限覆蓋定理:設H為閉區間[a,b]的一個無限開覆蓋,則從H中可選出有限個開區間來覆蓋[a,b]
(2)確界原理:設S為非空數集.若S有上界,則S必有上確界;若S有下界,則S必有下確界.
(3)單調有界定理:在實數系中,有界的單調數列必有極限.
(4)致密性定理:任何有界數列必有收斂的子列.
(5)Cauchy收斂準則:數列{an}收斂的充要條件是:?ε>0,?N∈N*,當n,m>N時有 |an-am|<ε.
(6)區間套定理:若{[an,bn]}是一個區間套,則在實數系中存在唯一的一點ξ,使得ξ∈[an,bn],
n=1,2,…,即anξbn,n=1,2,….
(7)Weierstrass聚點定理:實軸上的任一有界無限點集S至少有一個聚點.
1 具體證明過程
1.1 有限覆蓋定理證明確界定理
證明:反證法.設S為非空數集,設?≠S?R,?x∈S,有xM.?x0∈S.考慮閉區間[x0,M],假如S無上確界,那么?x∈[x0,M]:
(1)當x為S的上界時,必然有更小的上界x1 (2)當x不是S的上界時,自然有更小的上界x2>x.于是x有開鄰域Δx.其中沒點都不是S的上界. 閉區間[x0,M]上每點都可以找出一個鄰域Δx,它要么屬于第一類(每點皆為上界),要么屬于第二類(每點皆不是上界),令H={Δx|x∈[x0,M]},則H是閉區間[x0,M]的一個開覆蓋,根據有限覆蓋定理,必存在有限子覆蓋{Δ1,Δ2,…,Δn},易知M所在的開區間為第一類的,相鄰接的開區間Δx有公共點,也應為第一類的,經過有限次鄰接,可知x0所在的開區間也是第一類的.矛盾. 故S有上確界.證畢. 證明:反證法.不妨設序列{xn}單調遞增,且xnM(n=1,2,…).由{xn}?[x1,M], 假設對?x∈[x1,M],x都不是序列{xn}的極限.則存在ε0>0,對?N∈N*,存在n>N, 有 |xn-x|≥ε0. 故{xn}必存在極限.證畢. 證明:反證法.設{xn}?[m,M]為有界數列,若{xn}中無收斂子列.對?x′∈[m,M],{xn}中無子列收斂于x′,即?x′∈[m,M],?δx′>0,使U(x′,δx′)內只含有{xn}中至多有限項.事實上,若存在x0∈[m,M],對任意δ>0,在U(x0,δ)內都含有{xn}的無窮多項,則{xn}必有子列收斂于x0.令 H={U(x,δx)|x∈[m,M]}. 則H是[m,M]的一個開覆蓋,根據有限覆蓋定理,H中存在有限個鄰域U(x1,δx1),…,U(xn,δxn)使得覆蓋了H,當然也覆蓋了[m,M].由于每個鄰域內只含有{xn}中至多有限項,從而{xn}只有有限項.矛盾. 故{xn}中必含有收斂子列.證畢. 證明:反證法.?ε>0,?N,當m,n>N時,|xm-xn|<ε.取m=N+1,則對?ε>0,當n>N時,有|xn-xN+1|<ε.令ε=1,則當n>N時,有|xn-xN+1|<1,即xN+1-1 故{xn}收斂. 證明:反證法.設{[an,bn]}為閉區間套.但對?x′∈[a1,b1],至少存在k∈N.使得x′?[ak,bk],從而存在δx′>0.使得 U(x′,δx′)∩[ak,bk]=?. 因為G={U(x′,δx′)|x′∈[a,b]}是[a1,b1]的一個開覆蓋,故G中有限個開區間即可完全覆蓋[a1,b1],記為 G*={U(xi,δi)|i=1,2,…,n}. 由此得出 這與G*={U(xi,δi)|i=1,2,…,n}是[a1,b1]的開覆蓋矛盾. 證明:設S是直線上的有界無限點集,于是存在a,b.使得S?[a,b].假定[a,b]中任何一點都不是S的聚點,則對任意x∈[a,b],都存在相應的δx>0,使得U(x,δx)內至多含有S的有限多個點.令 H={U(x,δx)|x∈[a,b]}. 則H是[a,b]的一個開覆蓋,根據有限覆蓋定理,H中存在有限個鄰域U(x1,δx1),…,U(xn,δxn)使得覆蓋了H,當然也覆蓋了S.由于每個鄰域內至多含有S的有限個點,故這n個鄰域的病集也至多只含S的有限個點.于是得到S為有限點集.這與題設S為無限點集矛盾. 因此,在[a,b]中至少有一點是S的聚點.1.2 有限覆蓋定理證明單調有界定理
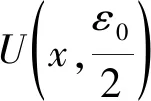
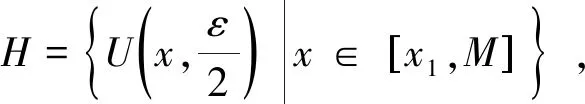
1.3 有限覆蓋定理證明致密性定理
1.4 有限覆蓋定理證明Cauchy收斂準則的充分性
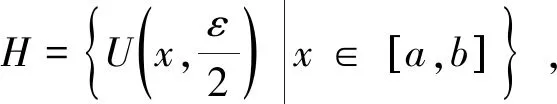
1.5 有限覆蓋定理證明區間套定理
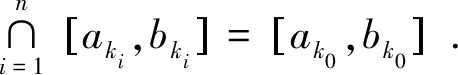
1.6 有限覆蓋定理證明聚點定理


