基于多層神經網絡和PReLU函數的后非線性BSS算法

陳 曦，李 煒，張亞麗，薛青松

(1.安徽工程大學檢測技術與節能裝置安徽省重點實驗室，安徽蕪湖 241000; 2.安徽工程大學電氣工程學院，安徽蕪湖 241000)

0 引言

盲信號處理(Blind Source Separation, BSS)是指在源信號和傳輸信道均未知的情況下，僅僅從觀測信號恢復和提取源信號的一種信號處理方法.近些年，相關課題的研究已經引起了廣泛的關注，并在概率信號的處理、面部識別和醫學圖像處理等領域有了重大突破.BSS信道混疊模型主要包括線性瞬時混疊、線性卷積混疊和非線性混疊.由于非線性模型更能真實地模擬信號傳輸過程，但其理論和傳輸信道較為復雜，不能夠完全分離源信號，所以一般會對非線性模型進行簡化.非線性混迭模型主要有三種：后非線性模型(PNL)、LNL層混疊模型以及Momo非線性混疊模型.從理論上來說，PNL是可能完全分離的，因其結構是最簡單、抗干擾能力最強，且能夠估計出弱信號的排列和平均值.正因如此，現在大部分有關非線性BSS算法的研究主要是針對PNL模型.

Bell等首次提出了以信息最大化準則來建立目標函數的方法，隨后又提出一種基于隨機梯度的最大化熵BSS算法，但是由于隨機梯度的計算量較大而且容易出現局部最優化的解[1].根據這一局限，日本學者Amari提出了穩定、快速的自然梯度算法，該算法的收斂性和穩定性優于其它的算法；傳統的自然梯度算法都是選擇單一步長，但其不能很好的平衡收斂速度與系統穩定性[2-3].季策等人提出了將自然梯度算法用來解決在非平穩條件下的瞬時盲信號處理難題，首先利用系統上的波動對代價函數進行自適應約束并加以調整，同時引入變步長來控制自然梯度算法，使其更具穩定性，此算法可以解決分離過程中嚴重的穩態誤差[4].歐世峰等人在解混矩陣的公式中添加動量項，通過控制滑動參數和動量因子來選取最優步長，結合了兩個參數的優勢，進一步平衡了收斂速度和穩定性的關系，以此分離混合信號，該方法優化了收斂速度與穩定性之間的關系，但由于該算法需要兩個參數同時控制，所以會使算法變得復雜[5]；馬志陽等人通過構造非線性單調函數，使得步長與動量因子可以自適應調節，從而可以在平衡收斂速度和穩定性的條件下選擇參數，該算法可以有效地緩解固定值對算法性能的約束，并且在噪聲環境下同樣有較好的分離效果[6].趙峰等人以tanh函數作為多層神經網絡的激活函數，并通過其來估計任意的概率密度函數，從而給出信號的代價函數，該算法不需要源信號的任何先驗條件、收斂速度快且可以用非線性函數代替代價函數，但是容易造成梯度消失[7].

本文針對后非線性盲源分離問題提出了一種基于多層神經網絡的分離算法，該方法選用PReLU函數作為多層神經網絡的激活函數，進而對概率密度函數進行自適應估計，利用最小互信息準則構建目標函數，并通過優化后的自然梯度算法對目標函數進行迭代尋優.

1 后非線性混合-解混系統

后非線性混合-解混系統如圖1所示，左邊是混合系統，右邊為解混系統.首先，將源信號通過混合矩陣An×n進行線性混合，得到中間變量V(t)=[v1(t),···,vN(t)]T，其表達式為：

V(t)=AS(t)

(1-1)

圖1 后非線性混合-解混系統Fig.1 Post Nonlinear Mixing-Demixing System

將V(t)通過含待測參數的線性函數f(·):RN→RN進行線性混合，求得映射非線性混疊函數的逆f(·)之后，通過奇異線性分離矩陣Wn×n，得出Y(t),再選擇恰當的目標函數來測試信號之間的獨立性，以此來判斷輸出信號矢量是否滿足信號源的統計獨立要求.

令其混合模型如下：

X(t)=f(A×S(t))+N(t)

(1-2)

令S(t)=[s1(t),···,sN(t)]T為N路統計獨立源向量，X(t)=[x1(t),···,xN(t)]T為觀察得到的N路的混合信號N(t)=[n1(t),···,nN(t)]T，為N維加性高斯白噪聲，并且高斯白噪聲與信號源的互相關性為0；f(·)為可逆可導的未知非線性函數，W為非奇異正定矩陣，且一般不考慮噪聲對模型的影響，則觀測信號可以表示為：

(1-3)

其中，aij為正定混合矩陣的標量項.

則非線性的解混模型如下：

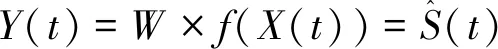
(1-4)

2 構建目標函數

2.1 目標函數的選取

若任意一組的聯合概率密度函數都可以地分解為qj，其為第jth個源信號的概率密度函數，則這一組信號是獨立的.最小化互信息(MMI)的基本思路是：求解混迭矩陣W，使輸出Y(t)的各分量之間的互相關性達到最小.

令yi為估計的各個源信號向量，pi(yi)為各個分量的概率密度函數，首先選擇一個完全的獨立概率密度分布q(y)=∏iqi(yi)，并考慮概率密度函數pi(yi)和q(y)之間的KL散度：

(2-1)

其中，py(y)為分離信號y的聯合概率密度函數，KL離散度為非負的，當且僅當p=q時，KL散度可以達到它的最小值，并且它與香農互信息是等價的.

(2-2)

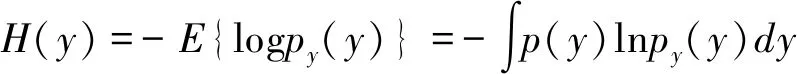
在非線性函數條件下的KL散度可以表示為：

KL(p(y)||q(x))=KL[p(f(y))||q(f(x))]

(2-3)

由上式可知，任意可逆的非線性函數都不影響源信號之間的非高斯性，如Z=h(y)=f(x)表示可微映射，則該映射的輸入和輸出聯合分布之間的關系如下：

(2-4)

其中，|J|是變換的雅各布矩陣的行列式.

聯合微分熵關于分離矩陣W的表達式為：

(2-5)

使用自然梯度法對熵函數H(Z)求導并得到它的最大化：

(2-6)

由于輸出的邊際概率密度函數p(y)決定了邊際熵，且概率密度函數是變換的，所以將互信息最小化問題轉化成概率密度函數與模型參數的最小比值問題.

得出自然梯度迭代法的表達式：

(2-7)

2.2 非線性函數的選取

自然梯度算法的收斂性能和穩定性能取決于步長因子ηt和非線性函數的選擇.在盲源分離算法中，對于統計特性未知的信號源來說，若不知源信號的先驗分布，僅僅根據經驗或是某種信號的統計特性來選擇非線性函數的話，會使得源信號的分離不夠準確.

所以本文選擇以PReLU函數為多層神經網絡的非線性函數，有效解決了Sigmoid函數的均值偏移和梯度消失的缺陷，當x≥0時，導數f'(x)=0，所以PReLU函數能夠在x≥0時，不會造成梯度消失的問題，并且該函數具有非飽和性，所以能夠有效解決均值偏移和神經元在負區間死亡的問題，表達式如下：

(2-8)

其中，i表示不同的通道.

(2-9)

令輸入信號的概率密度函數為p(x)時，假如H(x,w)近似為F(x)，則神經網絡的輸出服從max(0,x)均勻分布，得到：

(2-10)

令yim,m=1,2,...,M,Zim,m=1,2,...,M分別為神經網絡的輸入與輸出.

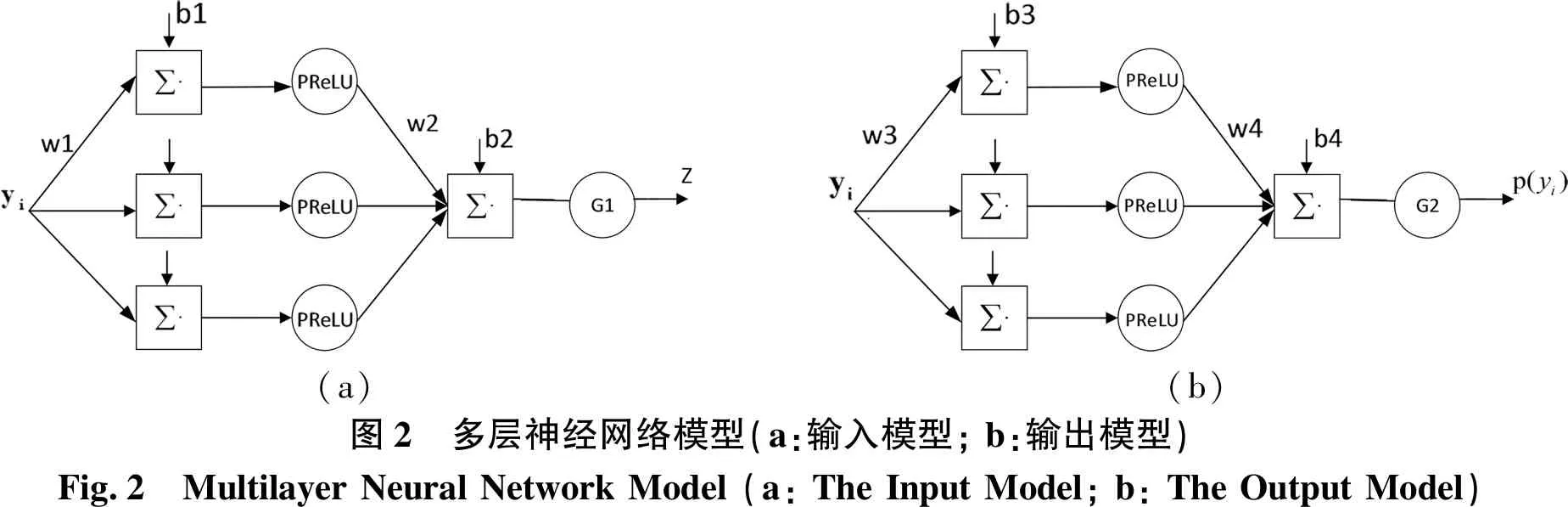
(a)(b)圖2 多層神經網絡模型(a:輸入模型; b:輸出模型)Fig.2 Multilayer Neural Network Model (a: The Input Model; b: The Output Model)

如圖2所示，構建一個單隱層神經網絡，其包含3個神經元，其中單隱層神經元激活函數PReLU(·)，當神經網絡迭代收斂時，則：

(2-11)

令yi的概率密度函數的表達式為：

(2-12)

在非線性模型中，直接對p(yi)求導或是微分得出一階導數p'(yi)，可能會導致精度不搞，但是多層神經網絡能夠較好的逼近非線性函數，可以使得p'(y)估計更加準確.

(2-13)

得出：

(2-14)

3 基于神經網絡的概率密度估計算法

為了使每個信源被提取出來都是獨立分布的，所以對wi(0)每次都賦給不同的數，以保證每次從混合信號里面取出的源信號是不同的.首先對矩陣W進行正交化和白化處理，過程如下：

(1)將有關信號源的數據零均值和中心化處理，使得它的均值等于0；

(2)對數據進行白化處理:x→z；

(3)用多層神經網絡去估計Z的概率密度函數p(z)；

(4)設M個待提取的獨立分量，從1開始計數；

(5)給wi(0)賦初始值，計算2-范數，并規定||wi(0)||2=1；

(6)將p(z)和wi(k)代入式中即可得到y的概率密度函數p(y)，使得f(y)=p(y)；

(7)將式wi(t+1)=ηt{I-φ(y(t))yT(t)}wi(t)進行迭代；

(8)將得到的W進行正交歸一化處理；

(9)加入wi未收斂，則回到步驟(5)；

(10)令C=C+1，判斷C是否大于M，如果是，則算法結束，如果不是，則算法轉回步驟(4).

本文所有仿真實驗皆在Matlab里面完成，利用自然梯度算法和改進后的基于多層神經網絡的自然梯度算法分別對混合信號進行分離，并得出仿真圖.本文選取了4種源信號，包含了亞高斯信號和超高斯信號，原始信號如下所示：

(3-1)

在(3-1)式中，s1信號是符號信號，s2信號是高頻正選信號，s3信號是低頻正弦信號，s4信號是調幅信號.本文選用了100個采樣點，如圖3至圖6所示，橫坐標代表了采樣區間，縱坐標代表了幅度.本文將傳統和改進之后自然梯度算法分離所得的信號波形與源信號波形作對比，來驗證算法的可行性.

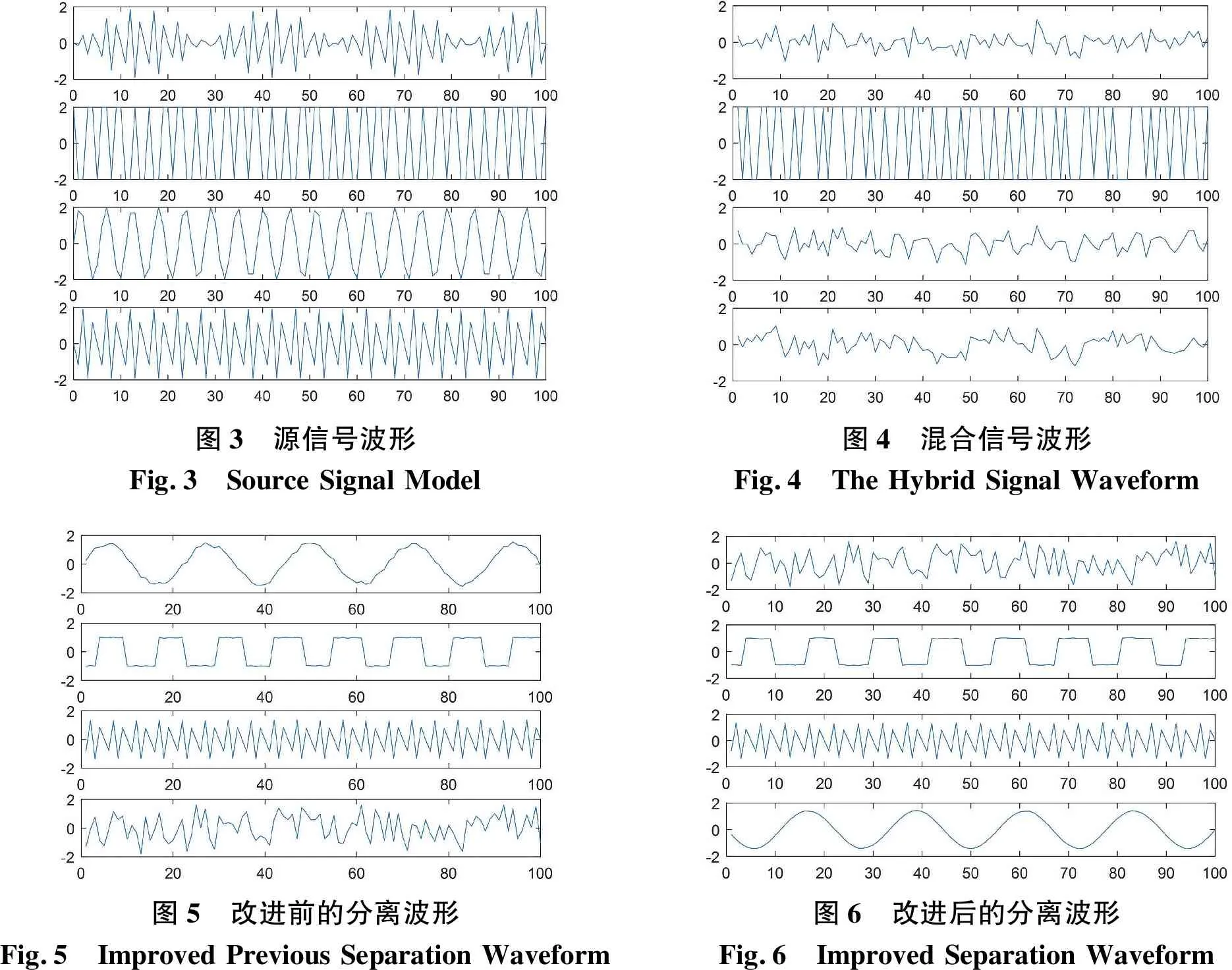
圖3 源信號波形Fig.3 Source Signal Model圖4 混合信號波形Fig.4 The Hybrid Signal Waveform圖5 改進前的分離波形Fig.5 Improved Previous Separation Waveform圖6 改進后的分離波形Fig.6 Improved Separation Waveform

由圖5、圖6可以看出，以PReLU函數作為多層神經網絡的激活函數，可以更好地將源信號分離出來.由于盲源分離具有隨機性，即與源信號相比，無論是幅度和順序皆有差異，所以僅從波形是無法準確判斷這兩種算法的好壞.因此，本文采用了性能指標PI來對算法的分離效果進行評價，以此來分析分離信號與原始信號的相似度.PI曲線越接近橫坐標，則相似度越高；當PI=0時，則分離信號與原始信號的波形完全吻合.PI參數定義如下：

(3-2)

在(3-2)式中，B為分離矩陣，則可以得到全局矩陣G=BA，gij為全局矩陣G里的元素，maxi|gij|是G的第i行元素的最大值，maxj|gji|是第i列元素的最小值.

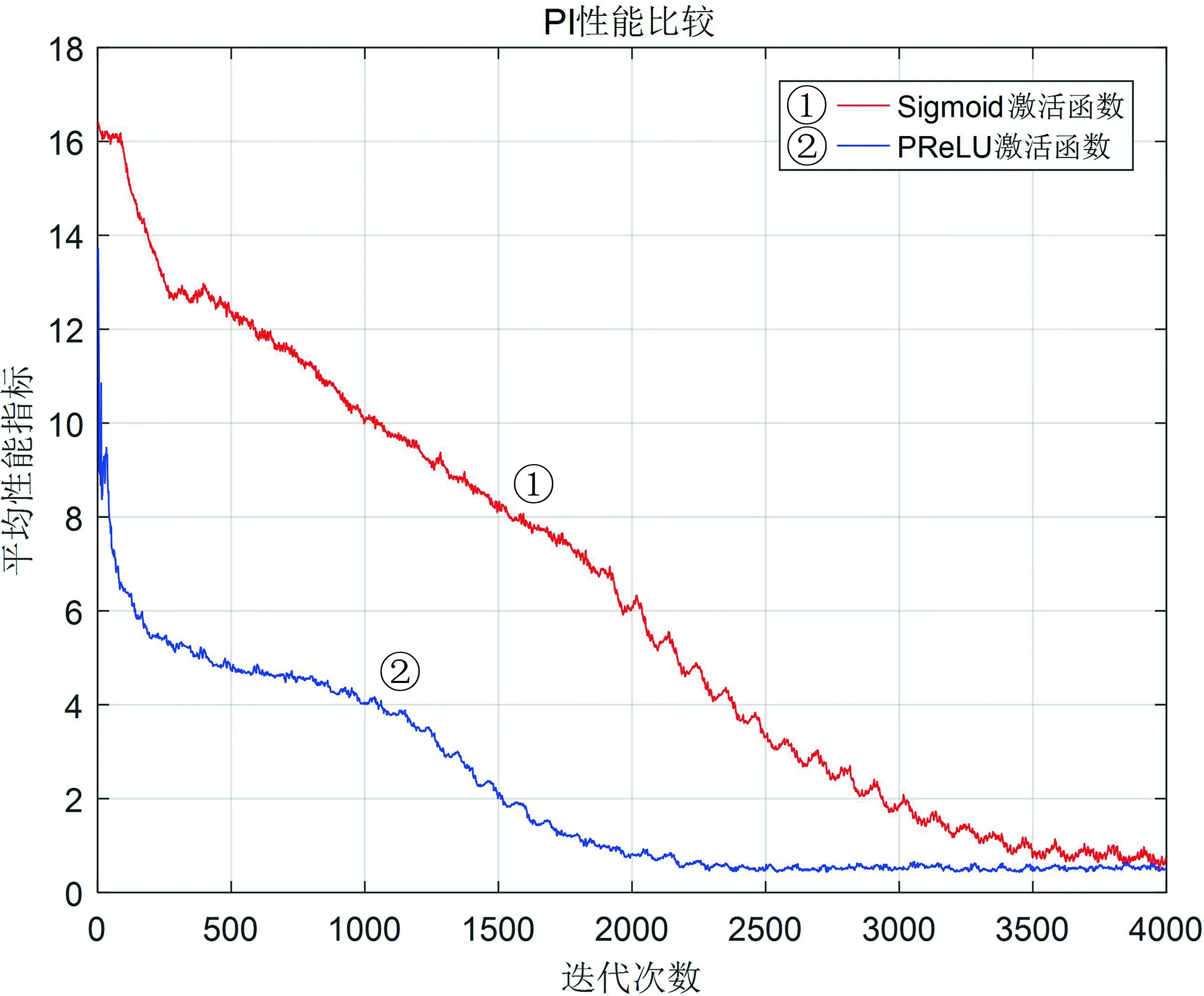
圖7 PI性能比較圖Fig.7 PI Performance Comparison Diagram

為了比較傳統算法與改進算法的分離效率，在相同的環境下，對同一種混合信號進行分離，比較兩種算法的收斂速度與穩定性能.如圖7所示，改進后的自然梯度算法在收斂速度上比傳統的自然梯度算法有明顯提高，而且在其趨于平穩階段，波動性更小，所以穩態誤差也相對較小；傳統的自然梯度算法在3 500步左右時開始逐步趨于穩定，而改進之后的算法在2 000步左右時也才開始趨于穩定；并且改進之后的算法PI值在0.908附近波動，而傳統的自然梯度算法則在1.509的附近波動.綜上所示，改進之后的算法在分離混合信號時的收斂曲線更光滑且振幅更小，有效地提升了算法的整體性能，使得信號的分離效果更好.

4 結論

本文提出了一種以PReLU函數為激活函數，并通過多層神經網絡來估計任意信號的概率密度函數的后非線性盲源分離算法，該算法是在傳統的MMI算法的基礎上改進而來，可以有效解決在激活函數在負區間梯度消失的缺陷，仿真實驗證明在分離信號的收斂速度和穩定性能上有顯著的提高.但本文所研究的后非線性模型的發展并不成熟，源信號是需要知道它的先驗分布，并且真實環境中是無法避免的，所以應對這一問題做進一步的研究.