基于預測方法的郵輪定價方案

閆述濤，李凱，康彤

(中國傳媒大學理工學部，北京100024)

1 引言

近年來乘坐郵輪旅游的人越來越多，郵輪公司的發展也非常迅速。郵輪采用提前預訂的方式進行售票，郵輪出發前0周至14周為有效預定周期，郵輪公司為了獲得每次航行的預期售票收益，希望通過歷史數據預測每次航行0周至14周的預定艙位人數、預訂艙位的價格，為保證價格的平穩性，需要限定同一航次相鄰兩周之間價格浮動比，意愿預定人數轉化為實際預定人數與定價方案密切相關。我們通過假設某郵輪公司擁有一艘1200個艙位的郵輪，艙位分為三種，250個頭等艙位，450個二等艙位，500個三等艙位。

該郵輪每周往返一次，同一航次相鄰兩周之間價格浮動比不超過20%。我們采用三種不同的預測方法預測每次航行各周預訂艙位的人數，完善各航次每周實際預訂人數非完全累積表，并分析結果。

2 模型的建立與求解

在已知前4個航次每周實際預訂人數非完全累積表的基礎上要求我們對后面6個航次的預訂人數進行預測。首先要對任意兩周之內數據利用spss進行線性相關性分析，然后選定一元線性回歸分析法，加法增量法，乘法增量法通過建立數學模型，預測某一周內某個時間點的各個航次實際預訂人數。

2.1 一元線性回歸分析

1)一元線性回歸分析法是對客觀事物數量關系的分析，是一種重要的統計分析方法，被廣泛的應用于社會經濟現象變量之間的影響因素和關聯的研究。回歸分析的主要目的是要通過樣本回歸函數(模型)SRF盡可能準確的估計總體回歸函數(模型)SRF。估計方法有很多種，我們使用最小二乘法來估計回歸系數。

2)選取數據，定義變量

本文選取了各航次每周實際預定人數非完全累積表中同等艙次第i周的數據設為 X；第i-1周的數據設為Y。選取二等艙次第12周與第11周的樣本數據，如表1所示：

表1

根據以上數據，利用spss對上述 X 和Y 進行相關性分析，圖1是 X 和Y 散點圖，圖2為相關性分析結果。

圖1

圖2

從圖1和圖2可以得出，二等艙次第12周與第11周實際預定人數之間有較明顯的線性相關關系，同樣可以得出同等艙次第i周與第i-1周之間也有明顯的線性關系。因此，同等艙次第i周與第i-1周兩個變量之間是一元線性回歸關系。

3)建立模型

設一元線性樣本回歸模型為：

(1)

計算公式：

(2)

由上式可以計算出回歸系數：a=15.0873；b=0.8086

可以確定回歸方程為：F=15.0873+0.8086X

4)求解結果如表2。

2.2 加法增量法

1)加法增量發法是基于增量數據矩陣預測某一時間點到啟航這一時間內將要到達的總需求。于是，我們在已知前四個航次完整的每周實際預訂人數情況下利用加法增量法預測某一航次與時間點的未知預訂人數。

表2

2)建立數學模型

加法增量法僅考慮已經啟航航次的歷史數據，即航次1到航次n的數據。此時，航次m的總人數預測為：

(3)

1-5航次的頭等艙數據矩陣如表3所示：

表3

3)模型求解

由表三中所給數據求第5航次第0周頭等艙的預訂人數。首先求前4個航次頭等艙第1周與第0周的數據增量和，即：

(171-170)+(184-184)+(213-210)+(212-210)=6

再求平均增量，即6/4=1.5；最后求第5次航行頭等艙的預定人數，即200+1.5=201.5，最后對得出的人數進行取整，即第5航次第0周頭等艙的預訂人數201。通過MATLAB對加法增量法進行編程，輸入相應的數據，預測指定時間點和指定航次的預訂人數，完善附件中各航次每周實際預訂人數非完全累積表如表4。

2.3 乘法增量法

1)乘法增量法是基于需求增加的百分比(增量百分比)來預測未來需求或者需求的增量法。根據附件中表格所給數據，我們通過乘法增量法預測某一航次與時間點的未知預訂人數。

2)模型建立

增量百分比是指在一定時間段內新增加的需求占以前總預訂量的百分數，即：

表4

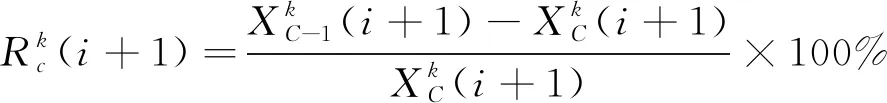
(4)

此時，航次m的總需求預測可以通過以下的方法得到：

(5)

(6)

1-5航次的頭等艙數據矩陣如表5所示

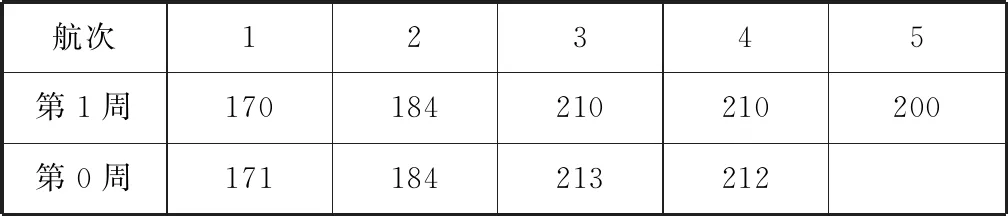
表5

3)模型求解

由表三中所給數據求第5航次第0周頭等艙的預訂人數。首先求出前4次航行的第0周和第1周的增量百分比：

再計算增量200×2.97%=5.94，最后預測出第0周第5次航行的預定人數為200+6=206人。同樣的可以通過MATLAB編程軟件編程，輸入數據對其它某航次某時間點的預訂人數進行預測。

求解結果以表格形式給出，如表6。

3 三種預測模型的結果分析與比較

通過MATLAB作出三種方法預測的預訂人數與實際預訂人數的圖像從圖2可以看出加法增量法預測出的預訂人數與實際預訂人數的曲線最吻合，而且通過離差分析法計算出的數據可以看出加法增量法預測出的誤差最小。如表7和圖3。

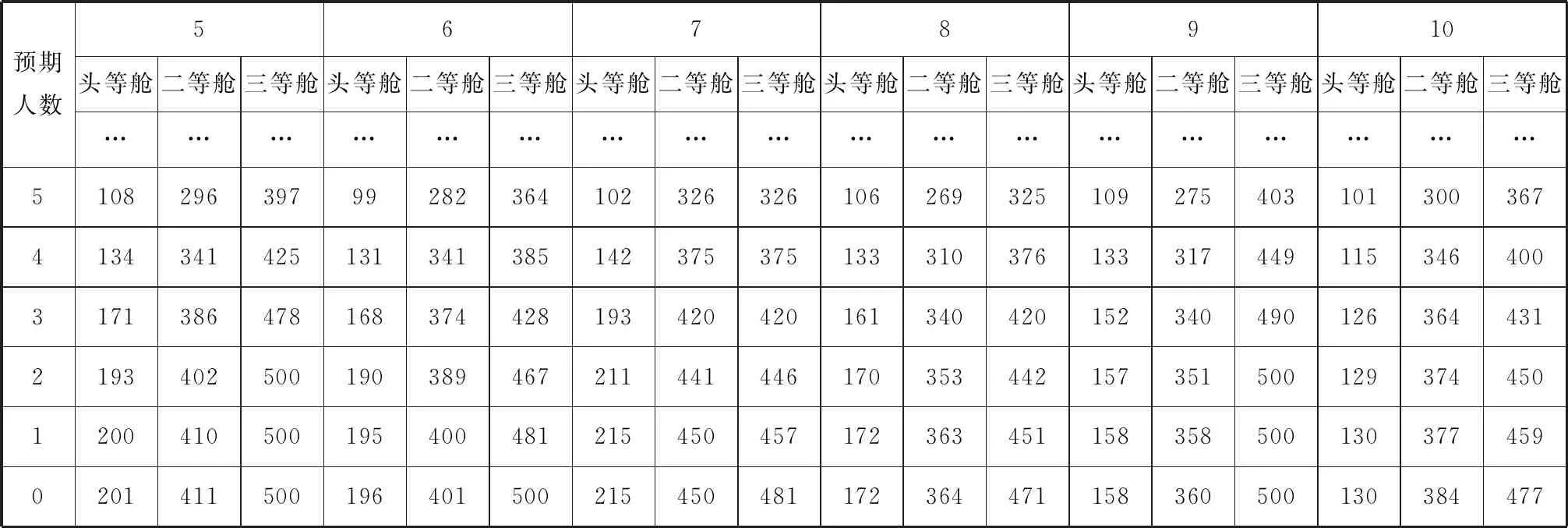
表6

表7

圖3

通過以上表格與圖3可以看出加法增量法預測出的人數與實際人數相比誤差最小，得出結論，在以上三種方法中，加法增量法預測最優。

4 結論

本文以一艘有1200個艙位的游輪的預訂艙位人數，預訂艙位價格為研究對象，采用預測的方法，分析了各研究對象的特性，完善了表格。另外，建立了郵輪每次航行的最大預期售票收益模型，有利于提高公司的預期售票收益。