復合函數含參問題研究

安徽省寧國中學 陳曉明 242399

近年來，復合函數含參問題時常悄然出現在高考及各級各類模考的舞臺．由于復合函數的多樣性及含參問題的復雜性，對學生的思維能力、邏輯推理能力、運算能力等要求較高，對學生的數學基礎知識掌握是否扎實、數學思想方法是否能靈活運用都是一個考驗.學生普遍害怕此類試題，在考場上經常選擇放棄.因此，本文通過實例對此類問題進行研究，以求提供解決此類問題的一些策略和方法．

A.1 B.2 C.3 D.4

分析：這里要判斷函數零點的個數與實數a的存在性的關系，遇到函數零點的問題我們通常轉化為對應方程的根的問題，進一步轉化為兩個函數圖像的交點問題．這里問題的難點在于函數g(x)是一個復合函數，令g(x)=h(f(x))，它的零點的個數即方程h(f(x))=0的異根的個數．令內層函數t=f(x)，則外層函數為y=h(t)，特別應該引起注意的是內層函數t=f(x)的值域是外層函數y=h(t)的定義域．因此解決此類問題通常要分別畫出內層函數和外層函數的圖像，然后根據兩個函數圖像、結合函數性質、利用數形結合的思想來進行思考．

解：因為x≥0時，f(x)=4x3-6x2+1，所以f′(x)=12x2-12x=12x(x-1)，故函數在[0,1]上單調遞減，在[1,+∞)上單調遞增；另外，x＜0時，f(x)=ex∈(0,1)，所以內層函數t=f(x)的最小值為f(1)=4-6+1=-1．其圖像如圖1所示，函數t=f(x)的最低點為A(1,-1)，函數的值域為[ - 1,+∞)，即外層函數y=h(t)的定義域為[-1,+∞).令y=h(t)=t2-t+a=0，則t2-t=-a，t∈[ - 1,+∞),方程t2-t=-a，t∈[-1,+∞)根的個數即函數y=t2-t，t∈[-1,+∞)與常數函數y=-a圖像的交點個數.如圖2所示，函數y=t2-t，t∈[-1,+∞)圖像最低點為B

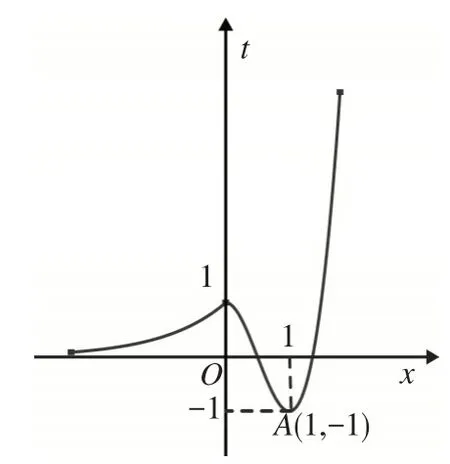
圖 1

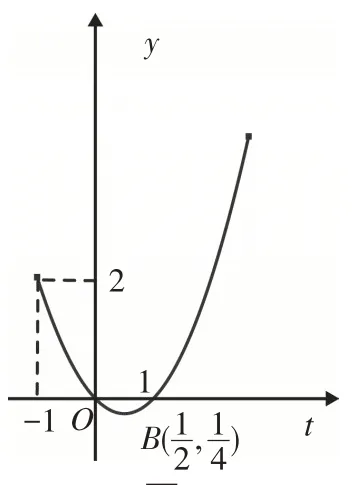
圖2

對于命題1：取-a=-1，即a=1，易知函數y=t2-t，t∈[-1,+∞)與y=-1圖像無交點，如圖3所示，故方程t2-t=-a無解，進一步可知方程無解，即存在實數a使得函數g(x)沒有零點，所以命題1成立．

對于命題2：取-a=2，即a=-2，則由方程t2-t=2解得t1=-1,t2=2，如圖4所示．當t=-1時，由上述解法可知x=1；當t=2時，由圖像可知對應唯一的自變量x0，如圖5所示，因此存在實數a使得函數g(x)有2個零點，所以命題2成立．

圖3

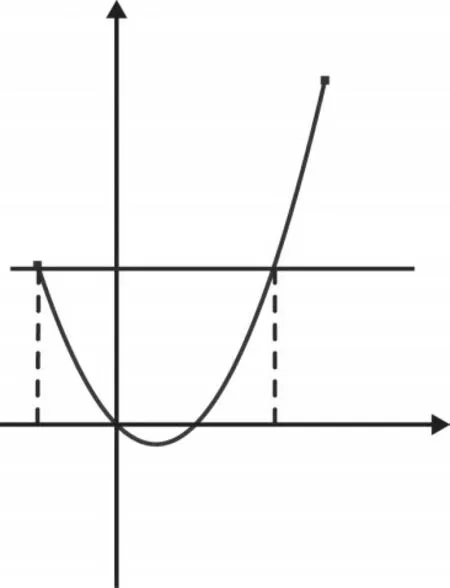
圖4

對于命題3：取-a=0，即a=0，則由方程t2-t=0解得t1=0,t2=1，如圖2所示．當t=0時，由圖1可知對應兩個自變量0＜x1＜1,x2＞1；當t=1時，由圖1可知對應兩個自變量x3=0,x4＞1，因此存在實數a使得函數g(x)有4個零點，所以命題3成立．

圖5

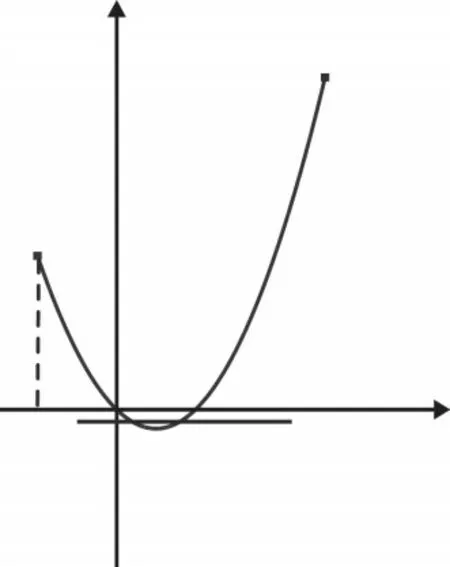
圖6

因此，本題正確答案是D．

點評：由上述解法可知，判斷復合函數g(x)=h(f(x))零點的存在性，首先要“換元解套”（這里令內層函數t=f(x)，則外層函數為y=h(t)），然后由參數a的值，判斷外層函數y=h(t)零點個數及零點的大小（這里通過判斷函數y=t2-t，t∈[-1,+∞)與常數函數y=-a圖像的交點橫坐標來確定），再由該零點的大小（即t的值）及個數通過內層函數t=f(x)的圖像來確定復合函數g(x)=h(f(x))的零點的個數.這里滲透了化復雜為簡單，化未知為已知，化陌生為熟悉的轉化與化歸的思想方法，另外還滲透了函數與方程、數形結合、分類討論等思想方法．

變式 條件不變，問函數g(x)零點的個數可能為哪些值？對應的實數a的范圍是什么？

解析：由上述函數圖像及解析不難判斷有 下 列 結 論：（1），函數g(x)沒有零點；（2）當時（此時對應，函數g(x)有3個零點；（3）當時（此時對應t有兩個值t1,t2，且，每個t值對應3個零點），函數g(x)有6個零點；（4）當-a=0，即a=0時（見上述解法中對于命題3的分析），函數g(x)有4個零點；（5）當-a∈( 0 ,2)，即a∈( - 2,0)時（此時對應t有兩個值t1,t2，且-1＜t1＜0，t2＞1，兩個值t1,t2分別對應2，1個零點），函數g(x)有3個零點；（6）當-a=2，即a=-2時（見上述解法中對于命題2的分析），函數g(x)有3個零點；（7）當-a∈( 2 ,+∞)，即a∈( - ∞,-2)時（此時對應唯一的t值，且t＞1，該t值對應1個零點），函數g(x)有1個零點．

A.2 B.3 C.5 D.8

分析：本例中若令g(x)=h(f(x))=f2(x)+af(x)-b2，則它與例1相同的是都是一個二次函數（外層函數y=h(t)）與分段函數（內層函數t=f(x)）的復合函數；不同的是提供條件及求解問題有所不同，當然這里求實數a的最大值可以首先確定實數a的取值范圍.由y=h(t)=t2+at-b2＜0可求出t的范圍（含參），再由t的范圍，結合內層函數t=f(x)的圖像和性質，以“不等式恰有1個整數解”為突破口，確定參數b的值，再進一步由t的范圍（需對參數a進行分類討論）確定這1個整數解的值，從而求得自變量x的范圍，再得到參數a的具體范圍．

解：令t=f(x)，則y=h(t)=t2+at-b2＜0,當b≠0時，因為根的判別式Δ=a2+4b2＞0,所以由韋達定理得對應方程兩根之積t1t2=-b2＜0，如圖7所示，易知不等式的解集為( t1,t2).顯然0∈(t1,t2)，當t=f(x)=0時，由內層函數t=f(x)的圖像可知方程有兩個整數解0,2，如圖8所示，這與“不等式恰有1個整數解”不符，故b=0．

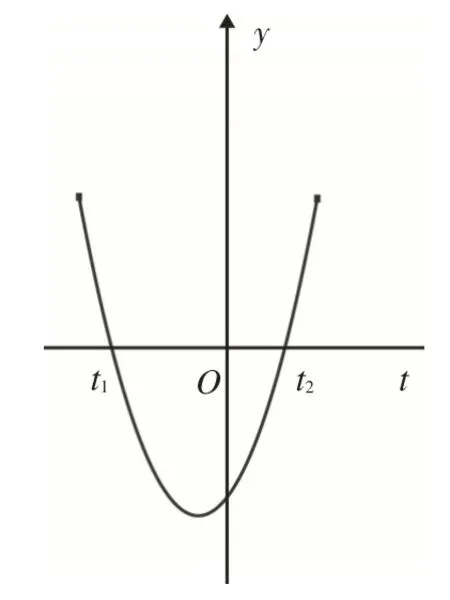
圖7

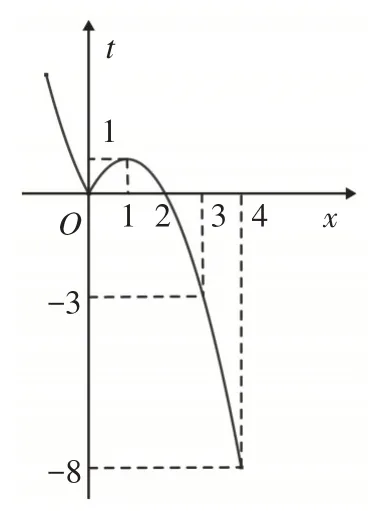
圖8

這樣不等式可化為y=h(t)=t2+at＜0.（1）當a＜0時，不等式y(tǒng)=h(t)=t2+at＜0解集為(0,-a).①當0＜-a＜1，即-1＜a＜0時，如圖9所示，不等式0＜f(x)＜-a解集為(x1,0)?( 0 ,x2)?(x3,2)，顯然其中無整數解，與題意不符，故這種情況不成立；②當-a=1，即a=-1時，不等式0＜f(x)＜1解集為(x1,0)?(0,1)?(1,2)（其中-1＜x1＜0，因為f( - 1)=3），顯然其中也無整數解，與題數與方程、數形結合、分類討論等思想方法．

變式 條件不變，問函數g(x)零點的個數可能為哪些值？對應的實數a的范圍是什么？

解析：由上述函數圖像及解析不難判斷有 下 列 結 論：（1），函數g(x)沒有零點；（2）當時（此時對應，函數g(x)有3個零點；（3）當時（此時對應t有兩個值t1,t2，且，每個t值對應3個零點），函數g(x)有6個零點；（4）當-a=0，即a=0時（見上述解法中對于命題3的分析），函數g(x)有4個零點；（5）當-a∈( 0 ,2)，即a∈( - 2,0)時（此時對應t有兩個值t1,t2，且-1＜t1＜0，t2＞1，兩個值t1,t2分別對應2，1個零點），函數g(x)有3個零點；（6）當-a=2，即a=-2時（見上述解法中對于命題2的分析），函數g(x)有3個零點；（7）當-a∈( 2 ,+∞)，即a∈( - ∞,-2)時（此時對應唯一的t值，且t＞1，該t值對應1個零點），函數g(x)有1個零點．

A.2 B.3 C.5 D.8

分析：本例中若令g(x)=h(f(x))=f2(x)+af(x)-b2，則它與例1相同的是都是一個二次函數（外層函數y=h(t)）與分段函數（內層函數t=f(x)）的復合函數；不同的是提供條件及求解問題有所不同，當然這里求實數a的最大值可以首先確定實數a的取值范圍.由y=h(t)=t2+at-b2＜0可求出t的范圍（含參），再由t的范圍，結合內層函數t=f(x)的圖像和性質，以“不等式恰有1個整數解”為突破口，確定參數b的值，再進一步由t的范圍（需對參數a進行分類討論）確定這1個整數解的值，從而求得自變量x的范圍，再得到參數a的具體范圍．

解：令t=f(x)，則y=h(t)=t2+at-b2＜0,當b≠0時，因為根的判別式Δ=a2+4b2＞0,所以由韋達定理得對應方程兩根之積t1t2=-b2＜0，如圖7所示，易知不等式的解集為( t1,t2).顯然0∈(t1,t2)，當t=f(x)=0時，由內層函數t=f(x)的圖像可知方程有兩個整數解0,2，如圖8所示，這與“不等式恰有1個整數解”不符，故b=0．

圖7

圖8

這樣不等式可化為y=h(t)=t2+at＜0.（1）當a＜0時，不等式y(tǒng)=h(t)=t2+at＜0解集為(0,-a).①當0＜-a＜1，即-1＜a＜0時，如圖9所示，不等式0＜f(x)＜-a解集為(x1,0)?( 0 ,x2)?(x3,2)，顯然其中無整數解，與題意不符，故這種情況不成立；②當-a=1，即a=-1時，不等式0＜f(x)＜1解集為(x1,0)?(0,1)?(1,2)（其中-1＜x1＜0，因為f( - 1)=3），顯然其中也無整數解，與題意不符，故這種情況不成立；③當1＜-a≤3，即-3≤a＜-1時，如圖10所示，不等式0＜f(x)＜-a解集為(x1,0)?(0,2)（其中x1為直線y=-a與函數t=f(x)圖像交點橫坐標，且-1＜x1＜0，f( - 1)=3），該解集中有唯一整數解1，符合題意，但此時實數a無最大值.④當-a＞3，即a＜-3時，不等式0＜f(x)＜-a解集為(x1,0)?(0,2)（其中x1為直線y=-a與函數t=f(x)圖像交點橫坐標，且x1＜-1，f( - 1)=3），該解集中整數解的個數至少為2個（-1和1），與題意不符，故這種情況不成立．

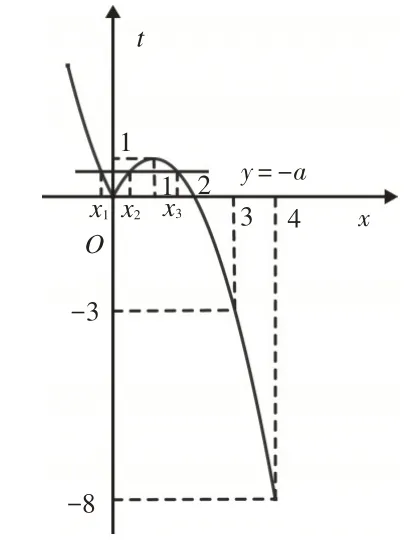
圖9

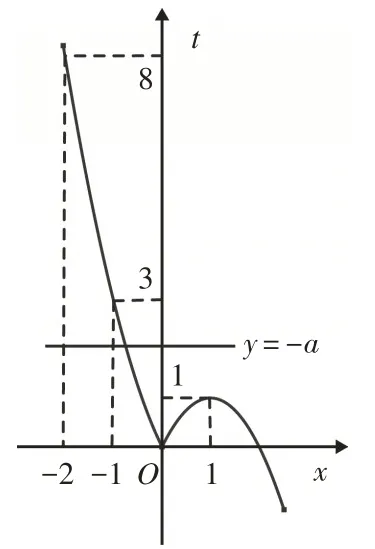
圖10

（2）當a=0時，不等式y(tǒng)=h(t)=t2＜0，解集為空集，故這種情況不成立．

（3）當a＞0時，不等式y(tǒng)=h(t)=t2+at＜0解集為( - a,0)，如圖9所示，不等式-a＜f(x)＜0解集中“恰有1個整數解”必定為3.因為f(3)=-3，f(4)=-8，所以-8≤-a＜-3，即3＜a≤8，所以實數a的最大值是8．

由（1），（2），（3）知，實數a的最大值是8，故本題正確答案是D.

A.b＜0且c＞0 B.b＞0且c＜0

C.b＜0且c=0 D.b≥0且c=0

解：如圖11所示，只要方程f2(x)+bf(x)+c=0中能解出f(x)的兩個值，其中一個值等于0（可得c=0）,另一個值大于0（f2(x)+bf(x)=0可 得 f(x)=-b＞0）,故本題正確答案是C．

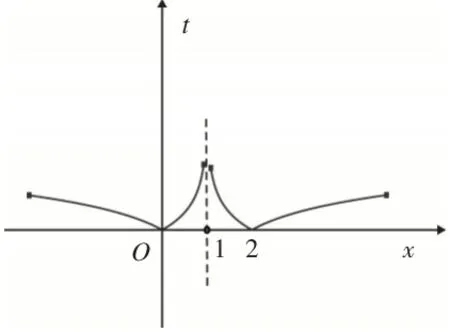
圖11

點評：此解法其實使用了換元法的思想，得出方程f2(x)+bf(x)+c=0有7個不同實數解的充要條件是關于t的二次方程t2+bt+c=0有兩個不等的實根，其中一根為0（可得c=0），另一根為正數（t2+bt=0，可得b=-t＜0）．這樣就自然地將復雜問題化為我們熟悉的簡單問題．

規(guī)律總結

由上述實例我們不難看出，復合函數含參問題通常與不等式、方程聯系在一起，通常其中一個是分段函數，通過提供的條件（如函數零點個數、不等式解集中的特殊解、方程根的個數等），求參數的取值范圍（包括最值）．解決這類問題的關鍵是首先對復合函數g(x)=h(f(x))“換元解套”（這里令內層函數t=f(x)，則外層函數為y=h(t)），然后結合兩個函數的圖像及性質解決問題．特別引起注意的是內層函數t=f(x)的值域是外層函數y=h(t)的定義域.