立體幾何中的動點軌跡問題

福建省南安國光中學 黃清波 362321

立體幾何中的動點軌跡問題是較為新穎的一種創新命題形式，它重點體現了在解析幾何與立體幾何的知識交匯處設計圖形.不但考查了立體幾何點、線、面之間的位置關系，而且又能巧妙地考查求軌跡的基本方法，是表現最為活躍的一種創新題型.這類題型因涉及動點的軌跡問題從而使得要解決的問題處于動態變化之中，需要學生有敏捷的數學觀察力和熟練的轉化能力，技巧性強且難以操控，對學生知識以及思維能力要求較高.本文以福建省泉州市2020屆普通中學高中畢業班質量檢查理科卷第12題為例,對這類問題的解法進行剖析，希望對大家有所幫助.

題目：直四棱柱ABCD-A1B1C1D1中，底面ABCD是邊長為4的正方形，AA1=23．點M是側面BCC1B1內的動點（不含邊界），AM⊥MC，則A1M與平面BCC1B1所成角的正切值的取值范圍為．

命題意圖：本題涉及到動點的軌跡問題，表面上是求線面角，實際是轉化為考查空間圖形的截面軌跡問題，考查了化歸與轉化的思想，考查直觀想象、邏輯推理和數學運算核心素養，體現基礎性與創新性，有一定難度,本次質檢得分率極低.

策略一：降維法

思路分析：根據題意，畫出圖形，對于平面BCC1B1來說，AM是斜線，點M是斜足，AB是垂線，點B是垂足，所以BM是射影，因為AM⊥MC,得到MC⊥BM，所以點M在平面BCC1B1內的軌跡是以BC為直徑的半圓（不包含B,C點）.因為A1B1⊥平面BCC1B1,所以∠A1MB1為A1M與平面BCC1B1所成角.結合B1M的取值范圍，即可得正切值的取值范圍.

解法1:如圖1，已知四棱柱ABCDA1B1C1D1是正四棱柱，所以AB⊥平面BCC1B1.又MC?平面BCC1B1,所以AB⊥MC.因為AM⊥MC，AB?AM=M,所以MC⊥平面ABM.又BM?平面ABM，所以MC⊥BM.因為點M是動點，點B,C是定點，所以在平面BCC1B1內點M的軌跡是以BC為直徑的半圓（不包含B,C點）.因為A1B1⊥平面BCC1B1，所以∠A1MB1為A1M與平面BCC1B1所成角.在RT△A1MB1中，.取BC的中點N，由已知得又A1B1=4，所以tan∠A1MB1的取值范圍為

圖1

歸納：降維法，即空間問題平面化法，利用立體幾何的相關知識把空間的幾何量關系、位置關系等轉化到同一平面內，空間問題平面化，然后結合解析幾何中有關軌跡定義（如圓、橢圓、雙曲線、拋物線、線段垂直平分線、角平分線等），求出對應的軌跡.常用的方法有：平移法、射影法、展開法、輔助面法等.

變式：如圖2，在正方體ABCD-A1B1C1D1中，點P為BCC1B1面內一動點，若點P到直線BC與直線C1D1的距離相等，則動點P的軌跡所在的曲線是（ ）.

A．直線 B．圓

圖2

C．雙曲線 D．拋物線

解：因為點P到C1D1的距離即為點P到C1的距離，所以在平面BCC1B1內，點P到定點C1的距離與點P到定直線BC的距離相等.由圓錐曲線的定義可知，動點P的軌跡為拋物線，故選D.

策略二：交軌法

思路分析：根據題意，畫出圖形，在空間中，AM⊥MC，取AC的中點O,則點M的軌跡是以AC為直徑的球面O.點M是側面BCC1B1內的動點，所以點M是球面O與平面BCC1B1的公共點.則點M在平面BCC1B1內的軌跡是以BC為直徑的半圓（不包含B,C點）.以下同解法1.

解法2：如圖3，在空間中，AM⊥MC，點M是動點，點A,C是定點，取AC的中點O,所以點M的軌跡是以AC為直徑的球面O.

圖 3

又點M是側面BCC1B1內的動點，所以點M是球面O與平面BCC1B1的公共點.取BC的中點N，則ON⊥平面BCC1B1,OB=OC.所以在平面BCC1B1內點M的軌跡是以BC為直徑的半圓（不包含B,C點）.

后續同解法1.

歸納：在平面幾何、解析幾何中已有“交軌法”的運用，若對此有一定的知識遷移能力，則在空間圖形軌跡問題中也可涉及這種重要的思考方法——交軌法，即從集合的“交”來確定兼備有關集合特性的元素.解題基本思路是：先找出符合各條件對應的點的軌跡，然后求出符合各條件對應點的公共部分.即化“動”為“靜”，化“整”為“零”，各個擊破.

變式：在正方體ABCD-A1B1C1D1中，點P在側面BCC1B1及其邊界上運動，總有AP⊥BD1，則動點P的軌跡為.

解：如圖4，連接AC,AB1,B1C，在正方體ABCD-A1B1C1D1中，易證得BD1⊥平面ACB1，所以點P在平面ACB1上.又點P在側面BCC1B1及其邊界上運動，所以點P的軌跡為平面ACB1與平面BCC1B1的交線段CB1.

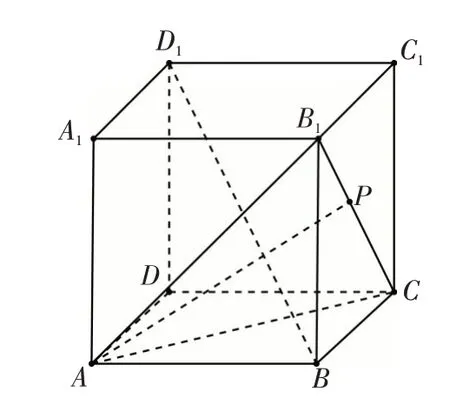
圖4

策略三：空間向量法

思路分析：依題意，四棱柱ABCDA1B1C1D1是正四棱柱，以D為坐標原點，以DA方向為x軸的正方向，建立空間直角坐標系，由已知，設M(a,4,b)(0＜a＜4,0＜b＜23)，因為AM⊥MC，可得點M的軌跡方程：(a-2)2+b2=4，即點M的軌跡是以BC為直徑的半圓（不包含B,C點）.以下同解法一，也可結合圓的參數方程繼續求解.

解法3：依題意，四棱柱ABCD-A1B1C1D1是正四棱柱，以D為坐標原點，以DA方向為x軸的正方向，建立空間直角坐標系，則A(4,0,0),C(0,4,0),設M(a,4,b)(0＜a＜4,0＜b由AM⊥MC，有，得(a-2)2+b2=4.即點M的軌跡方程：(a-2)2+b2=4.因為A1B1⊥平面BCC1B1，所以∠A1MB1為A1M與平面BCC1B1所成角.在RT△A1MB1中，由B1(4,4,23)，M(a,4,b),得B1，設a=2cosθ+2，b=2sinθ,其中0＜θ＜π.得且，所以2≤B1M＜27.又A1B1=4，所以tan∠A1MB1的取值范圍為

圖5

歸納：立體幾何中的動點問題，有些時候如果按立體幾何的傳統方法幾乎無法入手，空間向量巧妙地解決了這一難題，將數與形完美地結合起來，降低了立幾的思維難度，解題有一定的規律性，便于學生掌握.其步驟：①建系；②找點的坐標；③寫出向量坐標；④結合公式進行論證、計算；⑤下結論.不規則的坐標系的建立較為靈活，但還是有“法”可依，平時教學過程中，應加強建不規則坐標系的練習，幫助學生消除心理障礙.

變式：如圖6所示，正方體ABCD-A1B1C1D1中，點M是底面正方形ABCD內的一個動點，若直線C1D,C1M所成的角等于30o，則以下說法正確的是（ ）.

圖6

圖7

以上是幾種方法各有所長，適合求解立體幾何中的動點軌跡問題.一般來說，坐標法比較容易操作，但有時計算繁雜，對于那些不規則坐標系的習題尤其如此；降維法、交軌法技巧性強，但也是有規律可循，平時學習備考中堅持多法并舉，擇優而取，以增強解題的技術水平和效益.