例談變換在高中數學的應用
廣東省廣州市花都區第二中學 楊偉達 510800
在解題教學中,轉化與化歸是一種重要的解題思想,也是一種最基本的思維策略,更是一種有效的數學思維方式.其中變換是轉化和化歸的一種形式,在解題中常常用到.形如變換位置、變換數值、變換視角等,它往往會激起學生的思維火花,開啟數學思維之門,在解題中起到四兩撥千斤的效果.
1 變換位置
有這樣的一類幾何題,直接用傳統方法求解、證明往往比較困難,此時需要轉化思路,在確保原式不變的前提條件下,變換一個位置,問題就會迎刃而解.變換位置常有變換點、變換線、變換角等.
1.1 換點
在等價條件下,用某個點替換另一點達到快速解題.這一方法是在立體幾何中解決線面距離問題時的常規手法.
例1(2019屆廣州市高三年級調研測試19)如圖1,四邊形ABCD是平行四邊形,平面AED⊥平面ABCD,EF//AB,AB=2,BC=EF=1,AE=6,DE=3,∠BAD=60°,G為BC的中點.(1)求證:FG//平面BED;(2)求證:BD⊥平面AED;(3)求點F到平面BED的距離.
分析:利用傳統方法作垂線求點F到平面BED的距離比較困難,不妨利用線面平行的性質,轉移到另一點位置,從而轉化為求另一個點到面的距離(方便求得).再利用等體積法間接求高.
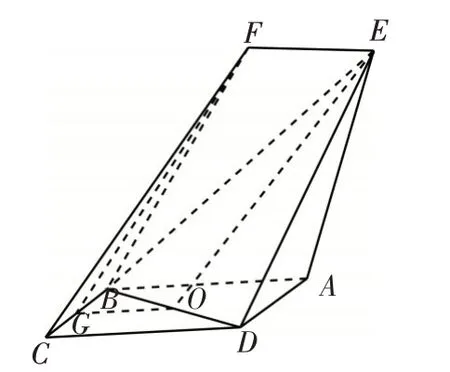
圖1
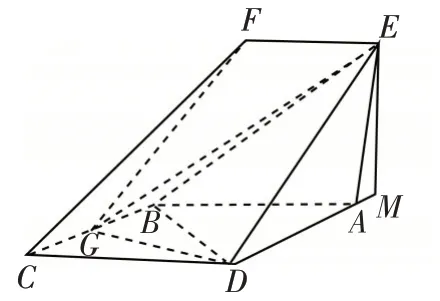
圖2
解:(1)略.(2)略.
(3)如圖2,由(1)FG//平面BED所以點F到平面BED的距離轉化為點G到平面BED的距離,不妨設點G到平面BED的距離為h,過E作EM⊥DA,交DA的延長線于M則EM⊥平面ABG,所以EM是三棱錐E-ABG的高,在△ADE中
1.2 換線
有這樣的一類題,在涉及線段長度之和時,常用某一線段替換另一線段,以直代曲,從而方便解題.比如幾段線段之和求距離的最值問題在幾何試題中時常用到換線.
例2 (2019年廣東一模15)在三棱錐P-ABC中,AP,AB,AC兩兩垂直,且AP=AB=AC=2,若點D,E分別在棱PB,PC上運動(都不含端點),則AD+DE+EA的最小值為_____.
分析:本題考查了立體幾何兩動點問題,涉及兩段或兩段以上的線段之和,通常采用以直代曲即可解決.本題最根本的辦法是轉化為同一平面,找對稱、找全等,替換某線段長度,最終達到兩點間線段最短.
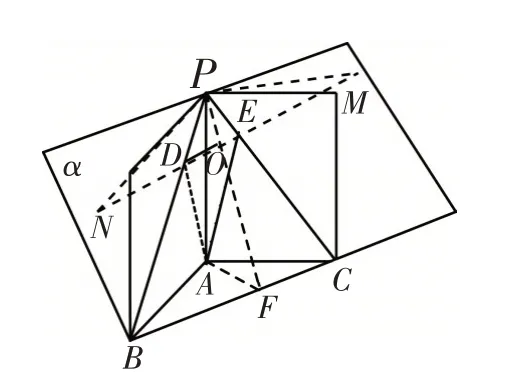
圖3
解:如圖3,點P,B,C確定一個平面α因為AP,AB,AC兩兩垂直,且AP=AB=AC=2所以△PAC,△PAB均為等腰直角三角形,所以∠DPA=∠EPA=45°,BC=2,AF=BF=FC=1.在Rt△PAF中,PF=3,在Rt△PFC中,PF=3,FC=1,所以,所以∠PFC=30°.在平面α內,分別過點P作輔助線PM,PN,滿足PM=PN=2,且∠CPM=∠BPN=45°,由此△PAE?△PME,△PAD?△PND,所以AE=ME,AD=ND,所以AD+DE+EA=ND+DE+EM,當且僅當點N,D,E,M在同一直線時,AD+DE+EA取得最小值,在Rt△POM中,∠OPM=75°,PM=2,OM=同理,ON=PNsin75°=,所以即AD+DE+EA的最小值為
1.3 換角
有這樣的一類題,在等價條件下,通過平移(或者替換)一條線段或兩條線段,達到角的變換,進而可將問題解決.比如空間角轉化為平面角、弦切角、圓周角等等.
例3(2018全國卷2)在長方體ABCDA1B1C1D1中,AB=BC=1,AA1=3,則異面直線AD1與DB1所成角的余弦值為( ).

分析:在涉及求異面直線夾角時,常常平移直線到某一點.解題的策略是異面問題轉化為平面問題,找到平面上的點,進而找到異面直線的夾角.
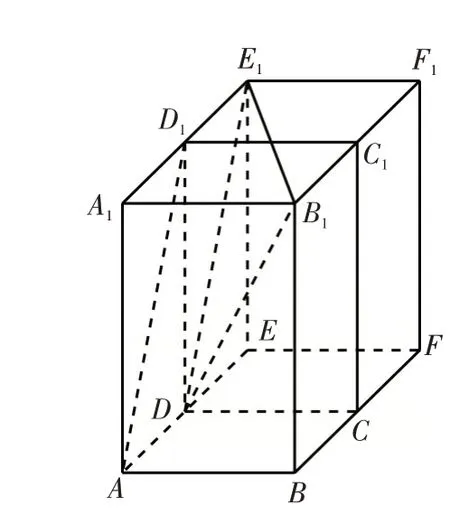
圖4
解:補上如圖4所示的長方體CDEF-C1D1E1F1,連接DE1,B1E1易知AD1∥DE1,則∠B1DE1為異面直線AD1與DB1所成角,在長方體ABCD-A1B1C1D1中,故選C.
2 變換數值
有這樣的一類題,直接解題比較困難,發現與某一結構類似,比對結構,通過缺什么補什么,發現某值可以用另一種形式替換,變換數值后,結構形式齊整,用熟悉的方法即可將問題解決.

分析:可將1替換成sin2α+cos2α,采用弦化切,原式可化為含有正切的函數式,代入,計算,求值.

圖5
3 變換視角
有這樣的一類題,可以從多角度思考,變換視角后,發現這一式子可以用另一個視角去審視、去思考,此時解題就會豁然開朗.比如數形轉換、主元轉換、函數與方程轉換等等,這樣方法就另辟蹊徑,簡單明了,對解題起到事半功倍的效果.
例5(2020花都區高一期末統考)在等


