從幾何特性入手 圓錐曲線巧求解
甘肅省張掖市實驗中學 宮 雪 734000
在高考中,圓錐曲線一般有兩小一大三道題,一直是高考的重點、熱點,也是難點;其中圓錐曲線客觀題主要考查圓錐曲線定義、標準方程、幾何性質(如漸近線、離心率等),滲透了數形結合、轉化與化歸、曲線與方程的數學思想方法,以發展學生的學科素養為導向,考查圓錐曲線的核心知識與本質特性,方法靈活多變,能力要求高,相當一部分學生對此無所適從,戰戰兢兢,下面以2019年高考數學全國Ⅰ卷理科第10題為例,進行知識與解法剖析,旨在拓寬讀者思維視野,提高解題能力.
問題:(2019年全國Ⅰ卷理科第10題)已知橢圓C的焦點為F1(-1,0),F2(1,0),過F2的直線與C交于A,B兩點,若|AF2|=2|F2B|,|AB|=|BF1|,則C的方程為( ).
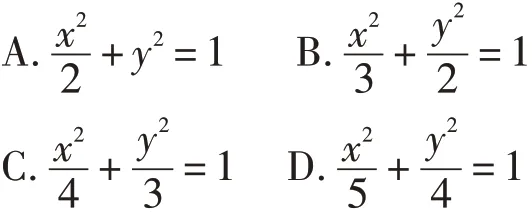
分析:本題表面看來樸素無華,內涵卻很豐富,考查橢圓的定義、標準方程及余弦定理的應用,考查數形結合思想、轉化與化歸、方程的數學思想方法,很好的落實了直觀想象、邏輯推理、數學運算等數學素養,具有很好的創新性;求解圓錐曲線試題,首先考慮畫圖,其次考慮定義與幾何性質,充分挖掘圖形幾何量之間的等量或相互關系,凡涉及焦點三角形的問題,還應注意解三角形等知識的應用.
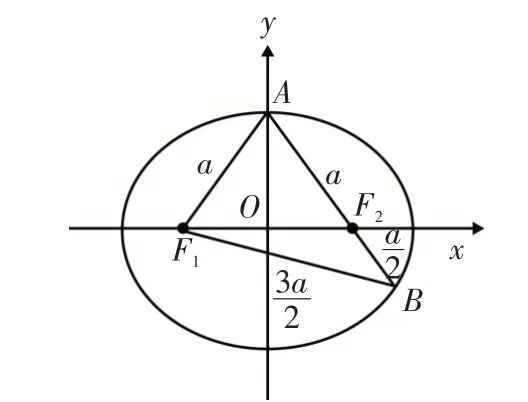
圖1


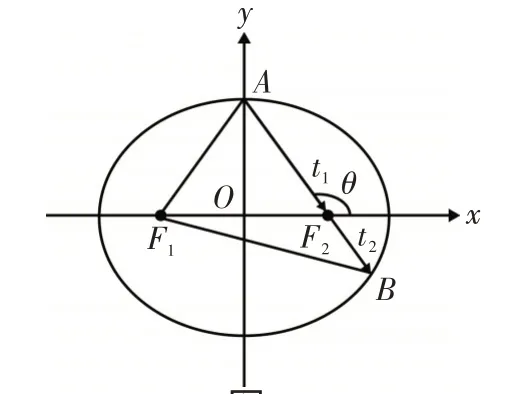
圖2

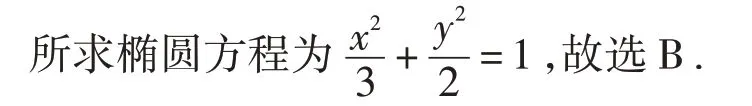

圖3
若A,B為直線l上兩點,其對應的參數分別為t1與t2,線段AB的中點為M,點M對應的參數為t0,則以下結論經常用到:①重在數形結合,理解記憶,切忌生搬硬套,牽強附會.
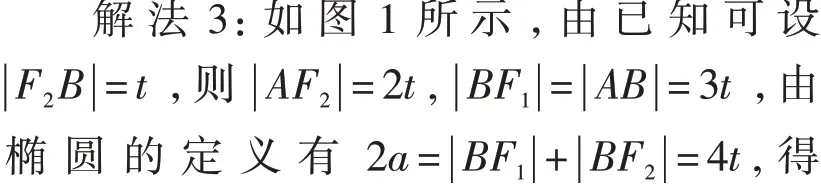

點評:靈活應用余弦定理是解題的關鍵,此方法也可換做在△F1F2B與△AF1B中求∠ABF1的余弦值.



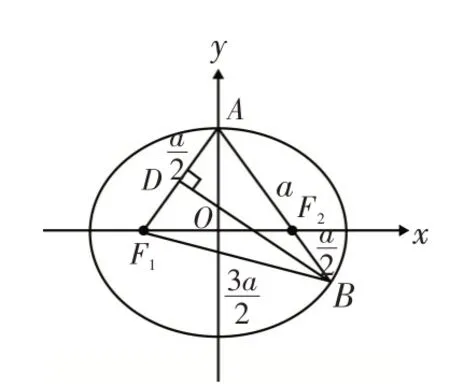
圖4
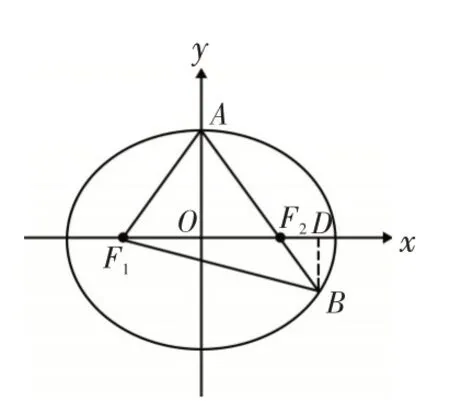
圖5
解法6:如圖1所示,由已知可設|F2B|=t,則|AF2|=2t ,|BF1|=|AB|=3t,由橢圓的定義有2a=|BF1|+|BF2|=4t ,得又因為|AF1|+|AF2|=2a,所以|AF1|=a,所以點A應為橢圓C的上頂點(或下頂點);如圖5所示,過點B作BD垂直x軸于點D,則△AOF2∽△BDF2,相似比為2:1,得(a>b>0)上,所 以 滿 足 其 方 程 得:b2=2,所求橢圓方程為,故選B.解法7:如圖1所示,由已知可設|F2B|=t,則|AF2|=2t ,|BF1|=|AB|=3t,由橢圓的定義有2a=|BF1|+|BF2|=4t ,得又因為|AF1|+|AF2|=2a,所以|AF1|=a,所以點A應為橢圓C的上頂點(或下頂點);如圖6所示,由焦半徑公式得,其中e為橢圓的離心率,p為焦點到準線的距離(簡稱:焦準距),右準線方程為:為直線AB的傾斜角;又因為得a2=3,又因為c=1,所以b2=2,所求橢圓方程為
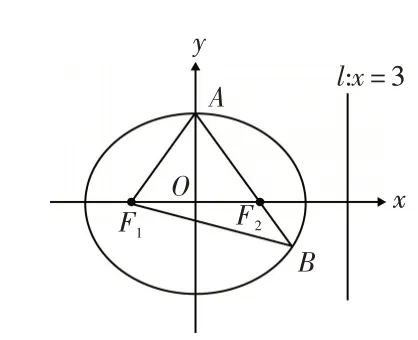
圖6
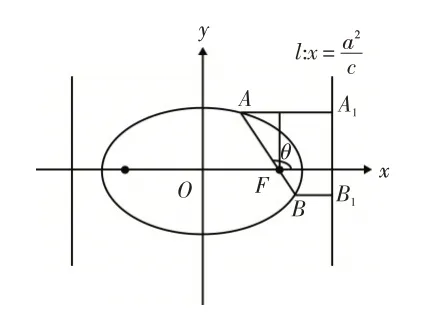
圖7
點評:用焦半徑公式幾乎就是秒殺此類試題;焦半徑公式的推導如下:橢圓的第二定義是平面上到定點F(c,0)(F不在l上)的距離與到定直線(橢圓的右準線)的距離之比為常數e(0<e<1)的點的軌跡為橢圓(注:人教A版選修2-1第50頁).如圖7所示,AB是過橢圓的右焦點F(c,0)的一條弦,它的傾斜角為θ,p為焦點F(c,0)到準線的距離(簡稱:焦準距),過A做AA1⊥l于點A1,過B做BB1⊥l于點B1,則由第二定義得:|AF|=e|AA1|=e(p+|AF|?cosθ),所以同理:
大部分學生對圓錐曲線試題有畏懼情緒,究其主要原因還是找不到解題的突破口或切入點,但從以上解析可以看出,抓住圖形的某一幾何特性,去轉化、求解圓錐曲線試題,讓學生在較短的時間內,突破思維障礙,快速準確地求解題目,事半功倍;另一方面,一題多解是提高解題能力的有效途徑,它在呈現不同解法的同時,不但拓寬了學生思維的靈活性與深刻性,而且提高了學生解題的興趣、品味、效率.

