頁巖可壓裂性聲學模型及應用?

李 帆 巴 晶 符力耘 檀文慧 于 庭 曹青業

(1 河海大學 南京 211100)

(2 中國石油大學(華東)地球科學與技術學院 青島 266580)

0 引言

頁巖氣作為一種非常規能源，儲層致密，孔隙度低，滲透率極低，結構和富集條件比較復雜[1]，具有易發現、難開采的特點。頁巖氣的這些特點使得頁巖氣的勘探和開發的難度及風險加大。因此，需要采取水力壓裂增產改造措施，以便獲得進一步的工業化產能，故研究頁巖儲層可壓裂性就顯得尤為關鍵。

近年來相關研究人員相繼提出了新方法評價頁巖儲層可壓裂性，為頁巖儲層可壓裂性評價開辟了多種思路，同時也為頁巖儲層開采提供了更多前期指導。Chong等[2]將脆性指數作為評價頁巖可壓裂性的唯一有效指標，脆性指數越高，可壓裂性越好，為頁巖可壓裂性評價提供了新思路。李慶輝等[3]進行了頁巖儲層脆性的綜合評價，為評價可壓裂性做鋪墊，但量化以后的脆性評價可壓裂性考慮的因素單一，不能全面反映頁巖可壓裂性的綜合特征。因此，在評價頁巖可壓裂性強弱時不單是要考慮脆性的大小，而且還要考慮斷裂韌性的強弱、天然裂縫、地應力環境等其他影響因素。為此，相關人員相繼提出了許多方法來評價頁巖儲層可壓裂性。Breyer[4]認為頁巖可壓裂性與材料韌性和脆性相關，可以用楊氏模量和泊松比來表征。唐穎等[5]利用相關影響因素標準化值與權重系數加權得到了頁巖儲層可壓裂性評價的數學模型。袁俊亮等[6]從頁巖儲層脆性指數、斷裂韌性以及巖石力學特性等三個方面為出發點考慮，建立了新的頁巖儲層可壓裂性評價方法。李文陽[7]等提出頁巖儲層可壓裂性是頁巖氣“甜點”選擇過程中的重要因素之一，主要是評價裂縫和層理、水平應力差、頁巖脆性等儲層參數。廖東良等[8]在使用礦物組分計算巖石脆性的同時引入斷裂韌度作為每種礦物的加權系數，建立了新的脆性指數計算模型。侯冰等[9]考慮了地質評價、頁巖體積壓裂評價以及工程技術評價建立了適合中國地質情況的可壓裂性評價模型。高輝等[10]結合儲層脆性指數以及斷裂韌性指標提出了一種頁巖儲層可壓裂性評價方法。

調研國內外頁巖可壓裂性評價方法顯示，目前國內評價頁巖可壓裂性主要還是考慮單一影響因素，從而難以準確地評價頁巖儲層可壓裂性。本文在結合頁巖脆性評價方法和斷裂韌性指標的基礎上，提出一種表征頁巖可壓裂性的評價方法。基于超聲波實驗測量，分析頁巖儲層的聲學特征，然后利用疊前反演技術，結合傳統的基于彈性參數的脆性指數與新的可壓裂性評價方法進行脆性反演預測，然后結合實際工區資料，對比分析新的可壓裂性評價方法預測結果與實際儲層產氣結果。

1 頁巖儲層特征分析

1.1 工區概況

本文研究渝東南某工區頁巖氣藏，位于齊岳山斷裂以西、四川盆地內部的川東南斷褶帶內，目的層X 層為深水陸棚相沉積，發育巖石類型以暗色富有機質泥頁巖為主，筆石類生物化石豐富。

1.2 目的層巖樣特征

1.2.1 有機質特征

本文通過對目的層取心段進行了總有機碳(Total organic carbon,TOC)含量測試，選取82個巖石樣品，其中TOC 1%的樣品為39個，TOC 2% 的樣品為12個，總體表明研究區目的層頁巖有機質含量高。

從圖1(a)可知TOC隨石英含量的增大而增大，兩者具有正相關趨勢，說明研究區目的層頁巖硅質礦物可能為生物成因[11]。相反，TOC與黏土含量相關性較差，如圖1(b)所示，證明了TOC 主要分布于石英粒間孔中。圖1(c)中黃鐵礦和TOC 之間也具有較好的正相關關系，表明黃鐵礦和有機質之間可能具有成因聯系[12]。因此研究區目的層層段可考慮依據石英含量和黃鐵礦含量的分布來判斷TOC的分布情況。

1.2.2 物性特征

對研究區目的層22 塊樣品進行了氦氣孔隙度測試，測試結果顯示孔隙度值分布在0.81%～4.02%之間，平均值為1.74%。滲透率值分布在(0.0013～0.004)×10?3μm2之間，平均值為0.0024×10?3μm2。

當頁巖氣儲層TOC 含量處于低值區時，孔隙度隨著TOC 含量的增加而快速增加，這是由于有機質孔快速增加引起的。如圖2(a)所示，當TOC含量小于1.5%時，孔隙度快速增加。但隨著TOC 含量的繼續增加(TOC>1.5%)，有機質會發生碳化，此時有機質孔孔隙會被壓縮和其他礦物充填，導致儲層總孔隙度減小，增長變緩。如圖2(b)所示，孔隙度會隨著密度的增大而減小。由于TOC 的密度低，所以當儲層中TOC 含量增加時，孔隙度會相應增大，密度則會降低。

1.3 超聲波實驗及聲學特征

1.3.1 超聲波實驗

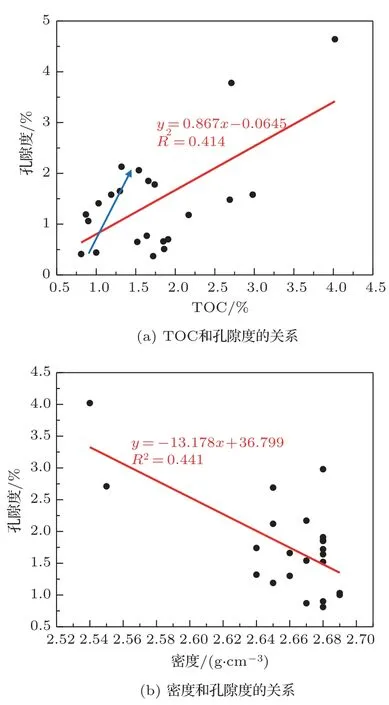
圖2 頁巖樣本TOC、密度和孔隙度的關系Fig.2 TOC and density vs porosity of shale samples

本文選取研究區目的層頁巖樣本，采樣覆蓋儲層段的主要巖性變化，共采82塊樣本，巖心樣本的直徑均為25 mm，高度在35～70 mm之間，斜度小于0.05 mm 的柱塞樣品，進行相關的地震巖石物理測試。

進行巖石干燥條件下的巖石物理測試時，為了使樣品能夠達到相對“干燥”條件，需要先將樣品在溫度為60?C 的烘箱中均勻烘干48 h 以上，然后再將烘干后的樣品在潮濕空氣中露天放置24 h 以上得到約含有2%～3%水分的“干燥”樣品以消除黏土礦物脫水對巖石骨架的破壞作用[12]。利用超聲脈沖透射測得樣品的速度，實驗中，壓力從0 MPa加壓至55 MPa，間隔5 MPa 測試一次，壓力點測量間隔10 min以上并保證圍壓平衡，壓力偏差小于0.3%。此次測試均為平行于層理巖石樣品的速度。速度測量相對誤差的量級縱波約為0.23%，橫波約為0.16%。

1.3.2 聲學特征

本次研究針對采集的43 塊巖心樣品進行了不同壓力速度測試，壓力5 MPa～55 MPa，間隔5 MPa。實驗采用與Guo等[13]相同的實驗裝置，基于超聲波脈沖法測量巖石樣本中的縱橫波速度。系統主要由高壓容器、溫度控制單元、圍壓控制單元、孔隙壓力控制單元、聲波參數測試單元組成，具有溫度、圍壓、孔隙壓力等控制功能。圖3 分別是研究區樣品縱橫波速度隨有效壓力(圍壓減去孔隙壓力)的變化曲線，從圖中可以看出，巖心測試縱波速度變化范圍在4200～6000 m/s，橫波速度范圍在2600～3400 m/s。從速度變化形態上來看，當壓力在30 MPa～40 MPa 之間時縱橫波速度迅速增加，在超過該壓力時縱橫波速度變化較小，并與壓力成近似線性關系，因此可以認為使研究區巖石中微裂隙閉合的有效壓力應在30 MPa～40 MPa 以上，對于研究區的高孔壓區，可以認為微裂隙在地層中是未完全閉合的[14]。對比測試的巖心速度與測井數據，實驗室測試數據與井測試數據從儲層上到下變化趨勢一致，先減小后增大，速度較小的層段對應儲層較好的層段。

對研究區的巖心樣品進行密度測試，從測試結果來看該區域的密度主體分布在2.6～2.7 g/cm3之間。巖石儲層礦物成分、孔隙度以及孔隙流體都會影響儲層密度的變化趨勢，分析密度與速度及其他彈性參數之間的關系可為儲層脆性預測及描述提供支持。

如圖4 所示，從密度分布形態來看，密度主體分布于2.6～2.7 g/cm3之間，有個別樣品密度大于2.7 g/cm3，泊松比大于0.25，結合礦物成分分析為鈣質含量較高造成。隨著密度的增大，縱波速度、楊氏模量、體積模量以及剪切模量均呈現增大的趨勢，且呈現較好的正相關關系，橫波速度、泊松比、縱橫波速度比以及拉梅常數也呈現增大的趨勢，但相關性較差。

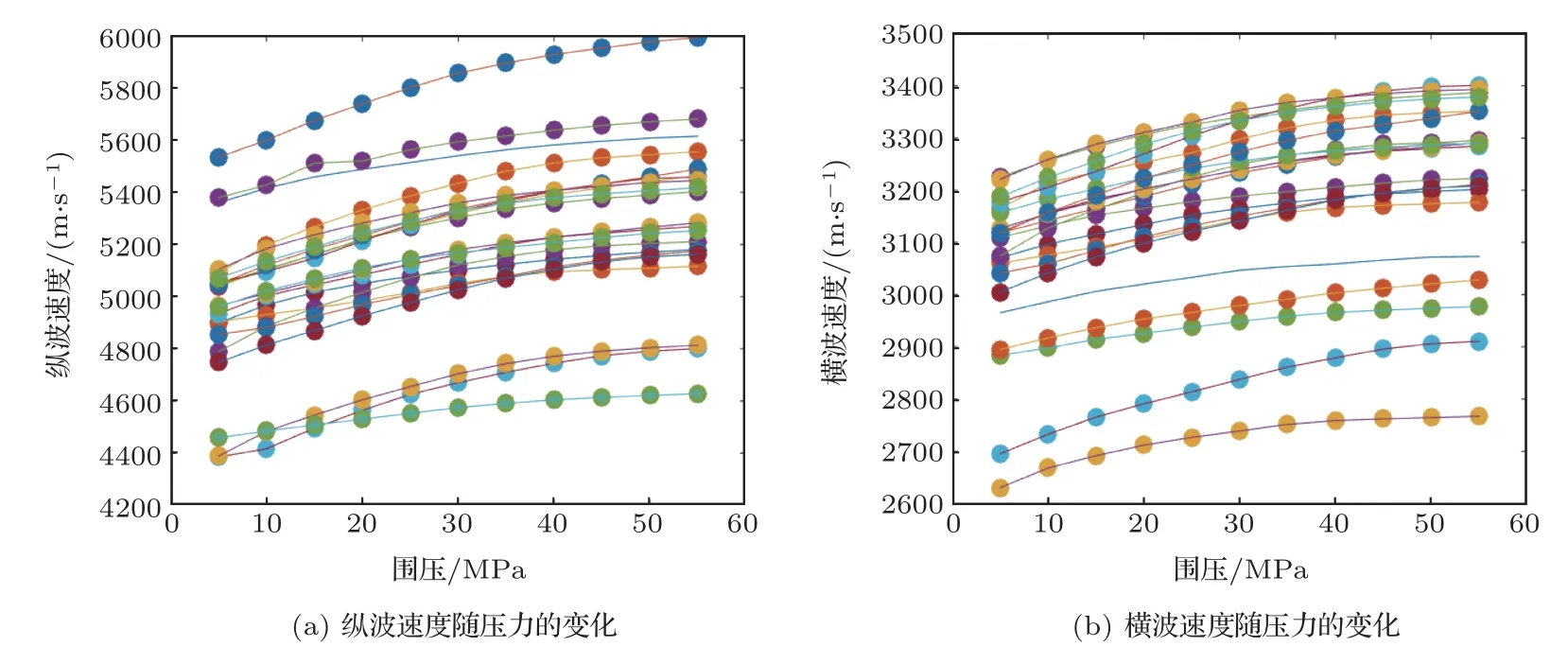
圖3 頁巖樣品縱橫波速度隨有效壓力的變化Fig.3 Velocities of P and S waves vary with the effective pressure of shale samples

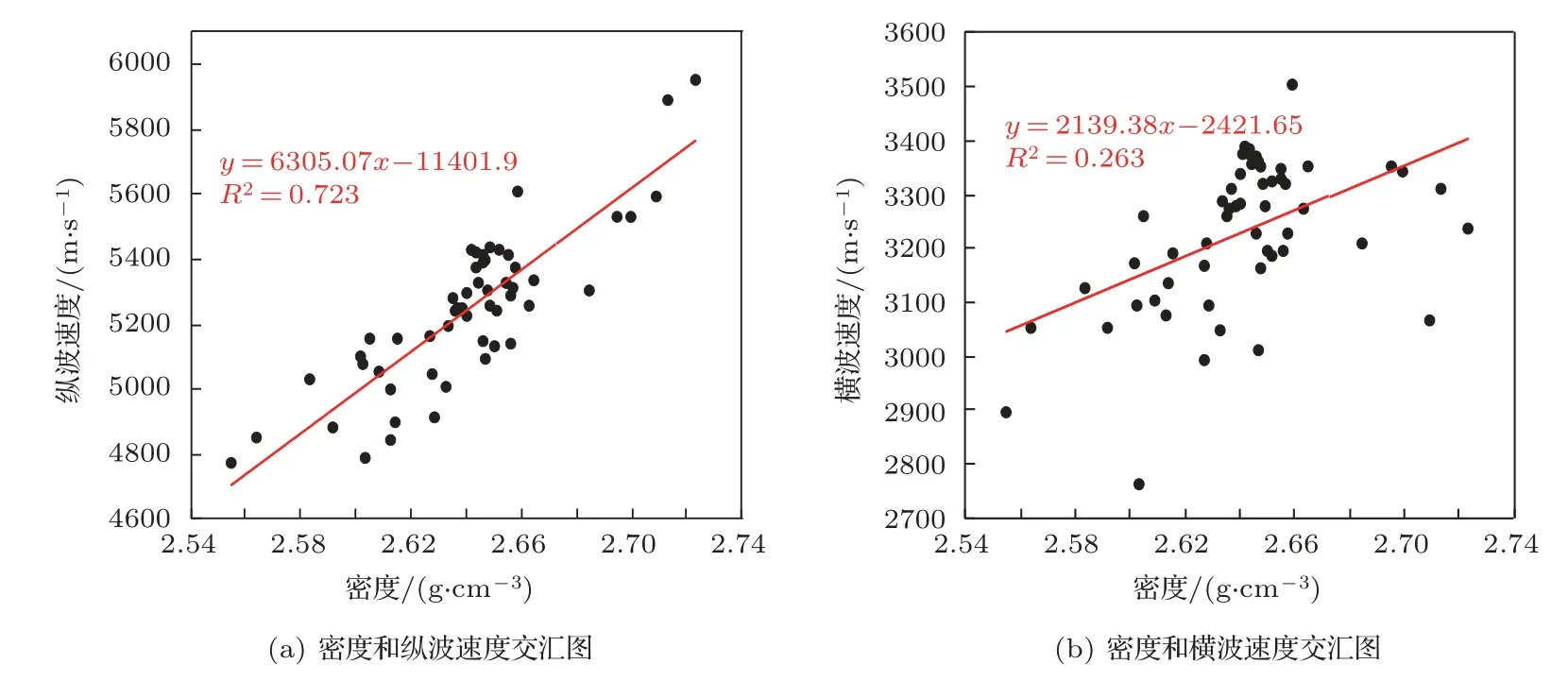
圖4 頁巖儲層密度和彈性參數之間的關系Fig.4 Relation of shale reservoir density and elastic parameters

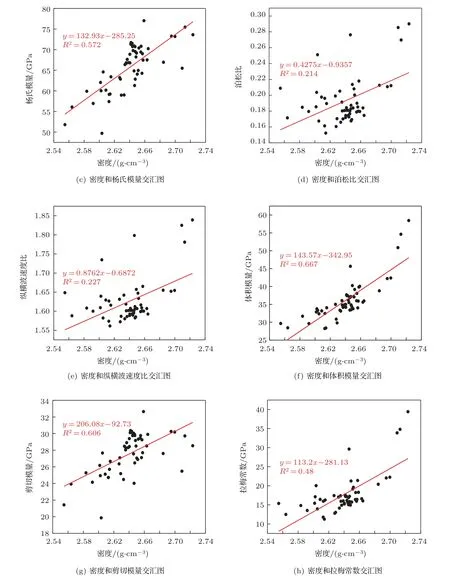
圖4(續)頁巖儲層密度和彈性參數之間的關系Fig.4 (continue)Relation of shale reservoir density and elastic parameters

2 構建新的可壓裂性模型

2.1 基于彈性參數的脆性評價模型

研究認為，巖石力學實驗過程改變了巖石的初始形態，使巖石樣本經歷了裂縫閉合、形成、擴展等階段，微裂紋損傷影響了巖石的強度和變形，通過室內力學實驗測量最終獲得的靜態楊氏模量和靜態泊松比參數也會因此產生可能的異常，而巖石超聲波測試屬于無損測試，其測量過程中巖石樣本相對于初始狀態未發生改變，且變形時間短。Guo 等[15]采用楊氏模量和泊松比的比值作為脆性因子。綜合以上考慮，本文采用Guo 等提出的脆性因子，計算動態楊氏模量(Ed)與動態泊松比(νd)的比值BI1。

巖石彈性參數分為靜態彈性參數和動態彈性參數，靜態彈性參數是利用巖石樣本靜態加載，測量其形變量計算得到；動態力學參數則是通過聲波在巖石樣本的傳播速度信息轉換得到[16]。利用式(1)、式(2)結合頁巖樣本密度、縱波速度、橫波速度等參數可分別計算頁巖樣本動態楊氏模量Ed和動態泊松比νd，進而得到脆性指數。

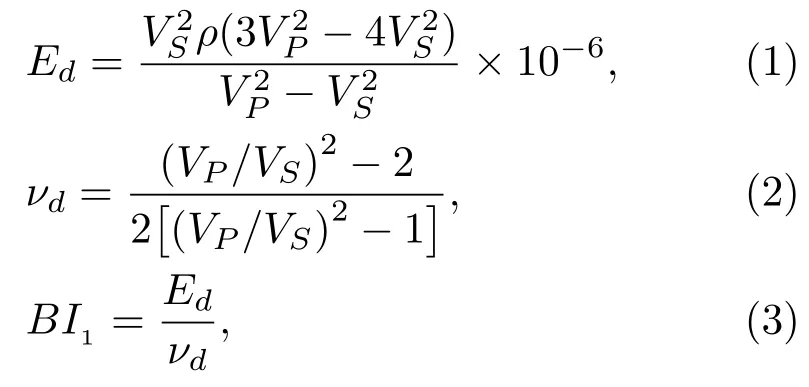
其中，VP、VS分別為縱波速度、橫波速度，單位為m/s；ρ為密度，單位為g/cm3。

脆性評價結果的巖樣動態楊氏模量、動態泊松比交匯圖如圖5所示，隨著楊氏模量增大，泊松比減小，巖石脆性指數整體上呈現增大的趨勢(圖中箭頭所示方向)，但分布較為分散，這與地層所受壓力有關，一般認為圍壓越大，增大趨勢更集中。

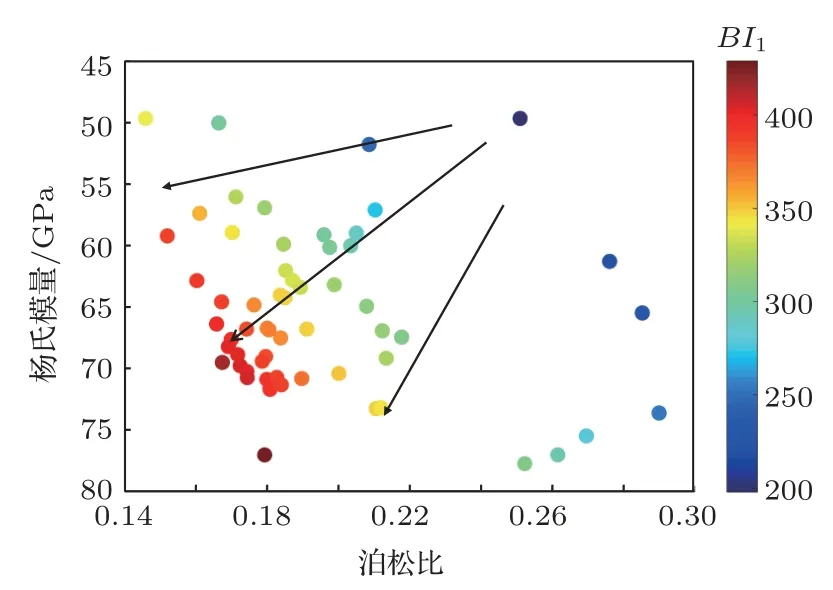
圖5 巖樣動態楊氏模量、動態泊松比表征的巖石脆性Fig.5 Rock brittleness characterized by dynamic young’s modulus and dynamic Poisson’s ratio

2.2 斷裂韌性指標

斷裂韌性會影響頁巖儲層受壓破裂時裂縫的延展性。因此，在評價頁巖可壓裂性強弱時不僅要考慮脆性的大小，還要考慮斷裂韌性的強弱。從巖石力學方面來看，天然裂縫、地應力環境等影響頁巖可壓裂性的其他因素，可以被認為其影響由巖石脆性或斷裂韌性。

根據前人的研究，張開型斷裂韌性與巖石動態楊氏模量、單軸抗拉強度、縱橫波速度以及圍壓等參數存在函數關系。其中，陳治喜等[17]研究發現，頁巖儲層張開型斷裂韌性(KC)與動態楊氏模量(Ed)存在函數關系如下：

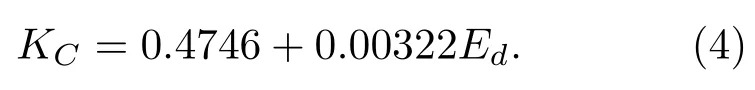
2.3 可壓裂性評價的數學模型

Rickman 等[18]最早使用歸一化后的靜態楊氏模量、泊松比的加權平均值BI2來表征巖石脆性，目前該方法仍然是業界評價頁巖脆性使用最為便捷、廣泛的方法。具體歸一化方法將需要被歸一化的指標分為正向和逆向兩種，正向指標指數值盡可能大為好，而逆向指標指數值盡可能小為好，計算公式參考式(6)。該類脆性評價方法中，脆性指數楊氏模量為正向指標，而泊松比為逆向指標，如下：

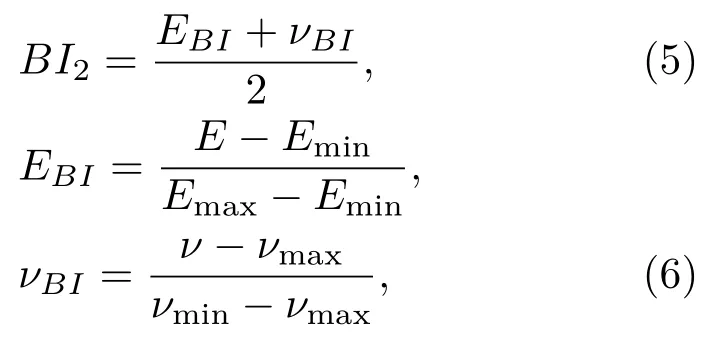
其中，E為巖石的楊氏模量，單位GPa；ν為巖石的泊松比，無量綱；EBI為歸一化的楊氏模量，νBI為歸一化的泊松比；Emax、Emin分別為統計范圍內巖石楊氏模量的最大值、最小值；νmax、νmin分別為統計范圍內巖石泊松比的最大值、最小值。

可壓裂性指數作為表征可壓裂性強弱的指標，首先將脆性指數與斷裂韌性指標進行歸一化得到無量綱表達式，然后采用層次分析法判斷兩者對于可壓裂性的重要程度，并將具體系數量化，最后將歸一化數值及影響系數進行加權計算，獲得可壓裂性指數：

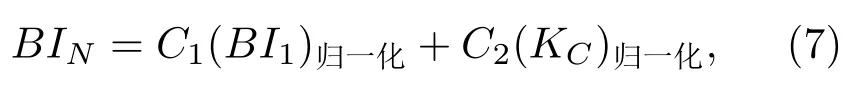
式(7)中，BIN為可壓裂性指數，BI為脆性指數，C1為BI的影響權重系數，C2為KC的影響權重系數。將式(3)、式(4)帶入式(7)可得

2.4 權重系數的確定

頁巖脆性與斷裂韌性對于可壓裂性的重要性不一致，因此需要分別確定二者權重系數來確定計算可壓裂性指數，可采用層次分析法來確定二者對于可壓裂性的影響程度的參數。首先確定巖石脆性和斷裂韌性對于頁巖儲層可壓裂性的影響程度的相對重要性。

層次分析法將一個復雜問題轉化為目標、準則和方案等層次，然后進行定量和定性分析，通過對復雜本質和相關影響因素深入分析后，繪制清晰的層次結構圖并進行判別預測。按照層次分析法遞階層次原理，結合工區地質情況，確定巖石脆性和斷裂韌性對于頁巖儲層可壓裂性的影響程度的相對重要性并給出標度，其判斷準則按一定的標度進行設定[19]。

對巖石脆性、 斷裂韌性進行標度賦值(如表1 所示)，并構造判斷矩陣，采用方根法求解判斷矩陣的最大特征值所對應的特征向量為(1.73205,0.57735)，對特征向量做歸一化處理后得到權重向量C=(0.75,0.25)。因此，頁巖儲層可壓裂性影響因素巖石脆性、斷裂韌性的權重系數分別是0.75和0.25，即C1=0.75，C2=0.25。

表1 頁巖儲層可壓裂性評價判斷矩陣因素賦值Table 1 Assignment of judgement matrix factors for fracturing evaluation of shale reservoirs

將C1、C2數值帶入式(8)得

3 頁巖儲層預測應用

在工區內選取一條過井二維地震測線。采用疊前反演方法進行相關彈性參數反演，利用疊前反演得到的泊松比、楊氏模量參數結合頁巖儲層可壓裂性評價方法BI2和BIN分別計算脆性指數和可壓裂性指數，并分別提取脆性反演剖面和可壓裂性反演剖面做結果對比分析。

3.1 彈性參數反演

由 過DY2 井—DY5 井—DY4-V井連井剖面(圖6)可知，反演出的泊松比、楊氏模量對研究區域頁巖儲層具有不錯的區分度，橫向連續性較好，楊氏模量的縱向分辨率較好。

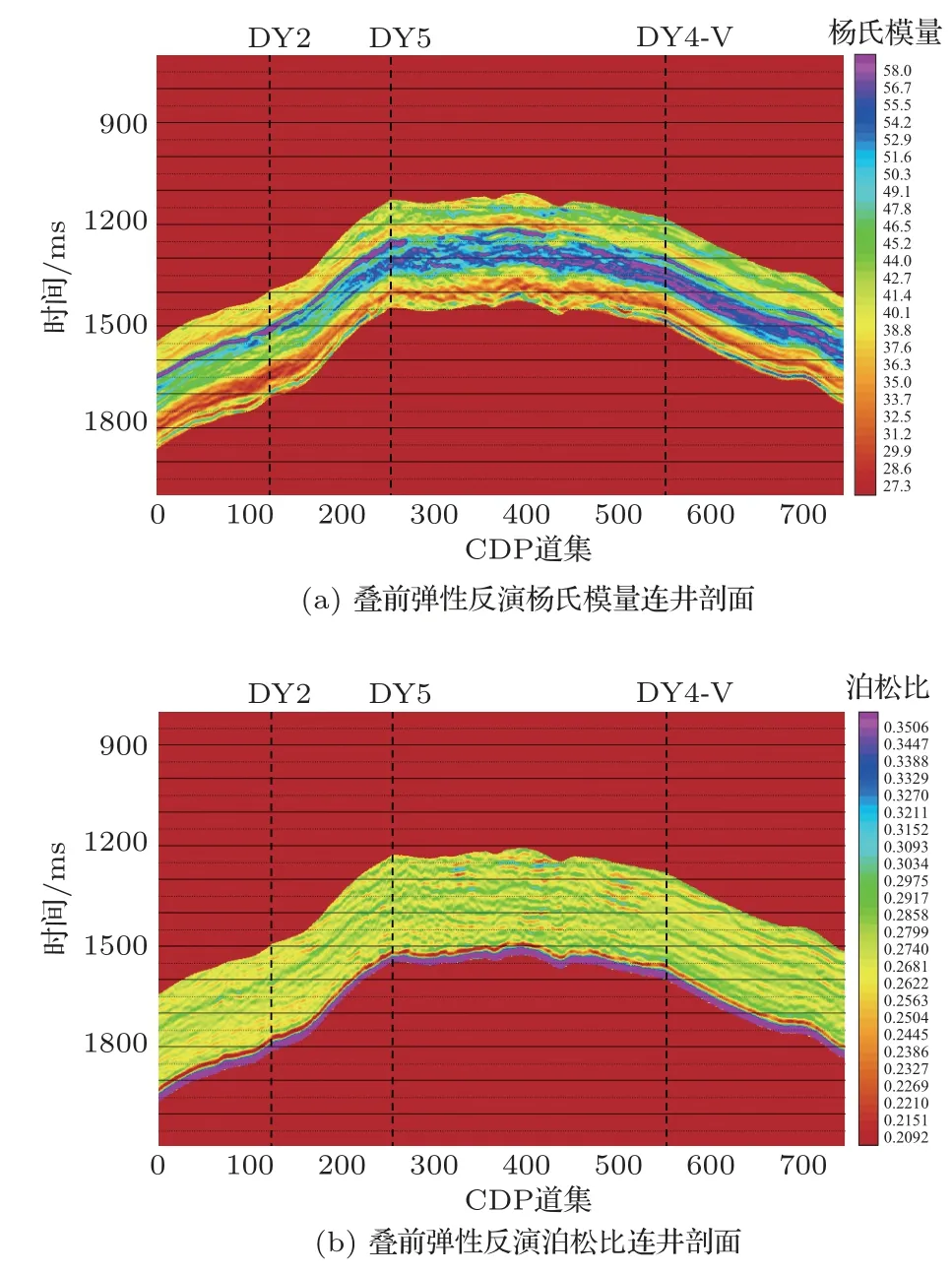
圖6 疊前彈性參數反演得到的楊氏模量和泊松比連井剖面Fig.6 Young’s modulus and Poisson’s ratio well profile obtained by inversion of pre-stack elastic parameters

3.2 脆性指數及可壓裂性指數

利用BI2方法及BIN方法作為計算模型，分別計算研究區域頁巖儲層脆性指數及可壓裂性指數。

BI2與BIN方法反演脆性指數及可壓裂性指數DY2 井—DY5 井—DY4-V 井連井剖面如圖7 所示，脆性指數BI2與可壓裂性指數BIN反演結果具有較好的一致性，且自上而下都具有較好的成層性。對比兩種評價方法結果剖面可知，總體上新方法BIN計算結果對于研究區域測線頁巖儲層可壓裂性的分辨率較好。

3.3 可壓裂性預測效果分析

為了更好地分析、對比兩種頁巖儲層可壓裂性評價方法反演結果對于實際工區儲層可壓裂性預測的效果，首先利用BI2與BIN方法作為計算模型分別得到整個工區的脆性及可壓裂性分布情況，然后截取脆性、可壓裂性反演剖面上分辨率較高的井，對比分析目的層頁巖的反演結果與頁巖氣實際產能(表2)。

圖7 BI2 與BIN 反演脆性及可壓裂性連井剖面Fig.7 BI2 and BIN inversion of the brittleness and fracability continuous well profile

表2 目的層頁巖產氣情況Table 2 Gas production from shale in the target layer

如圖8所示，選取DY4-V井和DY5井在目的層處的脆性及可壓裂性指數計算結果剖面。結果顯示，目的層處新的頁巖儲層可壓裂性評價方法BIN計算的儲層可壓裂性指數要明顯大于BI2方法計算的脆性指數。

BI2與BIN兩種頁巖儲層可壓裂性評價方法計算的脆性及可壓裂性指數均可用于預測儲層可壓裂性好壞，儲層脆性指數或可壓裂性指數越高，儲層可壓裂性越好，儲層越容易被壓裂形成有效網狀裂縫。根據BI2與BIN兩種頁巖儲層可壓裂性評價方法反演所得脆性、可壓裂性指數，以及圖中目的層脆性、可壓裂性指數對比，結合表2 頁巖儲層實際產氣情況可知，BIN方法更適用于描述研究區頁巖儲層的可壓裂性。

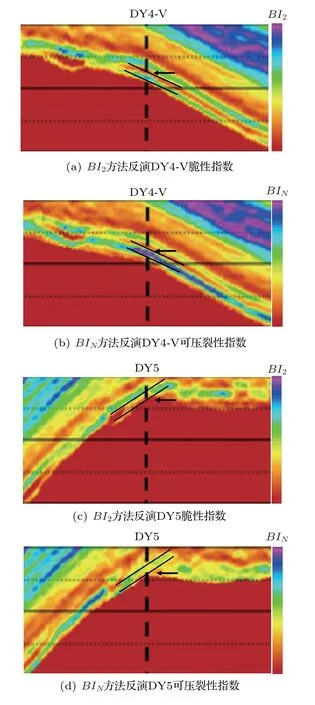
圖8 BI2 與BIN 方法反演目的層處脆性及可壓裂性Fig.8 Methods BI2 and BIN invert the brittleness and fracability at the target layer

4 結論

本文主要對頁巖儲層可壓裂性評價方法及其影響因素進行研究，利用彈性參數的脆性因子，結合巖石的斷裂韌性指標建立了新的可壓裂性評價方法，基于超聲波實驗測量分析頁巖儲層的儲層特征及聲學特征，然后利用新模型對實際工區進行可壓裂性預測，并與前人脆性模型預測結果進行對比，得到以下結論：

(1)分析礦物組分、物性參數之間的關系，結果顯示有機質含量TOC 與石英和黃鐵礦具有較好的正相關關系，與黏土含量沒有明顯的關系，因此研究區目的層層段可考慮依據石英含量和黃鐵礦含量分布來判斷TOC的分布情況。基于超聲波實驗，分析影響因素對巖石脆性的影響，并且根據實際資料對聲學特征進行描述。

(2)基于彈性參數構建的脆性因子并結合巖石斷裂韌性指標，提出一種頁巖儲層的可壓裂性評價指數。利用疊前地震反演方法，采用經典的脆性評價方法與新的可壓裂性評價模型進行可壓裂性預測，結果顯示新的可壓裂性評價模型與實際工區產期結果一致性較好，描述更為精細。新的可壓裂性模型能夠更精確地預測頁巖儲層可壓裂性，在未來不同地區的頁巖氣工程實踐中將有較好的推廣應用價值。