軍事目標關系的擬合地勢及雙重保凸可視建模

王家潤，孫禹楠，尹 輝，楊志龍

華北計算技術研究所 基礎三部，北京100083

1 引言

隨著互聯網技術的迅猛發展，國家及軍隊的網絡安全日益重要，網絡態勢可視化也成為研究熱點[1-2]。不僅如此，在軍事作戰戰場綜合態勢中，軍事目標之間內部復雜抽象的邏輯關系（通信、指揮、作戰編隊、目標跟蹤等）可視化，已成為戰場態勢感知的關鍵，也已成為戰場態勢可視化的重點研究內容，深度揭示敵方的作戰意圖，從而整體提升軍事作戰的決策水平。

網絡可視化一般轉換成圖的node-link 表達[3]，重點是自動布局算法[4]及圖的繪制美學標準研究[4]，在軍事場景中，還需要考慮目標的三維空間真實位置約束。文獻[5]中，通過建立IP與經緯度的映射，以互聯網目標的分層層次作為邏輯高度，建立賽博空間與三維地理空間的一一映射，但缺失真實的高度信息。文獻[6]中，對互聯網節點基于節點的地理位置約束進行了網絡拓撲可視化，并在三維數字地球上進行可視，地面上節點之間采用近似拋物線表達連接關系，但沒有考慮地面的起伏對連線的影響。文獻[7]中，美軍軍用編輯工具MOLE 中對軍事目標進行了視覺上的重排，實際的地理位置采用錨點，顯示位置與真實位置通過虛線相連，地理范圍采用包絡輔助顯示，如圖1 所示，但沒有討論三維顯示。

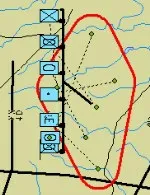
圖1 MOLE：錨點、地理范圍凸包線等效果

在軍事地形顯示中，文獻[8]對線貼地采用LOD 及道格拉斯-普克算法化簡曲線等進行了處理，并對zfighting 閃爍現象進行深度偏移減弱，高程采樣計算量較大，而且針對地形起伏變化劇烈的區域，完全貼地會引起視覺上的抖動感及破碎感。文獻[9]中，采用經典的陰影錐技術，實現線面與地面的像素級融合，而且只能處理單色。文獻[10]中，對交通道路網的繪制采用高度增加偏移量及垂直墻的顯示策略，避免了考慮地形起伏的影響，但顯示位置發生了變化。文獻[11]中，在三維球上，對航空飛行路線的繪制采用B 樣條邊綁定、BumpMapping 技術、GPU Shade 等繪制，效果較好，但對地理位置的高度信息沒有考慮。文獻[12]采用濾波策略，可提取出地形起伏特征，一定程度上可消除地形劇烈起伏的影響。文獻[13]采用梯度提取高程采樣點的方法，可提取出地形起伏特征，消除地形劇烈起伏的影響。文獻[14]將高程采樣，提取地形起伏關鍵點，并采用B樣條曲線擬合，實現標號的跨掠式顯示。

目前網絡可視化軟件ECharts、Gephi、D3、FireEye、FORG3D、Pajek、Cytoscape[15]等，網絡可視化布局算法及動態效果等較好，但是在三維顯示中，沒有考慮地形影響。軍事標號的貼地繪制方法主要為在提取地勢的基礎上，對點集進行一定的處理，消除地形劇烈變化的影響，得到貼合地勢的標號繪制，但是保留了地勢的不斷起伏變化。

本文面向軍事作戰領域，重點考慮三維虛擬戰場中地形起伏的影響，并借鑒圖的美學標準原則，提出了軍事目標關系的保凸三維可視化。主要創新點：

（1）設計了融合、替換及剔除策略，采用凸包算法[16-17]，優選出保凸特征點集，抽取出地形起伏主體趨勢特征，消除了隨地勢的不斷起伏變化。

（2）設計了保凸的Bézier 控制點[18-22]的幾何構造方法，通過逐段連續插值光滑，實現整條曲線的保凸可視化。

2 軍事雙目標單一關系的保凸可視化

2.1 基本說明

研究兩個目標之間的單一關系的三維可視化，軍事目標群體的多重關系三維可視化可分解為兩個目標之間的單一關系可視化。

定義（保凸特征點集）指兩個目標之間繪制的連接曲線上的點集（含兩個端點），是兩目標之間連接曲線可視化的幾何構建要素點集。通過保凸特征點集，依次連接各點，實現兩個目標之間關系的三維可視化。

2.2 算法流程圖

雙目標單一關系可視化流程圖如圖2。

2.3 算法描述

三維坐標采用WGS-84地心坐標系，地球質心為坐標原點，位置描述：經度、緯度、高度。

輸入：

大范圍判定閾值Delta；高程采樣率Rate；曲線光滑采樣數Num ；球面弧最大高度Height ；視覺偏移調整量Modify；兩個目標點AO、BO 的地理位置信息。

過程：

步驟1 構建兩目標虛擬參考線。

將地球中心點EC 與目標點AO 相連，形成線段ECAO；將地球中心點EC 與目標點BO 相連，形成線段ECBO ，參見圖3（AS 、BS 對應的海平面點；AG 、BG 對應的真實地面點；AN 、BN 對應的新點）。該步主要是建立與兩個目標點AO、BO 對應的海平面點、地面點等參考信息。

步驟2 虛擬參考線夾角計算。

計算線段ECAO 與線段ECBO 的夾角angle，如果angle ＞Delta，則AO 與BO 兩目標相距較遠（默認大于1 000 km，短程彈道導彈的射程范圍上限），采用大范圍繪制算法，轉到步驟3；否則，轉到步驟4。

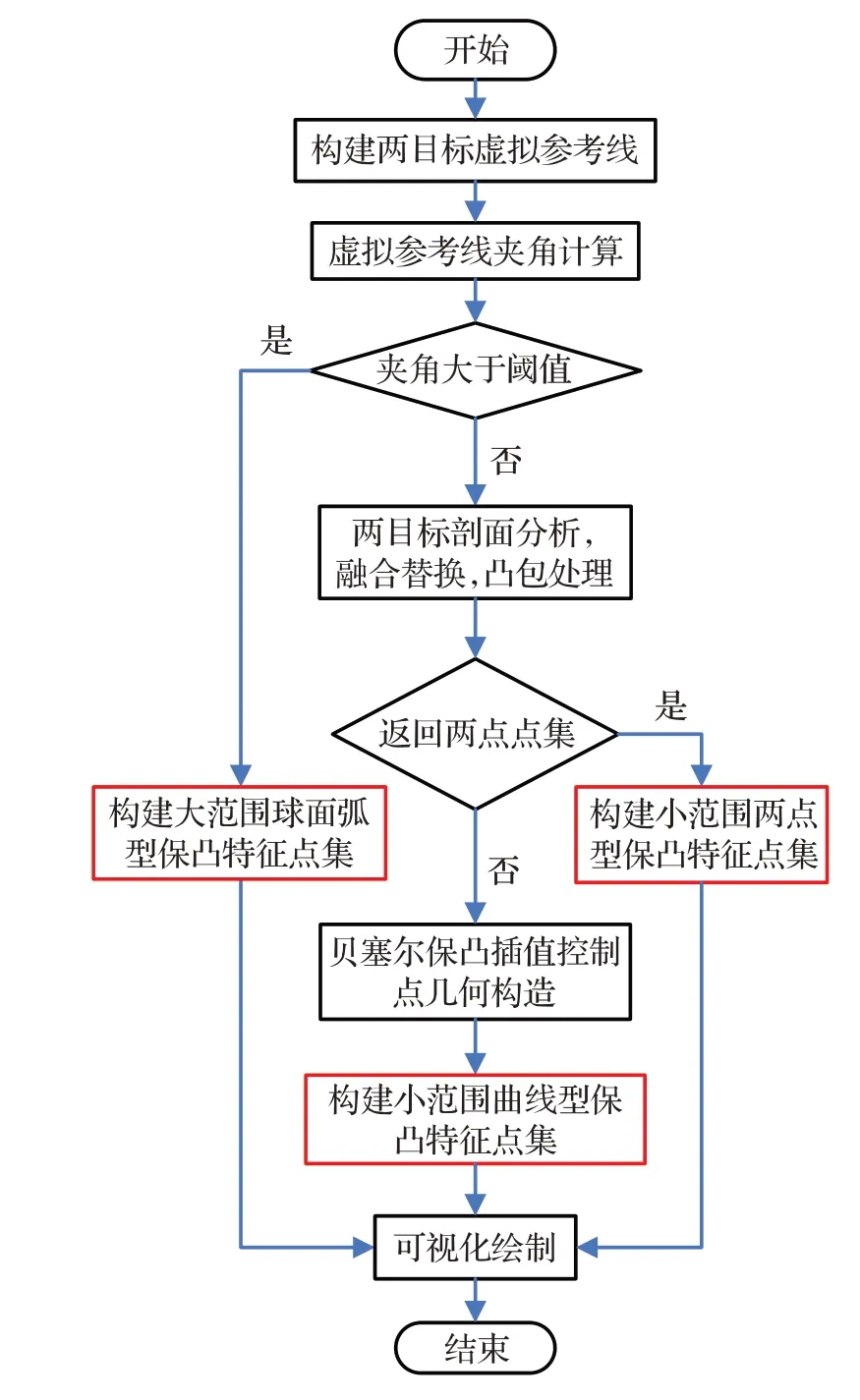
圖2 雙目標單一關系可視化流程圖

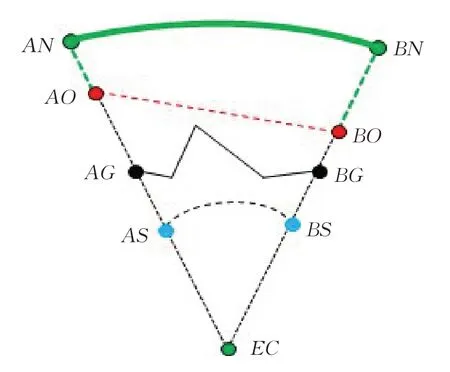
圖3 大范圍球面弧保凸特征點集示意圖

步驟3 構建大范圍球面弧型保凸特征點集（第III類保凸特征點集）。

沿線段ECAO 延伸至AN ；沿線段ECBO 延伸至BN 。點AN 與BN 的高度統一采用輸入參數：Height 。最后形成的折線段：AO 點、AN 與BN 之間的球面弧線各點、BO 點，構成保凸特征點集，即為目標AO 與目標BO 之間最終的連接曲線點集，參見圖3 中上部綠色折線上的點集。轉步驟8。

步驟4 兩目標剖面分析，獲取高程采樣。

使用高程采樣率參數Rate，采用GIS 兩點之間的剖面分析功能，沿球面插值采樣，計算目標AO 、目標BO 對應的經緯位置點之間的剖面高程點集，參見圖3中AG、BG 兩點及兩點之間黑色折線上的點。

步驟5 融合、替換、剔除及凸包處理。

采用目標點AO 替換點AG ；采用目標點BO 替換點BG ；基于點集：EC、AO、AO 與BO 之間的剖面點集、BO ，進行凸包（Graham 凸包算法）處理，得到凸包點集，再剔除點EC，形成新的凸點集。如果返回兩點點集，則轉到步驟6，否則轉到步驟7。

步驟6 構建小范圍兩點型保凸特征點集（第I類保凸特征點集）。

由AO 、BO 兩目標點之間連線與三維地形無交點，該兩點直接構成保凸特征點集（此處為統一描述，將線段兩點統一描述為保凸特征點集），線段AOBO 即為AO、BO 兩目標之間的連接線段。轉步驟8。

步驟7 構建小范圍曲線型保凸特征點集（第II類保凸特征點集）。

針對新的凸點集，采用逐段連續的光滑插值算法進行光滑處理[19]，獲得保凸特征點集，參見圖4 中AO 與BO 之間上部綠色曲線點集。轉步驟8。

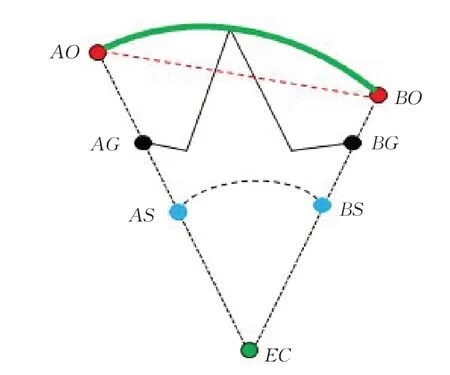
圖4 小范圍Bézier曲線保凸特征點集示意圖

步驟8 可視化繪制。

針對第I、II、III 各類保凸特征點集，采用幾何線段依次相連，基于VBO技術繪制出曲線，實現可視化。

2.4 算法補充

2.4.1 保凸可視化曲線（或點集）分類設計

算法產生的保凸特征點集共分為三種類型：小范圍兩點型（第I 類保凸特征點集）、小范圍曲線型（第II類保凸特征點集）、大范圍球面圓弧型（第III 類保凸特征點集）。

（1）小范圍兩點型（第I類保凸特征點集）

當在小范圍時，兩目標之間連線與三維地形無交點時，此時從視覺感知方面看，線段距離最短、最簡潔，因此此時采用兩點線段進行可視表達，視覺效果較好。

（2）小范圍曲線型（第II類保凸特征點集）

當在小范圍時，兩目標之間連線與三維地形有交點時，地面高山等的起伏影響將會占據視覺主導，所以此時要精細處理。獲得兩點之間球面弧上的高程采樣點集，獲取高程信息（地形起伏變化）；采用凸包算法，優選獲取地形的整體起伏趨勢；再經過保凸光滑插值處理，獲得保凸特征點集，最后生成的整條曲線基本擬合地勢、整體保凸等，視覺效果較好。

剖面分析中會使用對應金字塔級別的高程數據，GIS剖面分析接口中會設置相應的金字塔級別，算法中設置高程采樣率Rate 參數，主要也是考慮高程數據采樣級別影響，在實際中可根據實際對應調整該參數。

算法中曲線光滑采樣數參數Num，主要是調整曲線的光滑度，根據實際要求做調整。

（3）大范圍球面圓弧型（第III類保凸特征點集）

在較大范圍內，大球面弧線成為視覺感知的主體，尤其是在三維場景中，目標之間相距較遠時，視覺主體主要是兩者之間的連線關系，此時可主要考慮地球曲率的影響，忽略地表地形起伏的變化影響。同時也考慮：GIS 中的剖面分析，針對大范圍時，會存在一定的性能問題，所以針對大范圍情景，采用更高效、更簡潔的算法進行簡化處理，采用較粗略的地球球面弧繪制簡單，直接的球面插值采樣計算方面也更為簡單。算法中設置球面弧最大高度參數Height ，一般可設珠穆朗瑪峰高度8 848 m（或稍高些：10 000 m）。為保證在兩端處連接的光滑性，可進行局部中點逐次光滑逼近。較好的可采用基于視點的自動光滑，結合GPU 細分著色器進行實時光滑處理。

2.4.2 凸包算法前后的融合、替換及剔除策略設計

（1）采用目標AO 位置替換AG 位置；采用目標BO 位置替換BG 位置。即將目標位置點與剖面分析的高程點進行融合及替換。

設計思路：因為可視化是繪制目標AO 、目標BO的連接曲線，希望這兩點能是最終曲線上的首末點，所以將該兩目標點提前參與。特別注意：在本文中，為討論方便，限定軍事目標位置不能低于地面點以下，AO只能在AG 的外側（上部或該點），同理，BO 只能在BG 的外側（上部或該點）。

（2）凸包計算前，將地球中心點EC 加入，構建新點集：EC、AO、AO 與BO 之間的剖面點集、BO，基于該點集，采用凸包處理后，再從產生的點集中剔除地球中心點EC。

設計思路：點EC 參與凸包計算，主要是保證整個凸包點集向外凸出（從地球內部往外看），以便保證最后兩目標之間的連接曲線向外凸出（即向上凸出）；凸包處理后，再剔除地球中心點，主要是保證最后繪制的曲線起點與終點恰好是目標AO、BO 兩點。

經過上述策略處理，構建出的凸包點集，具有良好的整體外凸性，表現為特征點從地心向外分布，將地形高程采樣點集簡化為較少的保凸特征點集，優選出地勢的主體變化特征點，在一定程度上屏蔽地形的起伏[12-14]，為后面的可視化奠定了關鍵基礎。

2.4.3 保凸Bézier控制點的幾何構造

參照圖5，輸入凸點集ABCDE。以CD 為例：在該段上再插入兩個新控制點，然后以C、D 端點及這兩個新控制點，構造一段三次Bézier曲線。以下標表示新插入的控制點，例如：D 的左右兩側D1及D2。

（1）內部新增控制點的幾何構建過程

以點C 為例，在三角形BCD 中：

①計算中線GH 。

②記a=CG 與CH 的長度比值，在GH 上取點F，使得GF 與FH 的長度比值為：

a=CG/CH=GF/FH

③過C 點作GH 的平行線C1C2，使得CC1=GF，CC2=FH 。

④過C2作CD 的垂線L1；過D1作CD 的垂線L2，比較兩條垂線長度，取較小者（例如L2）對應的點D1，則過D1作CD 的平行線，交C1C2于點C3，則C3、D1即為CD 內部所求的兩個新控制點。

依據上述過程，依次逐個處理非端點的各點。在端點處，進行特殊處理：開始端點A 的右側控制點A2，使得A2=A，左側控制點A1忽略；結束端點E 的左側點E1，使得E1=E，右側控制點E2忽略。

（2）保凸Bézier曲線幾何設計思路

①四個控制點下的Bézier曲線形狀變化

參看圖6，在不同的控制點下，Bézier 曲線（中間曲線）形狀會有較大變化。圓形點表示開始與結束兩個控制點，中間方形點表示內部兩個控制點。可看出，如果Bézier 曲線需要保凸，則內部兩個控制點需要保證同側、不交錯，關鍵是保證四個控制點（特征多邊形）是凸點列[18-19]。

②整條Bézier曲線的連續保凸光滑

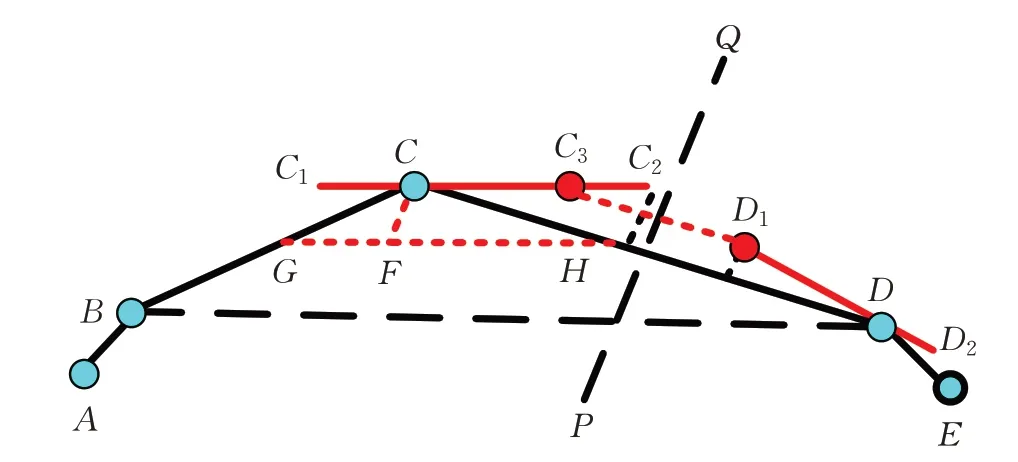
圖5 Bézier曲線保凸控制點構造示意圖

圖5 中，在線段AB 上，基于A、A2、B1、B 四個控制點，構造三次Bézier 曲線；在線段CD 上，基于C、C3、D1、D 四個控制點，構造三次Bézier 曲線，其余各段類似處理。將各段Bézier曲線依此相連，合成出整條的Bézier曲線，即為最終所求的曲線。整條曲線具有如下幾何特點：連續光滑；整體保凸。

圖6 內部控制點不同分布生成曲線示意圖

在每個輸入點的兩側生成的控制點共線，例如C 點的兩側控制點C1、C3，保證了各段Bézier 曲線在連接處的光滑[18]；輸入點列ABCDE 是凸點列，并且在每一小段上的Bézier新插入的兩個控制點處于同一外側（C點的兩側控制點C1、C3），四個控制點（C、C3、D1、D）組成的特征多邊形是梯形，保證了是凸點列，從而保證了該段上的Bézier曲線外凸[22]。綜合上述兩個階段的保凸處理，最后合成的整體Bézier曲線保凸[19-20]、連續光滑。

③兩個新控制點無交錯的證明

下面證明：在每個輸入點兩側插入的新控制點，長度小于所投影所在邊長的1/2。該處理主要是保證新插入的兩個控制點不會出現相互交錯，從而避免該小段上的Bézier曲線出現扭曲等現象，參見圖6（c）。

由構建過程知a=CG/CH=GF/FH，即GF=aFH，CG=aCH 。在三角形GCH 中，GH ＜GC+CH，GH=GF+FH，得出GF+FH ＜GC+CH，即有aFH+FH ＜aCH+CH，即FH ＜CH ，由構建過程知CC2=FH ，H是CD 中點，可知：CC2＜1/2CD。因為C3處于C、C2之間，所以CC3＜1/2CD，類似可證明DD1＜1/2CD，即C3與D1位于CD 的垂直平分線PQ 兩側。

④平行截取處理的保凸及視覺設計

“過D1作CD 的平行線，交C1C2于點C3”，使得C3D1∥CD，通過這種平行截斷，構建了一個梯形，保證了四個控制點組成的特征多邊形CC3D1D 是凸點列，由Bézier曲線的保凸性可知：特征多邊形是凸多邊形時Bézier曲線是凸的，而且較好地抑制了每小段（CD）上構建的Bézier曲線可能出現的單側較高凸起的現象[18]，延伸到空中的空間緊湊感也更好，曲線的局部對稱性也得到較大的改善。在C3D1與CD 之間，任意平行線與兩側的交點，都能滿足凸點列要求，但是與CD 太接近，導致該段上的Bézier曲線過度接近CD 線段，視覺上無法感覺出光滑的效果。也可不用平行線段，只將C2朝C1回移，找到保凸的新點，構成凸點列，但是中間兩個控制點的高度可能不同，曲線可能會出現單側凸起現象，曲線的對稱性會較差。綜合考慮，平行截取方法構建的Bézier曲線貼近凸包線、連續光滑、近似對稱、空間占有較少等，視覺上的美感較好。

2.4.4 算法時間復雜度分析

整個過程主要包含三個階段：剖面分析、凸包提取、Bézier插值光滑。剖面分析主要是依據高程網格數據，線性查詢出采樣點的高程數據，時間復雜度O(N)；Graham掃描算法時間復雜度為O(N×lb N)[17]；Bézier光滑處理時間復雜度為O(N)。整體時間復雜度為O(N×lb N)，其中N 為點集中點的個數。

2.4.5 視覺偏移調整量Modify參數

在三維疊加矢量顯示時會出現z-fighting 閃爍現象[8]，一般需要做一定的處理，保證無閃爍的視覺效果。在構造凸包點集前，針對高程采集的中間點可增加一定的視覺偏移量（兩個目標點不增加該偏移量，保證首末位置的準確性），進行適當升高，算法中的視覺偏移調整量Modify 主要是考慮此處，可根據實際進行調整。本文可視化算法中已保證整條曲線外凸，所以增加稍許偏移量，不會影響整條曲線的整體外凸趨勢，視覺效果上影響較小。

2.4.6 視覺美學原則的符合性分析

圖的繪制美學原則[4]主要包含直線邊原則、區域最小化原則、凸多邊形原則等，本文算法依據這些原則實現連線的繪制。

（1）直線邊原則

人類視覺感知最直接的方式，是最直觀的展示網絡連接的方式。在兩點之間不會穿山的時候，優先選用直線段繪制連線，即小范圍兩點型。

（2）區域最小化原則

網絡拓撲圖的繪制應該盡量節省屏幕空間。本文算法中小范圍曲線型依地勢進行繪制，大范圍球面圓弧型以珠穆朗瑪峰高度進行約束，與文獻[6]中的直接采用拋物線繪制相比，三維空間占用較少，屏幕占用空間也會較少。

（3）凸多邊形原則

與凹多邊形相比，凸多邊形具有視覺上的完美感，視覺美感較好。本文算法中小范圍曲線型由凸包和保凸的Bézier 插值得到，大范圍球面圓弧型擬合地球球面，整條曲線外凸，和球心可以構成完整的凸多邊形，并且由此能消除視覺上的抖動現象。

圖7 保凸特征點集不同類型的多重繪制示意圖

3 軍事目標群體多重關系的保凸可視化

針對軍事目標群體多重關系的可視化，可通過分解為兩目標之間單一關系的三維可視化進行處理。

3.1 可視化數據模型

基于圖論，建立數據模型M=(V,E)，V ：目標（或頂點）集合（含位置信息，顯示樣式：包圍球、顏色等）；E：關系（或邊）集合（含連線樣式：顏色、粗細、動態、方向性、繪制偏移量等基本顯示屬性）。

3.2 構建性能優化

目標群體包含的關系較多時，顯示連線的構建，整體來說計算量將會比較大。考慮到每條連線的構建過程相互獨立，可采用OpenMP或CUDA等高性能并行計算API[23]，進行性能優化。

3.3 顯示性能優化

繪制時可采用GPU Shader進行高性能等繪制[11]。

3.4 多重關系的偏移繪制

兩目標之間，如果存在多種關系時，需要考慮不同連線的偏移，避免兩目標之間不同連線的空間顯示重疊，需要符合圖的美學一般原則：邊交叉數量盡量少。針對三種保凸特征點集類型，進行不同的多重偏移處理：

（1）小范圍兩點型

作中垂線，在中垂線上向外（從地球球心向外看；如果線段垂直地面，可考慮以指北針方向為基準，增加旋轉偏移）取一點，采用最大值拋物線法或最大值Bézier曲線法構建，結果見圖7（a）中最上部的綠色及藍色曲線，可依次向外追加繪制偏移量向空中擴張。

（2）大范圍球面圓弧型

將兩線段分別向外旋轉一個繪制偏移角度，并分別延長一個繪制偏移長度，再整體繪制，參看圖7（b）中最上部的全部藍色折線部分。

（3）小范圍曲線型

將高程剖面分析中（不含兩個端點）各點高度增加一個繪制偏移量，再采用凸包擬合光滑法（簡稱：凸包擬合法）進一步處理，參見圖7（c）最上部的藍色弧線部分。

4 實驗

4.1 實驗條件

Win7 64位操作系統，i7-3770，3.4 GHz CPU，4 GB內存，GTX 650ti顯卡。三維開源圖形引擎Open Scene Graph（OSG）[24]版本為3.0.1。采用1∶25 萬DEM 高程數據，地理范圍：北京香山附近。

4.2 結果及分析

4.2.1 作戰態勢圖繪制效果

分別使用本文算法、貼地繪制和直線繪制一張作戰態勢圖，包含目標13個（其中空中目標2個，地面目標11個），連線20條，如圖8、圖9、圖10所示。

圖8 本文算法繪制效果

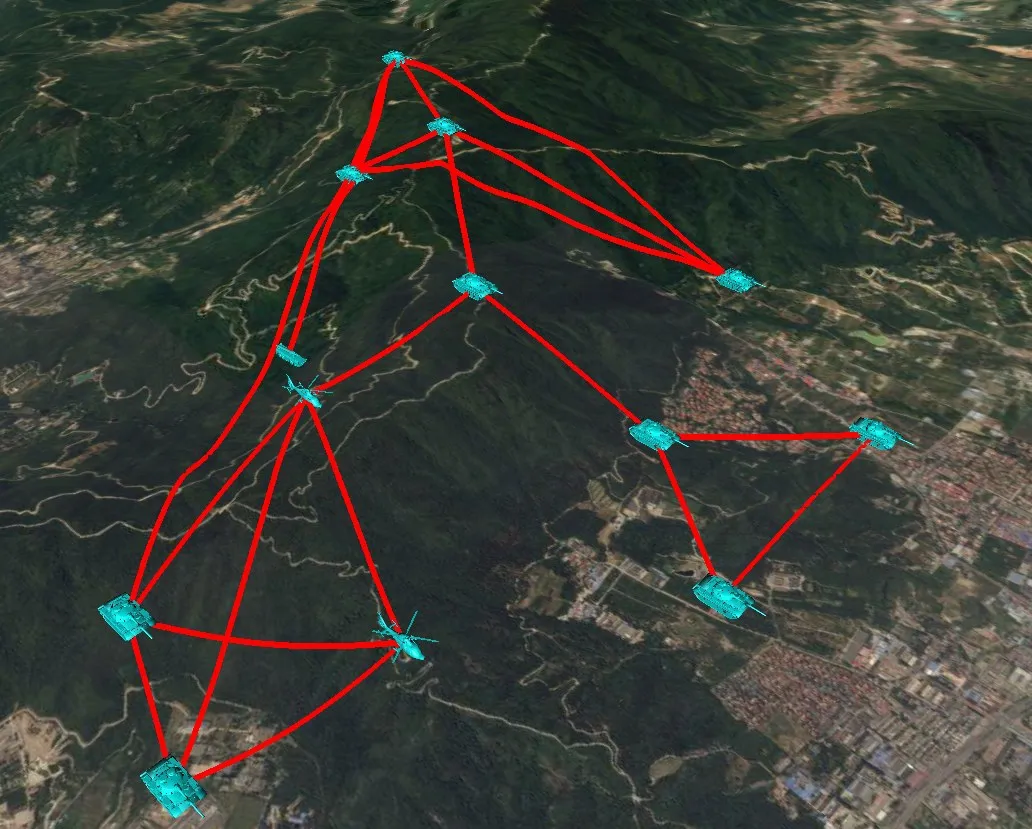
圖9 貼地繪制效果

比較圖8和圖9可看出：圖9中貼地連線，部分連線凹凸變化，出現視覺上的抖動感，其中5 條具有明顯抖動，2條有一定的彎曲，都是由于下方空中目標產生，共占比35%。產生抖動和扭曲的連線不符合圖的凸多邊形原則，視覺美感較差。圖8 中采用本文算法繪制，連線保證外凸（從球心方向往外看），符合圖的凸多邊形原則，視覺美感較好。

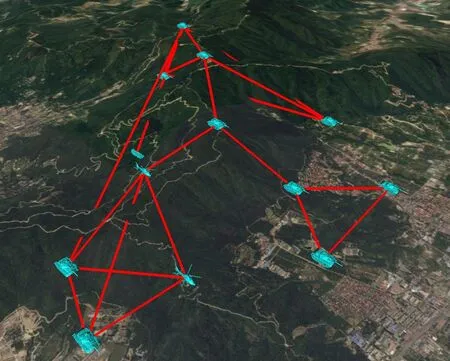
圖10 直線繪制效果

比較圖8 和圖10 可看出：圖10 中直線繪制，部分連線出現“穿山入地”現象，其中5 條比較明顯，1 條輕微被地形遮蓋，共占比30%。“穿山入地”導致連線在視覺上出現“破碎”感，視覺效果較差。圖8 中采用本文算法繪制，連線外凸，較好地對“穿山入地”的連線進行了校正，已基本沒有穿山入地現象，驗證了本文算法的有效性。

整體上看，本文算法繪制的效果，比貼地繪制和直線繪制的效果要好，綜合來看，該態勢圖中有7 條連線得到了改善，效果改善提升約為35%。

4.2.2 局部連線繪制效果與分析

圖11中高程采樣后，經過凸包處理，共有凸包點六個，其中右側除端點外還有兩個凸點。

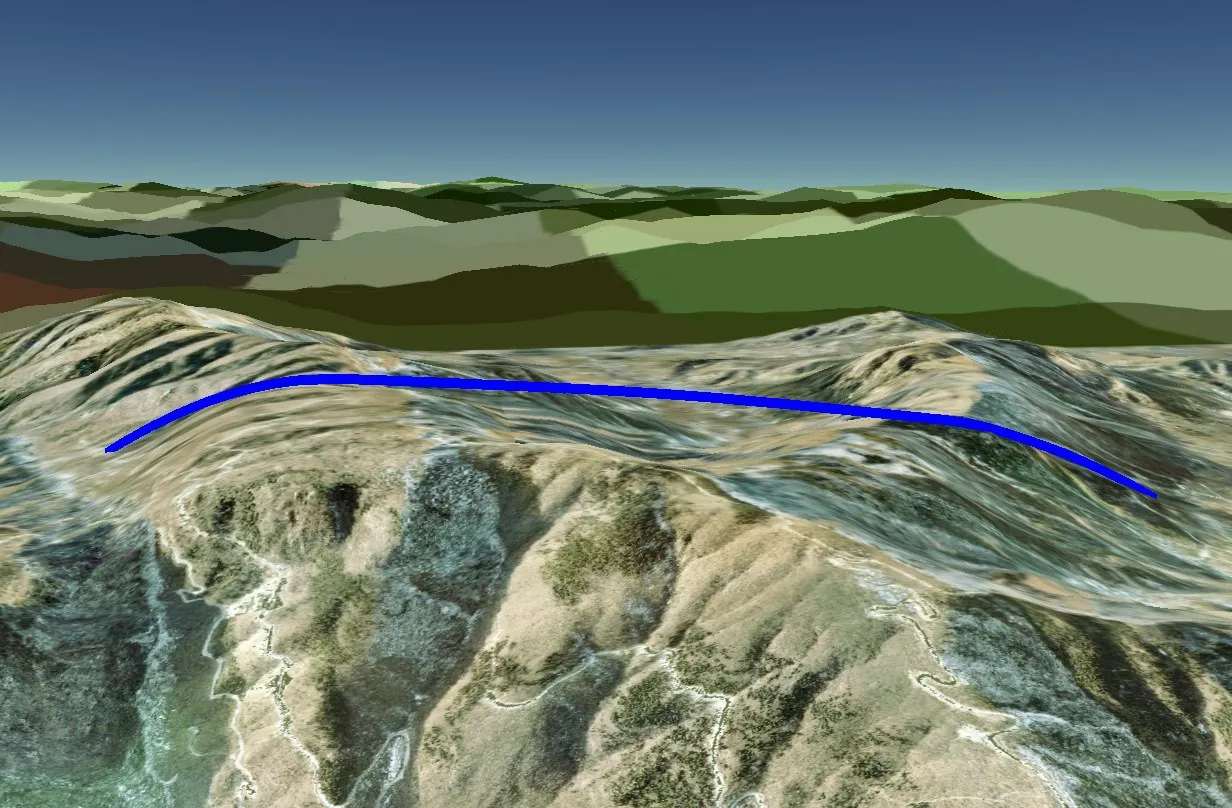
圖11 跨越多山峰：凸包擬合曲線效果

比較圖11～圖13，可看出：（1）凸包擬合曲線能提取多個山峰的主要趨勢，無“穿山”現象，保凸、光滑。（2）貼地曲線，每點取自實際的地面高程點，與凸包擬合曲線相比，視覺感知波動較大，不符合圖繪制美學中的凸多邊形原則；從不同的視點看，中間山坳部分的曲線可能會被附近的山引起前后遮擋，造成視覺上對整條曲線的“間斷感”及“破碎”感[12]，而凸包擬合曲線則有較好的抗“破碎”能力。（3）最大值Bézier 曲線使用首末凸包點及最高凸包點三點生成。只在最高點附近擬合較好，在右側較低山峰附近，與凸包擬合曲線在該處差距較大，因為只使用了左側的最高凸包點，缺失了中間右側的凸點，忽略了這些凸包點處的地形高度信息，導致擬合地勢不足，在較低處附近出現了部分曲線的“穿山”現象。

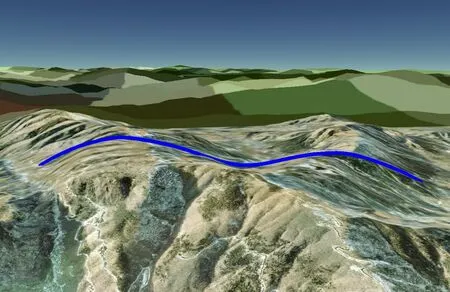
圖12 跨越多山峰：貼地曲線效果

圖13 跨越多山峰：最大值Bézier曲線效果

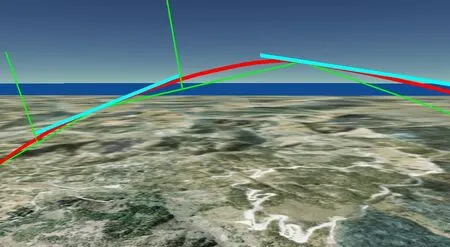
圖14 曲線局部幾何特征綜合分析（隱去高程后）

圖14中的下部細折線為凸包線，中間曲線為Bézier曲線，上部粗線段為控制點連線，向上的垂線為凸包邊的垂直平分線。從該圖可看出：（1）新插入的控制點在垂直平分線兩側，不會越界與交錯；（2）每一小段上的Bézier 曲線保凸且處于外側，與凸包線的凸性一致；（3）兩個新控制點連線與該段基本平行，特征多邊形構成凸點列；（4）每一小段上的Bézier曲線近似對稱，沒有明顯的單側凸出現象；（5）整條曲線（中間曲線）保凸，貼近凸包線，與文獻[6]中的拋物線效果相比，空間占用更少；（6）整條曲線連續、光滑。

4.2.3 算法性能與結果分析

對算法中的時間及中間數據進行統計，最大值Bézier 曲線（簡稱最大值曲線），凸包擬合光滑線（簡稱凸包擬合線）。表1 是繪制不同數目曲線的時間統計，表2是不同精度時各類曲線生成的時間統計，圖15是與之對應的曲線圖，表3是與表2對應的高程采樣點、凸包采樣點等的點數統計，圖16是與表3對應的高程采樣點數與凸包點數比較曲線圖。精度系數越大，高程采樣點數越多，曲線越精確，默認精度系數取0.1。

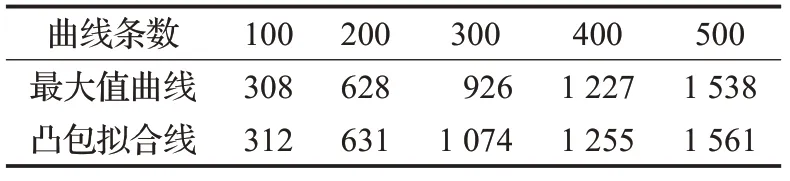
表1 不同數目曲線的生成時間 ms

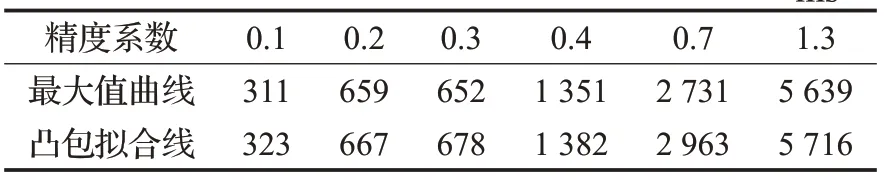
表2 不同精度曲線的生成時間 ms

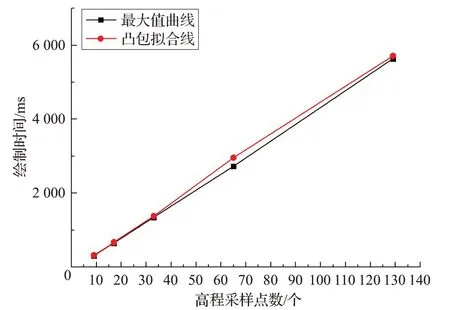
圖15 不同采樣點數生成時間

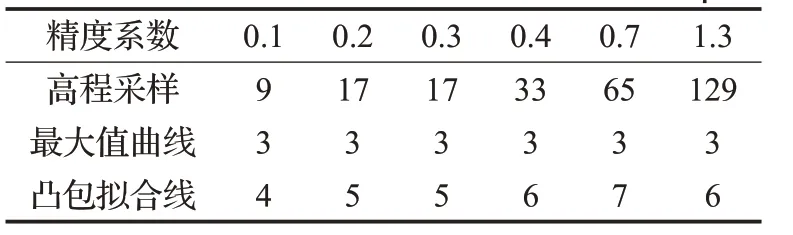
表3 不同精度曲線的點數 個

從表1 可知，隨著曲線條數的增加，凸包擬合線生成時間與最大值曲線生成時間都呈線性增長，兩者時間基本近似。

表2是不同精度下，凸包擬合線生成時間與最大值曲線生成時間都呈線性增長，兩者時間也基本接近。結合表3，參看圖15，可看出：隨高程采樣點數的增加（即精度增加），凸包擬合線生成時間與最大值曲線生成時間都呈線性增長。

從表3 看出，高程采樣點數變化范圍：9～129，而對應的凸包擬合線（光滑前）的凸包點數已得到極大的優化，點數范圍降低到：4～7。參看對應的圖16可知：在高程采樣點數不斷增加（即精度增加）的情況下，凸包點數基本趨于穩定，這表明了凸包在抽取地勢整體變化趨勢方面，具有很強的簡化能力。

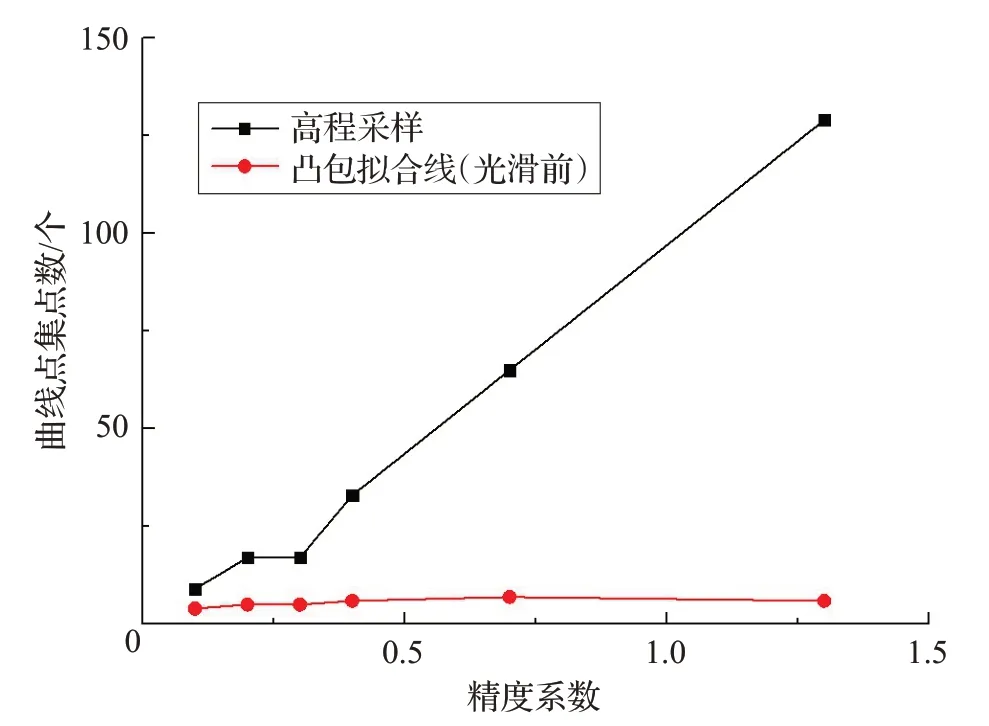
圖16 凸包點數和高程采集點數對比

4.3 實驗結論

綜合上述實驗結果，結論如下：保凸可視化算法生成的目標連接曲線具有較好的特點：整體保凸、光滑、擬合地勢較好、無“穿山入地”現象、符合圖的美學原則等。算法中的凸包對地勢整體變化趨勢的抽取具有較強的能力。

5 結束語

通過在目標之間進行剖面分析，獲得三維地勢的起伏變化信息；通過與目標位置等進行保凸融合，采用Graham 掃描算法，優選出了反映整體地勢變化趨勢的保凸特征點集；通過設計保凸的Bézier曲線控制點幾何構造方法，實現整條曲線的保凸光滑，而且整體空間占有較少。實驗結果顯示：目標連接曲線擬合地形變化整體趨勢，具有優良的保凸性，較好地保證了目標之間連接曲線的整體單凸性，整體單一向下彎曲，形成了空中分布的視覺感知，在一定程度上減弱了高山前后遮擋的影響，避免了視覺上的“S”型扭曲現象等，較好地消除了地形起伏引起的“穿山入地”，極大減輕了視覺感知上的間斷性“破碎”感[12]及抖動感等，視覺感知較好。

進一步：（1）研究STK、ECharts、FireEye等軟件中的動態特效及光照效果[11]，完善可視化動態效果。（2）針對網絡作戰領域，探索虛擬網絡空間與地理空間的混合顯示，深入研究地理因素約束下的網絡態勢可視化。（3）針對軍事中作戰編隊這種特殊群體，借鑒復雜網絡社區劃分的思想進行挖掘[25]，并進一步探索更好的群體關系可視化。（4）針對小范圍兩點型，可考慮采用邊集束[10]技術進一步改善效果等。（5）針對拓撲結構復雜混亂的問題，考慮地形約束，進行布局算法，從而減少邊交叉數量，提升視覺美感，需要下一步深入研究。