關于兩個單形頂點的距離、側面積及體積的不等式及其應用
陳士龍
(安徽廣播影視職業技術學院,安徽合肥230011)
0 引言與主要結果
關于歐氏空間En中單形的幾何不等式研究,近期取得了很多重要結果,文獻[1]收集了大量幾何不等式研究成果,其中十分重要又有趣的是涉及兩個單形的一類幾何不等式。1981年,楊路等[2]將涉及兩個三角形的著名Neuberg-Pedoe不等式推廣到兩個n維單形,建立了涉及兩個單形形式的n維Neuberg-Pedoe不等式。隨后,蘇化明[3]和LENG[4]建立了涉及兩個單形體積與棱長的n維Neuberg-Pedoe不等式。最近,冷崗松等[5]建立涉及兩個單形體積與側面積的n維Neuberg-Pedoe不等式,LI等[6]建立涉及兩個單形體積與其k維子單形k維體積的k-n型Neuberg-Pedoe不等式,WU 等[7]和LI 等[8]建立涉及兩個單形體積與中線的Neuberg-Pedoe不等式,YANG[9]和LENG 等[10]建立涉及兩個單形的另一些有趣的不等式。
本文中設歐氏空間En中兩個n維單形Ωn={A0,A1,…,An},Ω'n={A'0,A'1,…,A'n}的體積分別為V,V',側面fi={A0,…,Ai-1,Ai+1,…,An},f'i={A'0,…,A'i-1,A'i+1,…,A'n}的面 積分別為Fi,F'i(i=0,1,…,n),記最近WU 等[11]建立了涉及兩個單形頂點的距離、側面積與體積的2個重要不等式:
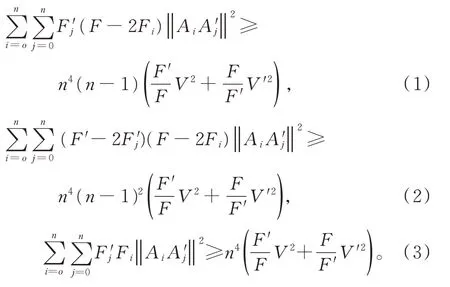
當Ωn與Ω'n皆為正則單形且它們的重心重合時,式(1)~(3)等號成立。楊世國等[12-13]研究了非歐空間中n維Neuberg-Pedoe不等式。
本文研究歐氏空間En中兩個單形頂點的距離、側面積及體積之間的幾何不等式問題,得到了幾個更一般的幾何不等式,此幾何不等式是式(1)~(3)的加強推廣和指數推廣。
對兩個n維單形Ωn與Ω'n,設
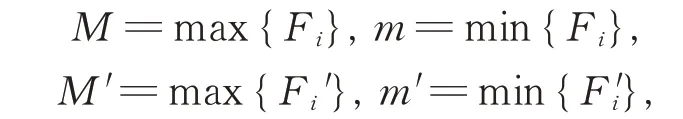
α,θ∈(0,1],記
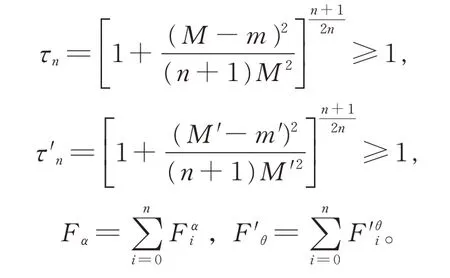
得到本文的主要結果:
定理1對En中兩個n維單形Ωn與Ω'n,α,θ∈(0,1],有
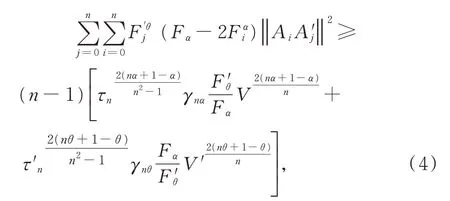

當Ωn與Ω'n為正則單形且它們的重心重合時,式(4)~(6)等號成立。其中,
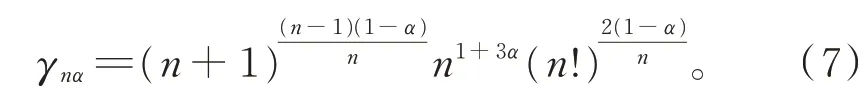
在定理1中,若令θ=α=1,便得到不等式(1)~(3)的加強推廣:
推論1對兩個n維單形Ωn與Ω'n,有
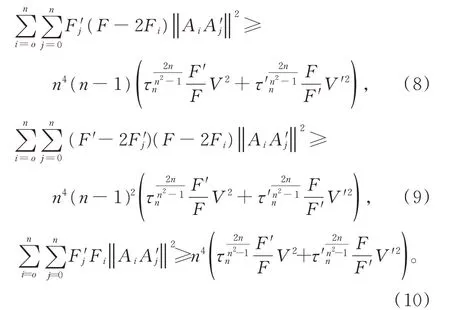
當Ωn與Ω'n為正則單形且它們的重心重合時,式(8)~(10)等號成立。
由于τn≥1,τ'n≥1,所以不等式(8)~(10)分別為不等式(1)~(3)的加強推廣。
由定理1可得不等式(1)~(3)的指數推廣:
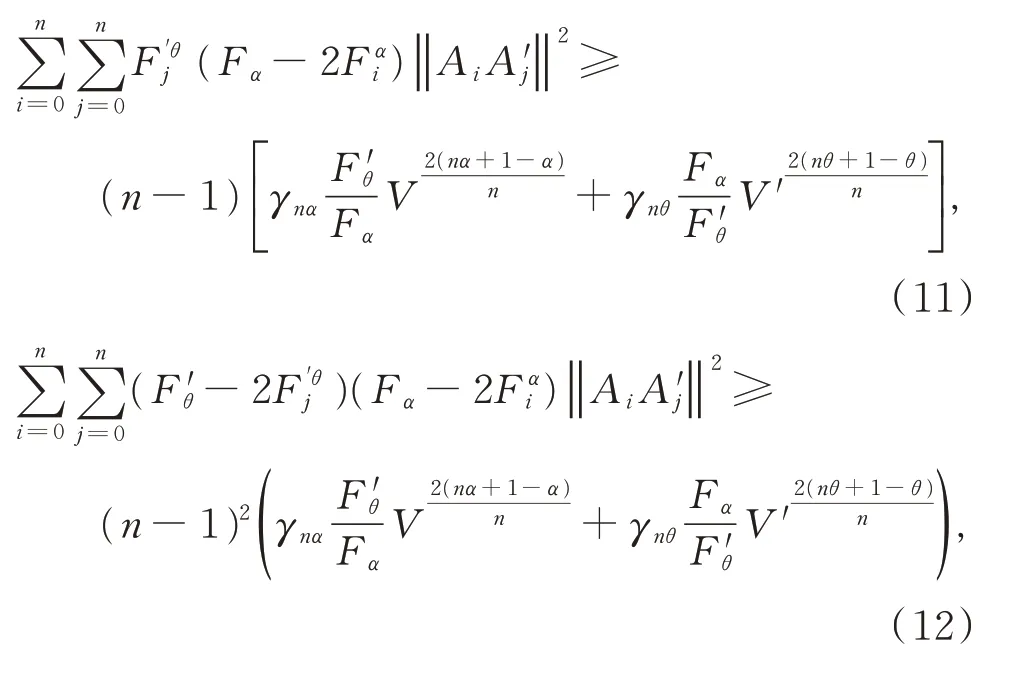
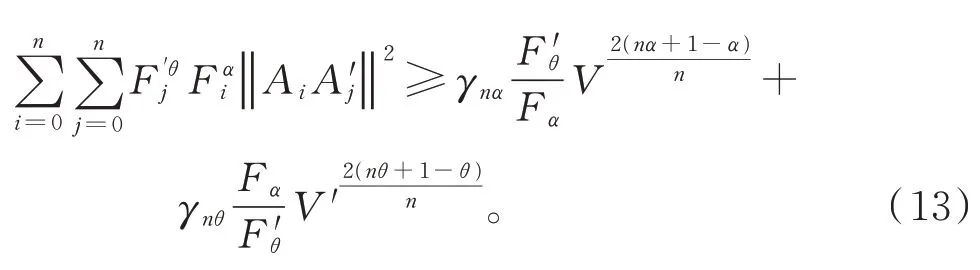
當Ωn與Ω'n為正則單形且它們的重心重合時,式(11)~(13)等號成立。
在不等式(11)~(13)中,若取α=θ=1,便得不等式(1)~(3)。
1 定理的證明
為證明定理1,需先證明以下引理。
引理1[11]設En中兩個n維單形Ωn與Ω'n的棱長分別為

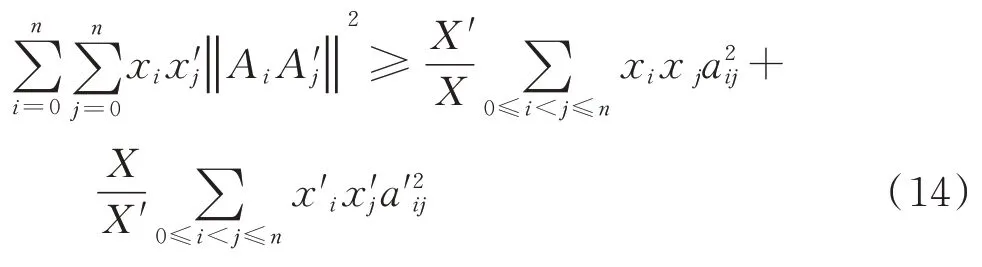
當且僅當質量組 {Ai(xi);i=0,1,…,n}與{A'i(x'i);i=0,1,…,n}的重心重合。
引理2對n維單形Ωn,有
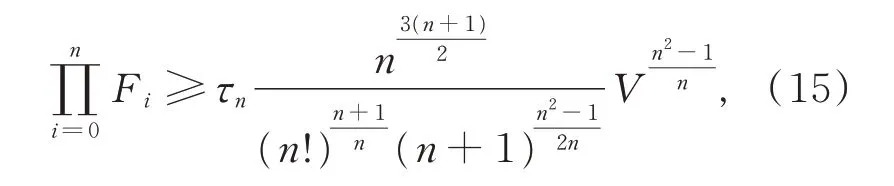
當Ωn為正則單形時等號成立。
證明設m個正數bi(i=1,2,…,m)的算術平均值為Am(xi),幾何平均值為Gm(xi),B=max {bi},b=min {bi},利用文獻[14]中的不等式

當b1=b2=…=bm時等號成立。
利用文獻[15]中的不等式
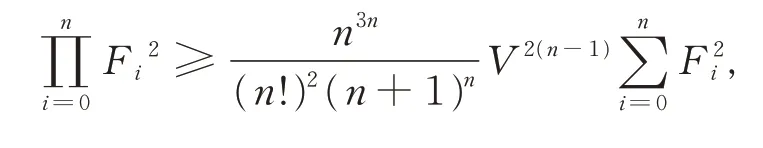
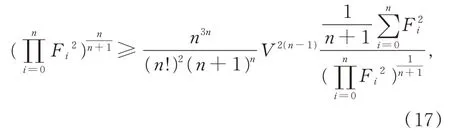
即當Ωn為正則單形時等號成立。
由不等式(16)、(17),便得不等式(15)。
引理3[5]設Ωn為n維單形,α∈(0,1],λi=則有

當F0=F1=…=Fn時等號成立。
引理4[15]設σN={Ai(mi);i=0,1,…,N}為En中的質點組(N≥n),mi>0(i=0,1,…,N),σN中任意k+1個點Ai0,Ai1,…,Aik所生成的k維單形的k維體積為Vi0i1…ik(0≤i0<…ik≤N),記
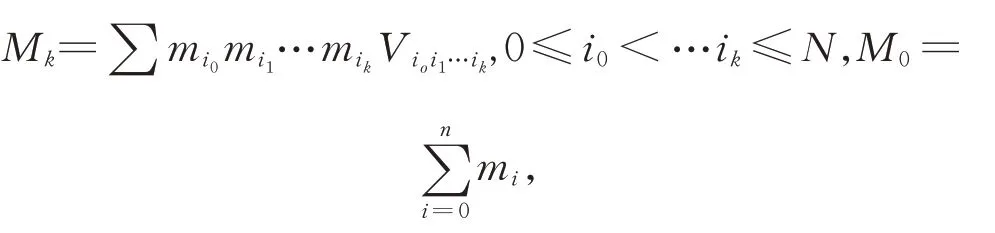
則有

當σN的慣量橢圓為一球時等號成立。
定理1的證明在引理1中,令xi=Fα-2Fi,x'i=Fθ i(i=0,1,…,n),由文獻[5]引理3的證明過程可知,xi>0(i=0,1,…,n),從而得
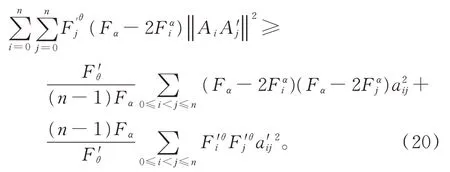
在引理4中,取N=n,k=1,l=n-1,此時σN是單形Ωn的頂點集,得
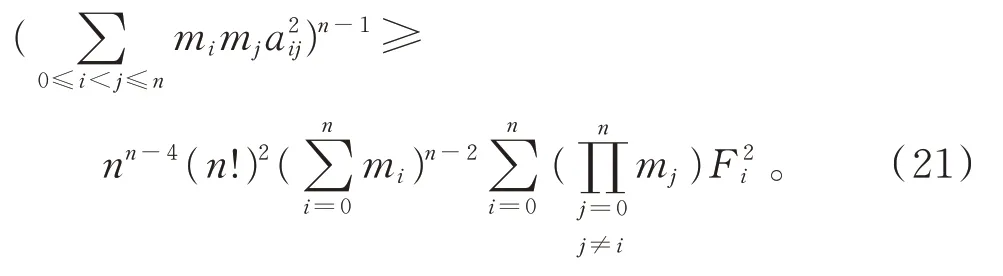
易驗證當Ωn為正則單形且m0=m1=…=mn時等號成立。
在式(21)中,令mi=Fα-2Fα i>0(i=0,1,…,n),得不妨設F0≥F1≥…≥Fn,從而有Fα0≥Fα1≥…≥

令ui=Fα-2Fα i(i=0,1,…,n),則有u0≤u1≤…≤un,從而有u-10F0≥u-11F1≥…≥u-1n Fn。
設λi(i=0,1,…,n)同引理3,利用Chebyshev不等式、不等式(18)及算術-幾何平均不等式,得到
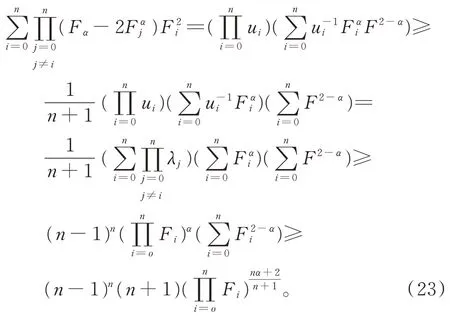
由算術-幾何平均不等式,有
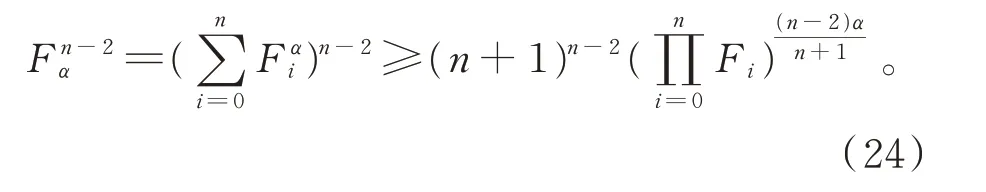
由式(20)~(24)得

由式(25)、(15)得
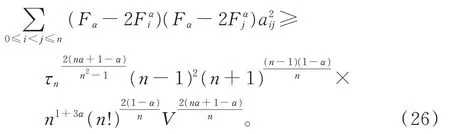
將不等式(21)應用于單形 Ω'n,并令mi=F'iθ(i=0,1,…,n),得
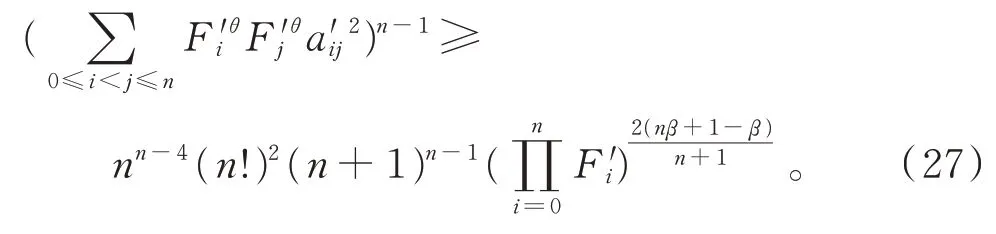
由式(27)、(15)得

由不等式(20)、(26)、(28),便可得不等式(4)。由證明過程易知,當Ωn與Ω'n為正則單形且它們的重心重合時,式(4)等號成立。
在不等式(14)中,取xi=Fα-2Fα i,x'=F'θ-再由不等式(26)便得不等式(5)。在不等式(14)中,取0,1,…,n),再由不等式(28)便得不等式(6)。
2 應 用
設K是En中的凸體,如果原點O∈intK,那么凸體K的極體定義為[14]
K*={x∈En/〈x,y〉≤1,y∈K}。由文獻[16]知,一個單形Ωn的極體也是一個單形Ω*n,Ω*
n稱為單形Ωn的極單形,且其 體積滿 足不等式
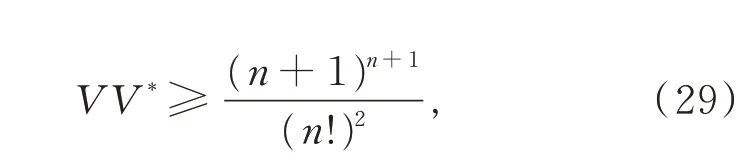
當且僅當Ωn的重心與原點重合時等號成立。
設n維單形Ωn的極單形Ω*n的頂點為A*i(i=0,1,…,n),頂點A*i所對的側面積為Fi*(i=0,1,…,n),記
對單形Ωn與Ω*n應用推論1、算術-幾何平均不等式及式(29),得
推論2設Ω*n為n維單形Ωn的極單形,則有

當Ωn為正則單形且其重心與O重合時,式(30)~(32)等號成立。
由于τn≥1,所以不等式(30)~(32)是文獻[11]中結果的加強推廣。
設單形Ωn的第i個旁切球半徑為ri,第i個側面上的高為hi,則有[1]
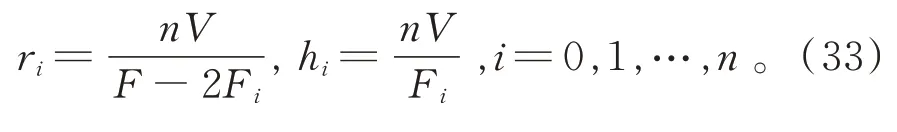
在推論1中,取Ωn與Ω'n為同一單形,并利用算術-幾何平均不等式和式(33),得
推論3對n維單形Ωn,有
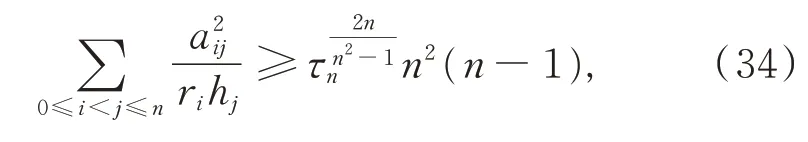

當Ωn為正則單形時等號成立。
顯然不等式(34)~(36)推廣了文獻[11]中相應的結果。

