一種求解線性碼最小距離的方法

（天津職業技術師范大學 理學院，天津 300222）

1 引言及預備知識

線性碼的最小距離與編碼的檢錯和糾錯能力息息相關，最小距離越大，檢錯和糾錯能力越強.線性碼的最小距離有多種求法，如利用權重分布多項式、窮舉、生成矩陣、校驗矩陣相關列、幾何學等方法求線性碼最小距離[1]237.多項式理論可以用來描述一部分具有良好性質的線性碼（如循環碼），且也可以通過編碼的方式將線性碼轉化為多項式，即用原數字信息與線性碼的生成矩陣做乘法，得到由多項式表示的線性碼一般表達式.在此基礎上，可以考慮由線性碼生成的理想It，其由線性碼的一般表達式中t個不同的多項式乘積生成，對于理想It，Gr?bner 基理論是用來解決理想生成元的一種手段.近年來，Gr?bner基在線性碼理論的研究中是一個活躍的研究領域，1992 年，Cooper 在文獻[2]中用多項式表示循環碼，進而用Gr?bner 基理論進行解碼，其是首位把Gr?bner 基應用到線性碼理論中的學者；文獻[3-6]應用Gr?bner基理論研究了線性碼的各種性質；文獻[7-9]對Gr?bner 基理論的應用做了詳細的介紹.

本文由文獻[1]中的一種求線性碼最小距離的方法展開，該方法主要運用代數方法求由線性碼生成的理想It何時有非零解，來確定線性碼的最小距離.但該方法的適用范圍有限，碼字較長時計算過程比較復雜，基于這種情形，提出一種新的方法——利用線性碼所生成理想的Gr?bner 基確定線性碼的最小距離.改進后的方法能夠處理原方法不能處理的一些問題，且會給出較好的結果.基于Maple 平臺對2種方法進行了對比，證明改進后的方法比原方法速度更快.

線性碼的本質是有限域上有限維向量空間的線性子空間，因此可以用線性代數中的一些工具對線性碼進行研究.記為有限域Fq上的n維線性空間.

自1965 年Buchberger 提出Gr?bner 基方法后，Gr?bner 基已經在各個研究領域得到了很好的應用，包括代數方程組的求解、多項式的因子分解、糾錯編碼中循環碼和代數幾何碼的譯碼、密碼學等研究領域.Gr?bner 基與單項式的序關系密切相關，常見的序關系有字典序、分次字典序、分次逆字典序等.

2 基于Gr?bner 基的最小距離算法

由命題1 可知，可以通過計算It的零點集來判定碼C的最小距離，但是當n和t較大時，利用此方法無法在有限時間內得到結果，實例驗證可以說明利用命題1 計算最小距離耗時更長.

直接計算理想It的零點集較為困難，但可以利用理想的Gr?bner 基求出其零點集，這是計算理想零點集的一個有效方法.

命題2 是對命題1 的改進，它給出一種求碼C最小距離的新方法，即利用多項式理想的Gr?bner 基算法求碼C的最小距離.

根據命題2 求碼C最小距離時的基本思路為：首先確定碼C的一般表達式和多項式運算規則，通過一個循環構造理想It，接下來調用Maple 中用于計算Gr?bner 基的函數包，計算理想It在字典序下的Gr?bner基，輸出It的Gr?bner 基G，由此可確定所給線性碼的最小距離.

求碼C最小距離的Maple 程序：

3 實例驗證

給出3個實例，用命題2 求解其最小距離，并在每個例題后給出用Gr?bner 基算法計算由碼C生成的理想所需要的時間.

解由生成矩陣G可以得到碼字的一般表達式c=(x1,x2,x3,x1+x2+x3,x1+αx2+α2x3,x1+α2x2+αx3),由α2+α+1=0可知，α3=1，α2=α+1.經過計算可得到I1，I2，I3，I4的Gr?bner基分別為

用Gr?bner 基算法計算由二元線性碼生成的理想I1，I2，I3，I4所需要的時間分別為0.031 200 2，0.093 600 6，0.249 601 6，0.249 601 6，0.109 200 7 s.

例2 設五元線性碼C的生成矩陣為，求該線性碼的最小距離.

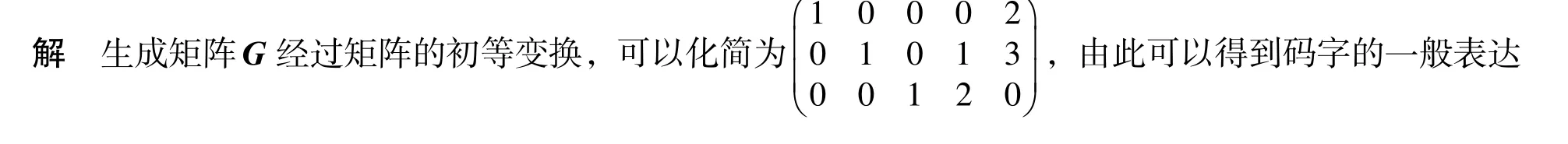
用Gr?bner 基算法計算由五元線性碼生成的理想I1，I2，I3所需要的時間分別為0.015 600 1，0.046 800 3，0.031 200 2 s.

用Gr?bner 基算法計算由碼C生成的理想I1，I2，I3，I4，I5，I6所需要的時間分別為0.062 400 4，0.483 603 1，5.990 438 4，42.276 271，137.421 280 9，195.999 656 4 s.

注在例3 中，若用命題1 來求解碼字的最小距離，首先要根據定義5 給出It（t=1,2,3,4,5,6），再計算It在F2中何時有非零解，從而得出二元碼C的最小距離.利用命題1 計算I1，I2，I3，I4，I5，I6零點集所需要的時間分別為0.24，0.82，9.85，70.42，200.82，285.67 s，所需時間明顯多于本文所給方法.因此，當碼長較長的情況下，用Gr?bner 基算法計算碼C的最小距離速度更快.

4 結語

最小距離反映了線性碼的檢錯和糾錯能力，因此研究線性碼最小距離的求解方法對線性碼的測評具有重要意義[11].本文介紹了基本的代數編碼知識，利用線性碼所生成理想的Gr?bner 基對原有線性碼最小距離求法進行改進，提出了一種求解線性碼最小距離的新方法，并用實例驗證在碼字較長的情況下，新方法比原有方法的計算速度更快.