基于柱殼法及柱坐標系求解旋轉體的體積

（信息工程大學 基礎部，河南 鄭州 450001）

在一元函數積分學中，微元法[1-3]是定積分的幾何應用[4-5]和物理應用的理論基礎.利用微元法可以求解旋轉體的體積，但是當曲線圍成的平面區域繞不同的坐標軸旋轉時[6]，積分變量和體積微元的選取方式可能大相徑庭，其中主要有柱片法和柱殼法2 種方式[7-8].在多元函數積分學中，也可以利用二重積分或三重積分求幾何體的體積，對于旋轉體而言，利用柱面坐標系[9-10]求解其體積計算過程非常簡便.本文從利用定積分中的柱殼法求解旋轉體的體積逐步過渡到利用三重積分在柱坐標系下計算旋轉體的體積，將2種情形下求解旋轉體的體積建立起聯系，以達到學生對柱坐標系更容易接受和理解的目的.

1 柱殼法求解旋轉體的體積

設函數y=f(x) ≥0,x=a,x=b及x軸圍成的平面區域繞y軸旋轉所得旋轉體的體積為V（見圖1）.

取x為積分變量，積分區間為[a,b]，任取小典型區間[x,x+dx]?[a,b]，相應于[x,x+dx]的窄曲邊梯形繞y軸旋轉所得立體的體積近似于以2πx為長，以f(x)為寬，以dx為高的長方體的體積，即體積元素為dV=2πxf(x)dx，將體積元素在[a,b]上作定積分，則得到旋轉體的體積.柱殼法是求解此類型旋轉體體積最常用的方法，其形式簡單，計算起來方便快捷.

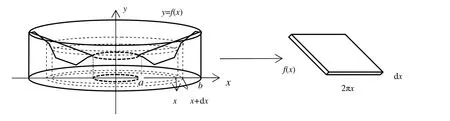
圖1 利用柱殼法求解平面區域繞y 軸旋轉得到的旋轉體的體積

當y=f(x) ≥ 0且在[a,b]上單調減少時，可類似討論.

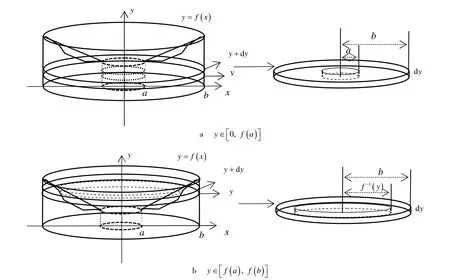
圖2 當y =f (x) ≥ 0且在[a ,b ]上單調增加時，以y 為積分變量分割旋轉體求其體積

討論當y=f(x) ≥ 0，但不是[a,b]上的單調函數時的情形.由于y=f(x)在[a,b]上不單調，因此可以通過求y=f(x)在[a,b]上的單調性發生變化的點將區間[a,b]分成若干單調區間，分別求取每個單調區間所對應的曲邊梯形繞y軸旋轉所得立體的體積，求和即得總旋轉體的體積.假設分點為x1,x2,L,xk-1，令x0=a,xk=b，若[xi,xi+1]是y=f(x)的單調增區間，由分析可知

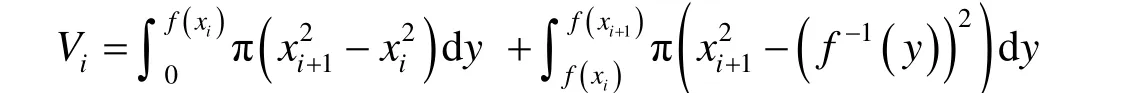
若[xi,xi+1]是y=f(x)的單調減區間，同理可得，因此整個旋轉體的體積為.至此，以y為積分變量求解旋轉體的體積問題便得到了解決.

至此，分別以x,y為積分變量，利用微元法解決了旋轉體體積的求解問題.有的學生自然會想到能否以另一種方式對旋轉體進行分割，即以過旋轉軸的平面將旋轉體分割成多個底面為扇環的曲頂柱體（見圖3）.但遺憾的是，即使兩張平面的夾角可以取很小，設為Δθ，此時由于x∈[a,b]，y=f(x)在[a,b]上的增量很大，不能找到一個體積微元來近似代替兩張平面截旋轉體所得的底面為扇環的曲頂柱體的體積.但如果繼續分割，添加以旋轉軸為軸的圓柱面和y為常數的水平面對此曲頂柱體進行分割，也即將3種分割方式結合在一起對旋轉體分割，切割出來的小扇環柱體體積的近似值就是柱坐標系下的體積微元（見圖4）.由此以平面極坐標中的極角為橫坐標，極徑為縱坐標，旋轉軸為豎坐標建立柱坐標系.

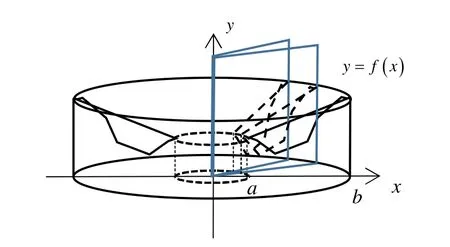
圖3 以旋轉角θ 為積分變量對旋轉體進行分割

圖4 以 r,θ,y為積分變量對旋轉體進行分割

2 柱坐標系下求解旋轉體的體積

在柱坐標系下，用3 組坐標面r=常數，θ=常數，y=常數分割旋轉體，把旋轉體分成若干個小立體，任取其中一個小立體，它的體積可近似看成以dr,rdθ,dy為長、寬、高的立方體的體積，因此旋轉體的體積微元dv=rdrdθdy.曲線y=f(x)繞y軸旋轉而成的旋轉面方程為，在柱坐標系下也即是y=f(±r)，記旋轉體所占空間區域為Ω，則利用直角坐標系下三重積分計算中的“先一后二”法可得旋轉體的體積為.

在對旋轉體的不同分割下如何求體積的思考中，引出了利用柱坐標求解旋轉體體積的方法.隨著問題的逐步推進，從柱殼法到柱坐標系，實現了一元函數定積分求解旋轉體體積到重積分求解立體體積方法的跳躍，既解答了學生在定積分應用中求旋轉體的體積時產生的疑問，又給了柱坐標系一個較為自然的引入.這種拓展有利于開闊學生的思維，幫助學生建立前后知識間的深層鏈接.