非參數統計的簡單應用
(廣東財經大學 廣東 廣州 510320)
一、對于非參數統計的心得
以往的所有課程中,對于參數統計我們有著詳細的方法去估計,參數估計,假設檢驗,大樣本正態分布,計算它的一系列樣本參數來推斷信息。例如,我們首先假設收入是服從正態分布的,于是我們就去計算樣本的期望、方差、峰度等來以此此來刻畫這一數據,再通過這些收集到的數據去做推斷。但是現實中的統計工作我們是不知道怎么分布情況的,不是t檢驗,方差分析也做不了,線性回歸也不行,時間序列分析等等都不行,簡單來說,我們對于分布一無所知,甚至數據是殘缺的,不完整的,這時候我們就只能用非參數統計方法去處理這些處理不了的問題。常用的非參數統計方法有:符號檢驗,Wilcoxon秩和檢驗。
二、方法介紹
(一)符號檢驗
符號檢驗是最基本的非參數統計方法,獲取到樣本X1,…Xn之后,不知道這是不是正態分布,因而就用不了t檢驗。在非參數檢驗里,用符號檢驗要熟知分位點以及廣義的分位點性質意義。簡單的二項分布,與分位點結合就形成了符號檢驗。對于符號二字的理解呢,則是這樣定義的:
檢驗原假設是H0:Qπ=q0(Qπ是針對連續變量的π分位點)
備擇假設則可以是大于也可以是小于,或者是不等,隨統計問題的具體而定。
假設都已經做好的,樣本收集過來,記大于樣本的點數為N+,小于的則記為N-,用小寫的n+和n-代表對應的實現值。n=n++ n-。如果此時零假設是成立的,則應該有n-與n之比約為π,或者說n-是大約nπ。于是這樣就得到了,在零假設成立的情況下,N-是服從二項分布Bin(n,π)的(要么是大于,要么是小于,于是是二項分布)。這里的符號意思N+就是樣本中所有減去q0之后的,這個差值還是為正的個數,同理,負號就是差值為負值的個數。更加深入一點可以構建卡方統計量:(|n_+-n_- |-1)2/(n++n-) 。這就是符號檢驗,不需要知道分布,只需要計算所謂的“符號”即可了,是非參數統計中最基本的一個方法。
(二)Wilcoxon秩和檢驗
用于多組數據的比較,對樣本數據進行統一的編秩,求出備組秩和,再以各組秩和的平方與例子推算的比值求得的總和來計算z值,類似的,在符號檢驗基礎上更加利用信息,減去要檢驗的數值,得到差值,再對其取絕對值,再排序,求秩(相同的取一樣的秩),令W+為差值為正的秩和,W-為差值為負的秩和。再去計算p值或者查詢臨界值。比符號檢驗更加高明的是利用到了差值多少的信息,符號檢驗只區分了正負,秩和檢驗可以理解為對不同距離的差值賦予了不同的權數。
三、非參數估計的優點總結
1.減少模型誤差是必然的,用到了更多樣本中的信息,傳統的參數發放就是基于分布的假定上,然而實際統計工作往往是滿足不了這些分布形式的,導致傳統模型與現實相背離產生模型上的偏差。而非參數估計的則是完全更多的,盡可能的去利用樣本數據的信息,不需要總體分布強加條件。可以去選擇與數據匹配的模型,而不是摁死了模型去讓數據削足適履,具有較好的穩健性。
2.適用范圍廣。從數據的角度來看的話,可以處理定距、定比數據,也可以處理定類、定序數據。而實際上呢,定類和定序則是大量存在社會科學和計算機科學領域的,應用范圍更加廣。從模型角度來看,假定條件沒有那么苛刻,適用范圍更加廣闊。
3.簡單易操作。秩在非參數統計來說是最關鍵的一個東西,我們在不知道樣本分布情況下,秩就是唯一我們能夠依靠從樣本里面提取出來的信息,從小到大排列,也非常易于理解。
四、秩和檢驗人口政策目標
十二大國家制定的控制人口目標是本實際末人口總量不超過12個億,雖然已經在很早的計劃生育國策下,人口還是增長,為此,我們需要做出預測趨勢是否會達到人口目標。其《綱要》指出人口的自然增長率控制在12.5%以內,可以用Wilcoxon秩和檢驗。
注:數據來源國家統計局(人口資料).中國統計年鑒.
基于兩個假設:1)總體分布連續 2)總體是對其中位數是對稱的
zi=|xi-q0|,自然的,q0是目標值,對z做秩和檢驗。在這里以正秩和檢驗統計量。
H0:人口自然增長率為12.5% H1:人口自然增長率小于12.5%
檢驗結果,這是1978年到1989年的
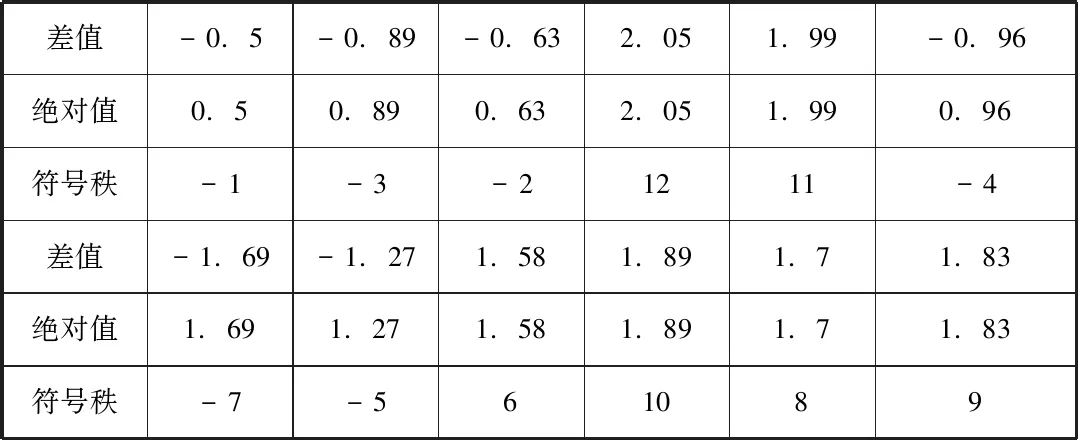
差值-0.5-0.89-0.632.051.99-0.96絕對值0.50.890.632.051.990.96符號秩-1-3-21211-4差值-1.69-1.271.581.891.71.83絕對值1.691.271.581.891.71.83符號秩-7-561089
正秩和為56,當n12時候,取顯著性水平為0.005時候,查表得知道臨界值為17,故拒絕原假設。不認為由足夠的證據證明可以控制人口自然增長率可以控制在12.5%之內,人口目標需要重新調整,人口政策需要重新規劃。
五、小結
非參數統計方法與參數統計很大不同就是假定的基礎不一樣,或者說條件更加的寬松,參數化更加的書本化,非參數統計在實際統計工作往往用的比參數統計多太多了。但是兩者的核心思想是一樣的,做出檢驗統計量去進行檢驗。這是至關重要的,兩者的長短處不同,應用范圍也是不同的。在解決不知道總體分布情況下,對總體信息知道的不是非常明確條件下,非參數統計無疑是好過參數統計的。

