基于物理的霧凇生長模擬算法

李 曄 ， 楊 猛 ， 上官大堰 ， 楊 剛

(1. 北京林業(yè)大學(xué)信息學(xué)院，北京 100083；2. 北京林業(yè)大學(xué)藝術(shù)設(shè)計學(xué)院，北京 100083)

霧凇是在低氣溫下，由空氣中尚未凝華的水蒸氣在樹枝等物體上不斷積累凍結(jié)粘連的結(jié)果。我國的一些地區(qū)由于其獨特的氣候特征以及地勢地貌，每年都會形成霧凇這種獨具風(fēng)韻的景觀，同時這些地區(qū)也是氣象部門重點關(guān)注的對象，因為在特定情況下，長時間的霧凇天氣會導(dǎo)致樹木、高壓線等被附著物積冰[1]，從而引發(fā)災(zāi)害事故，嚴(yán)重時可危害人民的生命財產(chǎn)安全。

自然界中的霧凇主要分軟淞和硬淞2種。軟凇結(jié)構(gòu)松散，稍受振動就會脫落，密度小，形狀類似于冰晶，是一種特殊的自然景觀，如圖1(a)和(b)所示；硬凇是空氣中的霧滴隨疾風(fēng)移動，遇到物體迅速凍結(jié)粘連的結(jié)果，形成速度很快，結(jié)構(gòu)緊湊、密度大、排列整齊，如圖 1(c)和(d)所示。

圖1 自然界中的軟凇和硬凇圖

霧凇的外觀、外形極其不規(guī)則，沒有均勻的表面且隨著生長時間變化，最主要的是在周圍環(huán)境發(fā)生變化時，其呈現(xiàn)的狀態(tài)各異，具有極高的隨機性。因而利用計算機圖形學(xué)生成場景時，巨大的計算量往往會成為實時顯示場景的瓶頸。

受WITTEN和SANPER[2]提出的擴散限制凝聚(diffusion limited aggregation，DLA)模擬金屬粒子聚集方法啟發(fā)，本文使用DLA的方式對軟凇的形成形態(tài)進行模擬，并考慮了風(fēng)力對于粒子凝聚產(chǎn)生的影響；同時在風(fēng)環(huán)境中，通過對霧凇生長過程中的受力分析，使用分節(jié)計算生長終點的方式對硬凇的形態(tài)進行模擬。

本文提出了一種基于物理的霧凇生長動態(tài)模擬算法，通過引入覆冰模型、材料力學(xué)模型、風(fēng)場、DLA方法，模擬風(fēng)環(huán)境條件下的軟凇和硬凇，特別是其生長方向和形態(tài)。

1 相關(guān)工作

1.1 冰凝結(jié)模擬

最早對晶體凝結(jié)過程進行模擬的方法是由KHARITONSKY和GONCZAROWSKI[3]提出的一種簡單的冰柱形成方法，雖然模擬方式十分簡便，計算速度也非常快，但并未達到真實的效果。

DLA是一種非常受歡迎的晶體生長方法，最初是文獻[2]為了模擬金屬顆粒的聚集而開發(fā)的，但該算法也被推廣到許多其他自然現(xiàn)象的建模，包括雪花生長等[4-5]。張倩等[6]通過觀察液體在固體冷表面上逐漸凝結(jié)生長的過程和特點，在原始分形理論的基礎(chǔ)上，提出了雙分支樹狀DLA模型，同時考慮冰晶表面在凝結(jié)過程中的散熱量，模擬出了固體冷表面的霜晶凝結(jié)過程隨時間變化的細(xì)節(jié)，并取得了極佳的效果。但是該方法并未考慮風(fēng)條件對冰晶形態(tài)產(chǎn)生的影響，而是在相對理想的條件下對冰晶進行生長模擬。

除了DLA方法，相場方法也是一種常用的晶體生長的方法。KOBAYASHI[7]以文獻[8]為基礎(chǔ)對物理學(xué)中的凝結(jié)方向進行了研究，首次成功地將相場應(yīng)用于雪花的生長過程的模擬中，并取得了十分真實的效果。除了相場方式之外，水平集方法在模擬晶狀結(jié)構(gòu)[9]方面也取得了成功，并且可實現(xiàn)更高的數(shù)值精度，但代價就是受限的計算速度。

文獻[10]提出了一種基于物理的模擬冰晶凝結(jié)的新算法，結(jié)合 DLA、相場方法和穩(wěn)定的流體解算器來控制冰的生長方向和形態(tài)，其得到的效果非常真實但是計算速度受到了一定的限制。隨之又在前面工作之上，引入一個額外的自由度，即方向場，并由溫度場和相場共同控制[11]，從而實現(xiàn)晶體模擬，利用高斯卷積加速計算，最后達到了十分真實的效果，但實現(xiàn)過程相對復(fù)雜。本文利用 DLA的方法模擬軟凇形成，其類似于大氣粒子凝結(jié)的現(xiàn)象，并考慮風(fēng)力對霧凇形成造成的影響。

1.2 風(fēng)場模擬

風(fēng)在自然景物模擬中扮演著十分重要的角色，如風(fēng)作用下樹枝的擺動動畫模擬、樹葉飄落模擬、海面隨風(fēng)波動模擬等等，都需要對當(dāng)前環(huán)境中的風(fēng)進行模擬。目前已經(jīng)提出很多關(guān)于風(fēng)的模型，如空氣動力學(xué)模型[12]、基于物理的風(fēng)力模型[13]等。羅勝華[14]在空氣動力學(xué)的基礎(chǔ)之上，通過風(fēng)速來計算作用在物體上的風(fēng)力，并引入噪音技術(shù)體現(xiàn)風(fēng)的動態(tài)效果，同時模擬風(fēng)條件下樹木的運動效果，但該方法對于具有非常復(fù)雜結(jié)構(gòu)的樹木模型時，計算速度是瓶頸。本文參考文獻[15]的方法，利用柏林噪聲函數(shù)來模擬風(fēng)場，模擬速度很快，且能很好地體現(xiàn)自然界中風(fēng)的隨機性，但缺點是會產(chǎn)生連續(xù)時間段內(nèi)風(fēng)的變化非常劇烈或基本未變化的情況而導(dǎo)致結(jié)果出現(xiàn)不自然的現(xiàn)象。因此本研究在柏林噪聲函數(shù)的基礎(chǔ)之上增加了平滑函數(shù)，既能快速地模擬風(fēng)場，又能在一定程度上減少出現(xiàn)劇烈變化或變化不明顯的不自然現(xiàn)象。

2 本文算法

霧凇是氣溫低于-2℃時，霧中無數(shù)的霧滴逐漸凝結(jié)而成，而在風(fēng)的影響下會產(chǎn)生軟凇和硬凇2種不同的霧凇。軟凇在風(fēng)力較為平緩的情況下，薄霧中的小水滴粘附到物體的外表面時形成；硬凇是在風(fēng)速較高的環(huán)境下，形成于樹枝或其他固體的迎風(fēng)面。

本文算法流程如圖2所示。算法開始于對用戶設(shè)定的當(dāng)前模擬溫度和風(fēng)速的判定，若溫度T大于等于T′ (實驗中T′取-2℃)，則不滿足生長霧凇的條件，系統(tǒng)提示用戶是否重新輸入溫度；若溫度小于T′，則滿足霧凇生長的溫度條件，根據(jù)溫度、空氣濕度、風(fēng)速等條件計算霧凇的生長點D以及生長長度Lw。然后根據(jù)風(fēng)速判斷霧凇種類，若風(fēng)速V小于等于V′ (V′=5.4 m/s)，則為軟凇，可利用DLA方法模擬其形態(tài)；若風(fēng)速V大于V′，則為硬凇，利用分節(jié)計算生長終點的方法模擬其形態(tài)，通過對每一節(jié)硬凇進行受力分析求出下一節(jié)硬凇。

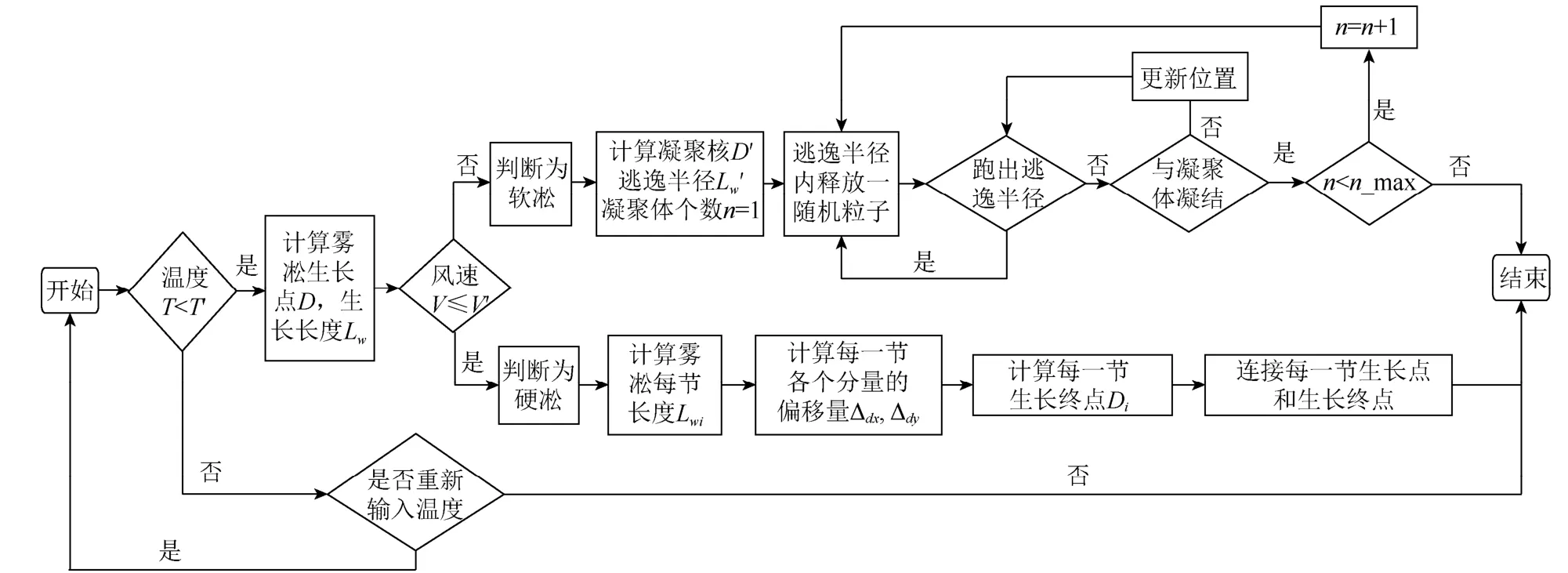
圖2 霧凇模擬算法流程圖

計算機中數(shù)據(jù)的表述均是離散的，將樹木模型上霧凇的生長離散化為在具有Mesh結(jié)構(gòu)(點、線、面等)表示的樹木幾何面片上生長，假設(shè)某一個三角面片上有若干生長點，每個生長點上都對應(yīng)著不同的霧凇長度、生長方向和霧凇形態(tài)。

如圖3所示，ΔABC是導(dǎo)入樹枝幾何模型上的某一個三角面片，點D，Dn1，Dn2，Dn3，Dn4是當(dāng)前三角面片上的生長點；向量e是生長點D上對應(yīng)霧凇的生長方向；單枝長度為Lw；向量n是三角形面片ΔABC的法向；風(fēng)向為向量Φ；風(fēng)速為V。

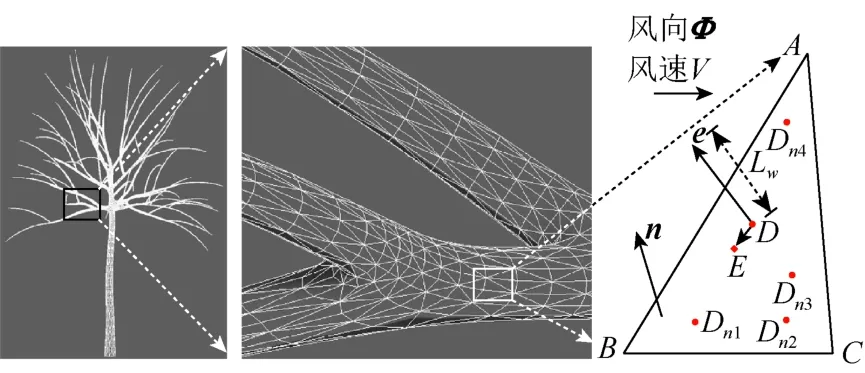
圖3 模型三角面片示意圖

2.1 霧凇生長點

通過導(dǎo)入樹木模型，本文在模型三角面片表面進行霧凇生長，并通過隨機取點的方式得到霧凇的生長點。每個三角面片上生長點的個數(shù)由三角面片的法向與風(fēng)向的夾角決定，夾角越接近于零，說明風(fēng)向與三角面片近似垂直，則與霧滴發(fā)生碰撞凝結(jié)的可能性大，此時生長點數(shù)量多，反之生長點數(shù)量少。如圖 3所示，計算每個三角面片上生長點數(shù)量，即

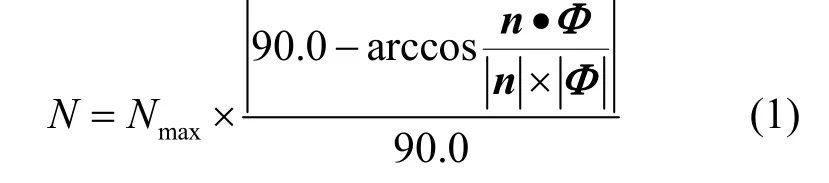
其中，n為三角面片的法向；Φ為風(fēng)向；Nmax為三角面片最大生長點數(shù)，本文在軟凇、硬凇模擬時Nmax分別取5和10。

2.2 霧凇生長長度

霧凇的生長長度與風(fēng)速、凍結(jié)系數(shù)、被附著物的橫截面積、生長時間等有關(guān)，因此本文引入覆冰模型來計算霧凇[16]的長度，即

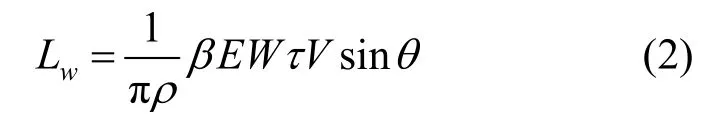
其中，Lw為霧凇的長度；ρ為覆冰密度并可以由公式得到，T為溫度。由于霧凇屬于干增長的過程，因此凍結(jié)系數(shù)β取值為1.0；W為空氣濕度，本文取值0.5；τ為霧凇的形成時間；V為風(fēng)速；θ為霧凇生長方向與水平方向的夾角；捕獲系數(shù)E為被附著物的橫截面積與覆冰后的橫截面積之比，反映了空氣中霧滴的聚集效率。

2.3 風(fēng)場模擬

自然界中的風(fēng)可以由風(fēng)速和風(fēng)向2個量表示，且均具有不均勻性和隨機性，而柏林噪聲能夠很好地模擬自然界中存在的一些隨機性。本文中的風(fēng)場在柏林噪聲的基礎(chǔ)上，增加了平滑函數(shù)使得模擬的結(jié)果更加自然，其采用的柏林噪聲函數(shù)為

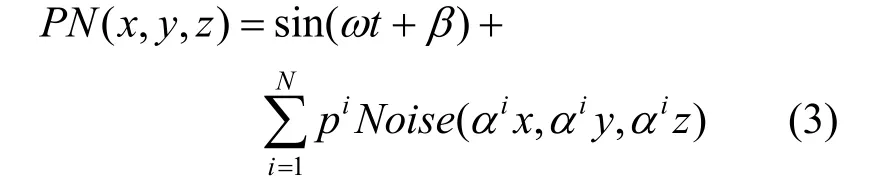
其中，p為振幅；α為頻率；N為倍頻；x，y，z分別為計算柏林噪聲點的坐標(biāo)；sin(ωt+)β為平滑函數(shù)；t為生成時間；Noise函數(shù)可平滑、插值隨機數(shù)生成器生成的隨機數(shù)。本研究選擇相對變化不劇烈的風(fēng)，因此采用大幅度低倍頻，p取2，α取0.5，N取 4。Noise函數(shù)是創(chuàng)建的隨機數(shù)生成器，其在(-0.5，0.5)之間生成隨機數(shù)，根據(jù)輸入的參數(shù)，可輸出基于當(dāng)前參數(shù)的隨機數(shù)，如果再次輸入的參數(shù)與之前的某一個參數(shù)相同，那么其輸出的結(jié)果也是一樣的。

平滑前、后的柏林噪聲函數(shù)曲線如圖4所示。

計算同一時刻生長點D的風(fēng)速，即

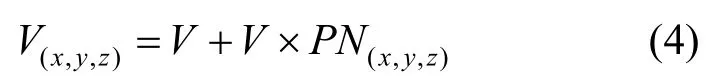
其中，V(x,y,z)為生長點D處的風(fēng)速；V為用戶輸入的風(fēng)速；PN(x,y,z)為柏林噪聲；參數(shù)x,y,z為生長點D對應(yīng)的坐標(biāo)。

自然界中風(fēng)的方向具有很大的隨機性，主要是因為風(fēng)可分為大風(fēng)和微風(fēng)。大風(fēng)特點是風(fēng)速大，同一高度平面內(nèi)的風(fēng)向大致相同且與地面平行，如圖5(a)所示，其生成的是硬凇；微風(fēng)的特點是風(fēng)速小，風(fēng)向不定，同一時刻、同一高度平面內(nèi)各方向的風(fēng)都存在且與地面平行，如圖5(b)所示，在微風(fēng)環(huán)境下生成的是軟凇。

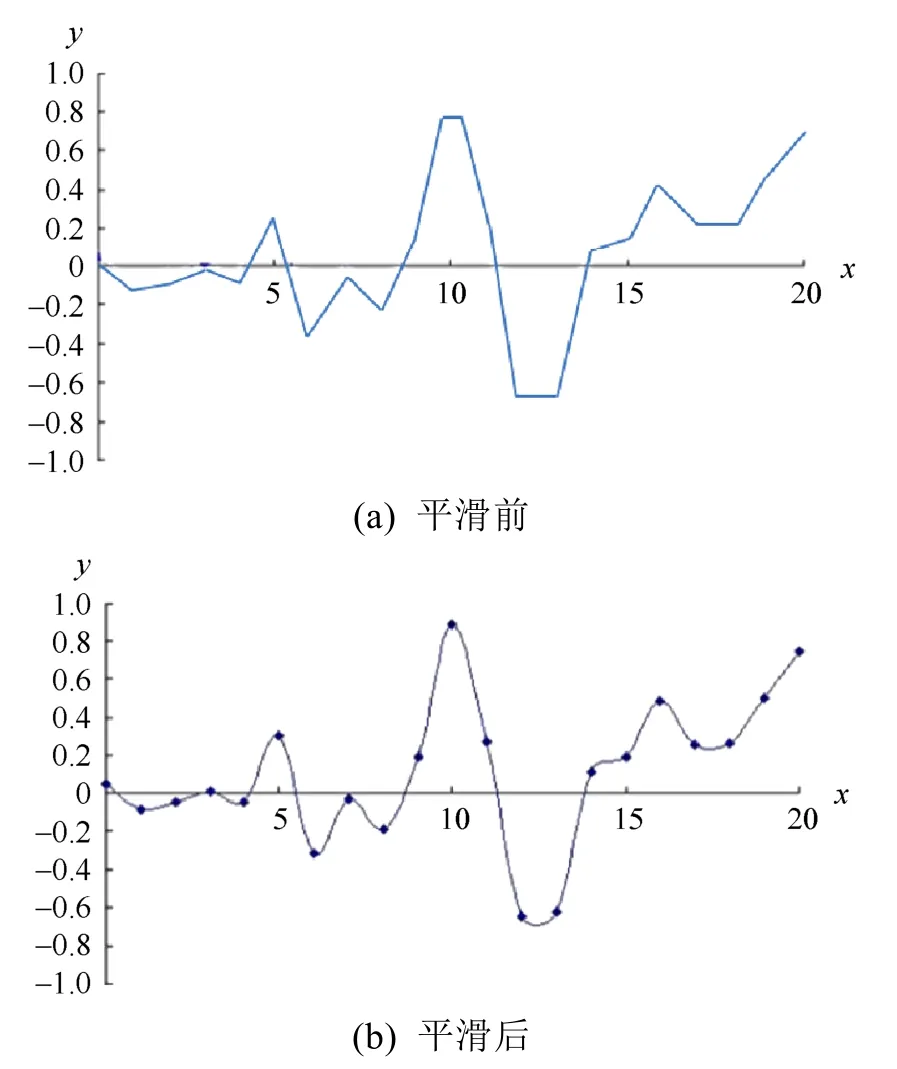
圖4 平滑前、后的柏林噪聲函數(shù)示意圖

圖5 同一高度平面內(nèi)不同風(fēng)型的風(fēng)向示意圖

因此將空間中任意一點的大風(fēng)風(fēng)向表示為Φ=(sint, 0 ,cost)，其中t為[0,2π]之間的隨機數(shù)。微 風(fēng) 表 示 為Φ=(-cost1, 0,sint2)， 其 中t1,t2∈ [ 0,2π]，t2=trand× ( 1 +Nrand)，trand為[0,2π]之間的隨機數(shù)，Nrand為通過柏林噪聲計算得到的(0，0.5)之間的隨機數(shù)。

2.4 軟凇模擬

2.4.1 軟凇生長方向

軟凇生長在風(fēng)速較小的環(huán)境中，因此其最終的生長方向由自身的生長方向與風(fēng)向共同決定。生長方向是在生長點所在三角面片的法向n添加一個隨機擾動向量得到。如圖 3所示，向量n和點D分別為三角面片法向和霧凇生長點，點E為三角面片上點D附近的一點，向量DE作為擾動向量，與風(fēng)向Φ、法向n之和得到軟凇最終的生長方向e。

2.4.2 軟凇形態(tài)

軟凇的形態(tài)類似于片狀晶體，本文利用 DLA的方法生成片狀晶體的形態(tài)。為保證最終形態(tài)的片狀結(jié)構(gòu)，首先將生長點映射到XOY平面，而后以XOY平面上的生長點為凝聚核，霧凇長度為逃逸半徑，各個粒子進行凝聚生長，凝聚過程如圖6所示。

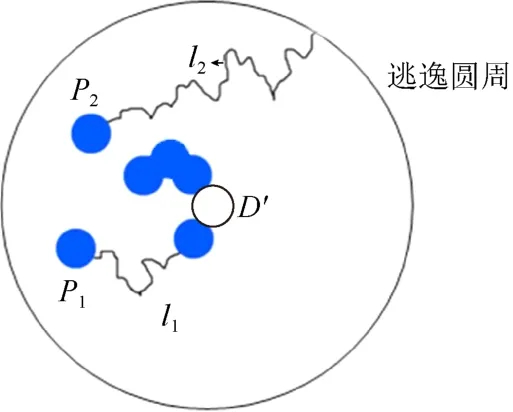
圖6 凝聚模型示意圖

D′為圖3中生長點D映射到XOY平面后的凝聚核，P1，P2分別為第1次和第2次產(chǎn)生的粒子，l1，l2是其運動軌跡。通過在半徑為Lw的逃逸圓周內(nèi)的行走，P1與凝聚體發(fā)生凝聚，P2則脫離了圓周，未與凝聚體發(fā)生凝聚。軟凇形態(tài)模擬算法如下：

(1) 將XOY平面上映射的生長點作為凝聚核D′，并設(shè)置凝聚體最大的粒子數(shù)n_max為20。

(2) 以霧凇長度Lw作為逃逸半徑畫圓，圓內(nèi)為有效區(qū)域。

(3) 在有效區(qū)域內(nèi)隨機產(chǎn)生 1個粒子，坐標(biāo)Pi(Xi,Yi)為

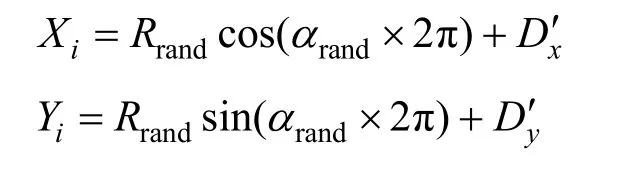
其中，Rrand為(0,Lw)之間的數(shù)，保證產(chǎn)生的粒子在有效區(qū)域內(nèi)；αrand為[0,1]之間的數(shù)；D′x和D′y分別為凝聚核的x,y坐標(biāo)。

(4) 該粒子按照一定的規(guī)律進行游走，若運動到凝聚核附近，則與凝聚核發(fā)生凝結(jié)，回到步驟(3)產(chǎn)生第2個隨機粒子；若運動到逃逸半徑之外，則直接回到步驟(3)產(chǎn)生第2個隨機粒子。

(5) 粒子每運動一次都需判斷是否到達了凝結(jié)核和已凝結(jié)的粒子附近，當(dāng)凝聚體的粒子數(shù)到達n_max后，停止產(chǎn)生新粒子，得到軟凇形態(tài)的片狀結(jié)構(gòu)。

(6) 在XOY面形成的軟凇片狀結(jié)構(gòu)旋轉(zhuǎn)到生長點所在三角面片的法向與生長方向組成的平面，得到最終的軟凇形態(tài)。

模擬過程中最重要的是粒子的行走規(guī)律。根據(jù)對流擴散方程，粒子濃度與風(fēng)速之間的關(guān)系滿足式(5)[17]，即

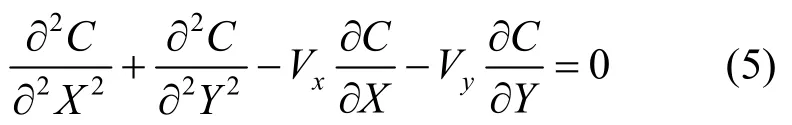
其中，C為粒子濃度；X，Y分別為粒子二維空間中坐標(biāo)的x，y分量；Vx為風(fēng)速x方向的分量；Vy為風(fēng)速y方向的分量；設(shè)?X=Δx；?Y=Δy。則粒子濃度與粒子坐標(biāo)之間的離散表示形式為

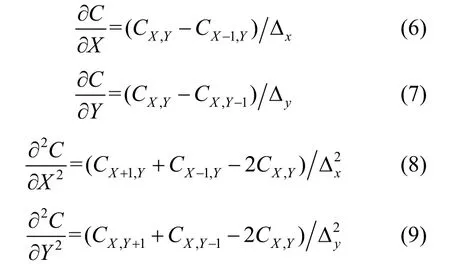
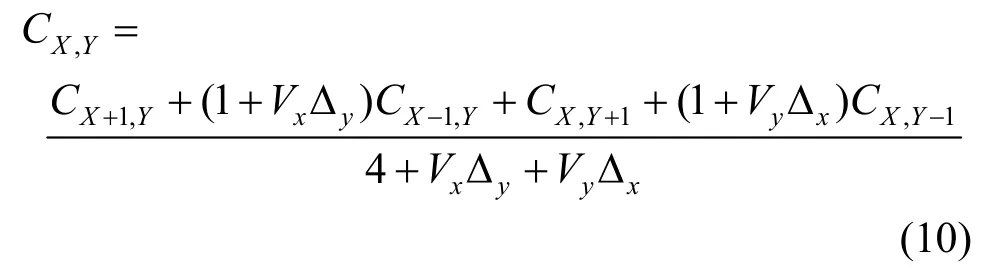
本文設(shè)粒子在行走的過程中，只會從當(dāng)前位置選擇一個四鄰域位置進行移動。在沒有任何外力場影響的純擴散條件下，從當(dāng)前位置移動到4個位置的概率是相等的，加入風(fēng)場因素之后，粒子濃度與粒子運動的概率關(guān)系[17]滿足式(11)，即

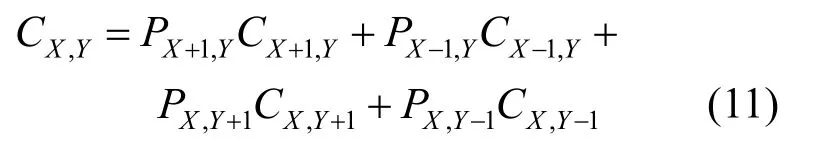
其中，PX+1,Y，PX-1,Y，PX,Y+1，PX,Y-1分別為粒子從點(X+ 1 ,Y)，(X- 1 ,Y)，(X,Y+ 1 )，(X,Y- 1 )運動到點(X,Y)的概率。由式(10)和式(11)得到粒子運動概率方程為

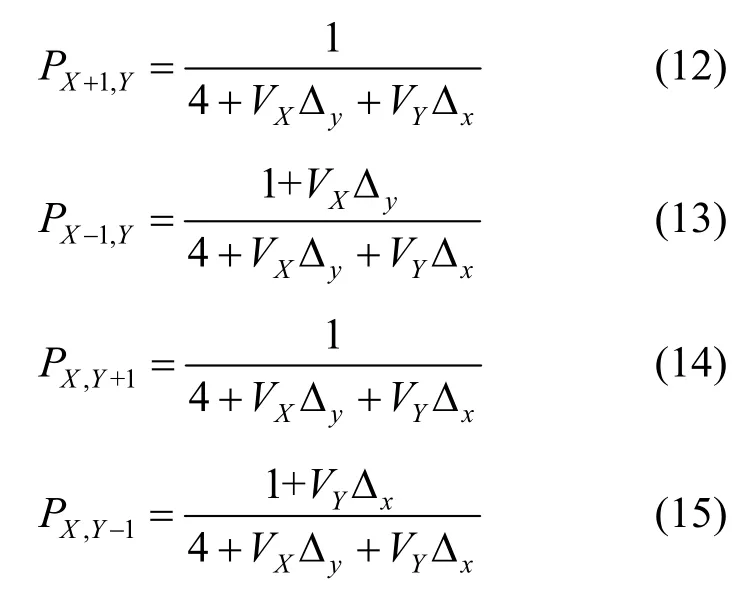
本文中 Δx, Δy的取值范圍為根據(jù)上述運動概率方程，粒子從當(dāng)前位置移動到下一位置，移動距離為 Δx, Δy，同時判斷其八鄰域內(nèi)是否存在粒子，若存在，則進行凝聚，并產(chǎn)生下一個粒子，直到凝聚體的粒子數(shù)到達n_max。

圖 7為霧滴粒子在不同風(fēng)力作用下的凝結(jié)效果示意圖，其中空心圓表示凝聚核，實心圓表示凝結(jié)體。圖7(a)是在無風(fēng)力作用的理想狀態(tài)下，使用傳統(tǒng)的擴散凝聚方法，呈現(xiàn)出類對稱性生長的凝聚體形態(tài)。圖7(b)和(c)分別是在不同風(fēng)速條件下的凝聚體形態(tài)，可以看出隨著風(fēng)速的增加，對凝聚體的形態(tài)有著非常明顯的影響作用，霧滴粒子主要在迎風(fēng)側(cè)發(fā)生凝聚，背風(fēng)側(cè)凝聚的粒子相對較少。

圖7 不同風(fēng)速下凝聚體結(jié)構(gòu)形態(tài)

2.5 硬凇模擬

硬凇的生長在風(fēng)速較大的環(huán)境中，風(fēng)對其生長方向的影響遠(yuǎn)遠(yuǎn)大于其自身的生長方向。因此本文直接將風(fēng)的方向作為硬凇的生長方向，并利用分節(jié)的方法模擬其形態(tài)，根據(jù)每一節(jié)霧凇的生長點和長度，對其受力分析，計算出下一節(jié)的生長點。

2.5.1 硬凇每節(jié)長度

硬凇每一節(jié)的長度Lwi計算公式為

其中，Lw為霧凇總長度；r為生長節(jié)數(shù)；γwi為隨機系數(shù)；i=1,2,3,···,r；γw1+γw2+γw3+···+γwi=1。

2.5.2 硬凇形態(tài)

圖8為硬凇的形態(tài)示意圖。

圖8 硬凇的模擬形態(tài)示意圖

圖 8中點D是樹模型三角面片上硬凇的一個生長點，點D1，D2，D3分別為第1節(jié)、第2節(jié)、第3節(jié)的生長終點，其之間的關(guān)系為

其中，r=1,2,3,···,Dr為當(dāng)前節(jié)的生長終點；Dr-1為當(dāng)前節(jié)的生長點，也是前一節(jié)的生長終點；Δd為風(fēng)力作用下，生長點相對于生長終點的偏移量。根據(jù)胡克定律，霧凇所受的彈力Fi滿足

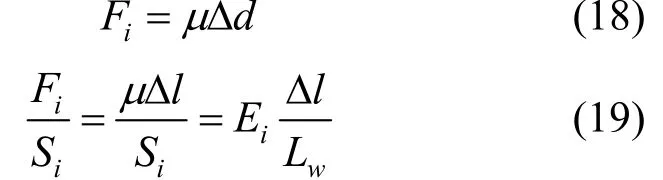
其中，μ為冰晶的剛度系數(shù)；Δd為在力的作用下的形變量，即風(fēng)力作用下霧凇生長終點相對于生長點的偏移量；Si為霧凇的面積；Ei為冰晶的彈性模量，氣溫在[-19.0，-1.0]攝氏度之間時，冰晶的彈性模量為[5.0，6.0][18]，因此Ei取[5.0，6.0]之間的隨機數(shù)；Δl為彈力作用下霧凇的形變量；Lw為霧凇的長度。化簡得到霧凇剛度系數(shù)與楊氏模量之間的關(guān)系為：μ=Ei×Wi，其中Wi為霧凇的寬度。

將式(18)帶入式(19)，得到霧凇所受彈力與偏移量的關(guān)系式為

由動量定律，可得其中，mg為風(fēng)的質(zhì)量，滿足mg=ρSg Vwt，ρ為空氣密度，取標(biāo)準(zhǔn)狀態(tài)下空氣密度值為1.29，Sg為迎風(fēng)面積，Vw為風(fēng)速。霧凇滿足受力平衡，有Fi=Fg，最終求得風(fēng)力作用下霧凇生長終點相對于生長點的偏移量Δd的橫向偏移量Δdx和縱向偏移量Δdy分別為

其中，對于軟凇，Δαi-g為霧凇生長方向與風(fēng)向的夾角；對于硬凇，Δαi-g為風(fēng)向。最終將每一節(jié)進行連接，得到硬凇的形態(tài)。

2.6 穿刺處理

在霧凇生長模擬的過程中，存在 2種穿刺現(xiàn)象：①生長出的霧凇與樹干之間的穿刺現(xiàn)象；②生長出的霧凇與霧凇之間的穿刺。如圖9所示，ΔABC是模型中一個三角面片，法向為n，生長點D1，D2，D3分別對應(yīng)3個霧凇的生長點，且生長點D3對應(yīng)霧凇發(fā)生第1種穿刺現(xiàn)象，生長點D1，D2對應(yīng)霧凇在虛線圈部位發(fā)生第2種穿刺現(xiàn)象。

對于第1種穿刺現(xiàn)象，若霧凇的生長方向e與生長點所在三角面片的法向n之間滿足：e·n≤0，則說明霧凇與樹干之間發(fā)生了穿刺現(xiàn)象，則該生長點不生長霧凇。對于第2種穿刺現(xiàn)象，設(shè)當(dāng)前霧凇的生長方向為ecurr，生長長度為lcurr，則距離當(dāng)前生長點為lcurr的所有生長點的生長方向enext分別進行相交判斷，若發(fā)生了相交，則為enext添加一個擾動使其偏離原來的生長方向。

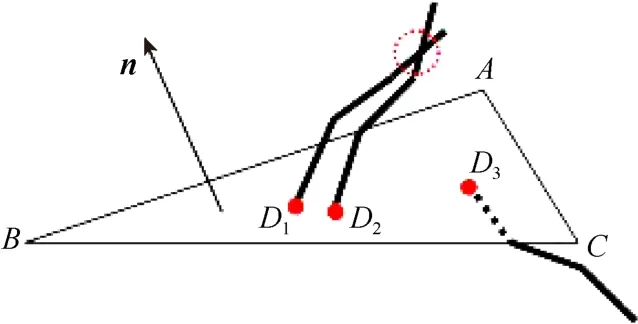
圖9 穿刺現(xiàn)象示意圖

3 實驗結(jié)果

系統(tǒng)運行在配置條件為 Intel?CoreTM i5-3230M CPU 2.60 GHz，4 GB內(nèi)存的PC機上，通過OpenGL導(dǎo)入。OBJ格式的樹模型，用povray進行渲染。圖10為軟凇和硬凇在不同環(huán)境下、同一樹枝上的模擬示意圖，生長時間分別為5 h和10 h。圖11為軟凇和硬凇結(jié)構(gòu)細(xì)節(jié)圖，圖12為渲染結(jié)果圖；圖13為軟凇在樹葉模型上的生長結(jié)果，可以看出本文算法適用于具有邊緣結(jié)構(gòu)的模型；圖14為硬凇在折斷樹枝上的生長結(jié)果示意圖，其引用了文獻[19]模型；圖15(a)為軟凇在松樹樹枝模型上的模擬結(jié)果，圖 15(b)為軟凇在松樹樹枝上生長的真實圖片；圖 16為文獻[6]利用 DLA的方法模擬出的冷表面霜晶的生長結(jié)果；圖17為霧凇細(xì)節(jié)模擬結(jié)果與現(xiàn)實的對比。表1為該樹枝上霧凇生長處理的點、面數(shù)量以及繪制時間等數(shù)據(jù)統(tǒng)計表。

圖10 不同參數(shù)控制下軟凇和硬凇模擬效果圖

圖11 軟凇、硬凇局部細(xì)節(jié)結(jié)構(gòu)模擬效果圖

圖 12 軟凇(圖(a)～(c))和硬凇(圖(d)～(f))的渲染效果圖

圖13 更多邊緣結(jié)構(gòu)生長渲染效果圖

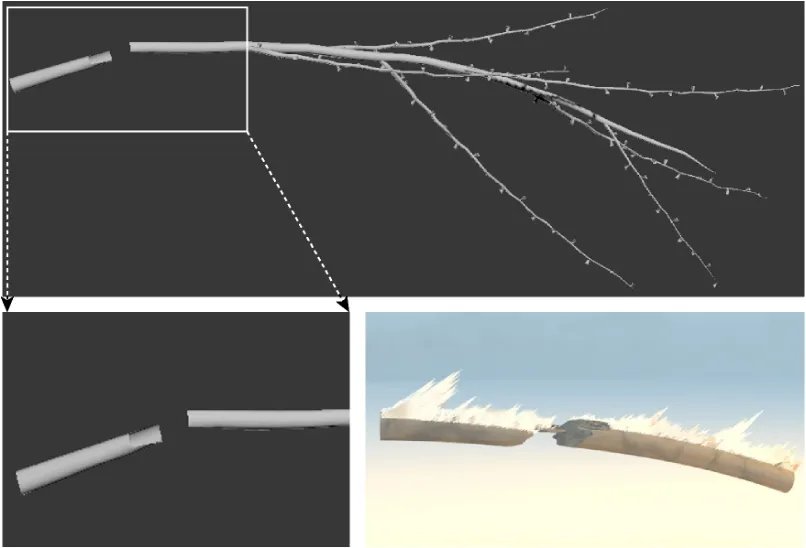
圖14 霧凇作用下樹枝斷裂效果圖

圖15 軟凇在松樹上的模擬結(jié)果圖和真實圖

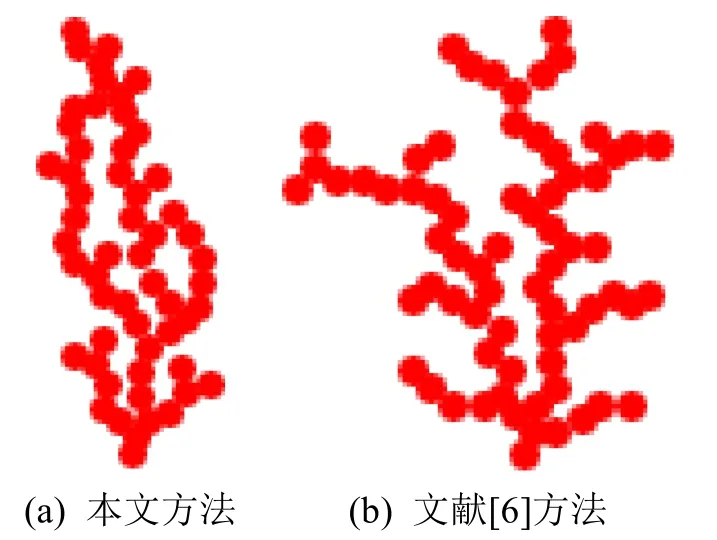
圖16 本文方法與文獻[6]方法生成的凝聚體

圖17 霧凇模擬圖與真實圖對比

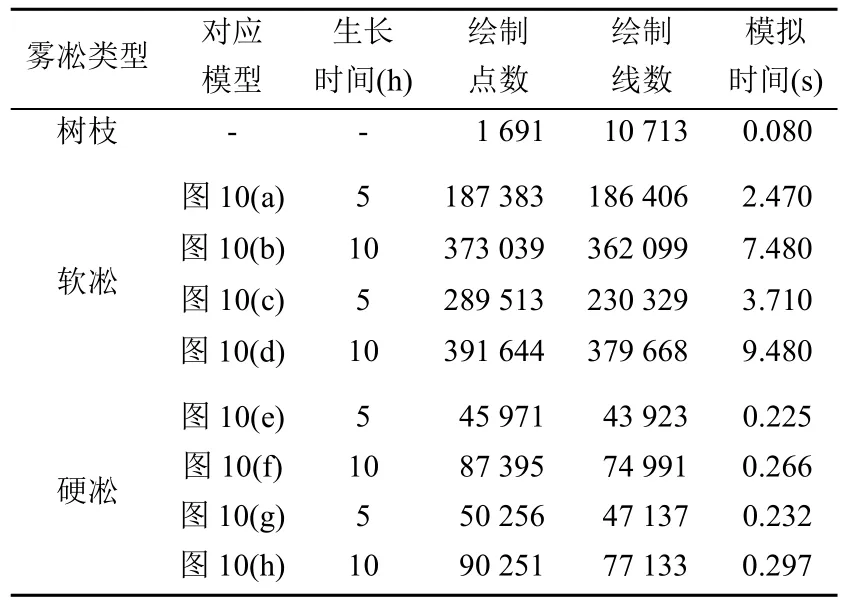
表1 樹枝模型處理參數(shù)

由表1可以看出，隨著生長時間的延長，模擬結(jié)果需要繪制的點、線數(shù)據(jù)有著明顯的增加，特別是軟凇，因軟凇的形態(tài)相對復(fù)雜需要更復(fù)雜的點、線結(jié)構(gòu)來表現(xiàn)其多樣的形態(tài)，其代價就是模擬速度明顯減慢。

圖10通過橫向2張圖片進行對比可以看出：在溫度、風(fēng)速均相同的條件下，隨著生長時間的增加，軟凇和硬凇的生長長度和密度均有明顯地增加，特別是硬凇的長度和密度，排列相對整齊，且集中在同一側(cè)，這也是對樹干、電線等被附著物產(chǎn)生巨大破壞力的原因。通過縱向5張圖片進行對比可以看出：在溫度、生長時間相同的條件下，風(fēng)速對于霧凇的形態(tài)有很大的影響作用，風(fēng)速越大，不僅會讓霧凇的形態(tài)發(fā)生明顯的變化，而且生長長度也有著非常明顯的增加。

圖16中文獻[6]方法生成的凝聚體形態(tài)更加分散且隨機性極高，更適用于理想狀態(tài)下的冰晶生長。本文方法考慮了風(fēng)對于冰晶形成過程中產(chǎn)生的影響，得到的凝聚體結(jié)構(gòu)更加緊密，且受風(fēng)向的影響較明顯，更適用于霧凇這類受周圍環(huán)境影響明顯的凝聚現(xiàn)象。但在最后的渲染結(jié)果中，文獻[6]方法增加了冰晶表面的細(xì)節(jié)，使得最后的結(jié)果更加真實自然，而本文在最后渲染中未進行霧凇表面細(xì)節(jié)的體現(xiàn)，這也是本文接下來的重點工作之一。

4 結(jié) 束 語

通過觀察、分析自然界中軟凇和硬凇的生長環(huán)境、生長形態(tài)，提出了基于物理的霧凇生長算法，主要對霧凇在環(huán)境影響下的生長形態(tài)、生長方向進行了研究。算法采用DLA的方法，考慮霧滴粒子在風(fēng)場作用下在凝聚核周圍的運動，最終形成軟凇的形態(tài)，然后對霧凇在風(fēng)力作用下進行受力分析，采用分節(jié)計算生長終點的方式模擬硬凇的形態(tài)。

本文算法對于近距離觀察軟凇和硬凇繪制效果最佳，能夠很好地展示2種霧凇的結(jié)構(gòu)、形態(tài)，對于具有一定邊緣性結(jié)構(gòu)的部位也有一定的適用性。但是對于霧凇的粗細(xì)、表面顆粒感等細(xì)節(jié)沒有進行進一步的處理，因此接下來的重點工作之一就是增加霧凇的表面細(xì)節(jié)。

對于算法的計算效率，本文提出的 算法在模擬的過程中需要處理的點線面數(shù)據(jù)量較大，導(dǎo)致霧凇生成的速度較慢，因此未來需要進一步考慮利用GPU進行加速繪制。