例談數形結合思想方法在中學數學課堂教學中的滲透

黃佩瓊

所謂數形結合，就是根據數與形之間的對應關系，通過數與形的相互轉化來解決數學問題的思想，數形結合思想是一種可使復雜問題簡單化、抽象問題具體化的常用的數學思想方法，是中學數學四大思想方法之一。在教學中構筑數形結合的平面結構，使教學活動在具體與抽象中相結合，有助于加深有關概念、性質的理解，也大大降低了學生學習的難度。把抽象的數學概念、性質與直觀的圖形有機結合起來，“難學”的數學知識便變得形象有趣，學生易學樂學。下面就談談如何在數學課堂教學中滲透數形結合思想。

一、在概念教學中滲透數形結合思想

數學概念往往是人們對概念的內涵有了深刻的認識之后才產生的，概念本身往往具有高度概括的特點，單憑描述性文字很難理解透徹。怎么辦呢？解決這一矛盾，有賴于數形結合思想的滲透。就拿數軸來說吧，一條溫度計讓學生先對數軸有了良好的感性認識，在此基礎上，結合圖形，讓他們逐步認識數軸是一條直線，是規定了原點、正方向和單位長度的直線。緊緊圍繞圖形，讓學生領會怎樣確定原點、正方向以及單位長度。特別是單位長度，更要不怕麻煩，多畫幾條數軸，使學生對“適合的長度”有深刻的認識，從而將“單位長度”和“長度單位”這一難點區別開來。也只有緊緊圍繞圖形，才能使學生領會數軸三要素缺一不可的辨證關系。當然，更重要的是，讓學生領會如何結合圖形認識數軸這一概念的思想方法。

可以滲透數形結合思想的概念很多，像相反數、絕對值等幾何概念的教學更是離不開圖形。利用圖形直觀認識概念，既符合淡化概念的大綱要求，又能達到認識深刻的目的，可謂一舉兩得。

二、在性質理解的教學中滲透數形結合思想

數學性質是解決數學問題的“武器”，想把手中兵器用得威猛、靈活，就得對其特性了如指掌，數學性質往往是靈活多變，橫向、縱向聯系多而顯得雜亂難學，在數學中滲透數形結合思想，便可輕松擊破這一難點，加深學生對性質的認識，從而運用自如。

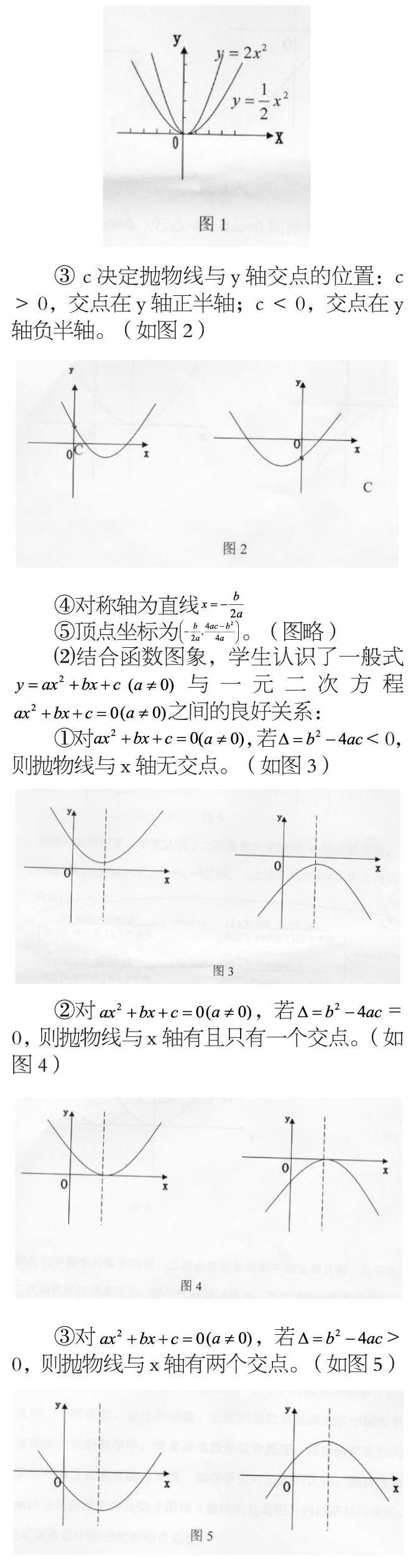
以二次函數的性質為例，如果讓學生死記硬背這些性質，必定是吃力不討好，背起來辛苦，用起來模糊。怎樣才能啃動這塊硬骨頭呢？不用急，搬來“函數的圖象”這只大幫手，讓數和形緊密結合起來，再借助多媒體教學演示圖形的變化過程，學生學習起來有趣，印象深刻。

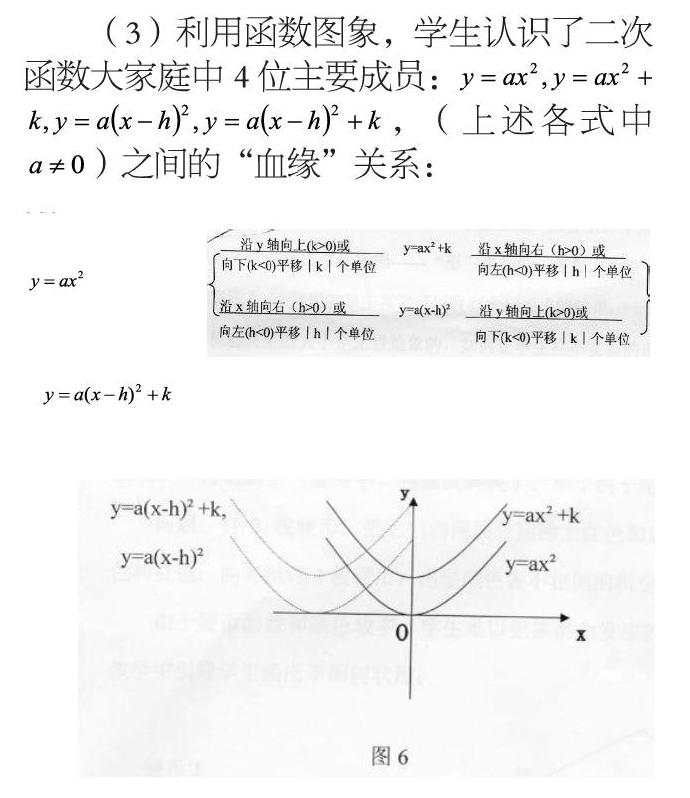
（3）利用函數圖象，學生認識了二次函數大家庭中4位主要成員： ，（上述各式中 ）之間的“血緣”關系：

函數是初中數學的重要內容，二次函數則是函數中最重要且有一定難度的部分。借助圖形這一無聲語言，讓函數性質一目了然，數與形完美的結合體現了無窮魅力，學生學習起來輕松多了。

此外，一次函數、正比例函數、反比例函數都是滲透數形結合思想的好素材。在乘法公式的教學中，更要滲透數形結合思想，依據圖形面積間的關系，幫助學生理解公式成立的合理性，加深學生對公式的認識。

三、在解題教學中滲透數形結合思想

在解題教學中，幫助學生弄清題意，分析數量關系，尋找解題途徑扮演著重要角色。對于比較復雜的題目，要想讓全體同學都能理解和領會，就不是一件容易的事;往往花費了許多口舌，學生還是一頭霧水，不知其所以然。因此，在解題教學中請出最佳搭檔——“形”來幫忙，顯得尤為重要。事實證明，畫“示意圖”在解題教學中常常可以收到水到渠成的效果。

機會發生的大小是比較抽象的，如何讓學生在不實驗的前提下得出正確判斷呢？“樹狀圖”一顯身手，問題就解決了。舉個例子：

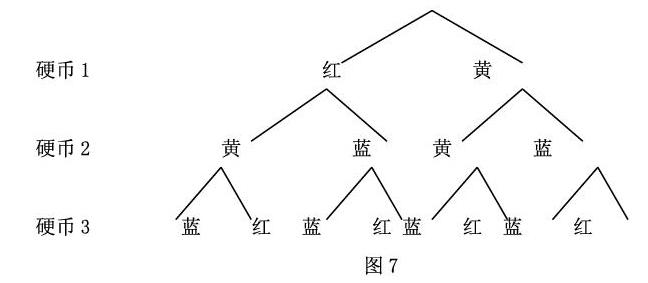
問題：有3枚硬幣，把它們的兩面分別涂上紅色和黃色，黃色和藍色，藍色和紅色;同時拋這3枚硬幣，出現顏色各不相同的機會是多少？

由于硬幣面數和顏色較多，學生難以把握機會發生的大小。因此，本人在教學中引導學生畫出下面樹狀圖：（圖7）

數學中的某些計算題，常常根據代數式的特點挖掘蘊涵的數量關系;根據一些數量關系，常常構造出由數量關系反映出的幾何圖形，根據圖形的直觀性尋求解決。

題：已知x， y均為正實數，且x+y=4， 求的最小值。

解：在本題中由求解式子的特點可以聯想到構造直角三角形利用勾股定理進行處理，構造如圖所示的圖形，BA⊥AD，CD⊥AD，垂足分別為A、D兩點，AP=x，PD=y，AD=4，AB=3，CD=2，則a=PB+PC。

此題由式子特點聯想勾股定理，構造出圖形將抽象的數學語言與直觀的幾何圖形結合起來，通過圖形的認識和數形的轉化，使問題化抽象為具體，然后運用平面圖形的幾何性質來解決。

以上各例從不同側面展現了數形結合的巧妙、新穎和簡潔有效，充分說明了數與形之間的交替和互助作用。由此可見在解題過程中，巧妙地將數與形有機地結合起來，往往能使問題的解答簡明、直觀和有趣。因此，在數學教學中，注意滲透這方面的思想，引導學生要善于將兩者巧妙地結合起來，便能學得輕松。

授人以魚，更要授之以漁。在課堂教學中滲透數形結合思想，運用數形結合的思想解決數學題，根據不同的問題相互轉化，使抽象的問題具體化，復雜的問題簡單化;利用數形結合的思想解決有關的問題不僅可以增強解決問題的靈活性，還可以提高分析問題和解決問題的效率，從而在解題中可以產生事半功倍的效果;同時也利于學生理解和接受。

參考文獻：

[1]田永東.繼承、改革、創新[J].中學數學教學參考.

[2]黃發長.讓習作成為數學學習的一道新風景[J].中學數學教學參考.

[3]付東峰.中考中的數學思想方法[M].龍門書局.