2004-2015年新疆喀什地區(qū)百日咳的動(dòng)力學(xué)建模與仿真
文靜 王建鵬 王凱

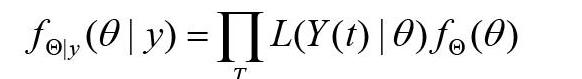
摘 要 目的:基于新疆喀什地區(qū)2004—2015年百日咳每年的新發(fā)病例數(shù)據(jù),建立動(dòng)力學(xué)模型來分析百日咳的傳播規(guī)律,為喀什地區(qū)制定百日咳控制策略提供行之有效的定量參考依據(jù)。方法:根據(jù)百日咳的傳播機(jī)制,使用傳染病動(dòng)力學(xué)建模方法構(gòu)建百日咳動(dòng)力學(xué)傳播模型,使用馬爾可夫蒙特卡羅算法(MCMC)進(jìn)行模型參數(shù)估計(jì)和拉丁超立方抽樣方法(LHS)進(jìn)行模型參數(shù)的敏感性分析。結(jié)果:分析百日咳動(dòng)力學(xué)模型,得到模型擬合結(jié)果[平均絕對百分比誤差(MAPE=19.27%),均方根百分比誤差(RMSPE=27.35%)]和基本再生數(shù)R0=11.5192[95%CI:11.4648-11.5727],說明新疆喀什地區(qū)百日咳已有成為地方病的趨勢。通過模型參數(shù)敏感性分析看到,百日咳的傳播率β、恢復(fù)率?酌和新生兒接種率p對百日咳的傳播有著重要的影響。結(jié)論:新疆喀什地區(qū)百日咳新發(fā)感染數(shù)有上升趨勢,有關(guān)部門應(yīng)加強(qiáng)對高危人群的預(yù)防與檢測,定期關(guān)注新疆喀什百日咳的傳播與流行情況,適當(dāng)擴(kuò)大監(jiān)測對象進(jìn)而有效的預(yù)防和控制百日咳病情的進(jìn)一步擴(kuò)大。
關(guān)鍵詞 動(dòng)力學(xué)模型;參數(shù)估計(jì);敏感性分析;疾病控制
中圖分類號(hào): O175;R516.6 文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.19694/j.cnki.issn2095-2457.2020.02.049
0 引言
眾所周知,百日咳(whooping cough或pertussis)是由一種百日咳鮑特菌(簡稱BP)感染所致的一種可以預(yù)防和治愈的嚴(yán)重急性呼吸道傳染病。百日咳的傳染性較強(qiáng)并且人群普遍易感。因此,百日咳的傳播對人類的健康構(gòu)成了威脅[1]。一個(gè)橫斷面的研究表明,現(xiàn)有的預(yù)防免疫控制策略對保護(hù)新生兒的作用不突出[2]。在1974年之后,全球就實(shí)施給新生嬰兒接種百白破疫苗(diphtheria,tetanus and pertussis combined vaccine,DTP)的免疫計(jì)劃,使得全球的百白破疫苗接種率達(dá)到了80%,致使百日咳發(fā)病率和死亡率急速下降,百日咳得到了非常有效的控制。但近些年,全球百日咳發(fā)病率又明顯上升,甚至在有些疫苗接種率較高的英國、美國等國家出現(xiàn)了暴發(fā)或者流行的現(xiàn)象[3], 由此可見,百日咳是一種具有復(fù)發(fā)性的傳染病。雖然百日咳可以通過接種疫苗來預(yù)防,但是接種過疫苗人群的免疫力也有一定的有效期,超過有效期的人群會(huì)回到易感的人群。
新疆地處邊疆,疫苗的接種率低于全國的平均水平,這對新疆地區(qū)百日咳的患病率會(huì)有極大影響,依照疾病監(jiān)測信息報(bào)告管理系統(tǒng)新疆百日咳2004-2012 年的疫情資料顯示:百日咳發(fā)病總數(shù)為3760 例,死亡5例,年平均發(fā)病率為2.02/10萬[4]。而喀什地處南疆地帶,根據(jù)疾病監(jiān)測信息報(bào)告管理系統(tǒng)新疆百日咳2004-2015年的喀什地區(qū)的數(shù)據(jù)顯示:新疆喀什2004 年百日咳的發(fā)病人數(shù)為388人(發(fā)病率為11/10萬人),到了2015年發(fā)病人數(shù)增加到526人(發(fā)病率為11.7/10萬人),呈現(xiàn)了緩慢上升的趨勢。因此,分析和掌握新疆喀什地區(qū)百日咳的流行趨勢來預(yù)防百日咳成為地方病是非常有必要的。本文考慮百日咳在傳播過程中的相關(guān)影響因素,建立了百日咳的傳播動(dòng)力學(xué)模型,為新疆喀什制定百日咳控制策略時(shí)提供行之有效的相關(guān)參考依據(jù)。
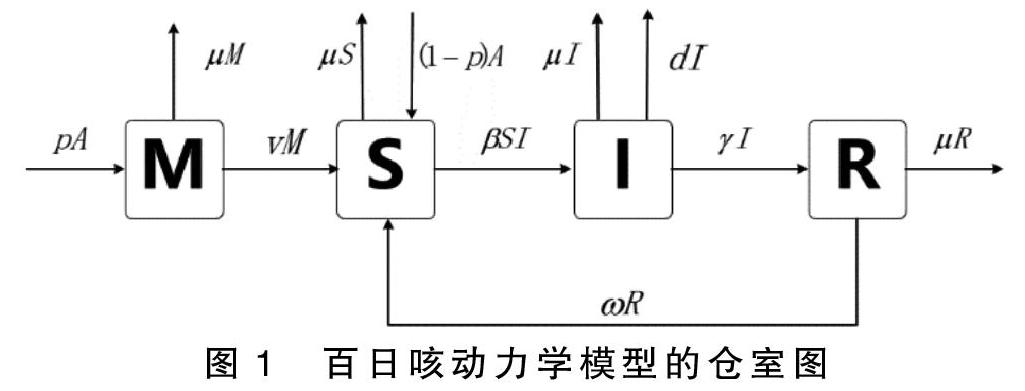
本文根據(jù)百日咳的傳播規(guī)律,將人群分為注射百日咳疫苗的新生兒(M)、易感人群(S)、百日咳感染者(I)和患病后恢復(fù)者(R)4類,構(gòu)建如下百日咳傳播的倉室模型(如圖1)。
2 模型應(yīng)用
2.1 參數(shù)估計(jì)
首先,給出模型部分參數(shù)的確定值:(1)根據(jù)疾病監(jiān)測信息報(bào)告管理系統(tǒng)2004-2012年新疆百日咳疫情資料,百日咳發(fā)病數(shù)為3760例,死亡5例[4],所以因病死亡率d取值為d=5/3760≈0.0013。(2)由文獻(xiàn)[5]可知,新疆人口的預(yù)期壽命為71.12歲,所以自然死亡率μ=1/75≈0.0141。(3)如今,百日咳疫苗覆蓋率提高到了以上[6],所以新生兒百日咳疫苗接種率。(4)根據(jù)文獻(xiàn)[7]可知,新生兒在接種百日咳疫苗12年后,隨著免疫力減弱仍有患百日咳的風(fēng)險(xiǎn),所以取υ=1/12≈0.0833。在感染百日咳病恢復(fù)后具有的免疫力期限方面,資料中沒有具體的說明,暫時(shí)估計(jì)感染百日咳病恢復(fù)后具有的免疫力期限為12年,所以恢復(fù)后免疫力減弱速速ω=1/12≈0.0833。
新疆喀什地區(qū)2004年百日咳新發(fā)病例數(shù)為388人,因此,M(t)的初始條件為M(2004)=388。假設(shè)其他初始值分別為M(0)=311679,S(0)=5000,I(0)=388,R(0)=350。
其次,根據(jù)模型(1)和馬爾可夫蒙特卡羅算法(MCMC)來估計(jì)參數(shù)β和?酌。我們將累積病例建模為泊松分布的隨機(jī)變量,因?yàn)椴此煞植济枋隽嗽谝欢螘r(shí)間內(nèi)觀察到的事件的數(shù)量。我們通過采樣校準(zhǔn)模型參數(shù)的后驗(yàn)分布向量θ|y={β,?酌}|y,向量y源于Y(t)=βSI,Y(w)表示被報(bào)道的累積病例。我們用Metropolis-Hastings接受準(zhǔn)則,通過馬爾可夫鏈蒙特卡洛進(jìn)行抽樣。后驗(yàn)密度為
前密度fΘ(θ)是兩個(gè)單變量的聯(lián)合概率先驗(yàn)。我們認(rèn)為β和?酌是基于U(0,1)的分布,程序可在R3.3.1版本中實(shí)現(xiàn)。我們從30000個(gè)迭代中采樣,并將前200個(gè)樣本作為一個(gè)老化周期樣本去掉。在這28000個(gè)樣本的基礎(chǔ)上,計(jì)算出基本再生數(shù)R0的點(diǎn)估計(jì)值和的置信區(qū)間,并根據(jù)現(xiàn)有的參數(shù)值計(jì)算出三種分布對R0的貢獻(xiàn)。結(jié)果如表1所示。
最后,計(jì)算出基本再生數(shù)R0=11.5192,其中R0的95%置信區(qū)間為95%CI:11.4648-11.5724,R0的取值范圍具體如圖2。
2.2 模型評價(jià)
用已建立的傳染病動(dòng)力學(xué)模型擬合新疆喀什2004-2015年百日咳的累積發(fā)病數(shù),圖3表明實(shí)際的累積發(fā)病數(shù)的點(diǎn)在曲線附近分布,并且置信帶較窄,MAPE=19.27%,PMSPE=27.35%,MAPE與RMSPE均<50%,顯示模擬結(jié)果比較合理,并且MAPE在19%-20%之間,且MAPE與RMSPE均<30%,說明建立的模型擬合效果良好。
2.3 模型參數(shù)敏感性分析與疾病控制
拉丁超立方抽樣的不確定性和靈敏度分析已被廣泛應(yīng)用于傳染病模型[9-11]。因此,為了檢驗(yàn)?zāi)P偷母鱾€(gè)參數(shù)變化的敏感性,分析出各個(gè)因素對模型結(jié)果的影響程度,使用拉丁超立方抽樣樣本作為R0的樣本參數(shù)[8]來計(jì)算基本再生數(shù)R0表達(dá)式中各個(gè)參數(shù)的偏秩相關(guān)系數(shù)(PRCC)值與P值。模型中各個(gè)參數(shù)的(PRCC)值對基本再生數(shù)R0的影響為:參數(shù)的PRCC值中絕對值中相較大的,對于基本再生數(shù)R0的變化影響更大。正號(hào)或負(fù)號(hào)分別表示影響是正或是負(fù)。本文選擇樣本大小n=1500,參數(shù)d,β,?酌,ω,μ,p和υ作為輸入變量,R0作為輸出變量。共計(jì)7個(gè)參數(shù)的PRCC值與P值如表2。表2 顯示了因病死亡率d(PRCC=-0.8310)對R0有最大的影響,緊隨其后的是凈死亡μ(PRCC=-0.7845), 其次是患百日咳病率β、患百日咳病后的恢復(fù)率?酌、新生兒百日咳疫苗接種率p和接受百日咳疫苗的免疫力減弱速度υ。7個(gè)參數(shù)對R0的敏感性如圖4所示。圖4 顯示了β和υ對R0有正面影響,而d,?酌,μ和p對R0有負(fù)面影響;同時(shí)看出,參數(shù)ω作為假設(shè)值,R0對ω不敏感(P>0.05),而其他參數(shù)均具有統(tǒng)計(jì)學(xué)意義。因此,從以上敏感性分析看到,從實(shí)際情況出發(fā),控制百日咳的流行和傳播最有效的方法是減少參數(shù)β的值和增加參數(shù)ω和p的值。
在上述工作的基礎(chǔ)上進(jìn)一步討論參數(shù)β、?酌和p對R0的影響。控制其他參數(shù)不變的情況下,使用軟件分別畫出β與R0、?酌與R0和p與R0之間的關(guān)系變化圖。
為了使R0保持在1e-06到5.42e-05之間,控制其他參數(shù)不變時(shí),R0隨著β變化的情況如圖5所示。圖5表明了R0隨著百日咳的患病率β的增加而增加,患病率β的曲線與直線R0=1相交于點(diǎn)(4.7e-06,1)。則說明當(dāng)百日咳的患病率β<4.7e-06的時(shí)候,可以采用控制百日咳的患病率的方法來有效控制百日咳的傳播。
為了使患百日咳后恢復(fù)率?酌保持在1到20之間,控制其他參數(shù)不變時(shí),R0隨著?酌變化的情況如圖6所示。圖6表明了R0隨著患百日咳病后恢復(fù)率?酌的增加而減少,恢復(fù)率?酌的曲線與直線R0=1相交于點(diǎn)(11.8,1)。則說明當(dāng)患百日咳后的恢復(fù)率?酌>11.8時(shí)有R0<1, 可采用控制患百日咳病后恢復(fù)率的方法來控制百日咳的傳播。
根據(jù)實(shí)際情況,新生兒的百日咳疫苗接種率p需控制在0到1之間,控制其他參數(shù)不變時(shí),R0隨著疫苗接種率p變化的情況如圖7所示,圖7表明了R0隨著疫苗接種率p的增加而減少,從圖中可看出,疫苗接種率p=1時(shí),R0為11.34,也就是點(diǎn)(1,11.34),則說明即使疫苗接種率p增加到100%,R0的值也很大。從圖7也可看出,疫苗接種率p對R0是有效的,但是并不是最有效的控制,這也與表2中的PRCC與p值相吻合。
綜合以上考慮因素把減少百日咳的患病率、增加患百日咳病后的恢復(fù)率和增加新生兒的疫苗接種率相結(jié)合起來,就可以更加有效地控制百日咳的流行與傳播。
3 討論
百日咳對于新疆來說,在2004-2015年間每年發(fā)病率都有不同程度的上升趨勢,而喀什地區(qū)是全疆地區(qū)百日咳發(fā)病情況的高發(fā)區(qū)[12],因此,喀什百日咳的流行和傳播情況對全疆百日咳疫情都會(huì)有較大的影響。新疆喀什地區(qū)在2004-2015年間,百日咳每年平均發(fā)病率為4.73/10萬人,這12年中2015年的發(fā)病率是最高的,高達(dá)11.7/10萬人,在全疆位居前列。因此,為了研究新疆喀什百日咳的傳播與流行情況,本文根據(jù)百日咳的發(fā)病機(jī)理構(gòu)建傳染病動(dòng)力學(xué)模型,使用馬爾可夫鏈蒙特卡羅算法(MCMC)估計(jì)模型參數(shù)β=5.42E-05和?酌=1.0116。算出了喀什地區(qū)的基本再生數(shù)R0=11.5192(95%CI:11.4648-11.5724),這表明百日咳在新疆喀什已經(jīng)呈現(xiàn)出流行的趨勢。通過模型擬合,擬合精確度指標(biāo)與均,說明建立的模型擬合效果良好,具有一定的可信度。使用拉丁超立方抽樣方法(LHS)進(jìn)行模型參數(shù)的敏感性分析,結(jié)果表明百日咳的患病率β和患百日咳病后的恢復(fù)率?酌是影響百日咳傳播與流行的主要影響因素,新生兒的百日咳疫苗接種率p是有效的控制因素但相比前兩個(gè)參數(shù)不顯著。
因此,本文給出如下一些控制新疆喀什地區(qū)百日咳疾病的措施:(1)降低百日咳的患病率;具體做法:新疆是溫帶大陸性氣候,環(huán)境干燥,加之南疆的日照少,而喀什就處在南疆,那么可以通過適當(dāng)?shù)耐獬龌顒?dòng)來提高免疫力。(2)提高患百日咳病后的恢復(fù)率;具體做法:提示醫(yī)護(hù)人員在診斷中要提高警惕,百日咳的癥狀與普通感冒相似,應(yīng)加強(qiáng)對百日咳的血清監(jiān)測,及時(shí)發(fā)現(xiàn)和確定是否患百日咳病,以便于及時(shí)發(fā)現(xiàn)盡早隔離治療,防止病情的惡化和傳染給其他人。(3)增加疫苗的接種率;具體做法:百日咳是一種可以傳染的疾病,但是是可以預(yù)防的,嚴(yán)重時(shí)還會(huì)導(dǎo)致死亡,新生兒可以通過接種疫苗來預(yù)防這種疾病的發(fā)生。至今為止,預(yù)防百日咳最經(jīng)濟(jì)有效的方法就是通過接種百日咳疫[13],所以應(yīng)該提高新疆地區(qū)的百日咳疫苗接種率和全程接種率,定期進(jìn)行百日咳疫苗的查漏補(bǔ)種工作,以此來降低百日咳的發(fā)病率。
綜上所述,要完全控制或消滅百日咳的傳播與流行是有一定難度的,因此,相關(guān)部門應(yīng)做好預(yù)防措施,防患于未然,定期關(guān)注新疆喀什百日咳的傳播與流行情況,適當(dāng)擴(kuò)大監(jiān)測對象進(jìn)而有效的預(yù)防和控制百日咳病情的進(jìn)一步擴(kuò)大。
參考文獻(xiàn)
[1]張柳,趙建宏,張庶民.百日咳流行病學(xué)研究進(jìn)展[J].中國疫苗和免疫,2008,14(6):559-564.
[2]徐勇勝.百日咳臨床特征研究進(jìn)展[J].中國實(shí)用兒科雜志,2016(9):712-715.
[3]許紅梅,鄭佳佳,XuHongmei,等.百日咳臨床特點(diǎn)及流行病學(xué)研究進(jìn)[J].中華實(shí)用兒科臨床雜志,2014,29(22):1681-1682.
[4]陳濤,謝娜,甫爾哈提·吾守爾,等.2004-2012年新疆維吾爾自治區(qū)百日咳流行特征分析[J].疾病監(jiān)測,2013,28(11):911-913.
[5]羅冬梅,吳順華,王凱.新疆巴州地區(qū)梅毒的動(dòng)力學(xué)建模與仿真[J].中華地方病學(xué)雜志,2017,36(7):542-546.
[6]Althouse B M,Scarpino S V.Asymptomatic transmission and the resurgence of Bordetella pertussis.[J].BMC Medicine,13,1(2015-06-24),2015,13(1):146.
[7]李樹堂.成人也會(huì)患百日咳[J].大家健康,1996(12):16-17.
[8]Marino S,Hogue I,Ray C,Kirschner D.A methodology for performing global uncertainty and sensitivity analysis in systems biology. Journal of theoretical biology.2008;254(1):178-196.
[9]Blower S,Mclean A,Porco T,Small P,Hopewell P,Sanchez M,et al.The intrinsic transmission dynamics of tuberculosis epidemics.Nature medicine.1995;1(8):815-821.
[10]Blower S,Dowlatabadi H.Sensitivity and uncertainty analysis of complex models of disease transmission:an HIV model,as an example. International Statistical Review/Revue Internationale de Statistique.1994;229-243.
[11]Sanchez M,Blower S.Uncertainty and sensitivity analysis of the basic reproductive rate:tuberculosis as an example.American Journal of Epidemiology.1997;145(12):1127-1137.
[12]陳佳,謝娜,吳秀峰等.基于ARIMA乘積季節(jié)模型的新疆喀什百日咳流行趨勢分[J].新疆醫(yī)科大學(xué)學(xué)報(bào),2017,40(3):380-384.
[13]BLACK RE,COUSENS S,JOHNSON HL,et al.Global,regional,and national causes of child mortality in 2008:a systematic analysis[J].Lancet,2010,375(9730):1969-1987.

