一種改進的非定常激波裝配算法

常思源，白曉征，崔小強，劉君,*

1. 大連理工大學 航空航天學院，大連 116024 2. 中國人民解放軍95791部隊，酒泉 735018

在可壓縮非定常流動中，激波的產生、傳播及其與幾何邊界的相互干擾，往往支配著整個流動的特性。在計算流體力學(CFD)領域中，一些學者采用激波捕捉(Shock-Capturing, S-C)法研究激波與湍流/聲波的干擾時，發現激波處產生的非物理波動會顯著降低下游流場的精度，即無論格式的設計精度有多高，激波下游的流場難以恢復到應有的格式精度[1-2]。

本質上講，這些缺陷的根源在于激波捕捉格式的基本構造，即捕捉的激波等強間斷往往會跨越若干網格點，而這些節點上的參數僅僅是由人為引進而來的，絲毫不能反映真實間斷內部的流動結構[3]。因此近年來有很多學者在認識到捕捉法的先天不足后，堅信只有類似激波裝配(Shock-Fitting, S-F)的算法才能從根本上解決這些問題[2,4-5]。

傳統激波裝配法主要基于結構網格框架，取得了一系列卓有成效的研究成果[6-8]。然而，考慮到其深受網格拓撲限制、算法邏輯比較復雜及程序移植性差等缺點，因此近年來激波裝配法的研究熱點逐漸轉移到較為靈活的非結構網格算法框架。經過十幾年的發展，基于非結構網格的激波裝配法已成功應用于一些超/高超聲速、二/三維定常流動問題[9-11]，然而將其拓展到復雜的非定常流動中仍然困難重重，目前僅有一些探索性的嘗試。

2016年，Bonfiglioli等成功將其基于非結構網格和格點型有限體積法的裝配算法[9]拓展到非定常計算并模擬了激波與渦的相互作用[12]，隨后又進一步模擬了運動激波正規反射問題[13]；劉君等模擬了運動激波與氦氣柱的相互作用，采用裝配方法對氣柱界面進行裝配，而運動激波仍用捕捉法進行模擬[14]；隨后，鄒東陽等對等截面通道內的運動激波進行裝配，與理論值比較考察了算法的計算精度[15]；此外，作者所在團隊采用邊界裝配策略對超高速彈丸發射時頭部大范圍運動的強激波進行處理，拓展了裝配法在此類問題中的應用[16]。然而，從以上研究來看，裝配的激波只在直壁面上運動，而對于激波在彎曲壁面上的傳播并未涉及；在整個計算中，裝配的激波陣面大多不能自發地實現大變形，如拉伸、縮短和彎曲，往往需要人為調整改變裝配激波點的分布；且當激波運動致使流場網格質量變差時，經常需要人為重新替換網格，算法的自動化程度比較低，計算代價比較大；最重要的一點，由于缺少成熟有效的基于非結構網格的運動激波探測(Shock Detection)算法，目前尚不能自動處理激波發生拓撲變化這類情況[12]，如激波的正規反射向馬赫反射演化、激波的新生與弱化等。

針對上述前3個問題，本文在近年來發展的自適應間斷裝配求解器(Adaptive Discontinuity Fitting solver，ADFs)[17]的基礎上進行了若干算法改進，實現了裝配激波點在曲壁面上的運動；通過自動調整間斷節點的分布，保證了激波陣面在演化中不失真；局部自動網格重構策略的實現大大減少了人為干預，顯著提高了算法的計算效率；此外，結合數值算例，提出了一種針對激波干擾點運動的裝配策略。仿真結果表明了算法的合理性和有效性。

1 自適應間斷裝配求解器

本節首先對激波捕捉算法和以此為基礎發展而來的ADFs進行簡單介紹，然后重點說明針對非定常問題的一些改進。

1.1 激波捕捉算法

考慮網格運動變形，控制方程采用任意拉格朗日-歐拉(Arbitrary Lagrange-Euler，ALE)法描述的二維可壓縮非定常Euler方程的積分形式：

(1)

式中：Q為守恒變量；Fc為對流項通量；xc為網格運動速度；n為控制體表面外法向單位向量；V和S分別表示控制體和控制體表面；dσ和dψ分別表示體積微元和面積微元；ρ為密度；ui為速度；E為單位質量流體總能；p為壓強；δij為Kronecker函數；考慮量熱完全氣體，比熱比γ=1.4。

數值計算采用格心型有限體積法，流場變量僅存儲在網格單元中心。不特別說明，本文均采用AUSM+(Advection Upstream Splitting Method+)格式計算面元對流通量，采用顯式4步Runge-Kutta格式進行時間推進，以此保證在光滑流場中時空離散上均具有二階精度。

非結構動網格技術方面，本文利用改進后的彈簧近似法[18]，避免網格在變形運動中出現失效單元，保持較好的網格質量，且不會造成求解器計算效率的大幅度降低。此外，當流場邊界因出現大變形、大位移而導致網格質量急劇下降時，往往需要進行網格重構。這又涉及到新/舊網格間的流場信息傳遞，為了盡量減小插值引起的空間精度下降和非物理振蕩，本文采用基于單元相交的混合網格精確守恒插值方法[19]。同時，為了防止因網格運動引入非物理解，還需要根據“離散幾何守恒率”對計算方法進行修正。由于篇幅所限，相關算法這里不再詳述，可參考文獻[18]。

1.2 自適應間斷裝配算法

1.2.1 標記間斷位置

在使用激波裝配法時，首先都需要給定擬裝配的初始間斷位置。一般來說，對于定常流動，只需給定大概位置，不要求十分準確，隨著流場收斂間斷最終便會移動到準確的位置[17]；然而，對于間斷處于不斷運動的非定常流動，初始間斷位置的標記比較重要，若偏差過大可能會嚴重影響后續流場的演化。

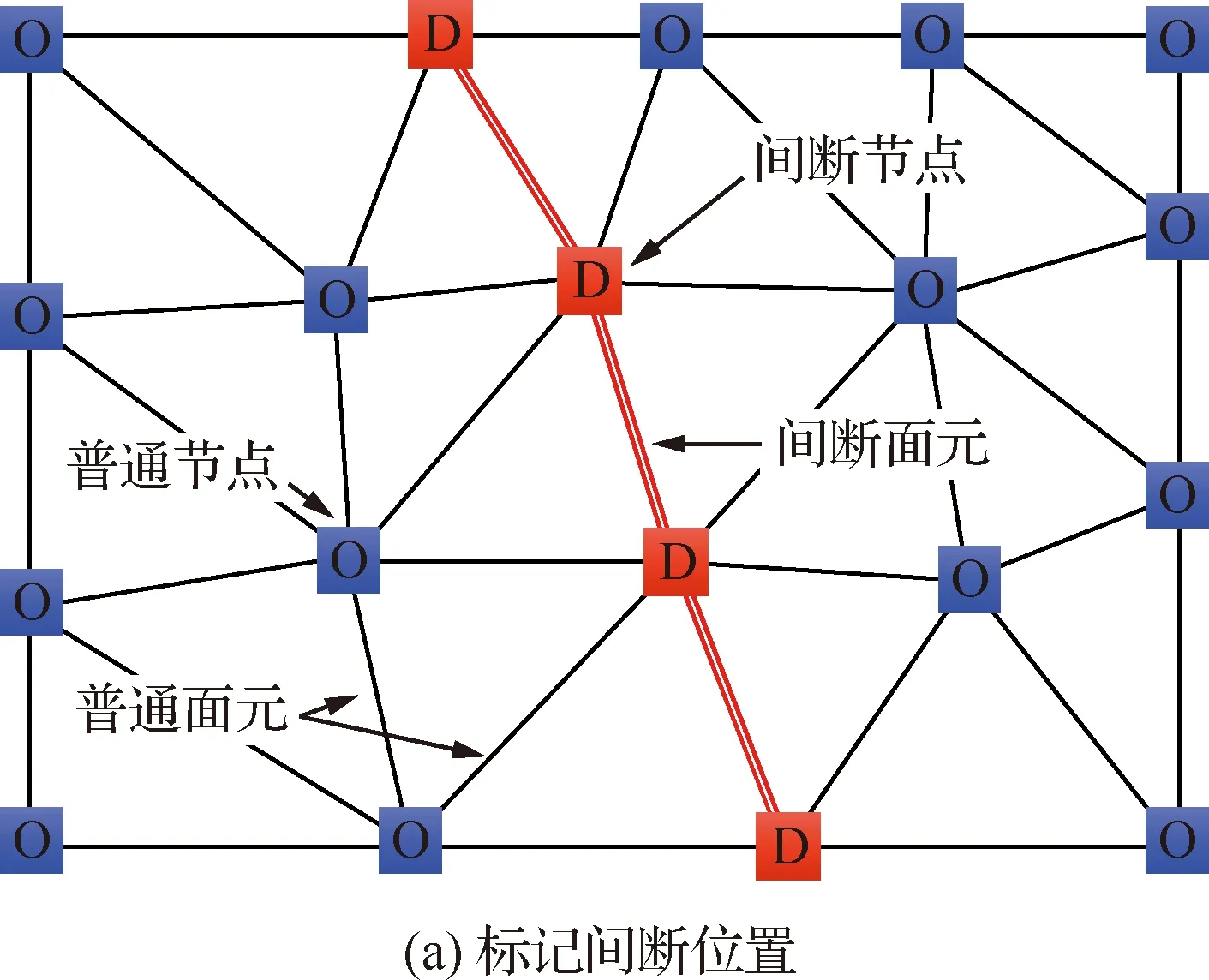
圖1 自適應間斷求解器的關鍵步驟

如圖1(a)所示，ADFs通過指定網格節點的屬性(間斷或普通)來標記間斷的位置，間斷陣面由一系列間斷面元組成，而間斷面元同時也作為流場網格單元的邊界；每個間斷陣面上的間斷節點均存儲兩組流場數據，分別對應間斷兩側的狀態。特別地，對于由m條間斷匯聚的干擾點，則該點將存儲2m組流場參數，分別對應m條間斷的兩側。

1.2.2 初始化間斷節點參數

對于格心型有限體積法，已知t時刻的流場數據僅存儲于所有網格單元中心。考慮到ADFs的裝配計算是建立在網格節點上的，因此采用反距離加權(Inverse Distance Weighted)法，如圖1(b)所示，由間斷兩側貢獻單元的格心值(Uu和Ud)插值得到所有間斷節點兩側參數(Vu和Vd)，即

(2)

此外，間斷節點j的法向構造如下：

(3)

1.2.3 計算并修正間斷節點參數

1.2.2節得到的間斷節點兩側參數并不滿足描述間斷的跳躍關系式，如Rankine-Hugoniot(R-H)關系式。對激波來講，在激波坐標系下，由于上游流動是超聲速的，即下游流動信息理論上不會污染上游參數，因此上游流動參數Vu無需修正。沿著間斷節點法向n，一共有4個參數需要計算，即修正后的激波下游流動參數V′d=[ρ′d,u′d,p′d]和激波節點的運動速度ω=ω·n。R-H關系式和下游特征相容關系式分別為

(4)

(5)

聯立式(4)和式(5)即可求得V′d和ω。

此外，在求得激波節點運動速度后，便可以計算出間斷節點在激波坐標系下的上游相對馬赫數為

(6)

1.2.4 網格節點運動

(7)

如圖1(d)所示，通過彈簧近似法便可求得流場其余所有普通節點在新時刻的位置，從而更新得到新的流場網格。值得注意的是，對于定常流動，最終ω將趨于0，即間斷位置收斂，流場網格將不發生變形。

1.2.5 流場更新

基于新的流場網格，采用1.1節所述的激波捕捉求解器進行流場更新，獲得t+Δt時刻各個網格單元的格心值，為此需要計算各個面元的對流通量。對于普通面元，仍可以采用各種空間離散方法進行通量分解計算，無需任何修正；而對于間斷面元，其通量可以根據上游參數直接寫出：

(8)

最后，通過時間推進算法便可得到t+Δt時刻的流場，重復1.2.1節～1.2.5節的步驟進行下一時間步的裝配計算直到計算終止。

1.3 非定常激波裝配的一些改進

非定常激波相比定常激波的一個顯著特點是其陣面的位置或形狀會隨時間發生變化，因此算法需要具備有效模擬激波形狀或長度發生劇烈變化的能力。本節針對運動激波傳播特性，對ADFs進行相應的改進，使其能準確高效地模擬激波運動問題。

1.3.1 間斷節點沿壁面運動

采用ADFs模擬管道中的運動激波時，需要對沿壁面運動的間斷節點進行特殊處理。根據壁面的彎曲特性，一般可以將其分為直壁面和曲壁面兩大類，對兩者的處理有明顯區別。

對于直壁面，如圖1(d)所示，間斷節點可以沿壁面方向自由滑動，不需要跨越任何壁面網格節點；而間斷附近的壁面節點根據非結構動網格技術調整位置，同樣沿壁面滑動，不會破壞直壁面的形狀。

對于曲壁面，處理要復雜一點，由于其是由一系列非共線的小直線段(壁面網格面元)離散的，為了保證貼體特性，曲壁面上的網格節點在計算中通常固定不動，因此間斷節點必然會跨越壁面網格節點。針對彎曲方向的不同，曲壁面又可分為凸曲壁和凹曲壁，兩者的處理方式略有差異，下面簡要介紹。

如圖2所示，用i、j、k、m、n表示各個網格節點。在t時刻，間斷節點i沿面元mk向壁面節點k滑動，根據間斷節點沿壁面運動速度ωt,i，若計算有ωt,iΔt>lik，其中lik為節點i、k之間的距離，則說明下一時刻間斷節點i將跨越節點k。

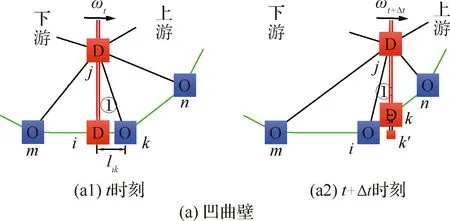
圖2 間斷節點沿曲壁面的運動

在確定t+Δt時刻新的壁面間斷節點位置時，首先根據式(7)計算出間斷節點i的虛擬推進位置k′；對于凹曲壁(見圖2(a2))，新間斷節點取直線jk′與面元in的交點；對于凸曲壁(見圖2(b2))，過點k′作面元in的垂線，新間斷節點取垂足。

實際上，從動網格角度考慮，該過程相當于間斷節點i移動到了壁面網格節點處并退化成普通節點，而對應壁面網格節點k移動到新的壁面間斷位置并轉化成間斷節點。從間斷角度考慮，相當于間斷節點跨越了運動方向上鄰近的曲壁面網格節點。值得注意的是，在跨越前后，由節點i、j、k組成的三角形網格單元①從激波上游移動到了激波下游，因此需要對其格心參數重新進行賦值，直接由間斷節點下游激波參數插值即可得到。

1.3.2 間斷節點分布的自動重構

對于定常間斷裝配，由于間斷移動變形有限，通常間斷節點能維持較好的分布；在前期的一些裝配計算中，若有必要調整間斷節點分布時，通常要人為重新劃分網格[17]，費時費力。而間斷在移動過程中往往會不斷變長或縮短，從而造成相鄰間斷節點的間距過大或過小，使得間斷陣面附近的網格質量迅速下降，如圖3所示。當這種情況發生時，需要沿間斷陣面重新調整間斷節點分布，使其間距近似等于周邊網格單元的尺寸。對于二維問題，具體步驟如下：

圖3 間斷節點分布重構前后的網格

步驟1判斷間斷節點是否滿足分布重構條件關系式：

lk/lave<δmin或lk/lave>δmax

(9)

式中:lk為第k個舊間斷面元的長度；lave為間斷鄰近網格單元的平均尺度；δmin和δmax分別為預設的最小間距和最大間距系數，通常取0.3和1.7。

步驟2對需要分布重構的各組間斷散點進行排序并曲線擬合。考慮到每條間斷陣面的始點和終點在重構前后的位置固定，本文采用多次Bézier曲線擬合法[20]得到各條間斷擬合曲線。

步驟3將擬合曲線按照尺寸βlave進行平均分割獲得各個均分點。為了更好地描述曲線的彎曲程度，用β來控制均分點的疏密程度，對較為平直的曲線，β通常取1.2；而對于比較彎曲的曲線，β通常取0.7。

步驟4將均分點映射到舊間斷面元上從而得到分布重構后的間斷節點。注意，如果不進行映射，直接采用均分點作為新間斷節點，會在一定程度上損失位置精度，當進行多次分布重構后位置誤差積累可能造成間斷位置形狀出現顯著偏差。

步驟5基于新的間斷節點，重新劃分間斷附近網格，通過插值算法獲得新網格單元格心的流場參數。

該方法不僅用于間斷節點的分布重構，同樣，當間斷節點在直壁面上滑動時，若干壁面網格節點難免會過近或過遠，此時便需進行壁面網格節點的分布重構。

1.3.3 流場網格的局部自動重構

對于定常激波裝配，由于間斷陣面的變形幅度較小，一般只需進行幾次網格重構即可，可以輸出網格并導入專業CFD網格生成軟件(如Pointwise)人工生成網格，然后再讀入網格完成重構過程。而對于運動激波裝配，由于網格變形比較劇烈，需要頻繁重構網格，若再進行人工手動重構將付出極大的計算代價，嚴重影響計算效率，因此需要高效的自動網格生成策略。

本文成功將Shewchuk研發并開源的二維Delaunay三角形網格生成程序“Triangle”[21]嵌入到ADFs中，實現了流場網格的自動重構。下面以一道右行激波在平直管道中運動為例，通過展示若干關鍵時刻的流場網格，來具體說明該重構策略的特性：

1) 采用局部網格變形/重構策略能顯著提高計算效率，同時重構單元數量的縮減很大程度上可以減小流場信息插值引入的誤差。如圖4(a)所示，以間斷位置作為起點向兩側搜尋網格，標記距離間斷最近的n層網格單元作為可變形單元且可以重構，其他網格靜止且不參與重構，即流場可分為“動網格區”(圖4陰影區)和“靜網格區”。當激波在直壁面上運動時，n通常取10；而在曲壁面上運動時，由于網格重構較為頻繁，動網格區可以取小一點，如n=3。

2) 當激波運動使得網格質量較差時(如圖4(b))，需要進行網格重構。考慮到計算初始網格通常用專業網格生成軟件劃分，網格質量可以控制得比較好(如大部分為正三角形)，因此ADFs在網格重構時利用了初始網格信息。如圖4(c)所示，提取位于重構區內的初始網格點，作為網格生成“控制點”供Triangle程序調用生成Delaunay三角形網格。注意，為了保證網格質量，距離間斷過近(約一個網格尺寸內)的初始網格點不作為控制點。這樣，經控制生成的大部分網格單元的尺寸和形狀與初始高質量網格保持一致(對比圖4(a)與圖4(c))，一定程度上減弱了網格重構對流場網格分布和拓撲的影響。

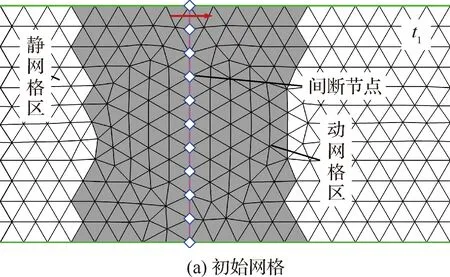
圖4 間斷附近局部網格自動重構(n=5)

3) 每次完成網格重構后，由于舊網格變形區已經不太適合新的間斷位置，因此需要重新標記動網格區和靜網格區，如圖4(d)所示，即計算過程中流場網格重構區是動態變化的，隨間斷移動需要動態調整。

2 驗證算例

本節通過3個二維算例對若干改進的準確性、可行性和可靠性做了驗證，體現了該非定常激波裝配算法在處理運動激波的潛力。值得強調的是，以下所有裝配算例整個計算完全自動進行，沒有經過任何人為干預。

2.1 激波繞射90°拐角

平面運動激波繞射尖銳拐角是一類相當常見的氣動問題，許多學者從試驗和數值的角度出發，對90°拐角的激波繞射問題做了大量研究[22-24]。根據入射運動激波的強弱，該問題主要分為兩類，即激波下游的流場是超聲速或亞聲速。圖5給出了強激波繞射下該流場的若干主要波系結構，流場在演化中具有明顯的自相似性和準定常特性。

圖5 強激波繞射90°拐角流場結構[22]

本節考慮一道平直入射激波(運動激波馬赫數Mas=2.4)繞射90°拐角的情況，初始流場參數詳見表1，流場計算區域如圖6所示，初始激波位于拐角前0.5L處，網格尺度Δ=0.25L，全場初始共有28 762個均勻分布的三角形網格單元。本算例中的時間均為無量綱量，計算中只對入射強激波進行裝配，流場演化產生的新激波仍然用捕捉法計算。

表1 激波繞射初始流場條件

圖6直觀地給出了一系列裝配得到的運動激波陣面，無量綱間隔時間dt=0.05。可以看出當入射強激波繞過壁面拐角后，激波會逐漸向垂直壁面彎曲，這是由于拐角附近的流場在膨脹波干擾下，激波強度減弱，激波運動速度降低；此外，通過觀察可以發現，相比流場上方未受干擾的入射激波，彎向垂直壁面的激波間距明顯減小，經推算此處的激波馬赫數約降為1.36。

圖6 不同時刻下繞射激波的裝配陣面

由于該算例的激波陣面在傳播過程發生了劇烈地彎曲和伸長，因此需要頻繁進行間斷節點的分布重構。從某一時刻流場出發，考察了一段時間后是否進行間斷節點分布重構的流場網格，結果對比如圖7所示。其中，左圖未進行間斷節點重構，且采用傳統的全局網格變形策略，可以發現局部間斷面元被過度拉長或擠短，不能較好地描述間斷曲率；同時激波下游網格尺度將逐漸增大，會降低此處復雜流場的解析精度。相反，算法改進后，經過若干次網格重構，間斷陣面及其附近的網格尺度和鄰近網格始終保證接近，且間斷的形狀更加光滑合理，充分反映了1.3節改進策略的必要性和有效性。

為了定性說明裝配結果的準確性，基于相同網格尺度用激波捕捉法重新計算了該問題。圖8給出了2個無量綱時刻流場密度等值線的對比(ρ0為初始入射激波上游密度)，由于捕捉激波本質上存在的數值誤差，捕捉法計算的密度等值線(白色實線)會出現兩條不合理的波帶，嚴重降低了流場等值線的光滑性；而裝配計算的等值線(黑色實線)光滑合理，沒有出現誤差帶，整體看來裝配法的流場結果更加準確可信。

圖8 不同時刻流場密度云圖對比

圖9對比了裝配法和捕捉法計算終止時刻流場壓強云圖(p0為初始入射激波上游壓強)，可以看到兩者的激波位置和大部分區域的等值線符合得較好。進一步提取x=1.6L直線上的數據，定量比較兩者壓強分布，如圖10所示，裝配法避免了捕捉法處理激波產生的虛假數值過渡區，而在膨脹波區兩者吻合很好。以上說明了對于非定常流場，裝配法即使經歷了多次網格重構和流場信息插值，仍能保持較高的計算精度。

圖9 t=0.8時刻流場壓強云圖對比

圖10 x=1.6L處壓強分布對比

2.2 二維激波管內激波增強

本節模擬二維激波管內激波增強問題。計算模型如圖11所示，通過設計特定的上下壁面收縮型線[25]，初始平面運動激波依次經過光滑的凹形曲線段、斜直線段和光滑的凸形曲線段，先后受到壁面產生的“激波-壓縮”和“激波-膨脹”擾動，形狀不斷發生改變，最終在收縮段出口恢復為增強的平面激波，且激波波面上沒有明顯擾動。

圖11 收縮壁面型線設計示意圖[25]

該激波管收縮段入口高度H0=70 mm，出口高度H1=8 mm，匯集角θ=20°；收縮段總長179.4 mm，其中凹曲壁、斜直壁和凸曲壁的水平長度分別為139.8、18.1、21.5 mm。仿真計算時，初始入射激波(Mas=3.2)位于收縮段入口前方8 mm處，激波上游為靜止空氣，且上游壓強p0和密度ρ0分別為6 kPa和0.072 855 kg/m3。采用激波裝配法計算時，全場網格尺寸ΔLSF=1 mm，一共有25 082個均勻分布的三角形網格單元。

在整個過程中，激波一共運動了170 μs。圖12依次給出了間隔10 μs裝配的激波陣面。可以清晰直觀地看到，平面激波在進入收縮段后開始逐漸自底部向中心彎曲，在斜直壁段時曲率保持不變，當傳播到凸曲壁時，激波陣面曲率逐漸減小，最終在出口位置再次轉變為平面激波。從收縮段入口運動到出口，激波長度明顯縮小，采用1.3.2節所述的間斷節點自動分布重構技術，激波陣面上的間斷節點從初始71個逐漸減少到12個。根據160～170 μs時段中激波的水平運動16.4 mm，近似求出收縮段出口位置的激波馬赫數為4.83，與試驗紋影[25]推算出的激波馬赫數4.80吻合得非常好，相對偏差僅有0.6%。

圖12 激波管內不同時刻裝配激波陣面

文獻[26]理論分析了激波運動到不同水平位置的強度，即運動激波馬赫數Mas，考慮到裝配法需要計算出間斷節點的運動速度，進而很方便地推導出激波運動馬赫數，因此本文就該數值進行對比，結果如圖13所示。可以看出，在凹曲壁段，裝配結果和理論預測符合得很好，而在斜直壁段和凸曲壁段，二者略有差別，有待進一步校核；中軸線附近的激波強度在x<80 mm段基本沒變化，受到壓縮波作用之后迅速增強，且在斜直壁段與理論預測出的壁面激波強度較為吻合，同樣，在靠近出口處，受膨脹波的影響強度有所下降。總之，采用激波裝配法可以很容易得到激波在傳播過程中的強度變化，而激波捕捉法很難直接得到，這也是裝配法的一個優勢所在。

圖14依次對比了激波捕捉法和裝配法模擬的密度ρ、壓強p和熵S=p/ργ的云圖，圖中S0為初始入射激波上游熵值。捕捉法的流場網格尺度ΔLSC=ΔLSF/5，全場共有626 128個三角形網格單元，即網格單元總量約是裝配法的25倍。對比密度和壓強云圖可以發現，捕捉法得到的等值線在x=30，130 mm左右存在明顯的振蕩，而裝配法得到的等值線光滑合理沒有波動；從熵云圖可以大致看出造成捕捉法出現非物理波動的原因，捕捉得到的激波下游會出現一條逐漸遠離激波的熵帶，一定程度污染了下游流場，這可能是由捕捉激波從本質上產生的數值誤差造成的，文獻[12,15]在計算靜止激波與渦的相互作用中也同樣發現這種現象，此處有待進一步探討。相比之下，裝配法由于精確處理了激波，即使用很少的網格也能得到較好的流場。

圖13 激波在不同水平位置的強度對比

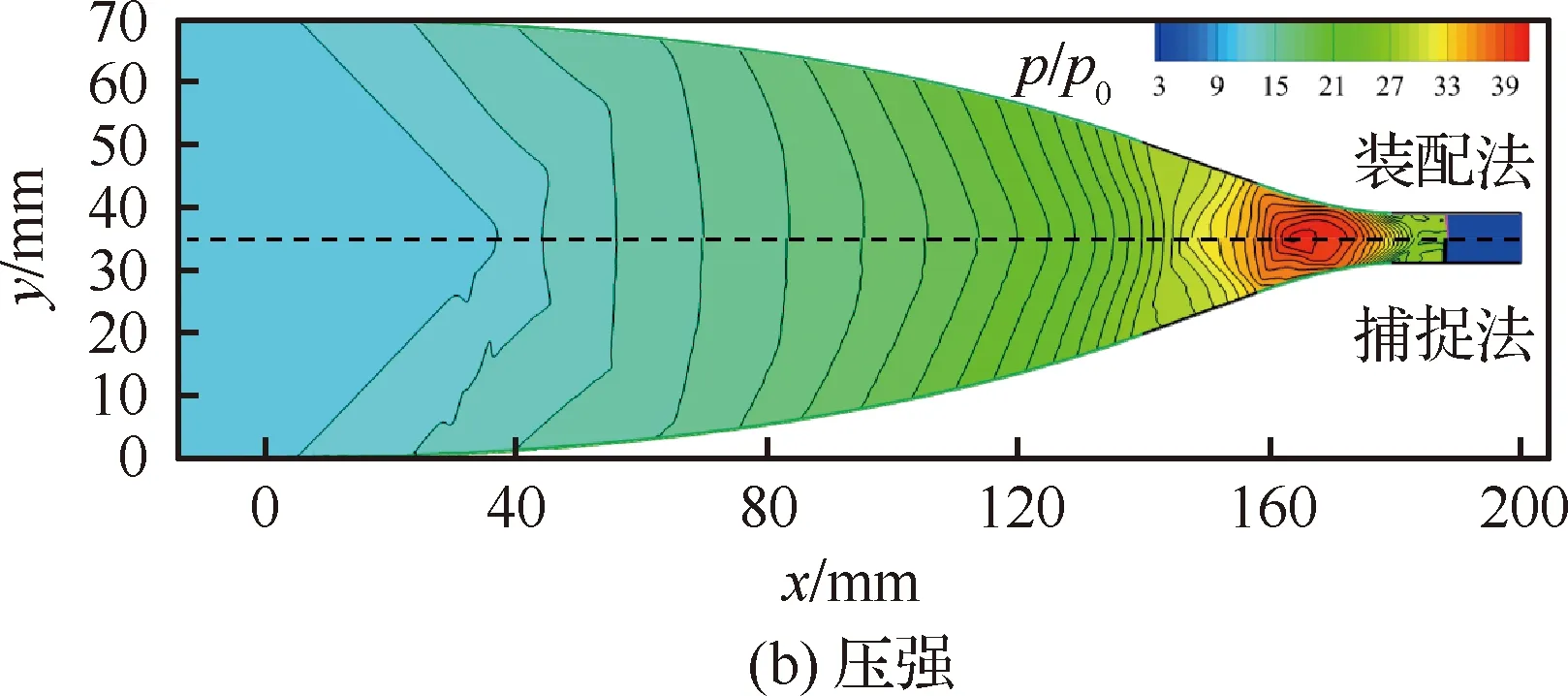
圖14 t=165 μs時刻裝配法和捕捉法模擬的流場對比

2.3 彎管內激波傳播

圖15 激波在彎管中傳播的試驗陰影圖[27]

爆震發動機中經常會出現激波在彎曲管道中的傳播現象，其典型波系結構如圖15試驗陰影圖[27]所示。本節采用激波裝配法模擬激波在“L”形彎管內的傳播、加速過程，進一步考核本方法的可靠性。

計算模型由直管段和“L”形彎管段組成，如圖16所示，內徑均為L，且彎管段的內壁面曲率半徑r=0.5L。初始入射激波馬赫數Mas=4.0，下游與上游的壓強比和密度比分別為18.5、4.571；且初始入射激波上游為靜止空氣，下游氣流馬赫數為1.553。全場網格尺度Δ=0.03L，初始共有11 654個均勻分布的三角形網格單元。本算例中的時間均為無量綱量。

圖16 計算區域、初始條件和網格

圖17 不同時刻下L形彎管內裝配的激波陣面

圖17給出了間隔dt=0.04裝配的激波陣面，入射激波于t=0.22時刻到達彎曲段入口，此時激波陣面仍是平整的，激波進入彎曲管道后同時受到內壁面的膨脹干擾及外壁面的壓縮干擾，使得靠近內壁面的激波逐漸減弱并發生彎曲以保持傳播方向與管道軸線一致，而靠近外壁面的激波受到壓縮波的作用而逐漸增強最終形成馬赫反射結構。圖中可以清晰地看到馬赫桿隨著激波的傳播逐漸變長，即三波點逐漸向內壁面移動；且從間距可以看出馬赫桿的強度更高，運動速度更快。

非定常流動中三波點等間斷相交點運動速度的求解一直以來是個難題，目前尚未有完善的理論模型，因此運動相交點的處理是裝配法的一個研究重點。圖18給出了某時刻間斷節點運動示意，其中三波點的運動速度沒有修正，造成鄰近的間斷面元斜率出現異常，隨著時間推進，三波點位置會迅速發散引起計算失敗。

本文提出一種“預估位移，推算速度”的策略間接完成運動三波點的裝配，下面結合圖19介紹其關鍵步驟：

圖18 未修正的三波點運動

圖19 三波點運動速度計算模型

步驟1辨識三波點(TP)。分析可知三波點一般位于幾個不同斜率激波線的交匯處，如圖19所示，求解每個間斷節點左右兩個相鄰間斷線元的夾角ψ，若ψ高于某閾值ψthr，則標記該節點為三波點。數值試驗表明ψthr通常取15°即可。

步驟2求解相交點新時刻位置。首先根據1.2.3節求得的間斷節點運動速度，分別計算三波點TP左鄰居間斷節點(P1～P3)和右鄰居間斷節點(P4～P6)在t+Δt時刻的位置(圖19藍色實心方塊)，然后分別擬合出兩條直線(圖19黑色實線)，可以認為這兩條直線與新時刻三波點附近的激波線斜率近似一致，最后求解這兩條直線的相交點(圖19紅色實心方塊)作為新時刻三波點的位置。

步驟3計算三波點速度。由舊三波點到新三波點的位移矢量為LTP，則三波點的運動速度矢量ωTP=LTP/Δt。

值得注意的是，雖然此處針對的是三波點結構，但其他間斷相交點的運動也可以類似處理，這里不再詳述。

為了校核本算例三波點位置計算的準確性，圖20對比了任意兩個時刻捕捉法和裝配法的結果，可見裝配的入射激波、馬赫桿和三波點位置和捕捉結果基本吻合。此外，對比圖20和圖16的流場網格，可見裝配激波走過的區域，經1.3.3節所述的網格重構策略，流場網格可以恢復到初始高質量網格，很好地減弱了裝配陣面對流場網格的影響。

圖20 不同時刻流場密度云圖及網格對比

3 結 論

本文面向非定常流動中激波傳播問題，對最近發展的自適應間斷裝配求解器ADFs進行了若干改進，主要結論如下：

1) 當激波在曲壁面上運動時，運動間斷節點可以在固定壁面網格節點的前提下實現裝配。

2) 針對激波產生大變形、大位移運動問題，通過間斷節點分布的自動重構保證激波陣面不失真，同時采用局部網格自動重構策略確保了網格的高質量，并提高了程序計算效率。

3) 對于激波相交點的運動，設計了一種根據位移推算速度的方法進行裝配，數值算例表明該方法行之有效。

總之，采用激波裝配法處理激波傳播問題，相比激波捕捉方法可以獲得流場間斷更加直觀清晰的圖譜，有利于進一步深入認識激波的演化過程。本文僅對單個運動激波進行裝配，流場演化中的新生激波仍用捕捉法進行處理，而激波裝配法的目標是顯式地自動模擬這些間斷拓撲變化問題，因此將激波辨識技術融合到激波裝配法中將是下一步工作的重點。

致 謝

中國科學技術大學的楊基明老師在激波增強管壁型線幾何模型方面給予了協助和寶貴的指導，在此致以衷心的感謝!