存在同軸度誤差的徑向永磁聯軸器傳動特性分析*

田 杰，趙曉聰

(合肥工業大學 機械工程學院，安徽 合肥 230000)

0 引 言

隨著銣鐵硼永磁材料的廣泛應用，永磁聯軸器在近些年來得到了空前的發展，永磁聯軸器具有對動力源隔離振動、過載保護、能夠實現軟起動、裝配維修拆卸方便等優點，現已廣泛應用到礦山機械、風力傳動以及危險介質傳動等場合[1]。

由于其在工程應用中具有非常好的應用前景，國內外關于永磁聯軸器的研究在近年來也在不斷推進，國外對于永磁聯軸器的理論研究體系比較完善，從結構設計到參數優化，從仿真分析到實驗探索都已經形成一套比較系統的研究體系[2-4]；國內由于研究起步較晚，目前對于永磁聯軸器的研究主要集中在磁場分布、結構優化、機械特性的計算[5-7]，而對于永磁聯軸器在實際工程應用由于制造或安裝誤差帶來的傳動不平穩問題國內外還沒有系統的理論和方法來進行研究和分析。

徑向永磁聯軸器結構示意如圖1所示。

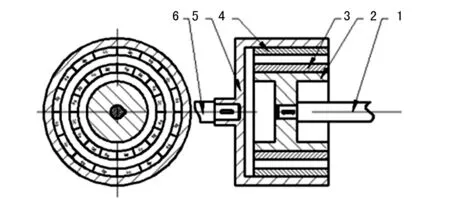
圖1 同步式徑向永磁聯軸器結構示意圖1.主動軸 2.內轉子 3.永磁體 4.永磁體 5.外轉子 6.從動軸

其主從動轉子上的永磁體采用軸向充磁，主動轉子隨著主動軸旋轉時，永磁體間產生相對轉角，從動轉子受到磁力作用帶動輸出軸轉動。由于徑向永磁聯軸器主從動轉子不接觸，在制造和安裝過程中徑向永磁聯軸器主從動轉子間易產生一定的不對中誤差，從而引起傳動不平穩、效率降低、軸心大幅度振動等問題，甚至導致結構的破壞[8]。因此，研究此類永磁聯軸器同軸度誤差下的轉矩特性對于徑向永磁聯軸器系統的安裝調整、結構優化、參數設定等方面具有重要的實用價值。

1 磁場分析

研究同軸度誤差對徑向永磁聯軸器轉矩特性的影響，首先需要對存在誤差的系統進行磁場分析，研究誤差對磁場分布的影響以此初步分析系統是否滿足傳動要求。由于徑向永磁聯軸器結構的對稱性，可以采取軸心截面進行二維磁場分析。

根據參考文獻[9]，取徑向聯軸器兩磁環的材料參數和幾何尺寸如表1所列。以外磁環軸線為中心，將內磁環沿豎直方向偏移，設置同軸度誤差分別為0 mm、1 mm、3 mm、5 mm。

表1 磁環材料參數及尺寸參數

在Ansoft Maxwell 2D中構建二維模型，根據磁極的矯頑力和剩磁參數設置永磁材料，將外部空氣設置為Vector Potential邊界。采用基于模型內部單元邊長進行模型網格劃分，長度設置為1 mm。設置求解器后啟動求解。根據仿真結果可得二維磁場分布如圖2所示。

根據圖2中分析結果可看出，當同軸度誤差為0 mm時，磁力線和磁場強度都是對稱分布，徑向永磁聯軸器正常運轉；隨著同軸度誤差的逐漸增大，系統磁場分布逐漸出現不對稱不均勻的現象，導致系統出現傳動不穩定的情況；當同軸度誤差達到5 mm時，從磁場分布圖2(d)中可以看到磁力線出現明顯的疏密區別，上、下部分磁力線密度數值出現較大偏差，聯軸器系統無法保證正常傳動，故安裝和制造過程中的同軸度誤差對系統穩定傳動會產生很大的影響，需要對其進行進一步定量分析計算。

圖2 不同同軸度誤差下的磁場分布圖

2 傳遞轉矩理論計算

磁荷庫倫定律作為等效磁荷計算法的核心理論，其基本思想是計算空間內兩微小固定點磁荷之間的作用力。對于徑向永磁聯軸器而言，將聯軸器內的永磁體磁化表面等效為若干個磁荷微單元，進而得出兩任意位置永磁體之間的磁力[10]。故同軸度誤差下徑向永磁聯軸器結構可簡化得以下計算模型，并以外磁環軸線方向建立x軸，以豎直方向建立z軸，構建笛卡爾空間直角坐標系Oxyz，如圖3所示，假定內外兩個永磁體磁環軸線相互平行無角度偏移且磁化方向相同。

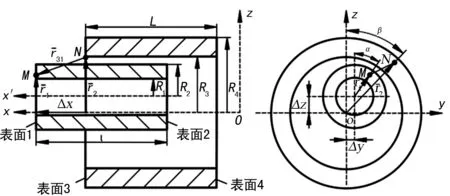
圖3 轉矩計算模型

記M點是內磁環磁極表面1上任意點，則點M處的微元磁荷可表述為：

qm=σ1r1dr1dα

同理外磁環磁極表面3上任意點N微元磁荷可表述為：

qn=σ2r2dr2dβ

式中：r1為內磁環磁極表面任意點極長；r2為外磁環磁極表面任意點極長；σ1、σ2分別為內外磁環磁極表面的磁荷面密。

根據磁極化強度與磁荷面密度之間的關系式σ=Br·n(n為磁極表面的法線方向)，當磁極化強度垂直于磁體表面時：

σ1=σ2=Br

基于磁荷庫倫定律在同軸磁環內的推導公式，則兩磁環的相應磁極表面1和3上任意兩點之間的微元磁力為：

(1)

其中1、3磁極表面兩微元磁荷的向量模長|r31|為：

式中：l為磁環軸向長度；Δx為軸向誤差，Δy、Δz為徑向誤差(假定三個誤差值分別沿坐標軸正向)；r31為1、3面任意兩點之間的空間向量；r1為內磁環的內徑；r2為內磁環的外徑；r3為外磁環的內徑；r4為外磁環的外徑。

微元磁力分解到三個坐標軸的分力為：

(2)

(r1sinα+Δy-r2sinβ)

(3)

(4)

同理可以得到聯軸器其余磁極面之間的向量關系，將向量投影到各坐標軸長度如表2所列。

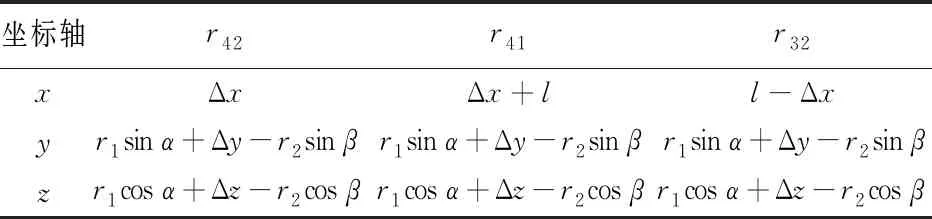
表2 其他向量在各坐標軸投影長度

表中r42表示4、2磁極表面兩微元磁荷的向量模長；r41表示4、1磁極表面兩微元磁荷的向量模長；r32表示3、2磁極表面兩微元磁荷的向量模長。

磁力聯軸器的傳遞轉矩為各微元分力對x軸的轉矩，如下表達式所示：

dT31x=dF31y(Δz+r1cosα)

+dF31z(r1sinα+Δy)

(5)

dT32x=dF32y(Δz+r1cosα)

研究組患者治療后經胃鏡檢查結果痊愈率為88.33%，與對照組（68.33%）比較，研究組治愈率高于對照組，組間比較，差異具有統計學意義（P＜0.05），詳情見表2 。

+dF32z(r1sinα+Δy)

(6)

dT41x=dF41y(Δz+r1cosα)

+dF41z(r1sinα+Δy)

(7)

故聯軸器系統對x軸的磁力轉矩為：

dTx=dT31x+dT42x+dT41x+dT32x

[(r2sinβ-r1sinα-Δy)(Δz+r1cosα)+

(Δz+r1cosα-r2cosβ)(Δy+r1sinα)]×

r1r2dr1dr2dαdβ

(8)

對公式(8)積分可得到內外磁環之間磁力矩為：

[(r2sinβ-r1sinα-Δy)(Δz+r1cosα)+

(Δz+r1cosα-r2cosβ)(Δy+r1sinα)]×

r1r2dr1dr2dαdβ

(9)

3 轉矩公式的仿真驗證

公式(9)即為徑向永磁聯軸器在同軸度誤差下的傳遞轉矩計算公式。為驗證公式正確性，利用Ansoft Maxwell仿真得出不同誤差值下的傳遞轉矩數值，與利用Matlab求解公式(9)所得傳遞轉矩數值進行比對。

利用表1中數據建立不同安裝誤差下徑向永磁聯軸器三維模型，在Ansoft Maxwell 3D中構建三維模型，根據表1中矯頑力和剩磁參數設置永磁材料，將外部空氣設置為Zero Tangential H Field邊界。采用軟件自帶的自適應網格劃分。設置力矩求解器后啟動求解。

最后進行三維瞬態磁場分析計算，得出聯軸器工作過程中的穩定傳動轉矩，將相同誤差下磁場仿真值并與公式計算值進行對比，如表3所列。

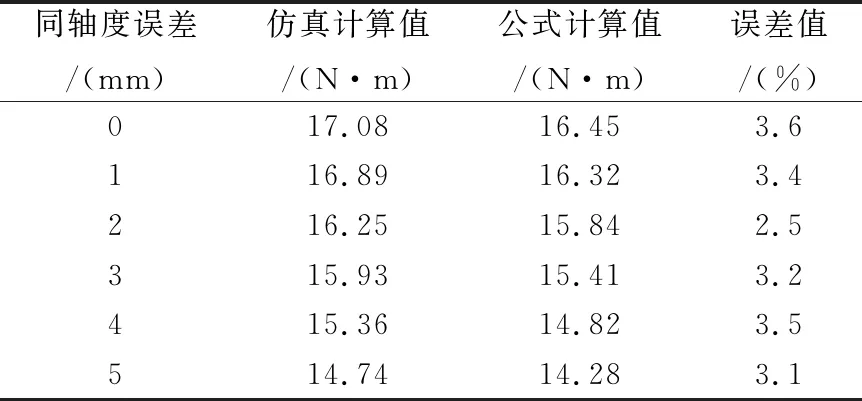
表3 轉矩公式仿真驗證對照表

從表3驗證計算結果可以看出，公式計算結果與仿真值的誤差保持在5%以內，證明所推導的公式具有很高的可行性，能夠相對準確快速地計算出徑向永磁聯軸器存在安裝誤差下的傳遞轉矩，可以為徑向永磁聯軸器的誤差分析提供可靠的理論依據。

4 存在同軸度誤差時轉矩特性分析

傳遞轉矩是徑向永磁聯軸器傳動特性的關鍵衡量參數，通常在設計時通過改變表1所示的徑向永磁聯軸器的永磁體厚度，或調節主從動轉子間徑向氣隙實現工作所要求的傳遞轉矩，本節針對不同結構參數研究同軸度誤差對傳遞轉矩的影響，從而得出為保證各參數尺寸的聯軸器系統可實現正常傳動時的安裝精度。

4.1 不同永磁體厚度下同軸度誤差對傳遞轉矩影響

永磁體徑向厚度增加時其儲存的磁能會增加，徑向永磁聯軸器的傳動性能進一步提高，但會導致其制造成本的升高。因此一般在設計過程中遵循滿足傳動要求的最低成本化要求。保持聯軸器系統其他結構參數不變，同時改變內轉子的內徑及外轉子外徑獲得不同的內、外轉子厚度。利用公式(9)計算得出各同軸度誤差下永磁體厚度變化量為Δ時所對應的傳遞轉矩，所得數據見表4所列，并利用Matlab作出相應的變化曲線如圖4所示。

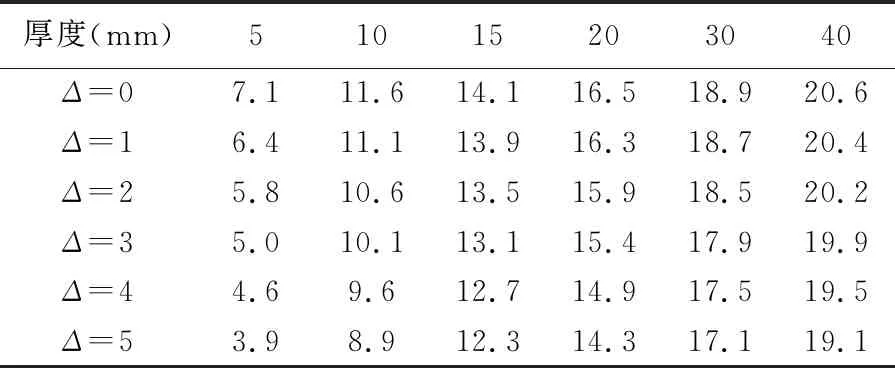
表4 同軸度誤差下聯軸器在磁體厚度變化下傳遞轉矩 /N·m

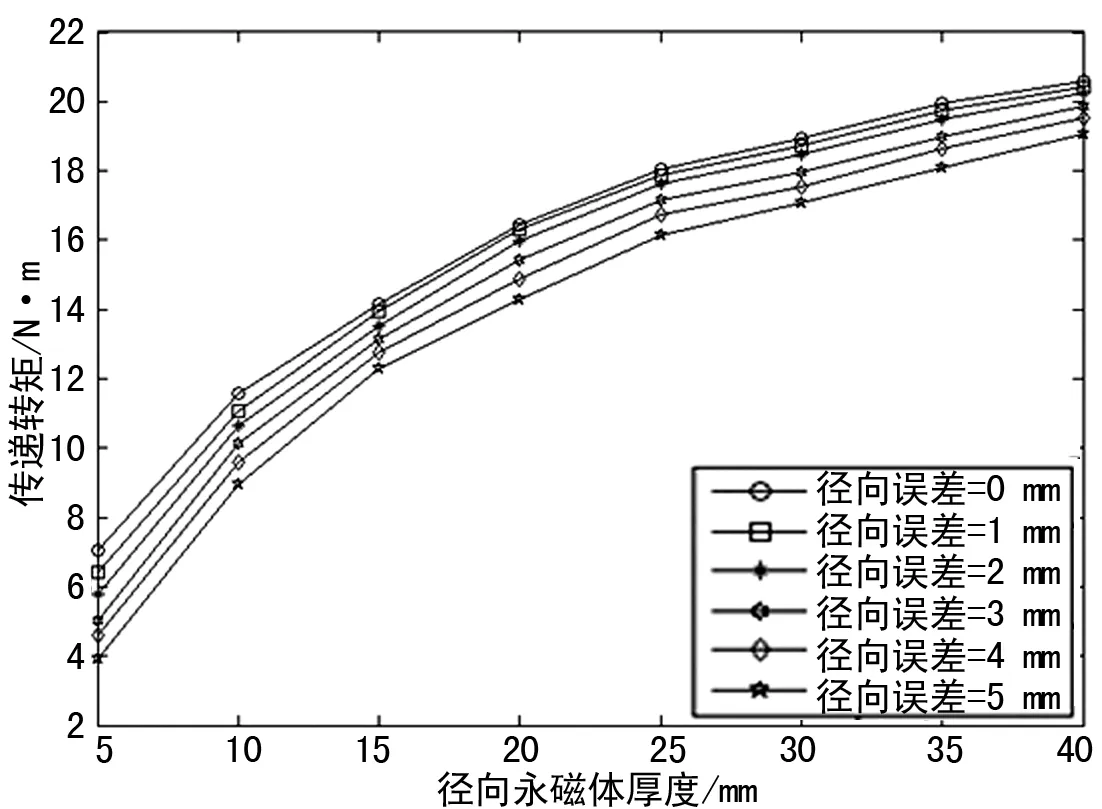
圖4 不同磁體厚度下同軸度誤差與傳遞轉矩關系

從表4中數據和圖4的變化趨勢可以看出：隨著永磁體徑向厚度的增加，永磁體之間的作用力逐漸變大，即永磁聯軸器的傳遞轉矩越大，同軸度誤差對聯軸器系統的傳遞特性影響會逐漸降低。為了保證徑向永磁聯軸器傳動的穩定性和高效性，即保證徑向永磁聯軸器在實際工作時的傳遞轉矩可以達到原本設計時傳遞轉矩的90%，進而推薦永磁體厚度尺寸為10 mm以下的徑向永磁聯軸器同軸度誤差應保證在1 mm以內；同理，永磁體厚度為10～20 mm的徑向永磁聯軸器同軸度誤差應保證在2 mm以內，永磁體厚度超過20 mm的徑向永磁聯軸器同軸度誤差應保證在3 mm以內。

4.2 不同徑向氣隙下同軸度誤差對傳遞轉矩的影響

氣隙是指在內外磁環之間的徑向空氣間隙，本節在分析不同氣隙下同軸度誤差對傳遞轉矩影響時，通過將內永磁體磁環固定，改變外磁環尺寸達到改變徑向氣隙的大小。整個分析過程中外磁環尺寸增大會導致永磁體體積也進一步增大，所儲存的磁能也進一步增大，過程中存在氣隙和永磁體體積兩個變量從而具有一定的局限性，相關計算分析對安裝精度標準化有著相當可觀的參考價值。計算得出各同軸度誤差下內外磁環氣隙變化量為Δ時所對應的傳遞轉矩，所得轉矩數據見表5所列，作出相應的變化曲線如圖5所示。

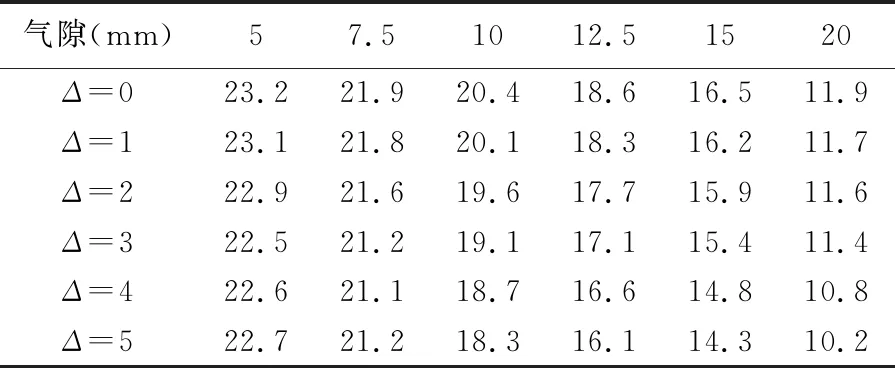
表5 同軸度誤差下聯軸器在氣隙變化下的傳遞轉矩 /N·m

圖5 不同磁環氣隙下同軸度誤差與傳遞轉矩關系

從表5中數據和圖5的變化趨勢可以看出：隨著徑向氣隙的增大，徑向永磁聯軸器的傳遞轉矩會逐漸降低；當內外磁環徑向氣隙較小時，同軸度誤差對系統傳遞轉矩的影響較小，但工作過程中當存在較大誤差時較小的徑向間隙很可能會導致主從動轉子在產生振動的過程中發生碰撞；當內外磁環徑向氣隙逐漸增大時，同軸度誤差對系統傳遞轉矩影響逐漸增大。為了保證系統傳動的穩定性和安全性，進而推薦內外磁環徑向間隙為10 mm以下的徑向永磁聯軸器同軸度誤差應保證在1 mm以內；同理，內外磁環徑向間隙為10～15 mm范圍的徑向永磁聯軸器同軸度誤差應保證在2 mm以內，內外磁環徑向間隙超過15 mm的徑向永磁聯軸器同軸度誤差應保證在3 mm以內。

5 結 論

(1) 利用磁荷庫倫定律推導得出同軸度誤差下的徑向永磁聯軸器轉矩計算公式，并通過數值計算和仿真驗證對比驗證了其正確性，從而可以應用到徑向永磁聯軸器的產品設計和同軸度誤差標準化過程中。為徑向永磁聯軸器系統的安裝調整、結構優化提供理論依據。

(2) 針對目前應用最為廣泛的兩類徑向永磁聯軸器，即永磁體厚度變化系列和徑向氣隙變化系列，利用公式計算得到聯軸器正常傳動所必須保證的同軸度安裝精度，整個計算過程利用Matlab編程簡單且準確率較高。

(3) 從磁場分析結果著手，利用等效磁荷法建立數學模型進行轉矩計算的研究方法，可應用到其他類型磁力聯軸器的結構設計和安裝精度標準化過程。