妙用復數性質巧解題

■甘肅省白銀市第一中學

復數是高考必考的知識點,著重考查其概念及運算。靈活運用復數性質,便可達到化繁為簡,化難為易的效果,下面通過近幾年高考題,來說明復數性質的應用。

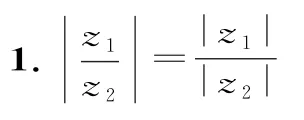
例1(2019新課標Ⅰ卷文數)設z=,則|z|=( )。

練習1.(2019年天津卷文數)設i是虛數單位,則

2.|z1·z2|=|z1|·|z2|

例2(2017年江蘇卷理數)已知復數z=(1+i)(1+2i),其中i是虛數單位,則z的模是_____。

解法1：(常規法)因為z=(1+i)(1+2i)=1+2i+i-2=-1+3i,所以|z|=

解法2：(性質法)|z|=|(1+i)(1+2i)|=|1+i||1+2i|=

練習2.(2017年全國新課標Ⅲ卷理數)設復數z滿足(1+i)z=2i,則|z|=( )。

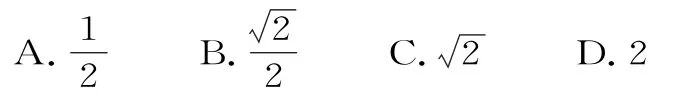
答案：C。

3.|z|2=a2+b2=(a+bi)(a-bi)

例3(2019年新課標Ⅲ卷理數)若z(1+i)=2i,則z=( )。

A.-1-i B.-1+i

C.1-i D.1+i

解法1：(常規法)由z(1+i)=2i,得z=答案為D。

解法2：(性質法)由z(1+i)=2i,得z(1+i)=(12+12)i。所以z(1+i)=(1-i2)i,z=(1-i)i,即z=1+i。答案為D。

練習3.(2018年浙江卷)復數(i為虛數單位)的共軛復數是( )。

A.1+i B.1-i

C.-1+i D.-1-i

答案：B。_

4.|z|2=

例4(2019年北京卷理數)已知復數z=2+i,則

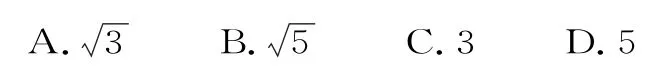
解法1：(常規法)因為z=2+i,所以z·故選D。

解法2：(性質法)因為z=2+i,所以z·故選D。

練習4.(2016年全國Ⅲ卷理數)若z=1+2i,則

A.1 B.-1 C.i D.-i

答案：C。

5.a+bi=(b-ai)i

例5(2016年北京卷文數)復數=( )。

A.i B.1+i C.-i D.1-i

練習5.(2015年天津卷文數)i是虛數單位,則

答案：-i。

6.(1±i)2=±2i

例6(2015年湖南卷)已知1+i(i為虛數單位),則復數z=( )。

A.1+i B.1-i

C.-1+i D.-1-i

練習6.(2015年廣東卷文數)已知i是虛數單位,則復數(1+i)2=( )。

A.-2 B.2

C.-2i D.2i

答案：D。

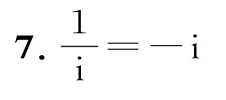
例7(2015年四川卷理數)設i是虛數單位,則復數

A.-i B.-3i C.i D.3i

解法1：(常規法)i3-+2i=i。故選C。

解法2：(性質法)i3--i+2i=i。故選C。

練習7.(2015年四川卷文數)設i是虛數單位,則復數

答案：2i。

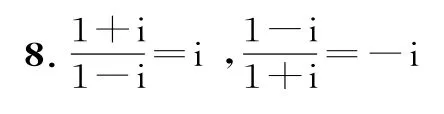
例8(2014年全國新課標Ⅰ卷理數)

A.1+i B.1-i

C.-1+i D.-1-i

練習8.(2014年湖北卷)i為虛數單位,則

A.1 B.-1 C.i D.-i

答案：B。

復數運算問題多是基礎題,按照常規的通性通法去解決,難度不大,靈活運用性質巧解,更加便捷!