一個“增解”問題的根源剖析與思考

安徽省臨泉第一中學 (236400) 張翠蘭

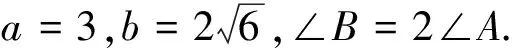
(Ⅰ)求cosA的值；

(Ⅱ)求c的值.

有高三備考資料中，關于此題給出的參考答案如下(不妨稱解法1)：

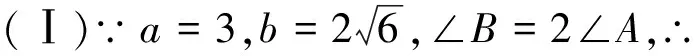
(Ⅱ)由余弦定理a2=b2+c2-2bccosA，得

一、問題

這道題不僅題型比較常規，而且解答思路也常規，容易上手，不少學生也能想到上述求解思路的，但有一點卻不易使大家想到，就是第(Ⅱ)問的解答中在利用余弦定理求出c=3或c=5之后，就認為求解結束了，已經萬事大吉了，根本想不到還需檢驗c=3是否符合題意，從而就會造成因“增解”而導致錯誤發生.當然，檢驗c=3或c=5是否符合題意，也不是難事，對于我們來說，難在想不到“第(Ⅱ)問的最后解答還需檢驗”這一環節，這一盲點現象為何比較普遍呢？是什么導致增解呢？

二、剖析

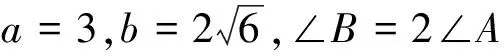
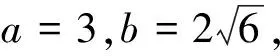
三、思考

筆者也向同事們詢問他們對于上述解法“驗證”的觀點，有的教師對學生說：“此題是高考解答題的第(Ⅰ)題，第(Ⅱ)題不可能平鋪直敘，一點彎彎沒有,否則，太簡單了，索然無味，既然解答出現了兩個結果，最好驗證一下”；有的教師對學生說：“第(Ⅱ)問是屬于‘知道三角形的兩邊及其中一邊的對角’求解三角形的問題，雖然利用余弦定理求解的，但余弦定理不能保證三角形存在，故需檢驗求解的結果.”筆者認為對于上述解答的“驗證”原因持這兩種觀點的教師不少，因為找不到產生“增解”的根源，只好自圓其說，糊弄學生.其實，這兩種觀點都是錯誤的，缺乏理性思維，是認識問題膚淺的表現，顯然觀點1是無稽之談，觀點2是對余弦定理隱含著保證“三角形的存在性”這一功能的認識.

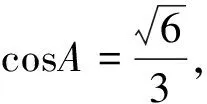
事實上，本題第(Ⅱ)問，還有其它更好解法，下面再提供兩種解法：

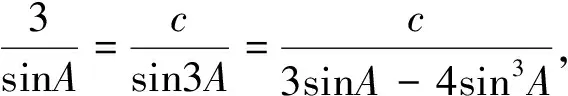
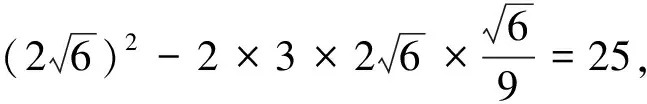
通過以上思考，可以看出教師只有將問題講透，學生才能學得明白，學得輕松，從而才能激發學生學習數學的熱情與興趣，然而如何才能做到把數學問題講透？特別是學生感到困惑的問題，這也是困擾我們一線教師的難題，其實，有不少數學問題的解決方案，我們教師也稀里糊涂的，只不過是“身經百戰”，見多了，其解法都爛熟于心了，教學中一旦遇到它們，就直接將熟知的解法拋給學生，而不是通過引導學生分析題目條件與結論以幫助學生形成解題思路，可謂告訴的多，分析的少，究竟為什么這樣做而不那樣做的想法，則不舍得花費時間分析，所以一旦學生問到：“老師，這個解法，您怎么想到的？”之類的話題，教師往往啞口無言，不清楚為何，因為平時對“為什么這樣做”思考得少，自己就昏昏然，怎能使人昭昭？難怪不少教師發出感嘆：這道題都講幾遍了，學生仍然不會.筆者認為出現這種現象之所以比較普遍，是因為我們教師沒有將問題講明白，感動不了學生，引發不了學生心理的震撼，并不是說我們教師天天重復講，學生就能學會數學的，因為不理解的問題是難以接受的，更談不上融會貫通及靈活運用了.

因此，作為教師我們如果自己能被數學感到了，教師才能自覺地、不失時機地用數學的魅力去打動學生，試想：我們數學教師面對一個數學問題的解決過程，自己就感動不了，怎么能感動學生呢？