好問題，成就好課堂*
——蘇教版四年級下冊《平移》一課的研究與實踐

□吳文娟 俞昭英

一堂好課得益于好的問題，好問題能引導學生深入思考，能揭示知識的本質，更能促進學生數學素養的提升。筆者一直在思考設計怎樣的好問題，以此來引領課堂教學，蘇教版四年級下冊《平移》一課的實踐使筆者獲得了一些啟示。

【教學片段1】

（多媒體演示幾個圖形的運動，如圖1）

師：這些圖形是以什么方式運動的？（學生一一回答）

師：平移和旋轉是圖形運動的兩種基本方式，三年級時我們就已初步認識了。

師（出示其中三個平移的圖形，如圖2）：請仔細觀察，這三個圖形的運動都是平移，但有什么不同嗎？

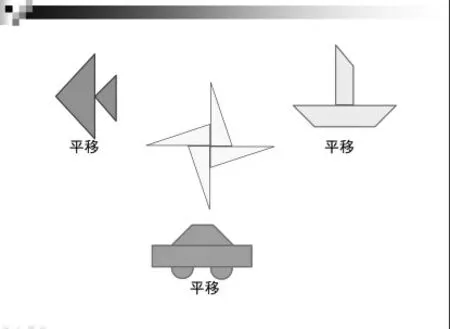
圖1

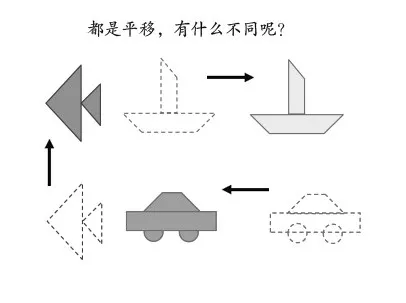
圖2

生：它們有的向上平移，有的向左平移，有的向右平移。

生：它們平移的方向不同。

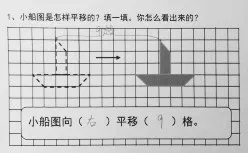
師（出示小船向右平移的兩個圖形，如圖3）：同樣是把小船圖向右平移，有什么不同嗎？

生：它們平移的距離不同。

師：如果要說一說小船圖是怎樣平移的，你覺得要說清楚哪些要素？

生：要說清楚它向哪個方向平移，平移了多少距離。

（師即時板書：“距離”“方向”）

（思考：距離和方向是平移的兩個基本要素，也是描述物體平移時必須要準確表述的內容。教學時筆者先讓學生判斷圖形的運動方式，激活他們已有的知識經驗。在此基礎上，學生通過兩次“異中求同”的比較得出平移的兩個要素。）

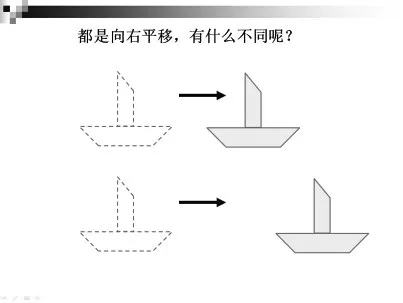
圖3

【教學片段2】

（多媒體演示小船圖在沒有格子的平面上平移）

師：你能說說小船圖是怎樣平移的？

生：小船圖是向右平移了一段距離。

（師出示格子圖）

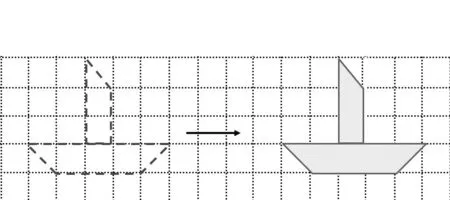
說一說：小船圖是怎樣平移的？

師：現在你能說說小船圖是向右平移了多少格嗎？看圖想一想，可以在圖上做一些標記。

（生嘗試數出小船圖平移的距離。交流時說小船圖向右平移4 格、5 格、8 格、9 格、10 格的學生都有）

師：小船圖到底向右平移了幾格呢？怎樣檢驗出正確答案呢？

生：我們剪個小船來移一移，一邊移一邊數。

生：老師用電腦再演示一遍，我們來數一數。

（生用事先剪好的小船圖移一移，師用電腦演示小船圖一格一格移動的過程，生數出小船圖向右平移了9格）

（思考：大部分學生能準確地數出小船圖平移的距離。他們對平移距離已有一種直覺經驗，所以教學中，教師可放手讓學生嘗試數出平移的距離，通過學生之間的差異來生成學習資源，促成經驗的糾錯或提升。）

師：數對的同學誰愿意與大家分享一下自己的數法？

生：我是數了小船船帆頂上的那個點平移前后之間的格子數。

生：我是數了原來的小船和平移后的小船尾部那個點之間的格子數。

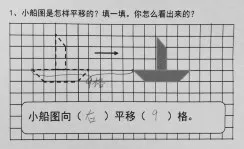
生：我是數了船帆右邊那根豎線之間的格子數。

……

師：哦，雖然他們數的位置都不同，但他們找的地方有什么相同之處嗎？

生：他們都是找了小船圖平移前后一樣的地方。

師：你們真善于觀察和思考，像這樣小船圖平移前后同一個部位的點、線，我們稱之為對應點和對應邊。

師（出示數出4 格、8 格、5 格、10 格的圖）：看看，他們的數法為什么是錯的呢？

生：他們沒有找對應點來數。

師：你們還能在平移圖上找到其他的對應點或對應邊嗎？它們之間的距離是幾格？隨便找一組數數，看有什么發現嗎？

生：我發現小船圖在平移時所有對應點或對應邊之間的距離都是相等的。

師：這個相等的距離就是小船圖平移的距離。每人選小船圖上的一個點或一條邊，老師讓小船圖再移一次，你們數數是不是都平移了9格。

師：現在你知道怎樣判斷格子圖上一個圖形平移的距離了嗎？

生：只要找一組對應點或對應邊，數出它們之間的格子數就行了。

（思考：為了讓學生充分感知平移的本質，筆者讓學生觀察比較數正確同學的共同之處，明確對應點的概念；又讓學生辨析數錯同學的出錯原因，突出對應點的重要性；再讓學生發現任一組對應點之間距離相等的規律；最后，通過小船圖的移動再一次驗證對應點之間的距離處處相等。這一系列圍繞“對應點”展開的活動讓學生深刻感悟到“對應點”的重要性，從而深入領會平移的特征。）

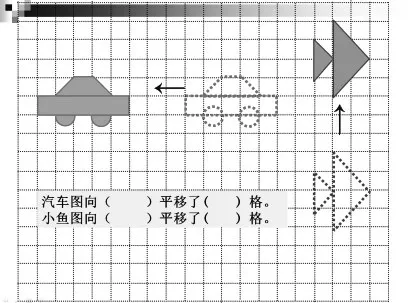
師：看看汽車圖和金魚圖是怎樣平移的？

生：汽車圖向左平移8格，金魚圖向上平移7格。

師：觀察平移前后的圖形，你有什么發現？

生：平移前后的圖形大小不變，形狀不變，但位置變了。

師：這就是平移的特征。

【教學片段3】

師：你能畫出平行四邊形向下平移3格后的圖形嗎？

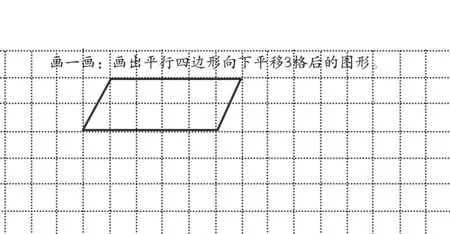
（生嘗試畫）

師：誰來把自己的畫法與大家交流交流？

生：我把平行四邊形的4 個頂點先向下平移3格畫出來，再依次連一連。

生：我把平行四邊形上面的邊向下平移3 格，再斜過1 格畫出左右兩條邊，最后連接最下面那條邊。

生：我是先平移平行四邊形左上角的一個頂點，再照著上面的圖畫出平行四邊形。

師：他們的畫法雖然各不相同，但有相同之處嗎？

生：他們都要先畫出對應點或對應邊，再連線。

師：畫圖前先直觀感知一下平移后的圖形大概在哪里，找到一組或幾組對應點或對應邊，再畫完整圖形。

師：畫得對不對，你可以怎樣檢驗？

生：看看是不是和原來的圖完全一樣。

生：可以任選一組對應點或對應邊，看看是不是向下平移3格。

（思考：為了提高學生畫平移圖形的正確率，教師通常會要求學生先平移每個對應點，再連線，但這并不是最好的方法。不同學生由于空間直覺能力的差異，會有更符合自身能力水平的畫法。筆者讓學生先嘗試畫，再交流，以此鼓勵學生運用自己的方法。這既能拓寬學生的學習思路，更是對不同學習水平學生的尊重。）

【教學啟示】

一、好的問題應該是開放的，利于學生的多維表達

教師在課堂上提的問題基本有兩種：封閉式問題或開放式問題。封閉式問題的答案是唯一的，解決方法常常也是唯一的。經常提封閉式問題，會局限學生的思維發展，不利于學生發散思維和創新思維的培養。而開放式問題可能答案不唯一，解決方法不唯一，這樣的問題更能尊重學生的不同個性和發展水平，使不同思維層次的人在相互交流、碰撞中得到不同的提升。在教學片段2 中引導學生探究向右平移的格子數時，筆者沒有像很多教師那樣設計一個點的平移、一條線段的平移、一個圖形的平移這樣有層次的三個問題，而是直接讓學生通過觀察數出小船圖向右平移的格子數。這一開放性問題，可以使學生調動已有的有關平移的經驗，借助直覺思維獲得答案。答案雖是唯一的，但數的方法卻是多樣的。這些都是很好的生成性資源，為接下來從不同方法中比較出共同點做好鋪墊。在教學片段3 中，讓學生畫出平移后的圖形，也是一個具有開放性的問題。學生可以整體感知平移，也可以先平移對應點或對應邊再連線。空間觀念強的學生也許只要平移一個點就能畫出平移后的圖形，而對于空間觀念較弱的學生也許要平移所有的點才能畫出這個圖形。開放的解決方法為不同學習能力的學生提供了達到目標的不同路徑，使不同層次的學生都能體驗到成功的喜悅。

二、好的問題應該是明確的，指向數學學習的本質

好的問題應該是明確的，這種明確并不是說給學生直接指明答案或解決路徑，而是讓學生在這個問題的引領下自己找到解決問題的方法和問題的答案。如教學片段1 中“請仔細觀察，這三個圖形的運動都是平移，但有什么不同嗎？”“同樣是把小船圖向右平移，有什么不同嗎？”這兩個問題，方法是明確的，要學生通過觀察和比較得到答案，答案也是明確的，要“異中求同”，“異”乃方法各異，而“同”則指過濾掉具體學習材料中非本質因素后沉淀的數學知識本質——平移的兩個要素：方向和距離。又如教學片段2 中，當學生交流自己的數法時，教師提問：“雖然他們數的位置都不同，但他們找的地方有什么相同之處嗎？”這一問作為開放方法后的點睛之問，使學生的思維由“發散”實現“聚合”，聚合的目的正是為了找出確定平移距離的規律——對應點和對應邊的距離即圖形平移的距離。再如教學片段3 中,學生交流各種畫法后，教師提問：“他們的畫法雖然各不相同，但有相同之處嗎？”讓學生把目光聚焦到畫平移圖形方法的本質上——對應點和對應邊的確定。在教學中我們經常會使用這類“異中求同”或“同中求異”的比較性問題，這類問題有利于學生思維發散后的聚攏，有利于學生將思考聚焦到數學學習的本質，也有利于學生思維實現從具體直觀向抽象概括的提升。

三、好的問題應該是連續的，促進思維的由淺入深

評判問題好壞的最重要的標準是看能否促進學生思考，能否促進學生思維的發展。而學生思維的發展也不是一蹴而就的，是一個螺旋上升、逐級前進、由量變到質變的過程。這就需要教師設計帶有層次性的提問來促進學生的思維由淺入深。所以好的問題不是單一的，而是連續的問題串，但這串問題中總有一個或幾個核心的問題，其他的問題均由此派生，以促進學生對核心問題的理解。學生在三年級已初步認識了物體的平移和旋轉，而四年級下冊平移這一內容的學習重點是讓學生準確描述物體的平移，會畫平移后的圖形。雖然這兩個學習重點更側重于技能的習得，但其核心都是對“對應點”的認識和平移圖形特征的認識。基于此，筆者將本課的核心問題設計為小船圖向右平移了多少格。圍繞這一問題，教學片段1通過三個連續的問題，明確了要準確描述物體的平移關鍵是說清“方向”和“距離”，而“距離”的確定又是關鍵中的難點。教學片段2中在拋出核心問題之后，又用一連串問題（雖然他們數的位置都不同，但他們找的地方有什么相同之處嗎？你們還能在平移圖上找到其他對應點和對應邊嗎？想想它們之間的距離是幾格，你有什么發現？他們的數法為什么是錯的呢？現在你知道怎樣判斷格子圖上一個圖形平移的距離了嗎？觀察平移前后的圖形，你有什么發現？）把學生的思考聚焦到對“對應點或對應邊”的觀察、比較、辨析、概括、抽象上，把對“對應點或對應邊”的認識從直觀感知上升到獲得規律的層面，并能聯系到平移的本質上,從而使學生對平移的認識不斷深入，對平移的體驗越發深刻。

要想設計出好的數學問題，引領學生的深度學習，教師需要深刻理解所教學知識內容的數學本質。如果學科本質沒有把握好，問題設計就會偏離教學主題；好問題的設計還要準確了解學生的真實起點在哪里，只有準確把握學生學習的困惑，才能真正激發教師為學生解惑的動力；好的問題還應“少而精”，只有“少而精”，才能讓學生有較長時間思考，從而真正實現對問題的深度探究。