融合知識圖譜和協同過濾的學生成績預測方法

陳 曦，梅 廣，張金金，許維勝，3*

（1.同濟大學電子與信息工程學院，上海201804；2.同濟大學教育技術與計算中心，上海200092；3.同濟大學信息化辦公室，上海200092）

0 引言

學生成績預測是教育數據挖掘（Educational Data Mining，EDM）領域的研究熱點之一。研究通過對課程設置、學生歷史成績或其他背景數據的分析，預測學生在未來學習階段的表現。高等教育中日益嚴重的退學問題使采用更為創新有效的方法促進學生及時畢業已成為迫切需求：文獻［1］分析了全美的教育數據，發現在所有2011 年秋季入學攻讀四年制學士學位的學生中，僅有60%在6 年內完成了學業。眾多教育家認為早期成績預測是解決該困境的一種實用的方法：文獻［2-4］都曾通過一系列實驗表明早期識別出有退學風險的學生是防止他們輟學的一個關鍵舉措。

隨著數據挖掘技術在教育領域的興起，大量數據挖掘的方法被應用于學生成績預測的研究中。現有的研究方法可分為兩類：一類是將預測問題視為回歸或分類問題，應用線性回歸［5］、決策樹［6-7］、支持向量機［8］、深度神經網絡［9］、貝葉斯網絡［10］等數據挖掘模型。另一類是將學生預測問題類比成推薦系統中的用戶評價問題，借用推薦領域的技術解決問題，包括協同過濾（Collaborative Filtering，CF）、矩陣分解（Matrix Factorization，MF）等方法［11-17］。與基于回歸的方法相比，基于推薦的方法因為其較高的預測精度和可解釋性得到更為廣泛的應用。

但是，基于推薦的方法往往在缺乏歷史數據的情況下性能較差。該類方法主要依賴學生成績的歷史記錄挖掘課程的相似性，進而對結果進行預測，因此在課程的歷史選課人數較少時，必須采用額外的信息幫助準確刻畫課程之間的相似度。例如學生的知識基礎和課程的知識領域，這兩者之間的重合度與課程成績息息相關，如果能夠揭示出這種關聯，并運用到成績預測中，預測的精度將有機會得到改善。但在學生成績預測領域，大多數研究都只利用了與知識信息關聯較弱的學生背景信息或課程背景信息，包括學生年級、課程難度、課程學時等。這些背景信息通常類別冗雜，對數據源的要求較高，且對知識信息的挖掘有限。目前為止，還未見依賴知識信息預測學生成績的研究。

本文研究如何利用課程知識信息對高等教育中本科生在本科學位課程上所取得的成績進行預測。研究通過TextRank算法［18］從課程信息中提取關鍵字作為知識點，再結合數據庫中其他課程信息，構建了基于課程信息的知識圖譜Knowledge Graph，KG)來表示課程的知識信息。在知識圖譜的 幫 助 下，本 文 借 助 節 點 親 密 度 算 法（Adamic Adar［19］，Preferential attachment［20］，Resource Allocation［21］）和知識圖譜表示學習算法（Translating Embeddings［22］和DistMult Model［23］）挖掘課程之間的知識相關性，并比較了它們在傳統CF框架下的有效性。

本文的主要工作如下：

1）基于同濟大學2013—2017 年間的本科生課程信息構建了課程知識圖譜。

2）提出了一種在CF 框架下利用課程知識信息進行成績預測的方法，并利用同濟大學的本科生成績數據驗證了方法的有效性。

1 研究現狀

現有研究表明了基于推薦的算法在成績預測領域的有效性和利用課程信息建立教育類知識圖譜的可行性，為從知識層面發掘課程關系并應用于預測學生成績提供了理論基礎。

1.1 基于推薦算法的成績預測方法

學生成績預測問題常與推薦系統中的用戶評價問題進行類比，現有的研究也將推薦領域中的相關技術用于預測學生的成績。文獻［11-12］使用CF 方法預測成績并證明了CF 在學生成績預測上的表現優于傳統回歸方法。文獻［13］以CF為底層算法構建了一個選修課推薦系統并應用在中山大學。該應用使得選修課程的退課率大幅下降，進一步證明了CF的有效性。文獻［14］擴展了傳統的推薦算法，利用學生的歷史成績以及喬治梅森大學的各種課程背景資料和學生資料解決成績預測問題；研究提出了一種混合分解機和隨機森林（Factorization Machine with Random Forest，FM-RF）的方法用于準確預測學生在課堂上的表現。文獻［15］在CF 框架下開發了三種融合了時間信息的預測方法，并對明尼蘇達大學的學生成績數據進行了一系列實驗，驗證了方法的有效性。

上述成績預測方法大多忽略了學生成績隨著學生努力程度而改變的事實基礎。為解決上述問題，一些研究者基于學生的學習過程對成績的影響提出了動態預測算法：文獻［16］使用歷史成績信息和可用的附加信息（如期中考試成績）來預測學生未來課程的成績，研究采用MF 方法并得到了較好的結果；文獻［17］在評估學生行為的基礎上，提出了一種基于MF的動態預測學生學習成績的方法。

1.2 教育知識圖譜的構建和應用

在教育領域，知識圖譜也稱概念圖［24］或領域模型［25］，主要關注包括課程和知識在內的教育實體及其之間的連接關系。挖掘每門課程的關鍵知識是構建課程知識圖譜的過程中必不可少的一步。挖掘關鍵知識的一類方法是使用關鍵字提取 算 法，包 括TextRank［18］和TF-IDF（Term Frequency-Inverse Document Frequency）［26］。該類方法將課程信息視為普通文獻，提取其中的關鍵字作為關鍵知識，文獻［27］就使用關鍵字提取方法基于MOOC課程信息構建了課程知識圖譜。另一種方法是利用實體鏈接技術識別知識點。例如：文獻［28］利用教學數據和實體識別技術，從MOOC 平臺的課程信息中提取了教學概念；文獻［29］提出了一種利用Web 知識從數字圖書中提取概念層次結構的方法，并通過該方法將圖書內部的知識與外部的知識資源連接起來；文獻［25］提出了一種從電子教材中半自動生成知識模塊的框架DOM-Sortze。

知識圖譜特殊的結構為計算節點的相似度提供了可能性。將知識圖譜看作由節點和邊組成的網絡結構，可以使用一些鏈路預測方法來計算節點間的緊密度，包括Adamic Adar［19］、Preferential attachment［20］以及Resource Allocation［21］。一些知識圖譜表示學習算法也可以用于計算每個節點的特征向量，從而計算節點相似度，如TransE（Translating Embeddings）［22］、DistMult［23］和ComplEx［30］。

2 課程知識圖譜的構建

本章設計了課程知識圖譜的結構，并使用TextRank［18］對知識圖譜進行實體提取，以完成圖譜的構建。

2.1 知識圖譜結構

本文研究使用同濟大學的課程信息相關數據構建課程知識圖譜。通過對數據的分析，本文選取了以下實體：“院系”“課程”“知識點”“教材”“參考書”和“教學模式”。“院系”實體指開設該課程的機構；“知識點”實體指學生在完成課程后應該掌握的概念或技能；“教學模式”實體指教學過程中所采用的教學方法，如講課、討論或實踐。圖1 描述了幾個實體之間的關系類型：圖中節點代表實體，邊緣代表實體之間的關系。圖2 展示了部分知識圖譜；圖譜以“模式識別”“模式信息處理”及“模式識別及其地學應用”這三門課程為中心發散，展現了三門課程之間的聯系。其中圓形節點表示“課程”實體；白色矩形節點表示“知識點”實體；灰色矩形節點表示“院系”實體；實線箭頭表示“院系-OFFER-課程”關系；虛線箭頭表示“課程-COVER-知識點”關系。可以看出，知識圖譜可以直觀地反映課程的相關特征以及不同課程之間的聯系。

2.2 課程知識相關性挖掘

課程知識圖譜中涉及的大部分實體和關系可以從數據庫中獲取。而“知識點”實體需要從課程簡介中提取。課程簡介的文本往往結構統一，大都包含相似的詞匯和句型。除去通用詞匯，課程簡介主要由專業術語組成。綜上，利用簡單的關鍵字提取方法即可提課程簡介中所包含的關鍵知識點。本節使用TextRank從中提取“知識點”。

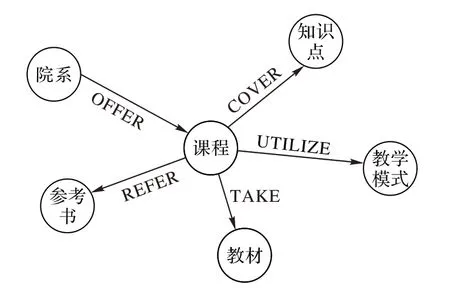
圖1 課程知識圖譜的結構Fig.1 Structure of course knowledge graph

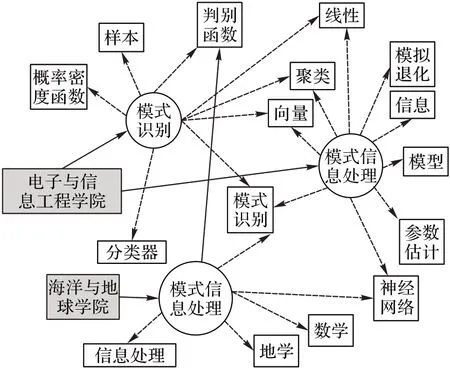
圖2 知識圖譜示例Fig.2 Sample of knowledge graph

TextRank 的主要思想是建立基于詞之間鄰接網絡，并使用PageRank［31］計算每個節點的Rank。算法選擇Rank 數值較大的單詞作為關鍵詞。首先將給定的課程簡介文檔D分成完整的句子[S1，S2，…，Si]；對句子Si進行分詞和詞性標注。分割后從句子中過濾停止詞，留下帶有指定詞性的單詞。停止詞包含一些常見但無意義的詞，如“學時”“課堂”“理論”和“大學”。根據上述規則將Si分成一組單詞[ti，1，ti，2，…，ti，n]，其中，ti，n表示句子中的第n 個候選單詞。算法根據這些單詞構建候選關鍵字網絡G=(V，E)，每個候選單詞ti，n對應一個節點，V 是所有節點的集合；E 則是由代表節點之間共現關系的邊組成的集合。共現關系是指一對節點對應的兩個詞在長度為K 的文本窗口內共現。在本文中，K 設置為30。根據式（1）迭代計算各節點的Rank(Vi)直到收斂，再選擇Rank(Vi)的數值較大者作為關鍵詞。

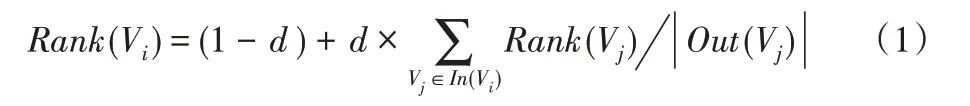
其中：d 為用于平滑的參數；In(Vi)是Vi的前繼節點，Out(Vj)為Vj的后繼節點。

TextRank 雖然可以有效地從課程簡介中提取關鍵字，但無法識別知識點間的歧義現象。例如，“神經網絡”一詞在“模式識別”和“人體解剖學”兩門課程中就有不同的含義。由于該詞匯在這兩篇文檔中具有相同的詞性和所處語境的相似性，很難將其區分開來。

一個術語的意義取決于它的領域；在本文中，這體現在課程所處“院系”和課程包含的“知識點”這兩個實體上；即“模式識別”課程由“電子與信息工程學院”開設，“人體解剖學”課程由“醫學院”開設，且這兩門課程涵蓋的“知識點”存在顯著差異。對含有相同關鍵詞的課程，比較其所屬院系和包含的“知識點”。如果這兩門課程來自不同的院系或超過一半的“知識點”是不同的，即認為兩門課程不屬于同一知識領域，可能在同一個關鍵詞上有不同的含義。考慮到數據庫中存在大量的交叉學科課程，本文在上述歧義檢測的基礎上進行人工確認，從而確保消歧過程的準確性。

3 成績預測方法

基于已構建的課程知識圖譜，分別采用基于鄰節點的方法和基于知識圖譜表示學習的方法從知識圖譜中挖掘課程相似度，該相似度揭露了課程在知識領域的關系。在缺乏歷史數據的場景下，課程在知識層面的關聯為CF框架提供了相似度的計算途徑；知識相似度與基于歷史紀錄的相似度之間互為補充，使得預測結果更接近真實數據。

3.1 算法框架

算法首先生成課程相似度矩陣，再選取k 個與目標課程相似度最大的課程作為相似課程。學生在相似課程上分數的加權平均值即為學生在目標課程獲得的分數。當預測學生s在課程c 上所取得的成績時，根據課程知識圖譜計算c 和s 上過的歷史課程[c1，c2，…，ci]的知識相似度。基于知識相似度篩選出相似度高的k個課程。s在這k門課程上所得成績的加權平均即為目標課程c的成績估計est1，計算加權平均值時以知識相似度為權重。本文也使用基于歷史記錄的傳統CF 生成估計值est2。對這兩種預測模型作線性集成，得到最終預測ScoreEst。圖3給出了算法流程。

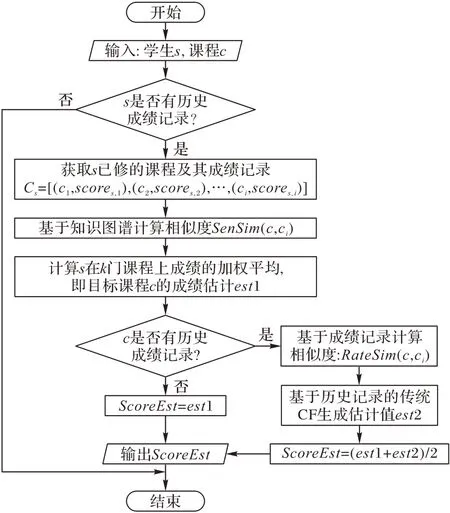
圖3 預測算法流程Fig.3 Flowchart of prediction algorithm

3.2 相似度計算

3.2.1 基于鄰節點的相似度計算

基于鄰節點的相似度計算方法將知識圖譜看作由節點和邊構成的網絡，用課程對應節點之間的親密度衡量課程相似度。本節采用了多種基于鄰節點的節點親密度算法來計算課程間的知識相似度，并按照3.1節所述與CF框架融合。

在基于鄰節點的方法中，鄰節點的數量對于確定一對節點的相似性起著至關重要的作用。兩個節點共享的鄰節點越多，關系就越親密。本文使用了一些經過鏈路預測領域驗證的節點親密度計算方法，包括Adamic Adar［19］、共享鄰節點數量（Common Neighbors）、Preferential Attachment［20］、Resource Allocation［21］、同屬社區（Same Community）和鄰節點總數量（Total Neighbors）。具體的計算公式如（2）～（6）所示。

對于Adamic Adar：

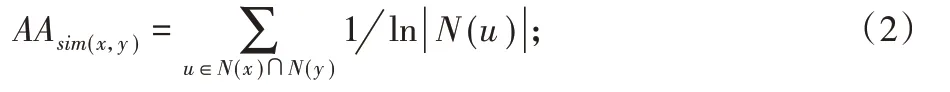
其中：N(u)表示u的鄰節點，| |

N(u)表示N(u)的節點數量。

對于Common Neighbors：

對于Preferential Attachment：

對于Resource Allocation：

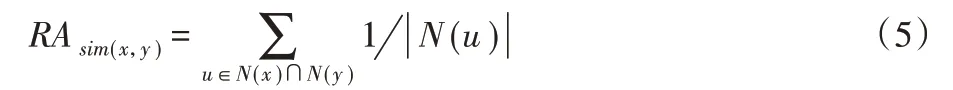
Same Community是通過確定兩個節點是否屬于同一社區來決定兩節點關系的一種方法。該算法將網絡劃分為不同的社區，值為0 表示兩個節點不在同一個社區中，值為1 表示同屬一個社區。本文定義課程知識圖譜中同一個連通域內的點屬于同一個社區。

利用上述公式計算課程所對應節點的親密度，并將其作為課程之間的相似度應用于后續計算中。

3.2.2 基于圖譜表示學習的相似度計算

知識圖譜的表示學習是一種將知識圖譜的實體和關系轉化為低維向量的方法。為了將實體和關系嵌入到低維向量空間中，使用三元組的集合表示知識圖譜。以本文為例，課程知識圖譜G 可以看作三元組(sub，pred，obj)的集合，每個三元組包含一個主體sub ∈Entity，一個謂詞pred ∈Relation，以及一個對象obj ∈Entity。Entity 和Relation 分別是所有實體和關系類型的集合。例如，“課程”實體C 以及“院系”實體D 連接形成一個三元組：(D，offer，C)。推斷三元組中的一對節點在知識圖譜的語義上是相似的。有效的知識圖譜表示形式應該能夠將圖譜中存在的三元組（正三元組）和不存在的三元組（負三元組）區分開，即正三元組中，實體所對應的嵌入向量相似，負三元組中，實體所對應的嵌入向量差異大。本文采用了TransE［22］和DistMult［23］對圖譜進行低維嵌入。得到嵌入向量之后，使用Pearson 距離來度量向量之間的相似度，從而得到課程之間的相似矩陣。

TransE 和Distmult 使用評分函數S(t)對正三元組t+和負三元組t-評分；再通過合適的損失函數盡可能地讓負三元組的得分顯著低于正三元組。

本文中，TransE的評分函數采用L2范數：

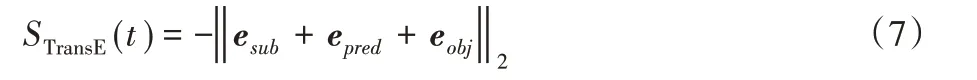
對于Total Neighbors：

其中，esub、epred、eobj分別表示sub、pred、obj的嵌入向量。

DistMult模型采用三線性點積作為評分函數：

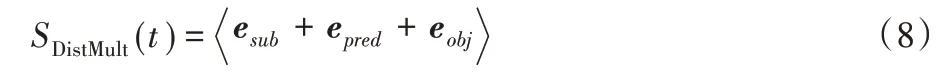
本文中采用了pairwise 損失函數和negative log-likelihood損失函數訓練TransE和DistMult，計算公式如（9）和（10）。

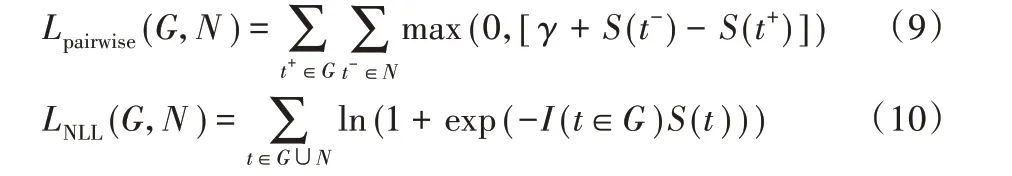
其中：γ為邊緣參數，表示正負三元組的區分度；G是正三元組的集合，N 是負三元組的集合，由替換正三元組的sub 或obj而生成；I()是指示函數，I(t ∈G)在t ∈G的時候取1，其余為0。

使用上述方法計算得到的k 維向量表示課程，并生成相似度矩陣。

相對于基于鄰節點的方法，基于知識圖譜表示學習的方法考慮了不同關系具有的不同意義。例如，來自同一“院系”的課程比只有一個共同“知識點”的課程在知識層面上更相似。但在以鄰節點為核心的方法中，相似度只與共同鄰節點的數量相關。

4 實驗與討論

為驗證學生知識基礎和課程知識信息在學生成績預測中的有效性，本文進行了一系列對比實驗來衡量提出的預測算法在不同場景下的預測精度，實驗場景包括冷啟動問題、數據稀疏場景和數據密集場景。

4.1 實驗設置

4.1.1 數據集

實驗中采用的數據集是來自同濟大學的1 217 086 條課程成績記錄。數據集涉及23 903名本科生和5 378門課程，涵蓋了2013 年至2017 年所有在校本科生的課程記錄。每一項成績記錄描述了學生、課程以及相應的課程成績（5 分制）。圖4描繪了課程數量關于選課人數的分布；圖5則是學生數量關于選課數量的分布情況。

如圖4 所示，大部分的課程選課人數在［10，500）區間。僅有11.64%的課程選課人數少于10人，即11.64%的課程會出現數據稀疏或冷啟動問題。使用傳統CF 對這部分課程進行成績預測的效果有限。

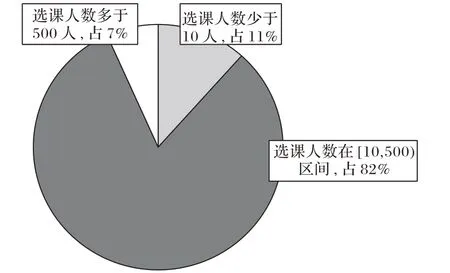
圖4 課程數量關于選課人數的分布Fig.4 Distribution of number of courses corresponding to number of students

從圖5的數據可以得出，95.14%的學生的選課數量在10到100 之間，數據表明大部分學生擁有足夠的成績記錄來保證預測的準確性。只有0.41%的學生選課門數少于10門，這些學生多是交流生或聯合培養項目參與者，他們的成績計算方法及成績記錄仍保留在原學校，因此不屬于本文研究的探究范疇。

在實驗過程中，按照3∶1 的比例將數據集劃分為已知成績數據集和測試數據集。實驗將記錄每一種算法在已知部分成績數據的基礎上預測成績的誤差。

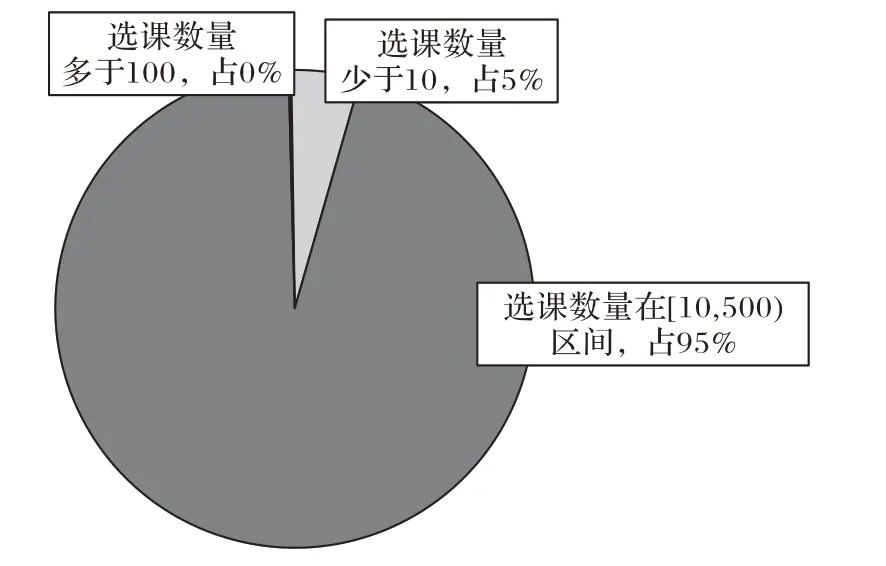
圖5 學生人數關于選課門數的分布Fig.4 Distribution of number of students correspongding to number of taken courses

4.1.2 課程知識圖譜

本文構建的課程知識圖譜組成如表1、2所示。

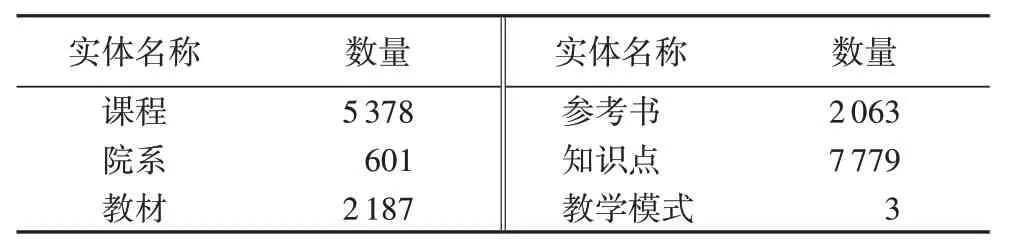
表1 實體類型及其數量Tab.1 Types and numbers of entities

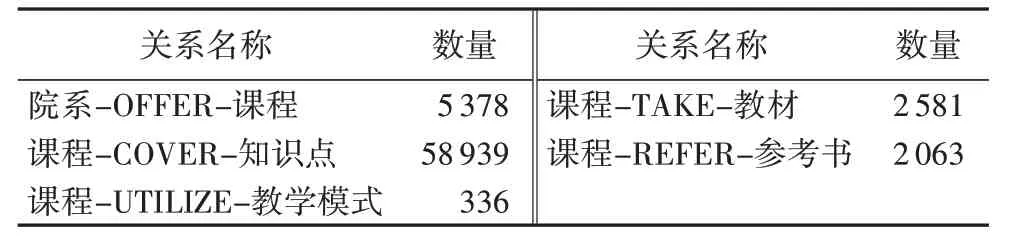
表2 關系類型及其數量Tab.2 Types and numbers of relationships

課程知識圖譜共有69 297個三元組，選取其中的2 000個作為訓練嵌入向量模型的測試集，并通過嵌入向量模型在測試集上的表現評價生成的嵌入向量。

4.1.3 評價指標

實驗采用均方根誤差（Root Mean Square Error，RMSE）和平均絕對誤差（Mean Absolute Error，MAE）兩個指標對預測結果進行了評估，計算公式如式（11）、（12）。

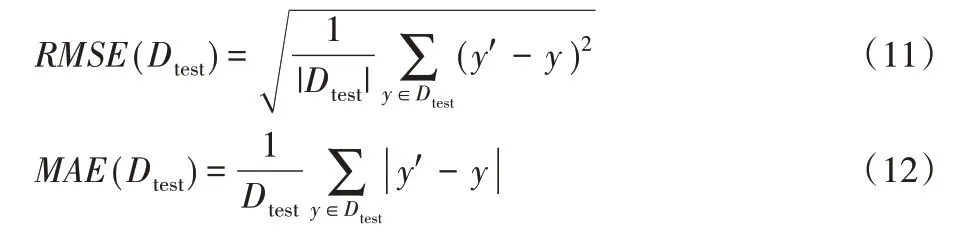
其中：Dtest表示測試集；y'和y 分別表示樣本的預測結果和該樣本的實際得分。

本文使用平均互反排名（Mean Reciprocal Rank，MRR）和Hit@10 評價嵌入向量的準確性。對于測試集中的每個正三元組，實驗通過替換它的主體或對象來生成一系列的負三元組。模型使用得分函數計算這些正負三元組的得分并按得分降序排列三元組；其中正三元組在其生成的一系列負三元組中排名為rank(s+，p，o+)。Hit@10是指排在前10位的正三元組的比例。MRR則按照式（13）計算。

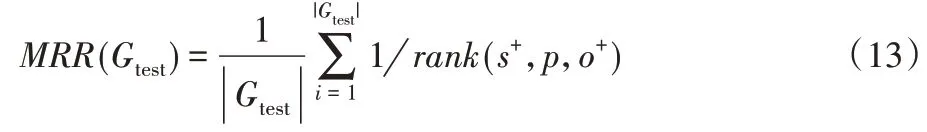
其中Gtest表示測試三元組的集合。

MRR和Hit@10的數值越大，說明測試集中排名靠前的正三元組數量越多，即嵌入向量對知識圖譜的描述能力越強。

4.1.4 基準

實驗采用三種常用成績預測算法在數據集上的實驗結果作為基準。一是基于正態分布的成績預測方法（Normal Prediction），該方法將所有學生在某一門課程上獲得的成績視為正態分布，通過隨機取樣獲得待預測成績；二是基于奇異值分解（Singular Value Decomposition，SVD）的矩陣分解方法［32］。三是基于項目的協同過濾（Item-Based CF）方法，該方法采用Pearson距離來衡量課程之間的相似性，并選取學生在40個相似課程上的成績加權平均值作為預測值。實驗通過對比每種預測方法得出的實驗結果與三種基準算法中的最優結果，檢驗知識圖譜對預測算法的優化程度。

4.2 基于鄰節點的方法

實驗融合了傳統CF和基于鄰節點的相似度，并從整個數據集中選取了3 段具有代表性的數據來檢驗鄰節點法的有效性：1）選課人數少于10 人的課程；2）選課人數在［10，500）區間的課程；3）選課人數大于500人的課程。場景1的課程選課人數較少，冷啟動問題和數據稀疏問題較嚴重；場景2 幾乎不存在冷啟動問題，數據稀疏問題有所減輕；場景3 為數據密集場景。表3記錄了算法在數據稀疏性不同的場景下的性能。

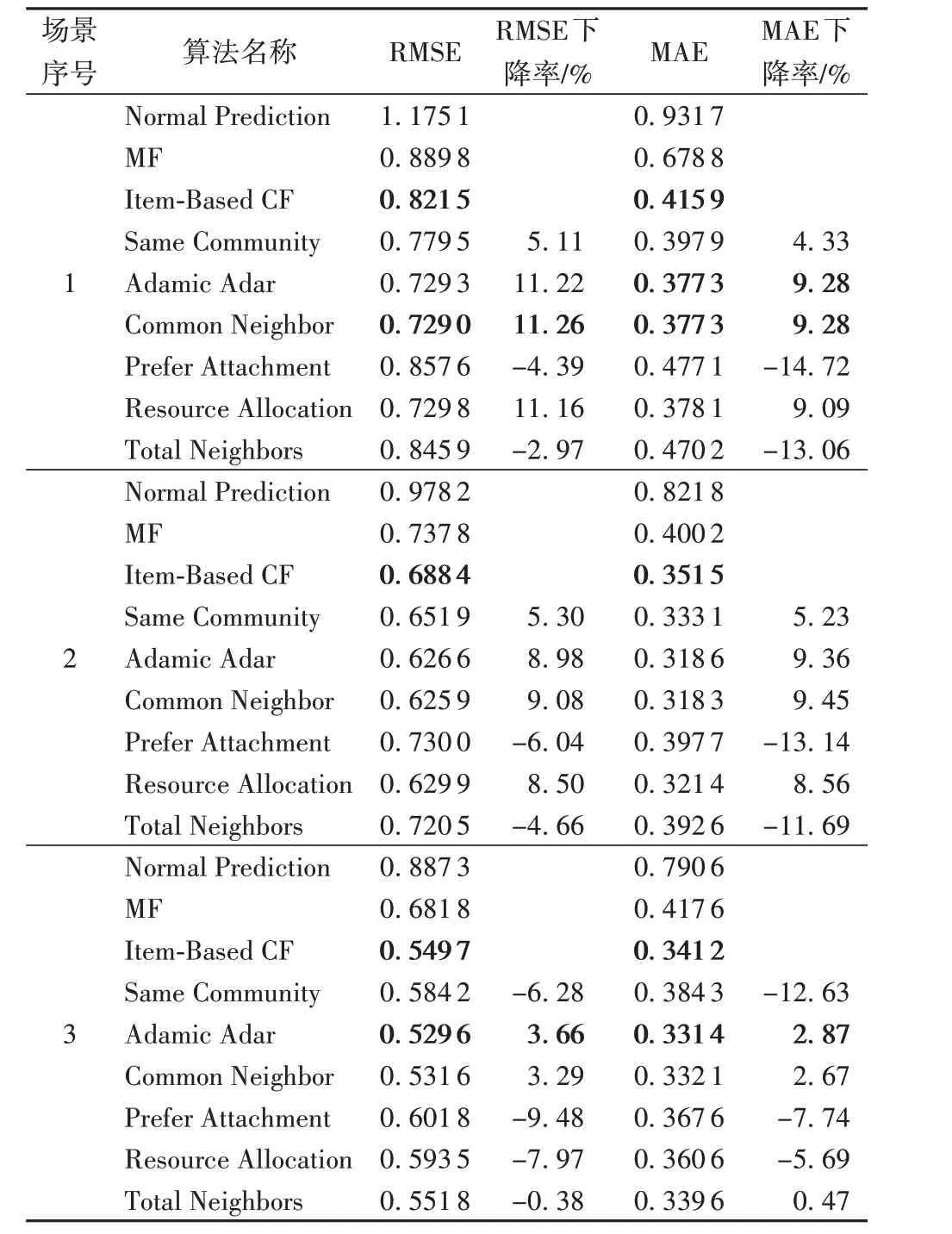
表3 基于鄰節點的算法多場景下的性能Tab.3 Performance of neighbor-based algorithms in multiple scenarios

從實驗結果可得，在冷啟動和數據稀疏的場景下，基于鄰節點的方法顯著降低了預測誤差。表3中場景1數據顯示，在數 據 稀 疏 場 景 下，Resource Allocation、Adamic Adar 和Common Neighbor 與結果最優的基準算法相比都在RMSE 指標上下降了超過10%，在MAE 指標上下降約9%。此外，場景2和場景3的數據表明，知識圖譜在選課人數較多的情況下仍對預測結果有改善。對于選課人數在［10，500）區間的課程，與Item-based CF 方法相比，基于鄰節點的方法使RMSE 和MAE 分別下降了9%；對于選課人數大于500 人的課程，性能最優的算法Adamic Adar 與Item-Based CF 方法相比，其RMSE下降了3.66%，MAE 下降了2.87%。綜合表3 的數據，可以發現傳統CF的性能隨著歷史數據的豐富而逐漸變好，而知識圖譜的作用隨著數據稀疏程度的減弱而減弱。

4.3 基于圖譜表示學習的方法

本節在傳統CF 中融合通過TransE 和DistMult 計算的相似度。實驗首先利用課程知識圖譜生成嵌入向量，并用MRR和Hit@10對嵌入向量進行評價。經過訓練和驗證，設置嵌入向量的維度為200；本文使用Pairwise 損失函數訓練TransE，使用negative log-likelihood 損失函數訓練DistMult。表4 給出了兩種嵌入向量的詳細評價。

表4 TransE和DistMult的評價Tab.4 Evaluation of TransE and DistMult

利用Pearson 距離計算嵌入向量的相似性。為了驗證基于知識圖譜表示學習的方法的有效性，從整個數據集中選取與4.2節同樣的三段數據進行實驗，結果如表5所示。

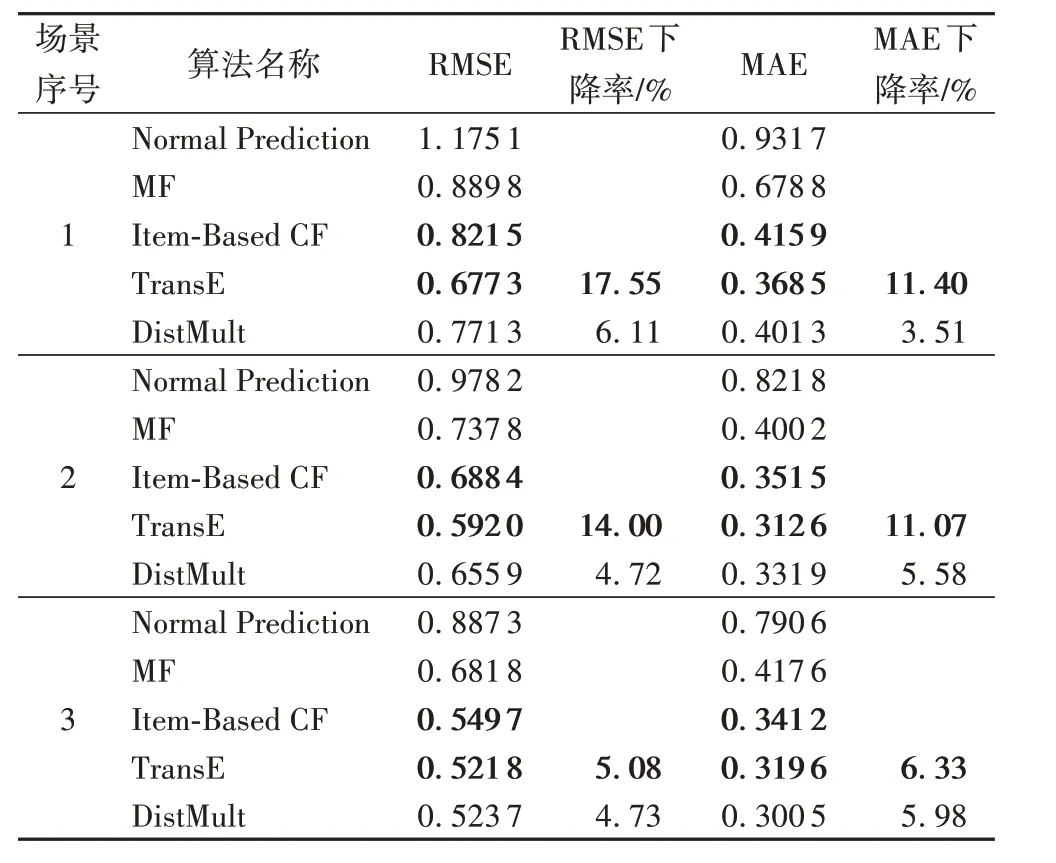
表5 基于圖譜表示學習的算法在多場景下的性能Tab.5 Performance of KG representation-based algorithms in multiple scenarios

表5 說明了基于圖譜表示學習的方法對傳統CF 的預測結果有顯著的改善。場景1）數據顯示在數據稀疏場景中，性能最優的算法與Item-Based CF 相比在RMSE 和MAE 指標上分別下降了17.55%和11.40%。隨著數據的豐富，基于圖譜表示學習的方法相比于傳統CF依然有優勢，且在各個場景下的預測性能都優于基于鄰節點的方法。比較TransE 和DistMult，盡管DistMult 在描述知識圖譜（包括MRR 和Hit@10）方面的性能優于TransE，但TransE在上述幾種情況下的表現都優于DistMult。

4.4 結果分析

本文研究結果表明，知識圖譜可以幫助傳統CF實現更準確的學生成績預測。在冷啟動和稀疏數據的情況下，基于鄰節點的方法和基于圖譜表示學習的方法均使RMSE 和MAE顯著下降。實驗結果顯示，使用Adamic Adar、Common Neighbors、Resource Allocation、Same Community、Total Neighbors、TransE 和DistMult 等算法計算的知識相似性有助于預測結果的改善。這種改善可以歸因于知識圖譜提供的語義信息。傳統CF往往通過歷史數據評估相似度，不同課程之間對學生能力要求的共性和學科之間思維模式的相通性確保了傳統CF能夠有效地刻畫課程間的聯系，從而取得不錯的預測效果。但在歷史記錄缺乏的場景下，小數據量不足以支持CF 準確地刻畫課程間的關系。而利用課程知識信息構建的知識圖譜可以作為相似度計算的另一種途徑；知識圖譜更偏重于從教學內容挖掘課程之間的關系，它刻畫了不同課程在知識領域上的交集；從學生的先驗知識和課程的教學內容出發，提供預測結果。

實驗結果還表明，隨著數據稀疏程度的減弱，知識圖譜對預測精度的改善逐漸減弱。對此可能的解釋是信息的冗余。以往的文獻都證明了CF 在歷史評分數據充足的場景下可以有效發掘課程之間的關聯，這種關聯既包括學科之間邏輯思維層面的相通性，又涵蓋了知識層面的共同性。在歷史數據不足的情況下，知識圖譜提供的信息揭露了課程在知識層面的交叉，從而有助于表示課程關系，幫助CF 框架更好地預測成績。在密集數據情況下，知識圖譜所包含的信息和歷史數據本身發生冗余；因此，在歷史數據密集的場景下，知識圖譜對預測性能的提升有限。

5 結語

本文研究通過結合關鍵字提取算法和消歧方法構建了一個課程知識圖譜模型；并從圖譜結構和語義信息兩個角度出發，分別使用基于鄰節點的方法和基于圖譜表示學習的方法發掘了課程在知識層面的關系；本文隨后對其在學生成績預測中的應用進行了探討。實驗結果表明，知識圖譜可以從知識領域的層面有效計算課程相關度；對傳統CF在歷史記錄基礎上得出的課程關聯作了信息補充，對課程關聯作了更加完善的刻畫，從而得到了比傳統CF更好的預測性能。

本文探索了知識圖譜在學生成績預測中的應用，并驗證了其可行性和有效性。與傳統的成績預測研究相比，本文提出的方法融合了學生的知識基礎和課程的教學內容，為后續解讀預測結果提供了更多角度。

然而在本文研究中，知識圖譜的結構不夠細化，限制了語義信息進一步的挖掘。例如，本文提出的“知識點”實體可以分為幾個子類型，如技能、概念、公式和理論。更詳細的知識圖譜將會暴露更多的語義信息。后續將對知識圖譜的結構作進一步的優化。此外，本文研究只是將知識圖譜與CF框架進行了簡單的整合，未來的研究可以考慮將知識圖譜應用于更多的推薦算法框架，進一步優化預測性能。