探析二次函數圖形中的面積問題

丁小將

【摘 要】函數是初中數學的重要知識點，二次函數在初中數學中的地位舉足輕重。在過去的近二十年中，二次函數圖形中的面積問題一直是各類考試命題的重要知識點，每年無論在中考模擬考試還是在中考考試中，幾乎都是必考題。筆者根據多年的教學經驗和體會，適當總結和歸納了這類問題。以期為初中教師提供借鑒，提高學生的探究、分析、解決問題的能力。

【關鍵詞】二次函數;面積;數形結合;函數模型

【中圖分類號】G633.6? 【文獻標識碼】A? 【文章編號】1671-8437（2020）28-0053-02

二次函數是初中數學教學的核心內容，以二次函數為背景的數學問題有多種類型，其中面積問題非常典型。二次函數圖形中的面積問題看似研究面積問題，實際上在解決圖形面積問題的過程中，需要學生掌握很多相關的基本知識，如基本圖形的面積公式、相關函數解析式的求法、點的坐標、線段的長度、相關函數的性質。有時對于一些不規則圖形面積的計算，需要采取割、補的方法，充分利用數學中的轉化思想，把不規則的圖形轉化成可以利用面積公式進行計算的規則圖形[1]。筆者以一道二次函數為背景的綜合題為例，從以下幾個方面討論常見的二次函數為條件的面積問題。

1? ?原題呈現，主要考點分析

已知拋物線的頂點為（1，-4），并經過點（4 ，5），

（1）求拋物線的解析式;

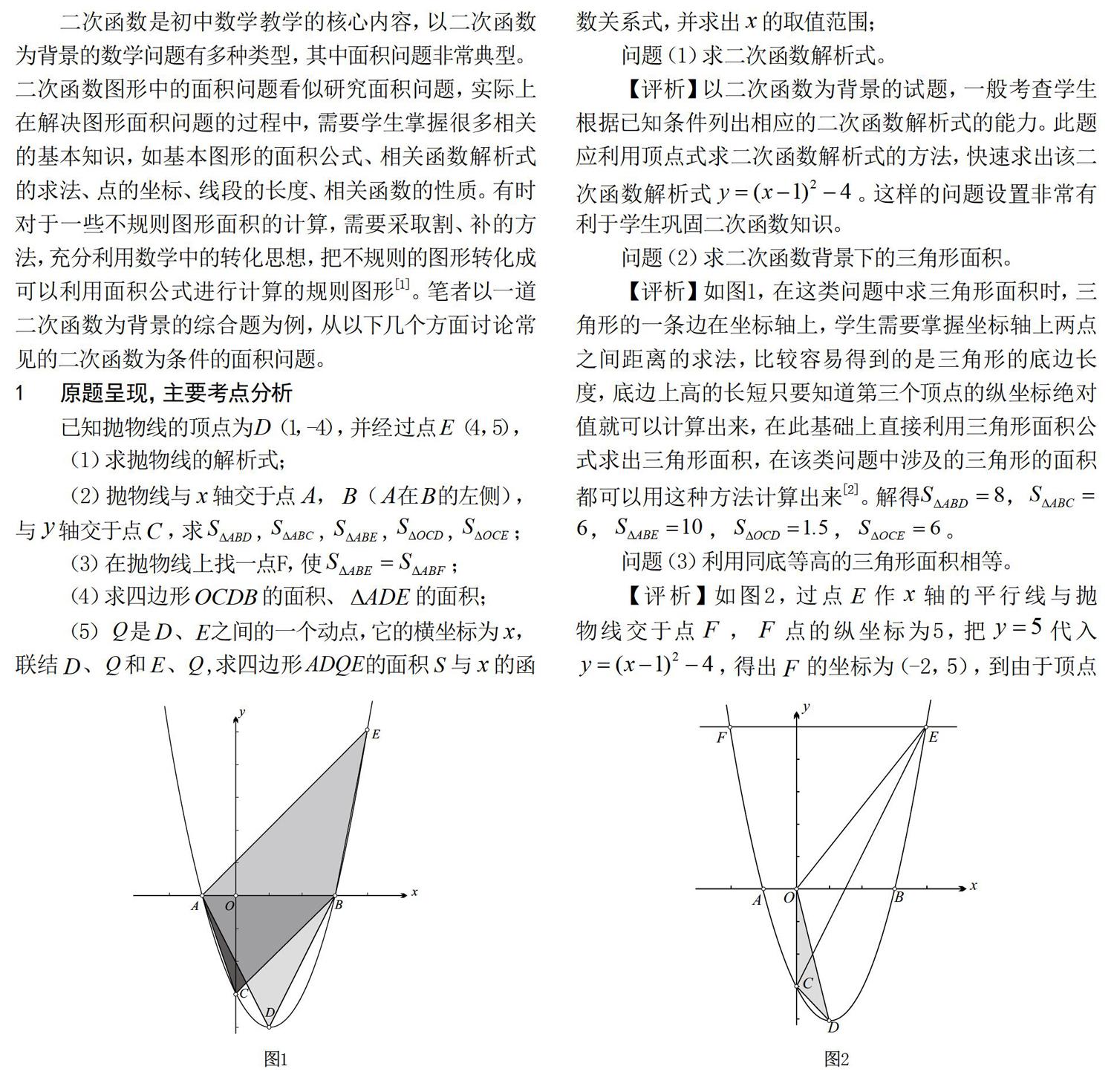
（2）拋物線與軸交于點，（在的左側），與軸交于點，求，，，，;

（3）在拋物線上找一點F，使;

（4）求四邊形的面積、的面積;

（5）是、之間的一個動點，它的橫坐標為，聯結、和、，求四邊形的面積與的函數關系式，并求出的取值范圍;

問題（1）求二次函數解析式。

【評析】以二次函數為背景的試題，一般考查學生根據已知條件列出相應的二次函數解析式的能力。此題應利用頂點式求二次函數解析式的方法，快速求出該二次函數解析式。這樣的問題設置非常有利于學生鞏固二次函數知識。

問題（2）求二次函數背景下的三角形面積。

【評析】如圖1，在這類問題中求三角形面積時，三角形的一條邊在坐標軸上，學生需要掌握坐標軸上兩點之間距離的求法，比較容易得到的是三角形的底邊長度，底邊上高的長短只要知道第三個頂點的縱坐標絕對值就可以計算出來，在此基礎上直接利用三角形面積公式求出三角形面積，在該類問題中涉及的三角形的面積都可以用這種方法計算出來[2]。解得，，，，。

問題（3）利用同底等高的三角形面積相等。

【評析】如圖2，過點作軸的平行線與拋物線交于點，點的縱坐標為5，把代入，得出的坐標為（-2，5），到由于頂點（1，-4）到軸距離為4，所以在軸下方沒有符合條件的點。同底等高的三角形面積問題中，三角形的頂點到底邊的距離均相等，利用這一特點，結合二次函數圖象的對稱性，各個三角形第三個點的縱坐標相同或者互為相反數，把縱坐標代入函數解析式即可得出所求點的坐標。

問題（4）在二次函數條件下的不規則四邊形、底邊不在坐標軸上的三角形面積的求法。

【評析】這類問題的解題思路是利用圖形的“割”或者“補”的方法，把不規則的四邊形分割成可以利用面積公式計算的四邊形和一條邊在坐標軸上三角形進行面積的計算，充分利用數學中的轉化思想使問題迎刃而解。圖3中，，，，，

四邊形的面積。

關于圖中的面積的計算，由于該三角形沒有邊在坐標軸上，所以它的面積也不能直接利用三角形面積公式，問題可以用“割”的方法來解決，，需要先求出DE所在的直線函數解析式，點，則。問題（5）在二次函數條件下，根據不規則四邊形面積構造函數關系式。

【評析】如圖4，解決這個問題需利用面積構造函數關系式。圖中的四邊形不是規則的四邊形，想直接利用面積公式解決問題顯然行不通，所以需要利用面積分割的方法，通過添加輔助線把這個四邊形面積分割成，其中，在問題（4）的求解中已經得到答案，四邊形ADQE的面積=，仍然要再一次分割，其中線段長度需要借助點、點的縱坐標計算，同時還需要借助二次函數和一次函數表示、的坐標。這道題對學生分析問題能力的要求較高，在正確表示面積方面難度也較大。

2? ?二次函數背景下面積問題的思考

通過分析常見的二次函數背景下的面積問題，讓學生在中考二模后的復習中更加系統地掌握這類問題，并加以鞏固，使其熟練地掌握二次函數、一次函數解析式的求法和兩點間距離公式。通過三個例題的分析，從一條邊在坐標軸上的三角形面積的求法到二次函數圖像上的點構成的三角形、四邊形面積的求法，在這類問題中利用“割”或“補”的方法，把這些圖形的面積求法轉化成邊在坐標軸上一類的面積處理。求面積問題中常見的模式有同底等高、同底不等高一類面積問題的處理要想到對應的處理的方法，如幾個三角形同底，而第三點所在的直線平行于同底的邊，這類問題的出現讓學生產生作平行線的意識。通過問題的層層鋪墊，提升學生能力，如例題中第五問以二次函數為背景的一道函數解析式的探究，有利于培養學生的分析問題的能力和綜合應用能力。

【參考文獻】

[1]胡玲君.2019年中考“函數”專題解題分析[J].中國數學教育（初中版），2020（1）.

[2]許力凡.借力題目創編引領學生探究[J].中國數學教育（初中版），2019（7）.