數形結合思想在數學教學中的滲透與應用

【摘 要】本文基于數形結合思想在激發學生興趣、促進數學知識理解和提高學生數學思維品質等方面的意義，提出數形結合思想在數學教學中應用的實踐與思考，通過以形助數，培養學生的數感;借助以數解形，幫助學生建構空間觀念;并在數形兼顧中發展學生的數學核心素養。

【關鍵詞】數形結合思想;數學;應用

【中圖分類號】G633.6? 【文獻標識碼】A? 【文章編號】1671-8437（2020）28-0133-02

數學家華羅庚說過這樣一句話：“數缺形時少直觀，形少數時難入微。”這句話既揭示出“數”和“形”各自的優勢，“形”具有“直觀”特點，“數”具有“入微”優勢;也揭示出數形結合思想是數學重要的思想。應用數形結合思想有利于提高數學教學的實效性，引領學生逐漸了解數學知識的本質[1]。

1? ?數形結合思想在數學教學中的滲透與應用價值

初中階段是數學思想形成的關鍵時期。數形結合思想對初中生數學素養的發展有較好促進作用，具體表現在以下幾個方面。

1.1? 激發學生的數學學習興趣

不少中學生感覺數學學習比較枯燥乏味，因此學習數學的熱情不高。在數學教學中，應用數形結合思想能優化數學教學方法，將抽象的問題直觀化，發揮中學生形象思維發達的優勢，引領學生從現象深入數學本質，將復雜問題簡單化，抽象問題直觀化，從而較好地激發學生的數學學習興趣，讓學生愛上數學。

1.2? 促進學生對數學知識的理解

初中數學相對小學數學，其難度有顯著的提升，各個知識點之間的關系錯綜復雜，在無形中加大了學生學習數學知識的難度，要求學生的數學認知結構更加系統化，數學思維更加開放、多元。在初中數學教學中，應用數形結合思想，借助數形互補的優勢，讓數學本質更好地表現出來，有利于促進學生對數學知識的理解。

1.3? 提高數學思維品質

初中生學習數學需要調動思維，一旦思維斷層，數學學習就難以繼續。“數”與“形”從本質上來說體現出了兩種思維模態，“數”體現的是抽象思維，“形”體現的是形象思維，數形結合思想則致力于實現抽象思維和形象思維的和諧，借助形象思維進入數學的抽象世界，同時又借助抽象思維，豐富學生的形象思維，最終達到提高學生數學思維品質的目的。

2? ?數形結合思想在數學教學中的滲透與應用實踐

數形結合思想是數學思想體系的重要組成部分，“數”與“形”是相輔相成的關系，主要包括三種基本形式，以形助數、以數解形和數形兼顧。

2.1? 以形助數，培養學生的數感

數學學科的一個重要任務是培養學生的數感。然而在初中數學教學中，數量關系往往具有抽象性，這就加大了學生數學學習的難度。教師可以應用數學結合思想，借助“形”助力“數”，引導學生通過直觀的圖形、符號等，解構數量關系，這樣就能夠使抽象的數量關系借助圖形變得直觀，以幫助初中生找到解決問題的方法，增強學生的數形結合意識，促進學生數感的形成。如在“絕對值”的教學中，如果采用傳統的講解法，不僅教師教得吃力，學生也難以完全理解。在教學中，不妨應用數形結合思想。在導入環節，教師可以利用多媒體動畫演示兩只貓，都從原點出發，沿著筆直的街一只向左、一只向右奔跑，都跑了5米，右邊達到A點，左邊達到B點。這時，要求學生畫出數軸，并引入問題：“A、B又體現出什么特征？”。最后，對情境反映的現象進行抽象：生活中，如果無視數的正負性質，需要引入絕對值概念。

這個環節，借助多媒體動畫演示創設情境，較好地激發了學生的學習興趣，使學生的注意力集中在課堂上。在此基礎上，教師可要求學生根據觀察到的畫面，自己動手以數軸的形式將動畫內容表現出來，促進數和形的有機結合;再從數軸進行抽象，借助直觀形象的情境利用及直觀的數軸，以“形”幫助學生認識“數”，使絕對值相關知識的引入水到渠成，也較好地培養了學生的數感。通過優化設計導入環節，也為學生學習絕對值做了較好的鋪墊。要達到以形助數的預期目標，教師需要針對“數”的內容，精心設計，充分思考“形”的符號語言，從而借助適合的“形”促進學生對“數”的認知。想要表現出數學知識之間的邏輯關系，教師不妨選擇思維導圖，讓學生借助思維導圖之“形”形成深刻的數學認知。

2.2? 以數解形，建構空間觀念

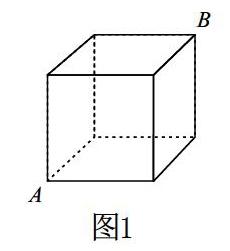
在初中數學教學中，“形”不僅具有直觀性，而且以形象的特征出現。然而，“形”也存在自己的不足，即缺乏定量優勢。如果教師能夠借助“數”的抽象優勢，輔之以“形”，既能將雜亂的“數”聚合，也能夠實現復雜“形”的簡單化，將圖形數字化。然而，“形”的數字化需要以觀察為基礎，把握“形”的特點，深入解讀其意義，這樣才能實現“形”向“數”的準確轉變，幫助學生建構空間觀念。如在“線段長短的比較”的教學中，一個重要的知識點是“兩點之間線段最短”，而基于這一知識點的問題也相對較多。如這樣一道練習：“一只小螞蟻要從一個正方體紙盒頂點A，經過正方體的表面爬到另一個頂點B（如圖1），哪條路徑最短，說出理由是什么？”

在教學時，筆者設計了四個環節。第一，看一看。要求學生仔細觀察這個正方體，設想這只螞蟻如何從A點爬到B點，路線一共有幾條，目測比較這幾條路線哪一條更短。第二，做一做。制作一個正方體模型，標出A點和B點，畫出幾條路線。第三，測一測。測量每一條路線的長度。第四，理一理。根據測得的數據，結合“線段長短的比較”的相關知識點，得出最短的路線。這個環節的教學，引領學生經歷了三個學習活動，第一個學習活動以觀察為基礎，引導學生通過目測和邏輯推理，根據正方體做出假設。第二個學習活動在學生得出假設的基礎上，引導學生建立模型，再將模型數字化，得出最短的距離線路。第三個學習活動是進行理論層面的概括，引導學生利用本課的知識點抽象概括結論。經過這個環節的教學設計，能較好地發揮“數”的優勢，引導學生借助“數”分析、推理，將物體的空間位置、線段的長短等表現出來。學生通過這一環節，利用數學知識解決實際問題的能力得到較好的發展，空間觀念也得到增強。

2.3? 數形兼顧，發展核心素養

“數”和“形”不是孤立的，而是互相補充、互相輔助的關系。目前，部分數學教師對“數”和“形”的關系認識還存在一定的局限性。只是簡單地將其定位在“以形助數”或者“以數解形”層面，這就需要數學教師轉變教學思想，從數形兼顧的視角，在數和形之間進行有機轉換，借助“形”的直觀形感受“數”的嚴密性，借助“數”的嚴密性感受“形”的直觀性，做到數形互見。如教學“一元一次方程的應用”中的行程問題時，有這樣一道題目：“甲乙兩人，分別從相距150千米的兩點A、B出發，甲的交通工具是自行車，乙的交通工具是摩托車，他們沿著同一條路勻速相向行使，甲的速度為每小時16千米，乙的速度是他的三倍，多長時間后兩人相遇？”

關于這一題的解答，教師可以先引導學生根據題目畫出數量關系圖（如圖2），表明兩人行走的數量，從而借助數量關系圖進行宏觀建構。這一過程是實現從“數”到“形”的轉變，引導學生對抽象的數量關系形成直觀的認識。緊接著，根據圖形揭示的數量關系，引導學生再從“形”向“數”的轉變，列出一元二次方程。通過這個過程，實現數形兼顧。

3? ?在數學教學中應用數形結合思想的注意點

一是引導學生提高作圖水平。在數形結合思想引領下，學生常常利用圖形的直觀性將抽象的數量關系表現出來，這就決定了圖形質量對解決數學問題的重要作用。目前，不少教師忽視了指導學生作圖，因此在數形轉化過程中，由于作圖不規范、不精準，作出的圖形使學生產生了誤導。所以，教師要基于數形結合思想，引導學生正確作圖，重點關注作圖的嚴謹性、規范性，從而使學生準確呈現數量關系，同時培養學生良好的數學學習習慣。

二是關注轉化的等價性。應用數形結合思想的一個重要環節是數形的轉化，即借助圖形揭示抽象的數量關系，并借助直觀的圖形建構數量關系。這一過程中需要進行科學、有效的轉化，才能使數形有機地呈現出來。然而，在轉化過程中，不少學生存在不等價轉化的關系，因此教師需要強化學生的等價轉化意識，避免出現不等價數形轉化，提升數形結合思想運用的效果。

三是引領學生二次建構圖形。圖形在數形結合中的作用是顯著的。在作圖過程中，想要將錯誤或者失誤降低到最少，教師需注重培養學生二次建構圖形的習慣。二次建構是一個綜合性反思和優化活動，即學生在作出相應的圖形后，再細致地觀察圖形，并對照題目，檢視作圖過程中是否存在錯誤和不等價現象等。在檢視圖形的基礎上，根據作圖的實際情況進行處理，如果存在問題，則及時優化，如果沒有問題再開展后續學習活動。

總之，數形結合思想是解決數學問題的重要思想之一。它不僅有助于降低學生學習數學的難度，做到化難為易、化繁為簡，而且有助于提高學生解決實際問題的能力，促進學生數學思想的形成。數學教師要根據數形結合思想的優勢，合理地選擇數形結合思想的常用形式，在數形互轉中發揮數形結合思想的優勢，全面促進學生數學核心素養發展。同時，要注意作圖的規范性、科學性，轉化的等價性等，幫助學生養成良好的習慣，全面提升學生解決實際問題的能力。

【參考文獻】

[1]茹春紅.數形結合思想在初中數學教學中滲透與應用[J].課程教育研究，2016（7）.

【作者簡介】

滕軻瑋（1994～），女，漢族，浙江溫州人，本科，二級教師。研究方向：數學與應用數學。