顧客策略行為下差異產品兩階段定價模型研究
馬 鵬,杜宛京,王海燕
(1.南京信息工程大學管理工程學院,江蘇 南京 210044;2.東南大學經濟管理學院,江蘇 南京 210096)
1 引言
目前,顧客策略行為的相關研究仍然是管理學界和相關企業關注的熱點問題,如Zara,H&M,以及Home Depot等大型零售商通過使用價格優化軟件來處理季末的產品,來應對顧客的策略行為。此外,在特定期限內零售商為自己出售的商品實行差價返還,也是應對策略性顧客的等待行為的一種途徑[1]。
市場競爭的日益加劇使得產品更新換代的速度越來越快,零售商在銷售期內也要根據市場情況及時改變定價策略來吸引顧客購買。例如,當新產品上市時,策略性顧客會選擇等待觀望而不是立即購買,那么在庫存壓力和產品更新換代的壓力作用下,零售商會選擇在第二銷售期對新產品進行折扣銷售,否則,產品的滯銷會使零售商面臨極大的損失。由于顧客策略行為的存在,零售商必須通過折扣降價來吸引消費者。而商家的頻繁降價已將顧客訓練的越來越具有策略性和選擇性,表現為顧客會預期產品降價而選擇等待一段時間購買折扣價格產品,以獲得更大的消費者剩余。因此,零售商為了銷售產品及獲得利潤最大化,定價決策時將顧客策略行為考慮其中就顯得非常重要。
本文針對季節性產品,研究基于顧客策略行為的定價決策,季節性產品具有銷售期相對較短,銷售期末的產品殘值較低等特點,因此常常采用正常銷售和季末降價結合的方式。分別考慮只存在高質量的產品,以及同時存在高質量和低質量兩種差異產品的情形。面對顧客的差異化需求,如何對差異產品進行定價成為零售商需要解決的首要問題,因為定價不當往往會導致消費者購買數量的減少,造成產品積壓,產生庫存浪費和資本占用。因此,考慮顧客對質量差異產品的策略選擇行為,給出零售商最優的定價決策,將是非常值得研究的問題。
國內外關于顧客策略行為的文獻很多,主要集中在以下兩個方面:(1)基于顧客策略行為的定價和訂貨量決策,以及供應鏈協調的相關研究,例如:李鋼和王勇[2]構建了一個由零售商和顧客群體組成的報童模型。Cachon和Feldman[3]研究了顧客策略行為下的價格承諾問題。Su Xuanming和Zhang Fuqiang[4]將顧客策略行為引入到供應鏈中,研究了顧客策略行為對供應鏈績效的影響。楊光勇和計國君[5]進一步研究了顧客策略行為對競爭性供應鏈績效的影響。王宣濤和張玉林[6]基于顧客策略行為的背景,研究了零售商具有公平偏好行為下的零售商最優決策及供應鏈協調問題。Ahmadi 等[7]研究了灰色市場和顧客策略行為下的批發價格契約和數量折扣契約。(2)基于顧客策略行為的動態定價的相關研究方面,官振中和任建標[8]將消費者的策略性行為和參考價格效應結合起來,研究消費者在歷史和預期價格下零售商的動態定價策略。Kremer等[9]通過理論和實驗,研究顧客策略行為對零售商動態定價策略的影響。Yan Bo和Ke Chenxu[10]研究了顧客策略行為下易逝品的兩種動態定價策略。關于策略顧客行為下的跨期定價決策相關的文獻有Su Xuanming[11],Liu Qian 和Zhang Dan[12],以及陳章躍等[13]。Su Xuanming[11]側重于內生性跨期需求下的動態定價決策,而Liu Qian和Zhang Dan[12]考慮顧客策略行為下兩個企業分別提供質量差異產品的動態定價競爭決策問題。陳章躍等[13]研究了顧客策略行為下的閉環供應鏈決策。本文主要考慮零售商銷售一個高質量產品,以及同時銷售高質量和低質量兩種產品時的定價決策等兩種情形。
關于差異產品定價決策的文獻較為豐富。Parlaktürk[14]考慮一個企業向策略性顧客銷售兩種質量差異產品,得到企業和顧客之間博弈的均衡策略。Liu Qian和Zhang Dan[12]考慮兩家企業提供垂直差異產品下的動態定價競爭問題。杜曉夢等[15]研究指出,消費者在接受和認知新產品時會面臨新產品產生的不確定性和感知風險。顏榮芳等[16]研究再制造閉環供應鏈差別定價決策,并對如何提高閉環供應鏈的效率提出意見。林欣怡等[17]發現制造商可以通過收益共享契約制定合適的批發價和收益共享比率來協調整個閉環供應鏈。曹曉剛等[18]研究了新產品與再制造產品的質量和價格競爭的決策模型。隨后,王文賓等[19]考慮新產品和再制造產品競爭環境下的逆向供應鏈獎懲機制。但是,以上文獻很少考慮顧客策略行為。
以上關于顧客策略行為的研究主要側重在定價和訂購量決策,供應鏈協調以及動態定價,但是很少有學者涉及差異產品的定價策略,而本文重點考慮兩個銷售期情形下差異產品定價決策問題。因此,本研究進一步豐富了顧客策略行為下的定價決策理論與方法。另一方面,關于現實意義方面,該研究為零售商在面臨策略性顧客時,確定最優的產品零售價格,獲得最大銷售利潤提供了決策支持。因此,研究策略性顧客行為下差異產品的最優定價決策對于生產或銷售單一產品或差異產品下企業的良好經營具有很好的指導作用,因此具有重要的現實意義。
本文在國內外關于顧客策略行為下差異產品的定價策略的研究和理論基礎上,考慮兩種情形,在第一類情形中,只存在高質量產品,根據顧客面對兩個銷售期的異質需求分別給出高質量產品的兩階段定價;在第二類情形下,市場上同時存在高質量和低質量兩種產品。此外,在兩種情形中,在第二銷售期都考慮產品的跨期折扣因子。
2 問題描述與假設
目前市場上的服裝等季節性產品,在經過一定的零售期后,其價格往往會大幅度下降。這主要是因為隨著時間的變化,該類季節性商品在消費者心目中的價值會逐漸降低,此時商家會被動或主動地降低價格來吸引消費者,從而進一步提高銷售利潤。零售商此時面臨的主要問題是,如何合理地調整價格,從而能夠更好地迎合消費者心中對于產品的期望值,并獲得利潤最大化。
考慮消費者支付意愿β,為了進一步刻畫消費者購買產品時的心理效用,建立相應的效用函數。顧客的效用函數由兩部分組成——支付意愿β和產品價格pi,j(i=1,2分別表示第一、二銷售期,j=H,L分別表示高質量和低質量產品)。在第一種情形中,市場上僅存在一種高質量產品,在經過一定銷售期后,由于產品并未全部銷售出去,因此零售商進行降價處理。此時消費者對于商品的整體效用評價會下降,把其下降的因子稱為δ,即跨期折扣因子,滿足0≤δ≤1(詳細解釋見假設4)。在另一種情形中,市場上同時存在高質量產品和低質量產品,并進一步地對其進行相應的價格調整,而消費者對于低質量產品的整體效用評價會低于高質量產品,為了方便模型的分析,在不失一般性的前提下,本文基于以下幾點假設:
假設1:piH、piL分別表示高質量和低質量產品的零售價格,cH、cL分別表示高質量和低質量產品的單位生成成本,qiH、qiL分別表示高質量和低質量產品的銷售量(i=1,2分別代表第一銷售期和第二銷售期)。
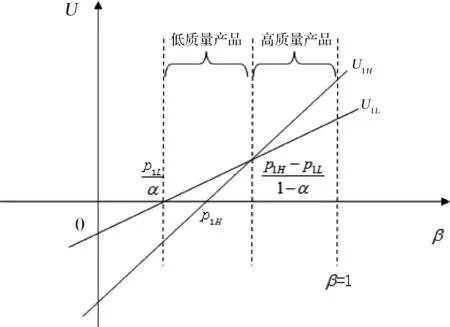
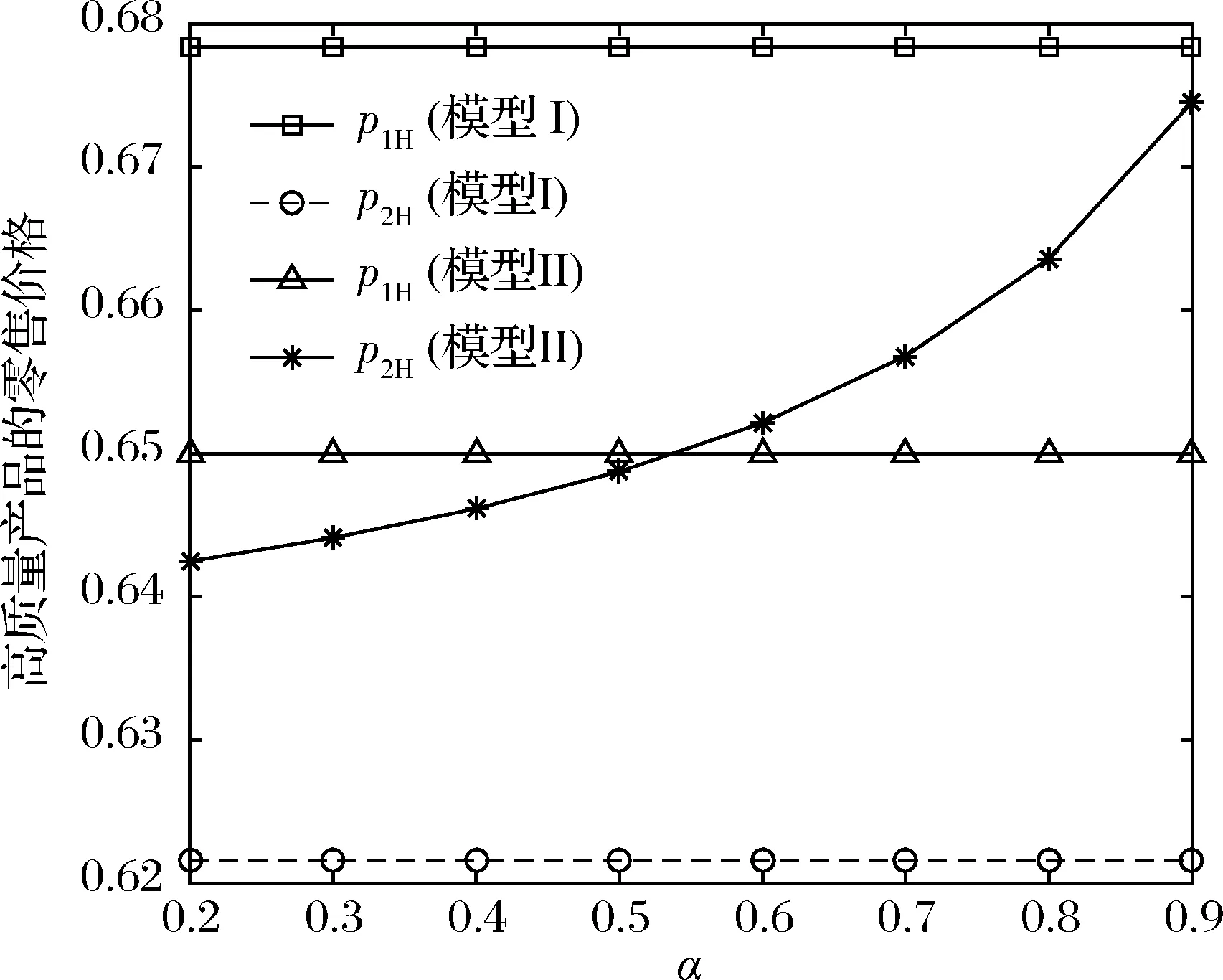
假設2:市場上該產品的潛在消費者總量為N,每個消費者只購買一件產品。當市場上只存在高質量產品時,消費者會選擇立即購買,或者等待一段時間再購買;當市場上存在高低質量兩種產品時,在產品銷售初期購買產品的消費者占總量的比例為r(0 假設3:消費者對高質量產品的評價或支付意愿為β,其服從區間[0,1]上的均勻分布,αβ表示消費者對低質量產品的評價或支付意愿,其中α表示消費者對低質量產品的評價是高質量產品的評價的一個比例(α也可理解為消費者對低質量產品的接受度),即α∈[0,1]。也就是說消費者對低質量產品的評價比對高質量產品的評價低。在第二類情形下,在第一銷售期,市場上同時存在高質量和低質量兩種產品時,顧客選擇購買高質量產品和低質量產品的效用函數分別為U1H=β-p1H,U1L=αβ-p1L。 假設4:類似于文獻Liu Qian和Zhang Dan[12], 以及陳章躍等[13],購買高質量產品時顧客效用的跨期折扣因子為δ,(0≤δ≤1)。δ可以理解為顧客的策略程度,δ越大表示顧客的策略程度越高。δ=0,意味著只要顧客得到正的剩余,則顧客就會立即購買。當同時存在高質量產品和低質量產品時,在第二銷售期,消費者心理對低質量產品的跨期效用評價會低于高質量產品,假設其跨期折扣因子為kδ,滿足0 考慮市場上只存在一種高質量產品,產品價格隨著時間的變化而變化,并且消費者對產品的效用也隨著時間進行折扣,顧客在銷售初期和銷售末期的效用分別為: U1H=β-p1H (1) U2H=δ(β-p2H) (2) 圖1 參數β與效用U的關系 由于β服從均勻分布,因此結合第一、第二銷售期的效用函數(1)和(2),可得高質量產品第一、第二銷售期的需求函數分別為: (3) (4) 高質量產品在第一銷售期和第二銷售期的利潤函數分別為: Π1H=(p1H-cH)q1H (5) Π2H=(p2H-cH)q2H (6) 因此,零售商銷售高質量產品在第一銷售期和第二銷售期的總利潤為: Π=Π1H+Π2H=(p1H-cH)q1H+(p2H-cH)q2H (7) 分別求式(7)關于p1H和p2H的一階導數,可得: (8) (9) 并且求Π關于p1H和p2H的二階偏導數,可得: (10) 由式(10),可得Π的黑塞矩陣為: (11) 聯立式(8)和式(9),可得: (12) (13) 將式(12)和式(13)分別代入式(3)和式(4)中,可得,高質量產品在第一銷售期和第二銷售期的最優銷售量分別為: (14) (15) 將(12)-(15)代入到式(7)中,可得零售商銷售高質量產品在第一、第二銷售期的總利潤為: (16) (2)高質量產品在第一銷售期和第二銷售期的最優銷售量都是關于δ遞減; (3)零售商利潤(Π)隨著跨期折扣因子δ的增加而減少。 由命題1可以看出,僅存在高質量產品的情況下,隨著跨期折扣因子增大,產品在第一銷售期降價變得快得多,產品在第二銷售期價格關于跨期折扣因子遞增。跨期折扣因子增大對產品的銷量來說是不利的,且整個產品的銷售利潤隨著跨期折扣因子的增大而減少。也就是說,跨期折扣因子對整個產品來說都是不利的。這是因為,當跨期折扣因子增大時,顧客的策略程度增大,使得更多的顧客選擇等待購買,而不是立即購買,從而顧客中選擇立即購買的人數減少,而選擇等待購買的人數增加,因而顧客策略行為對零售商是不利的。因此,零售商應該采取一些打折,差價返還等市場營銷策略來吸引顧客立即購買。 考慮市場上同時存在高質量產品和低質量產品,消費者會根據自身效用最大化在高質量產品和低質量產品之間進行選擇。此外,隨著時間的推移,顧客會在心理形成對高質量產品和低質量產品產生不同的跨期折扣因子δ和kδ。 (1)第一銷售期的模型 顧客對高質量產品和低質量產品在第一銷售期的效用函數分別為: U1H=β-p1H (17) U1L=αβ-p1L (18) 圖2 參數β與效用U的關系 圖3 參數β與效用U的關系 結合式(17)和式(18),可以得到高質量產品和低質量產品在第一銷售期的銷售量分別為: (19) (20) 其中,r為在產品銷售初期購買產品的消費者占總量的比例。 零售商銷售高質量產品和低質量產品在第一銷售期的利潤函數分別為: Π1H=(p1H-cH)q1H (21) Π1L=(p1L-cL)q1L (22) (2)第二銷售期的模型 高質量產品和低質量產品經過一段時間的上市后,消費者對于這種產品的熱情度會下降,會更理智的根據效用選擇購買高質量產品還是購買低質量產品,同時會在心理上形成一種跨期折扣因子δ或kδ(0≤δ≤1),此時,消費者對高質量產品和低質量產品的效用函數分別為: U2H=δ(β-p2H) (23) U2L=kδ(αβ-p2L) (24) (25) (26) 其中,(1-r)為降價后選擇購買產品的消費者占總量的比例。 零售商銷售高質量產品和低質量產品的利潤函數分別為: Π2H=(p2H-cH)q2H (27) Π2L=(p2L-cL)q2L (28) 聯合式(21)-(22),以及式(27)-(28),可得兩階段銷售期的兩個產品的銷售總利潤為: Π=Π1H+Π1L+Π2H+Π2L (29) 為使獲得的總利潤最大化,分別求式(29)關于p1H,p1L,p2H,以及p2L的一階偏導數,可得: (30) (31) (32) (33) 聯立式(30)-(33),可得兩種產品在第一銷售期和第二銷售期的最優零售價格分別為: (34) (35) (36) (37) 將式(34)-(37)代入到式(19)-(20),以及式(25)-(26)中,可得兩種產品在第一銷售期和第二銷售期的最優銷售量分別為: (38) (39) (40) (41) 將式(34)-(41)代入到式(29)中,可得高質量和低質量產品在第一、第二銷售期的總利潤為: (42) 對該情形下的最優解進行分析,可得命題2。 命題2:(1)在第一銷售期,高質量產品的零售價格p1H與顧客對低質量產品的接受度(α)無關,而低質量產品的零售價格p1L隨著α增大而增大。在第二銷售期,p2H,p2L都隨著α增大而增大。 (2)在第一銷售期,高質量產品的銷售量q1H隨著α增大而減小。低質量產品的銷售量q1L隨著α的增大而增大;在第二銷售期,高質量產品的銷售量隨著α的增大而減少,低質量產品的銷售量是隨著α的增大而增大。 證明: (k2cL+(-2cH+2cL+2)k+cL-2-2cH) 令H(k)=k2cL+(-2cH+2cL+2)k+cL-2-2cH,可得方程H(k)=0的兩個根分別為: 因此,p2L和p2H都隨著α增大而增大。 令 假設cH=0.3,δ∈(0.3,0.9),N=1000,且cL=0.2,r=0.4,以及α∈[0.2,0.9],考慮k=0.2,0.4,0.6,0.8,研究參數α對兩階段總利潤的影響。發現:給定一個k值,兩階段的總利潤隨著α的增大先減小后增大,也就是說α越大或者越小,即兩個產品差異較小或者兩個產品差異較大,這種情況對企業來說是最有利的。α越小(α=0.2),說明兩個產品質量差異越大,顧客在兩個產品之間選擇越來越固定,此時對零售商也是有利的,因為兩個產品之間的競爭很小。如果α越大(α=0.9),兩個產品質量差異越小,在第一銷售期,高質量產品的零售價格與顧客對低質量產品的接受度無關,而低質量產品的零售價格隨著α增大而增大。第二銷售期的兩個產品的零售價格都隨著α增大而增大,從而導致零售商的利潤增加。 此外,當兩個產品差異較小時,如果消費者在第二階段對低質量產品的跨期折扣因子相對較小(k=0.8),這樣對企業來說是最有利的;當兩個產品差異較大時,如果顧客在第二階段對低質量產品的跨期折扣因子相對較大時(k=0.2),這種情況對企業來說也是最有利的。 圖4 參數α對兩階段總利潤的影響 當α=0.2,0.4,0.6,0.8,研究參數k對兩階段總利潤的影響。發現:當兩個產品差異較大時(α=0.2,0.4),兩階段的總利潤隨著k的增大而增大。反之,當兩個產品差異相對較小時(α=0.6,0.8),兩階段的總利潤隨著k的增大而減小。對零售商來說,如果生產或銷售的兩個產品差異較大,則銷售期末兩個產品打折力度類似,這種策略對零售商來說比較有利。反之,如果生產或銷售的兩個產品差異較小,則銷售期末兩個產品打折力度差距較大,這樣策略對零售商來說更加有利。 圖5 參數k對兩階段總利潤的影響 下面分別研究參數α對模型I和模型II中高質量產品的零售價格及銷售量的影響。假設cH=0.3,cL=0.2,N=1000,r=0.4,δ=0.7以及α∈[0.2,0.9],圖6顯示: 模型I中的第一銷售期的零售價格高于模型II中的零售價格,而模型I中的第二銷售期的零售價格低于模型II中的零售價格。圖7顯示:當顧客對低質量產品的接受度增加時,模型II中的第一期和第二期的銷售量都會減少。這是因為,當α增加時,在顧客的心中,高質量產品和低質量產品的差異變小,從而兩個產品之間的競爭變大。 圖6 參數α對零售價格的影響 圖7 參數α對銷售量的影響 本文研究了基于顧客策略行為的差異產品兩階段定價模型。首先,分析了只存在一種高質量產品的兩階段銷售市場,找出其最優的定價決策,以及每一期最優的銷售量。研究發現:(1)高質量產品在第一銷售期的價格隨著跨期折扣因子增大而減小,高質量產品在第二銷售期的價格隨著跨期折扣因子增大而增大。(2)高質量產品在兩個銷售期的銷售量一致并隨著跨期折扣因子增大而減小。(3)高質量產品的兩階段銷售的總利潤也隨著跨期折扣因子增大而減小。 其次,研究了存在高質量和低質量產品的兩階段定價模型。發現:(1)第一銷售期的高質量產品的零售價格與顧客對低質量產品的接受度(α)無關,而低質量產品的零售價格關于α遞增。在第二銷售期時,高質量和低質量產品的零售價格都是關于α遞增。(2)在第一階段,高質量產品的銷售量隨著α的增大而減少,而低質量產品的銷售量隨著α的增大而增大。在第二階段,高質量產品的銷售量隨著α的增大而減少,而低質量產品的銷售量隨著α的增大而增大。 然后,數值分析了α和k對兩階段總利潤的影響,發現:(1)α相對較小或相對較大時,對零售商來說比較有利,也就是說產品差異較小或者差異相對比較大時,對零售商來說是比較有利的。 (2)如果零售商生產或銷售的兩個產品差異較大,則銷售期末兩個產品打折力度類似,這種策略對企業來說比較有利。(3)如果生產的兩個產品差異較小,則銷售期末兩個產品打折力度差距較大,這樣策略對企業來說更加有利。最后比較了模型I與模型II下高質量和低質量產品的零售價格與銷售量關于α的變化情況。3 模型構建與分析
3.1 零售商只銷售高質量產品的情形(模型I)
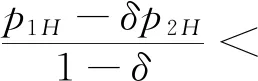
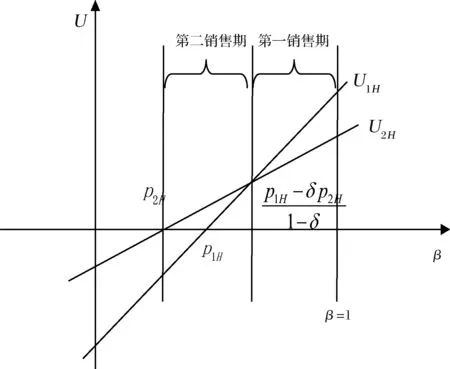
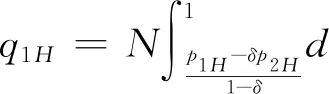

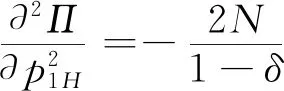
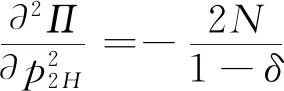
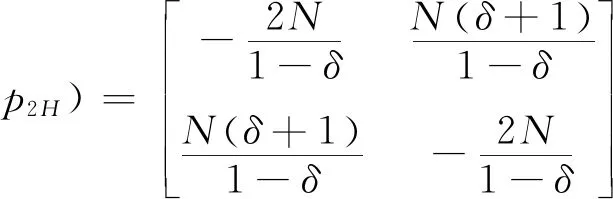
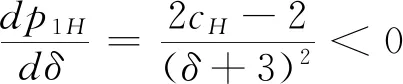
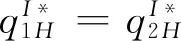
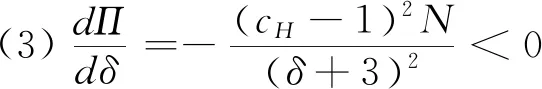
3.2 零售商同時銷售高質量和低質量兩種產品的情形(模型II)
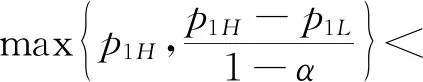

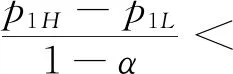
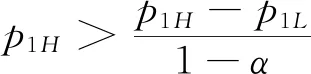

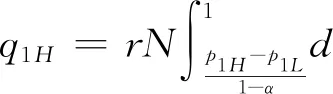
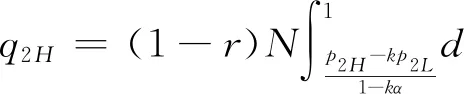
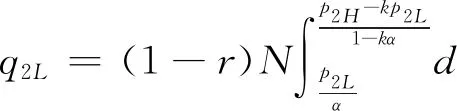
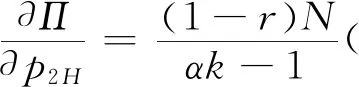
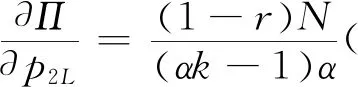
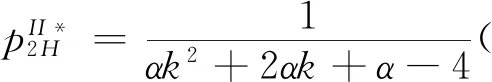
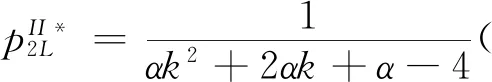

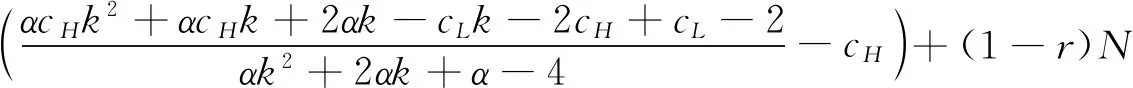
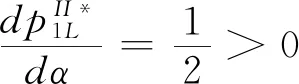
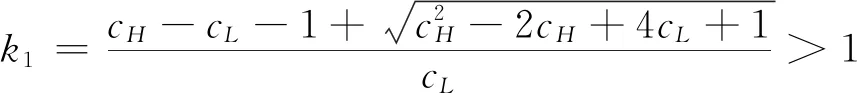
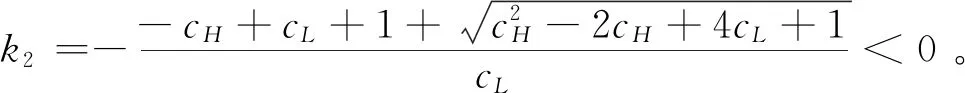
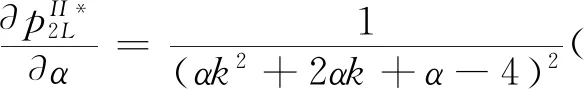
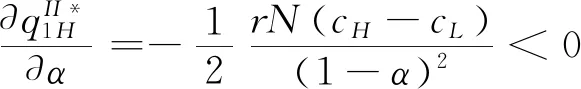
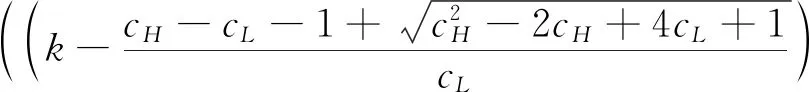
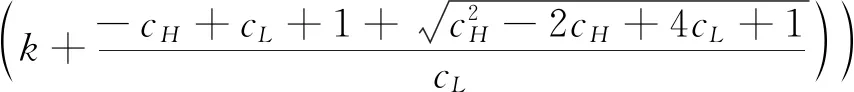
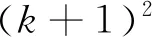
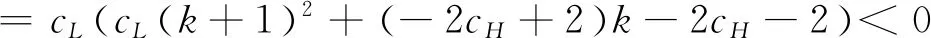
4 數值分析
4.1 參數α和參數k對兩階段總利潤的影響(模型II)
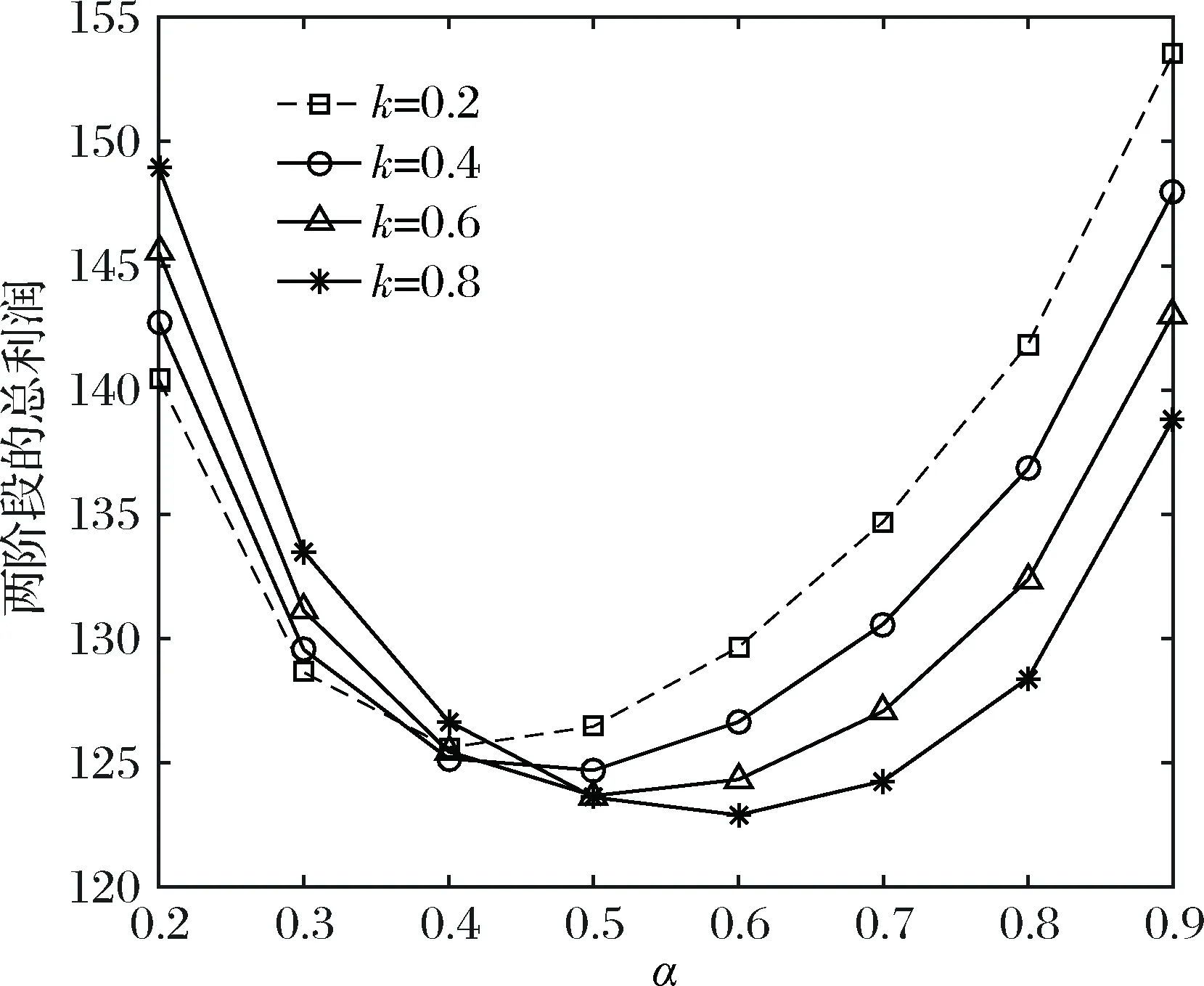
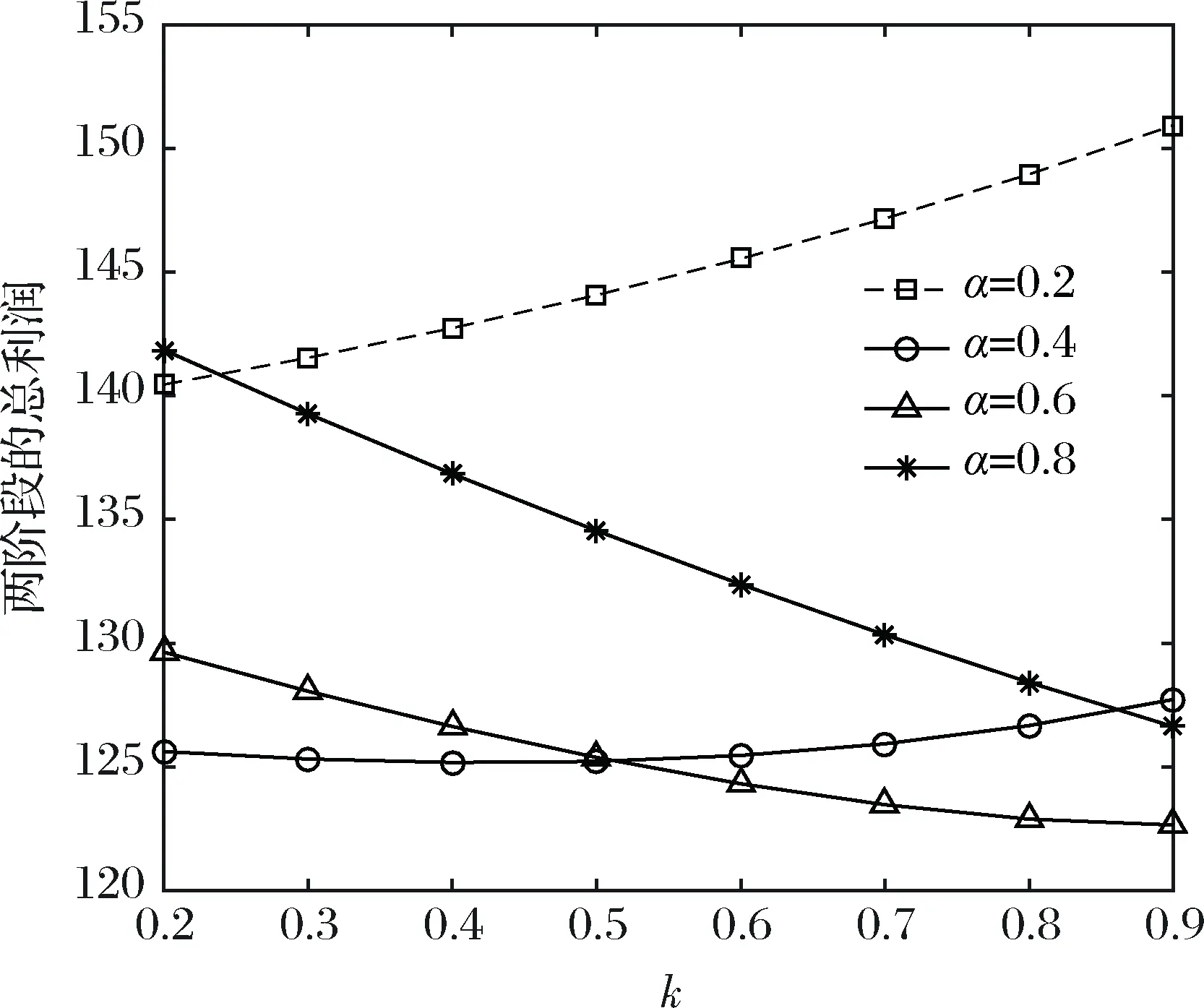
4.2 模型I與模型II的對比研究

5 結語

