基于滲流原理求解工程降水降落曲線的有限單元法

劉宜盈 趙 磊 李 冉

(煙臺大學土木工程學院，山東 煙臺 264005)

0 引言

對降落曲線的計算是計算基坑不均勻沉降的重要前提，基坑不均勻沉降嚴重時會造成周圍建筑物的開裂、變形。因此精確地計算降落曲線對實際工程有巨大的意義。

對降深等水文地質參數的求解的辦法有標準曲線對比法、直線圖解法、試驗法、切線法、微分圖解法、積分圖解法等。對于直線圖解法李如剛[1]提出了對實例進行穩定流放水試驗，用直線圖解法和水位恢復法計算降深等參數；鄒正盛等[2]依據最小二乘法建立自動配線法求解降深等參數，此類方法受到人為的影響較大，往往會產生較大的誤差。

相較于圖解法來說解析法更為簡潔，李華等[3]提出利用對定降深井流條件下隱含待求參數的流量函數擬合替代和流量比值關系，通過整理推導獲得了求解降深等相關水文地質參數的一元二次方程的解析法，但此類方法的工程量較大且測量誤差較大。另外針對非穩定井流的研究大部分學者都是從Theis基本方程出發進行求解：如文獻[4][5]的研究成果。穩定井流的研究則大都基于Dupuit公式，如文獻[6]～[11]的研究成果。但是由于Dupuit公式沒有考慮水流在入井時的水躍，因此在抽水井附近，實際漏斗曲線將高于Dupuit的理論曲線。

本文提出在滲流基本原理的基礎上利用三角形相似求解穩定潛水井的基坑降水降落曲線的有限單元法：在穩定滲流場(在降水達到控制點水位時)中利用能量損失率最小原理，求解出該滲流域真實的水頭分布位置，逸出點(降水后降水井井壁處的真實水位)的位置是確定的，因此可通過三角形相似求解該穩定滲流場在此狀態下各處的逸出點位置，即降落曲線的位置。計算結果表明該方法有較高的計算精度，另外采用該方法可以考慮水頭損失也彌補了裘布依公式未考慮水躍現象而導致誤差的缺點。

1 求解降落曲線

1.1 能量損失率最小原理

對于滿足條件的滲流域，求解滲流域中的水頭函數可以引入以下泛函[12]:

(1)

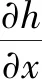
[K]{h}={f}

(2)

其中，[K]為n(未知節點水頭的數量)階總滲透矩陣;{h}為節點水頭列陣;{f}為自由項列陣。求解此線性方程組，即可求得各節點的水頭值，從而進一步計算降落曲線。

1.2 三角形相似求解降落曲線的方法

如降落曲線形成后，在曲線上下分為原水位線以上的無水部分、原水位線到降水后水位線之間的被疏干部分和降水后水位線以下的飽和土體。降水前水位線以上的土體沒有經歷降水的過程，因此其有效應力可視為不變，因此沒有沉降的產生；降水后原水位線和現水位線之間的土體在降水歷程中被疏干；降水后水位線以下色的土體在降水前后均位于穩定地下水位面以下，故而始終飽和[6,7]。在已知上游水位(降水前地下水水位)、下游水位(降水后降水井中的水位)以及滲出邊界(水躍區段)求解降水區域內各有限單元中水頭的分布，由逸出點(降水后降水井井壁處的真實水位)的位置出發，利用三角形相似求解該穩定滲流場在此狀態下各處的逸出點位置，即降落曲線的位置[13-15]。

當水位穩定后，降水井水位低于井壁水位，地下水在入井時的流速造成的水頭損失和入井后由水平運動轉為垂直運動的損失，會產生水躍現象[16]，本文利用阿布拉莫夫經驗公式[17]對水躍值Δh求解：

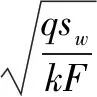
(3)

其中，q為單井排水量；F為面積，F=πdl(d，l分別為過濾器的直徑和長度，m，m2)；A為與過濾器有關的系數(網狀和礫石過濾器α=20，對縫隙和鐵絲過濾器α=7)。

然后利用文獻[18]的方法求解該滲流域的影響半徑，確定滲流域的水平距離。對該滲流域進行有限單元劃分如圖1所示。降落曲線將滲流域劃分為干區、濕區和過渡區，確定出過渡單元中過渡點的水位高度，將所有點連接起來即是降落曲線。

單獨取出圖1中被降落曲線穿過的單元，如圖2所示，降落曲線穿越單元的節點自左向右，自上而下分別為1,5,6,10,11,14,15，設其水頭及其位置水頭依次為(hi,zi)(i=1,5,6,10,11,14,15)，降落曲線與三角形單元邊長相交的節點，自左向右依次為(a,b,c,d,e)，其節點水頭和位置水頭依次為(hj,zj)(j=a,b,c,d,e)。即將求解降落曲線的問題轉化為求解降落曲線穿越單元的節點(a,b,c,d,e)的水頭，將這些點連接起來即是降落曲線。

過渡單元可以分為兩種類型：第一類是三角形單元中僅有一個節點在自由面以上，第二類是三角形單元中有兩個節點在自由面以上。以第一類單元為例求解過渡點的坐標，用線性插值法求出降落曲線與三角形單元的交點坐標：設所求邊的點為坐標點a，橫縱坐標用(xa,za)表示,邊兩端坐標(端點坐標利用能量損失率最小原理計算所得)分別表示為(x5,z5),(x6,z6)。則a點坐標為：

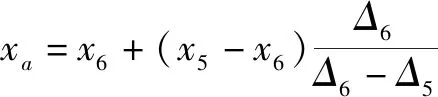
其中，Δ為水頭與縱坐標差值(在降落曲線上的點差值為0)。在求解三角形三條邊與降落曲線相交節點的水頭時，求法是相同，因此可以用這種方法求出每一個過渡單元的每一條邊上的降落曲線上的點。但是在程序編寫過程中，篩選各邊交點的方式不同[19]。這種方法在降水達到穩定時可直接定位出該逸出點狀態下的整個降落曲線的位置。該法不僅具有計算量少且精度高的優點，而且不需要多次迭代。另外采用該方法可以考慮水頭損失也彌補了裘布依公式未考慮水躍現象而導致誤差的缺點。

2 工程算例

工程概況[6,7]。該地鐵車站位于蘭州市七里河區馬灘村擬建工程場地，其基本概況為滲透系數取60 m/d，井成孔直徑1 000 mm，管井直徑800 mm，濾水管內徑500 mm，濾水井管內采用天然圓礫填料。地下水位埋深約為8.5 m～9.1 m，深基坑深約為16 m。基坑降水單井涌水量約為800 m3/d～1 200 m3/d。本次勘察其各自的力學指標見表1中的建議值。

觀測點分別命名為sw4，sw5，sw6，距離降水井分別為5 m，10 m，15 m。計算結果與裘布依方程的理論計算和實測值對比。在sw4，sw5，sw6觀測點本文計算結果與實測值的相對誤差分別為-3.0%，-5.7%，-6.9%，理論計算結果與實測值的相對誤差分別為-9.6%，12.1%，12.8%，結果表明文計算方法得到降深的結果與實測值更接近。

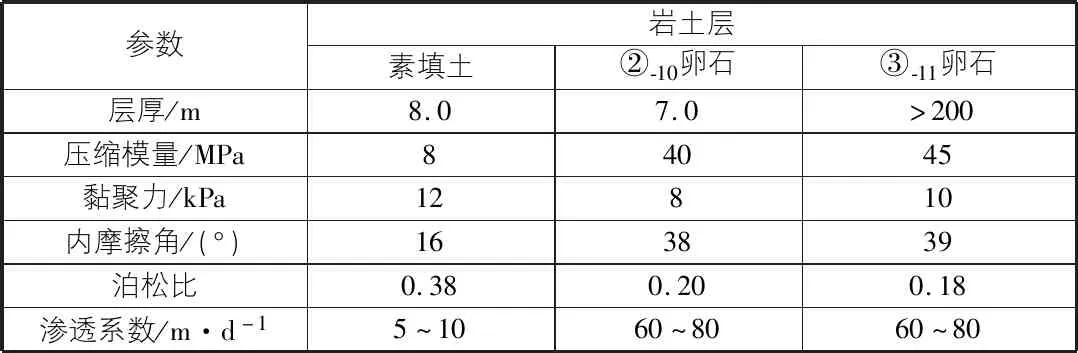
表1 擬建場地巖土層的物理力學參數

3 結論

本文在滲流基本原理的基礎上提出利用三角形相似求解穩定潛水井的基坑降水降落曲線的有限單元法。利用本文建立的計算方法計算了實際工程案例，得到的水位降深值與理論計算值和實測值作了對比，得到如下結論：

1)在穩定滲流場(在降水達到控制點水位時)中利用能量損失率最小原理，求解出該滲流域真實的水頭分布位置，逸出點(降水后降水井井壁處的真實水位)的位置是確定的，因此可通過三角形相似求解該穩定滲流場在此狀態下各處的逸出點位置，即降落曲線的位置。

2)該法不僅具有計算量少且精度高的優點，而且不需要多次迭代。