基于非線性規劃方法對結構抗震性能的研究
福州英華職業學院,福建 福州 350101
1 非線性規劃
非線性規劃是主要研究一個n 元函數在等式或不等式的約束條件下的極值問題,且目標函數和約束條件至少有一個是未知變量的非線性實函數。雖然大量的實際問題可以簡化為線性規劃、整數規劃、目標規劃等模型求解,但事實上,客觀世界中的許多問題都是非線性的,之所以用線性函數來刻畫多是出于簡化的目的。可是有些問題是不能夠進行線性簡化處理的,此時就需要建立非線性規劃模型。目標函數或者是約束條件只要不全是線性的,這類問題的研究就是非線性規劃方法的研究[1]。
然而對于非線性規劃問題的求解方法到現在為止仍沒有一種普遍、通用的方法,即適用于一般情況的方法。解決非線性規劃的最優化問題并不容易,因為它沒有像線性規劃那樣的通用算法,要針對實際問題的特點,建立相應的數學模型,結合非線性規劃中各種方法的使用范圍進行求解。目前在運籌學領域各種方法都有其特殊的使用范圍,這正是非線性規劃方法需要更深一步研究與發展的領域。
對于靜態的最優化問題,當目標函數或約束條件出現未知量的非線性函數,且不便于線性化,或勉強線性化后會招致較大誤差時,就可應用非線性規劃的方法去處理[2]。
2 建立非線性規劃模型
由于建筑結構的倒塌過程就是一個非線性過程,結構的建模、結構材料和構件之間的連接方式等都會對結構整體的非線性分析計算結果產生較大的影響。針對不同滯回特征參數對單自由度體系結構抗震性能的影響,確定結構抗震性能的主要因素主要有延性系數,次要因素有強化系數,而軟化系數以及剛度退化對單自由度體系的結構抗震性能幾乎無顯著影響,因此本文忽略軟化系數及剛度退化這兩個因素對結構抗震性能的影響,主要建立與單自由度體系結構抗震性能兩個主要因素的非線性規劃模型。
求解約束最優化問題的方法有無數多種,而懲罰函數只是其中一種較為簡便的方法。懲罰函數是將帶有約束的最優化問題轉換為無約束極小化問題來進行求解,通過一系列的懲罰因子求解目標函數的極小點用以逼近原問題的最優解,這樣便可以求解得出滿足所有約束條件的可行最優解[3]。
懲罰函數求解MP 問題是利用問題中的約束函數做出適當的帶有參數的懲罰函數,然后在原來的目標函數上加上懲罰函數構造出帶參數的增廣目標函數,把MP 問題的求解轉換為求解一系列無約束非線性規劃問題。
在求解無約束的優化問題的時候,對試圖要違反給定的約束條件的所有解給出相應的額外懲罰約束使得一系列的無約束優化問題的極小值點向給定的可行域不斷逼近,或在給定的可行域內搖擺移動,即極小點可能在可行域外部,也有可能在可行域內部,直至收斂到目標函數的最優解為止。
以采集的地震波記錄數據為基礎,利用懲罰函數法建立非線性規劃模型,并進行求解和分析延性系數、強化系數兩個因素對結構抗震性能的影響程度。利用懲罰函數方法,對結構抗震性能的主要因素進行分析,主要是確定罰因子,罰因子的大小直接導致問題的求解結果發生很大的變化。由于大的懲罰參數帶來的困難,因此應用懲罰函數的大部分算法都使用一系列逐漸增大的懲罰參數值,對于懲罰函數的每一個新值,以前一個選取的參數值相應的最優解為開始點[4]。如何確定罰因子,對利用罰函數法求解任何非線性規劃問題都至關重要。
3 數據分析
本文通過翻閱建筑結構抗倒塌學術研討會統計的數據,以采集的地震波記錄數據為基礎,主要是基于Imperial Valley-06及Nahanni 的地震波數據,得到地震波記錄及條幅系數統計表、簡化模型參數表,見表1、表2。本文著重分析延性系數及強化系數對單自由度體系結構抗震性能的影響程度。
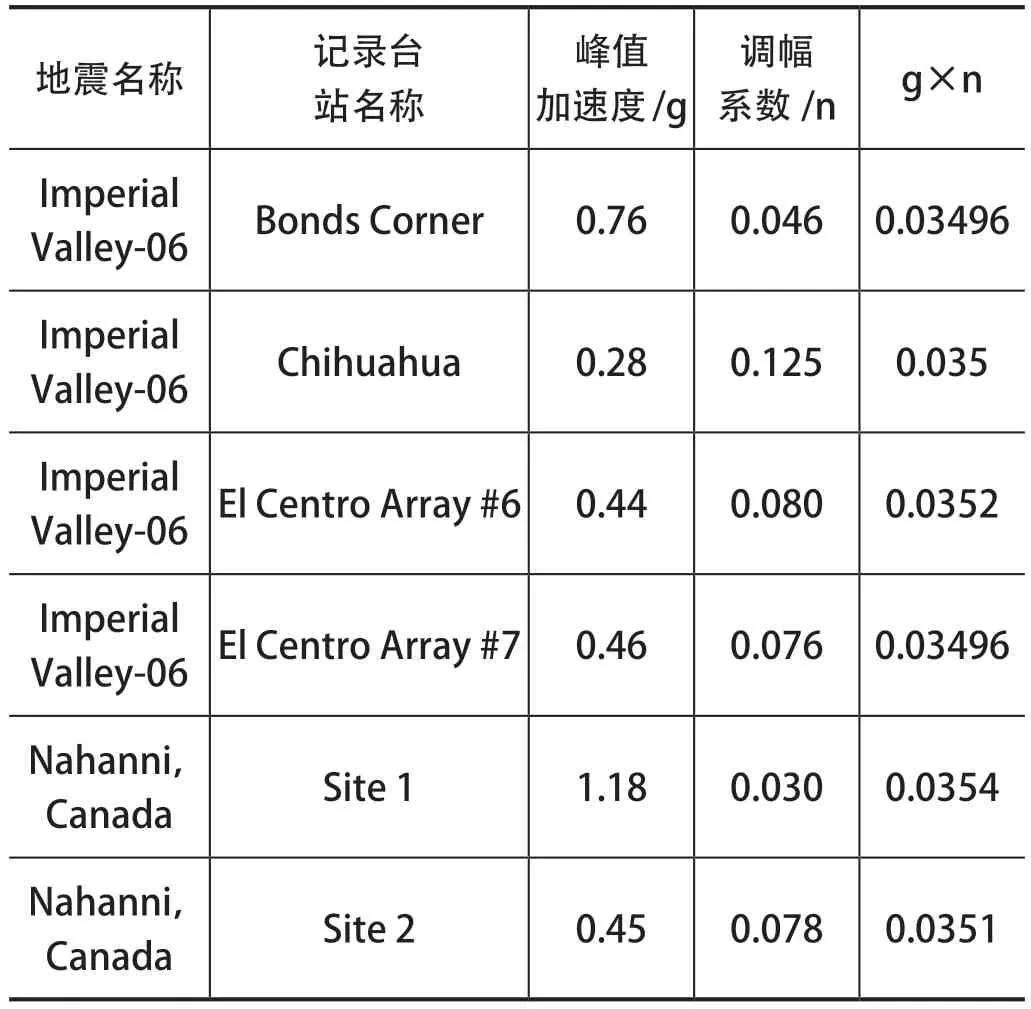
表1 地震動記錄以及調幅系數統計表
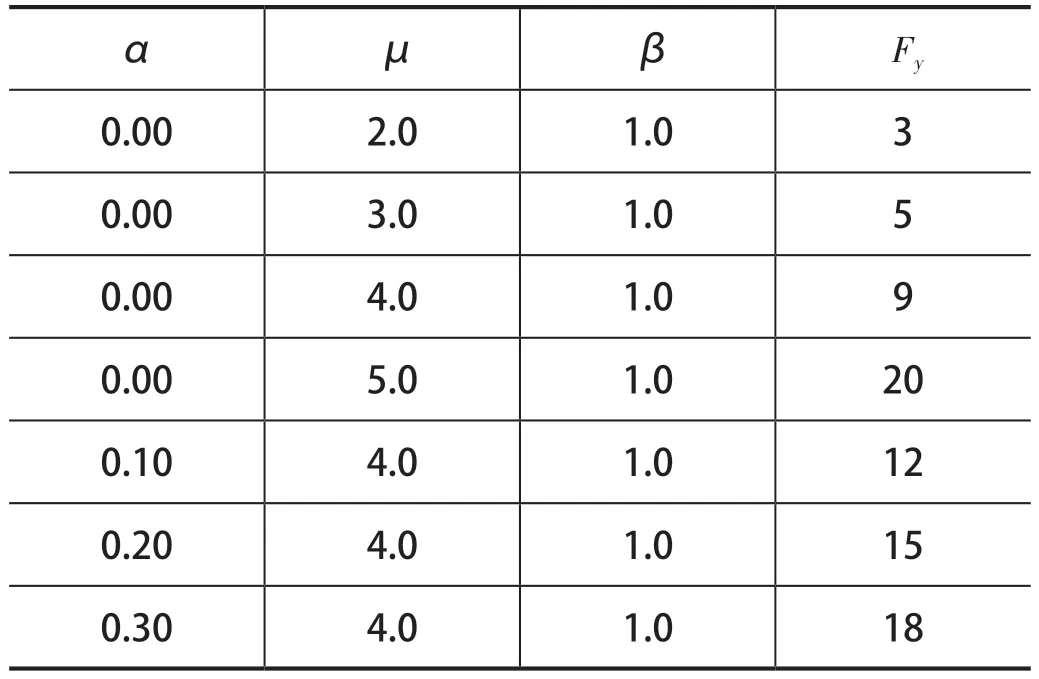
表2 簡化模型參數表
骨架曲線中包含以下參數:強化系數α,軟化系數β,屈服剛度KS,延性系數μ,屈服承載力Fy,屈服位移Dy,由相關研究數據得到延性系數μ=4.0 的單自由度體系結構,其骨架曲線如圖1、圖2 所示。
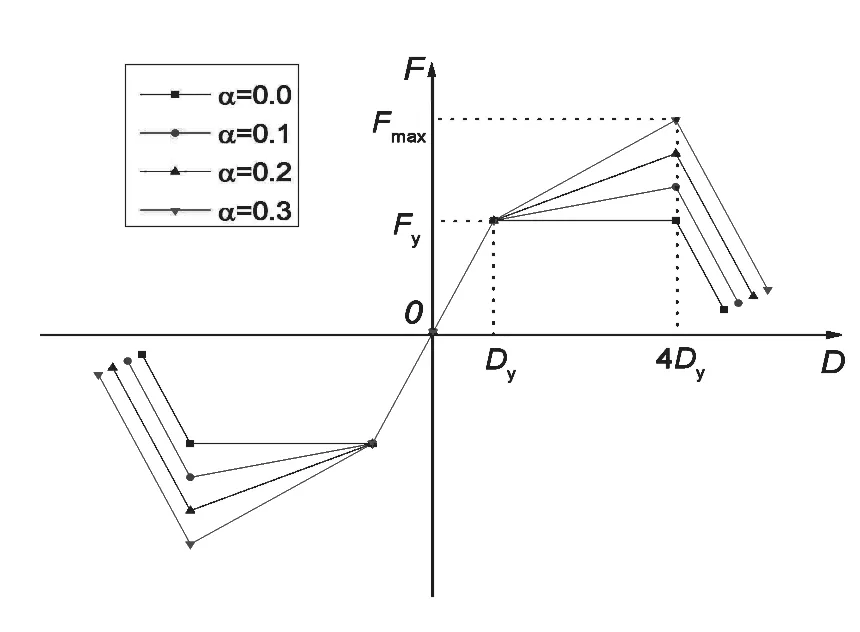
圖1 不同強化系數的骨架曲線

圖2 不同延性系數的骨架曲線
由地震動記錄以及調幅系數統計表可以發現:在同一地震中峰值加速度與調幅系數相乘之后存在一個相近的數值,此數值越接近則記錄的數據越準確,可作為實驗數據進行研究分析。
依據簡化模型參數表,結合圖1、圖2 的骨架曲線可以看出當強化系數α 固定時,延性系數μ 越大,屈服承載力Fy最大值也越大;當延性系數 μ 固定時,強化系數α 越大,屈服承載力Fy最大值也越大,但是二者的增加幅度卻有大不同。
決策變量X=(x1,x2)T,其中x1為延性系數,x2為強化系數,y 為屈服承載力。根據表2、圖1、圖2 數據可以發現決策變量與屈服承載力的關系,得到的方程如下:
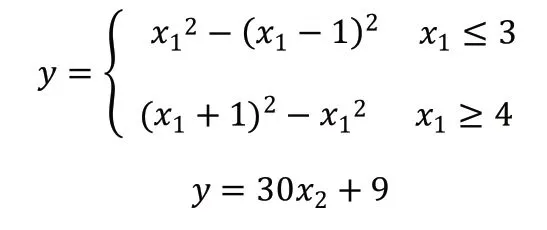
利用懲罰函數繼續對單自由度體系結構抗震性能進行進一步的驗算分析,使得理論數據在結構抗震中能得到實際的應用。結構抗震性能可以通過屈服承載力及屈服位移來確定,懲罰函數是求解目標函數的最小值,即可選取目標函數為屈服位移最小,則表示結構抗震性能優良。屈服位移主要由延性系數、強化系數、屈服承載力決定,經過行業專業人員的預測,其中延性系數對屈服位移的影響程度為4x12,強化系數對屈服位移的影響程度為(30x2)2,屈服承載力對屈服位移的影響程度為-17y。
由此建立了如下的數學規劃模型:
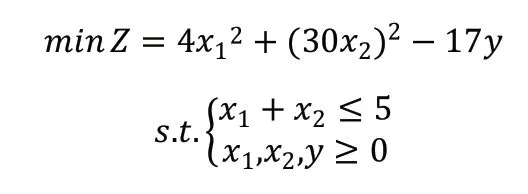
對目標函數進行相應的變換,則簡化后的數學模型如下:

利用懲罰函數求解數學模型,當k 無限增大的時候yk是從問題可行域外部趨于它的最優解y*=9.25。而后根據y*計算出延性系數x1=5.125,強化系數x2=0.0083。
4 結論
由計算結果可以看出當延性系數為5.125,強化系數為0.0083,屈服承載力為9.25,此刻屈服位移最小,表示結構抗震性能達到最優狀態。在本文假定的各個約束條件下,延性系數與強化系數是同等考慮的,但是延性系數對結構抗震性能的影響最為顯著。
通過分析相關數據指標,對Imperial Valley-06 及Nahanni的地震波數據進行合理的分析,利用懲罰函數建立相應的數學模型并進行求解分析。探析結構抗震性能后,發現應盡可能的考慮在一定范圍內增大延性系數,減小強化系數,這樣才可以很好的保證結構的抗震性能。

