雙車廂兩棲車靜水直航下的水動力性能研究

王少新，金國慶，王涵，孫蕊，劉賀

(1.大連理工大學 船舶工程學院，遼寧 大連 116024；2.大連馭海佳藝咨詢科技有限公司,遼寧 大連 116000；3.哈爾濱第一機械集團有限公司，黑龍江 哈爾濱 150056)

0 引言

水陸兩棲車依靠車輪或履帶實現陸地上行走，依靠推進式螺旋槳或噴水推進裝置實現水上航行，無論在國防還是民生經濟領域都有較大的市場需求，如軍事上可作為突擊登陸、巡邏運輸和資源補給等；在民用上可用于抗洪救災、運送人員和物資等[1-2]。兩棲車在陸地上的行進過程與普通車輛無異，但在水中航行時受水動力環境影響較大，如存在對航行速度的要求，由于兩棲車屬于鈍體結構物，流線型較差，導致水阻力大，此時必須考慮車輛外形設計以減小水阻力，以及采用高效的推進設備實現航速要求。此外，海洋環境的惡劣對兩棲車輛的穩性和耐波性提出了更高要求[3]。近年來，為提高兩棲車的運載能力，有關單位研究開發了某型號雙車廂水陸兩棲車，車身長18.5 m，最寬處寬度5.2 m，設計吃水線距離輪轂中心線1.472 m，在靜水正浮狀態下橫傾角和縱傾角均為0°；滿載排水量約為88 t，前車廂排水量38 t，主要布置車用行進設備和駕駛人員，后車廂排水量50 t，主要用于存放運載貨物與人員；前后兩車廂中間采用鉸接形式連接，鉸接設備安裝在水密箱體內部；前后車廂各布置兩個推進裝置，用以克服雙車廂存在的水阻力；對于兩棲車，為防止出現大幅度埋首現象(該現象通常會導致兩棲車在水中縱傾角太大而傾覆)，防浪板[4]的設計安裝必不可少。本文研究的兩棲車模型選用具有一定厚度的方形板作為防浪板，安裝角度為35°.雙車廂的設計可大幅改善兩棲車輛的運輸能力，本文研究的兩棲車計算簡化模型主視圖和俯視圖如圖1所示。基于該背景，本文主要基于數值方法對雙車廂兩棲車的水動力性能進行仿真研究，以服務于工程設計。

圖1 雙車廂兩棲車計算簡化模型Fig.1 Simplified model of a double-carriage amphibious vehicle

對于兩棲車水中阻力與運動性能的測量，傳統做法是基于相似理論，采用縮尺模型進行拖曳水池試驗[5]，該試驗方法的可靠性較高，但是試驗成本較高、周期較長，大量的工況無法全部通過試驗完成。近年來，隨著計算流體力學(CFD)的發展，船舶運動與水動力性能計算的精度大幅提高，此外，計算機處理數據性能的提升也進一步推動了CFD方法在船舶工程中的實際應用。李玉良等[6]采用CFD多相流模型對不同車體方案在不同速度下的水上性能進行了對比，結果表明適當增大車輛縱傾角和在裙板上增加平板薄翼有助于減少阻力。徐一新[2]基于Fluent軟件對兩棲車的黏性繞流場進行了數值模擬，研究了車體尾部形狀對流場的影響，證明了行駛環境的改變對阻力的影響。萬曉偉等[7]基于k-ε(k為湍流動能，ε為湍動能耗散率)湍流模型和流體體積函數(VOF)方法實現了良好的兩棲車水上阻力預測。袁瀟龍等[8]采用CFD方法研究了防浪板對兩棲車水上航行性能的影響，驗證了新型防浪板的減阻效果。酒永勝[9]基于CFX商業軟件，采用Level Set方法模擬自由液面并采用剪切應力傳輸(SST)k-ω湍流模型計算兩棲車迎浪直航運動，分析了航速、波高和波長等要素對兩棲車航行姿態和受力特性的影響。劇冬梅等[10]同樣采用CFX軟件和多相流模型研究了縱傾角對兩棲車阻力特性的影響，計算結果和試驗吻合良好，結果表明隨著航速的增加，車體縱傾角的適航范圍變小，但對阻力的影響幅度變大。彭錕[11]和彭錕等[12]基于CFD技術結合代理模型，對兩棲車輛外形減阻優化進行了研究，得到了車體最優航行傾角、最優長寬比等設計方法，此外還研究了加裝尾翼板對航行阻力的影響，結果表明在低傅汝德數時加裝尾翼板可以起到很好的減阻效果。趙彬等[13]采用k-ε湍流模型和動網格技術，研究了兩棲車在靜水直航中的航行姿態變化規律，模擬結果與試驗吻合較好。鄭翔玉等[14]采用Fluent商業軟件研究了車輪收放前后對兩棲車減阻增速的影響，結果表明車輪收起后，車輛水上行駛阻力減小，增速效果明顯。蔡宇峰等[15]基于可實現的k-ε湍流模型、VOF方法和重疊網格技術建立了兩棲車三維非定常數值模型，并與試驗結果進行了對比，驗證了該模型的有效性。王麗麗等[16]同樣采用上述數值模型研究了尾壓浪板的減阻效果，且表明VOF方法捕捉到的自由液面與實際情況較為相符。孫旭光等[17]基于CFD技術提出了以改進疊模為技術路線的形狀阻力分離方法，計算結果與拖曳模型航行阻力試驗結果基本吻合，建議在兩棲車的總體設計中應力求優化車尾形狀使得車后部收縮平緩，同時增大長寬比以減小形狀阻力；車首優化時應改善與水流交界的入流角，使其盡量小以達到減小車輛興波阻力的效果。

綜上所述可知，近年來國內對兩棲車的水動力性能研究主要集中在采用商業CFD軟件計算兩棲車在靜水下的阻力和快速性等問題，以及通過大量數值模擬研究影響兩棲車水動力性能的各要素并提出具體的優化方案。研究對象主要集中在單車廂兩棲車的靜水航行運動，而新型網格技術如重疊網格的模擬計算則較少。由于雙車廂兩棲車可大幅提升貨物運載能力，但國內外缺乏對此類新穎的兩棲車水動力學性能的設計研究，本文采用CFD方法和重疊網格技術對雙車廂的實尺度水陸兩棲車在靜水下的直航運動響應進行數值模擬，建立多體運動的數值仿真模型，雙車廂之間采用具有3自由度的球形鉸接點進行連接；研究車體總阻力、縱搖和垂蕩等運動性能以及球鉸對前后車體在3個方向的作用力。數值計算與拖曳水池試驗的總阻力結果基本一致，表明該數值模型可以較好地預報雙車廂兩棲車的水動力性能和運動狀態；由靜水海況下的計算結果可以發現，總體上雙車廂兩棲車的縱搖角度保持在1°以內，車體縱穩性能優良。

1 CFD模型設置

1.1 物理模型設置

本文借助CFD商業軟件STAR-CCM計算雙車廂兩棲車在靜水直航下的水動力性能。假定計算域中的水和空氣均為不可壓縮流體，控制方程主要包括質量守恒和動量守恒方程。采用有限體積法(FVM)進行空間離散，采用分離流模型和隱式非定常求解器求解流體方程。湍流模型選擇適用于復雜幾何外部流動問題求解的可實現k-ε湍流模型。自由液面的捕捉和模擬采用VOF方法[18]，通過在入口邊界給定流速和液面位置的設置來模擬靜水自由液面。對于靜水運動問題，用流速代替車體航速，以保證車體模型在有限區域內完成較長時間的運動模擬。

1)不可壓縮流體質量守恒方程

(1)

式中：vx、vy、vz分別為流體速度矢量v在x軸、y軸、z軸上的速度分量。

2)動量守恒方程(Navier-Stokes方程)

(2)

(3)

(4)

式中：ρ為流體密度，是1個常數；p為流體微元體上的壓力；div為散度符號；μ為動力黏性系數，是1個常數；grad為梯度符號；fx、fy、fz分別為微元體上x軸、y軸、z軸方向的質量力，質量力只有重力，且z軸方向豎直向上，因此fx=0、fy=0、fz=ρg，g為重力加速度。

兩棲車的6自由度運動模擬利用動態流體與固體相互作用模塊(DFBI)求解完成。使用該方法求解需指定雙車廂兩棲車為多體運動，該運動模式可以確保前車體和后車體之間通過球形鉸接(見圖2)存在相互耦合作用。球形鉸接是一種具有3個轉向自由度的裝置，通過球鉸相互連接的物體無相對位移運動，只存在相對角度的變化，適合作為兩棲車前后車體的連接裝置來模擬雙車廂耦合運動。流場對前后車廂的作用力均可以通過球鉸聯系起來。因此，單個車廂主要受到重力、流體水動力和鉸接力三者的作用。兩棲車運動過程中存在縱蕩、橫蕩和垂蕩3種平移運動以及橫搖、縱搖和艏搖3種旋轉運動，因此必須指定前后車體各自的質量和慣性矩，以及兩車廂的吃水和重心位置。本文所有模擬只研究垂蕩和縱搖2個方向的自由度，對于橫搖運動，由于車體形狀對稱設計且方形系數較大，其橫搖角度較小，不對其橫搖運動進行分析。因此必須控制其他3個自由度的運動狀態。在實際靜水直航運動中，縱蕩速度是固定的，因為數值模擬的計算域大小和網格數量有限，數值計算采用大小相等、方向相反的流體運動代替車體的縱向運動，并添加與運動狀態有一定函數關系的外部作用力，以保證縱蕩位移在計算穩定段保持在平衡位置；實際靜水直航中兩棲車按照一定航線行駛，其橫向運動幾乎不變，因此在數值計算過程中引入了控制策略，添加外部作用力，以保證橫蕩位移在計算穩定段保持在平衡位置；對于艏搖運動，兩棲車實際直航運動中可通過控制轉向裝置舵使車體按固定直線行駛，因此在數值計算中通過施加外部作用力矩，以保證艏搖角度在計算穩定階段保持在0°位置。

圖2 雙車廂兩棲車計算簡化模型Fig.2 Simplified model of a double-carriage amphibious vehicle

1.2 網格劃分和邊界條件設置

本文計算采用重疊網格技術[19-20]，計算域分為背景流域和重疊網格區域兩部分，其中重疊網格域又可以分成前車廂重疊網格域和后車廂重疊網格域兩部分，兩兩之間都設有重疊網格交界面。使用3套網格進行網格劃分，總網格數為407萬，各網格區域網格數量如表1所示。網格劃分需考慮當地流場變化是否劇烈以及物面的復雜程度，因此本文研究的網格劃分方法需在全局網格的基礎上對部分區域進行網格加密操作。

表1 各區域網格數量Tab.1 Quantity of grid in each region

自由液面對計算結果的影響非常大，因此對自由液面處網格進行了加密，尤其是尾流興波區域進行重點加密；車體物面網格，尤其是復雜位置如防浪板、履帶、車輪以及側浮箱的形狀變化劇烈，需要單獨設置加密區域進行網格加密；車體表面邊界層網格對摩擦阻力的計算影響較大，本文計算選取y+=80進行計算，參數y+是CFD中用來計算物面處第1層網格厚度的無量綱數，在計算過程中需要根據所選擇的湍流模型、流體屬性、物體運動參數等因素綜合確定，計算選取的邊界層總厚度為5 mm；此外，物面附近流場變化比較復雜，因此需要對物面周圍網格進行加密；考慮到物面周圍網格尺寸與流域網格基礎尺寸之間差異較大，需在背景計算域內設置網格過渡區域進行網格逐層過渡細化，一般網格以2倍變化率進行過渡，但要注意最好保持過渡區域的網格尺寸和重疊區域的網格尺寸一致。本文網格劃分采用自動網格劃分方式，最終的網格劃分截面示意圖如圖3所示。

圖3 網格劃分示意圖Fig.3 Schematic diagram of meshing

邊界條件的選擇對計算結果也有十分重要的影響。本文研究的流域邊界條件由5個速度入口和1個壓力出口組成，對于速度入口均給定兩棲車航速，方向與車體運動方向相反；車體物面設置為無滑移壁面邊界條件；自由液面采用VOF方法設置靜水面。為了減弱由于出口數值反射造成的回流現象，在距離壓力出口6 m范圍內采用VOF波阻尼方法進行消波，具體的邊界條件設置如圖4所示，圖中L為兩棲車的車身長度。

圖4 邊界條件設置Fig.4 Setup of boundary conditions

圖5 數值模擬與拖曳試驗結果對比Fig.5 Comparison of numerically simulated result and model towing test result

綜上所述，本文使用基于有限體積法的CFD流體計算軟件STAR-CCM+，采用可實現的k-ε湍流模型和重疊網格技術建立了以球鉸方式連接的雙車廂兩棲車多體運動數值模型。基于該數值模型計算了6 km/h、8 km/h、10 km/h、12 km/h、13 km/h共5種航速下的靜水總阻力，并與船模拖曳水池的試驗結果進行了對比，如圖5所示。拖曳試驗在大連理工大學船模拖曳水池完成，試驗樣機如圖6所示，模型試驗的結果根據傅汝德數相似條件換算到實尺度上。由圖5可以看出，數值計算的總阻力與試驗結果基本一致，低航速下的相對誤差較大。考慮到兩棲車的履帶等復雜結構導致建模過程存在簡化，本文研究的計算誤差仍在合理范圍內，因此該模型可以用于兩棲車的水動力性能計算。

圖6 兩棲車模型拖曳試驗Fig.6 Towing test of an amphibious vehicle model

2 雙車廂兩棲車水動力性能研究

兩棲車在靜水中的直航運動模擬需采用VOF方法來建立自由液面，需指定氣體與液體兩相流體屬性、水線位置、流速大小和方向。本文研究計算了兩棲車在靜水下的阻力、縱搖、垂蕩運動以及球鉸3個方向的受力情況。圖7所示為典型工況12 km/h航速下兩棲車的阻力系數變化時程曲線，本文均選取計算穩定段內10 s的計算結果平均值進行對比研究。車體航速包括6 km/h、8 km/h、10 km/h、12 km/h、13 km/h共5種，各航速下水動力性能的計算結果分別如圖8～圖10所示。對于低航速工況，兩棲車的運動性能計算可以更快速地達到穩定狀態。此外，本文以典型工況12 km/h航速為例，研究了球鉸在x軸、y軸、z軸3個方向對前后車體的作用力情況，其中x軸方向為車尾指向車頭的縱向方向，y軸方向為沿車寬的橫向方向，豎直向上為z軸方向(見圖4坐標系)。計算結果的時程曲線如圖11～圖13所示。

圖7 12 km/h航速下阻力系數時程曲線Fig.7 Drag coefficient versus time at 12 km/h

阻力系數的計算公式為

(5)

式中：Cd為兩棲車的阻力系數；Fd為兩棲車總阻力；S為兩棲車水下的濕表面積。

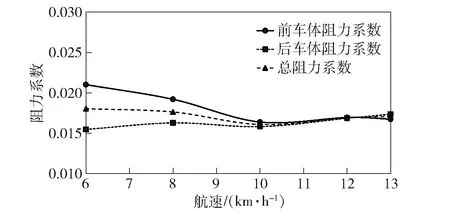
圖8 阻力系數計算結果Fig.8 Calculated results of drag coefficients

圖9 縱搖運動計算結果Fig.9 Calculated results of pitching motions

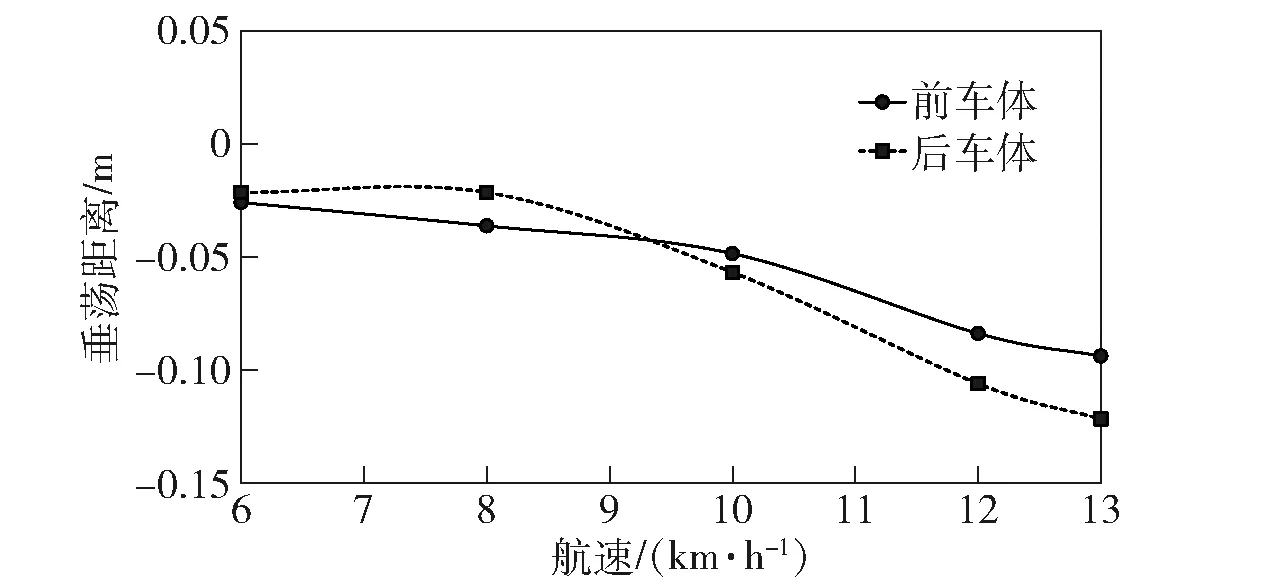
圖10 垂蕩運動計算結果Fig.10 Calculated results of heaving motions

圖11 12 km/h航速下球鉸x軸方向作用力時程曲線Fig.11 Applied force of spherical joint in x-direction at 12 km/h

圖12 12 km/h航速下球鉸y軸方向作用力時程曲線Fig.12 Applied force of spherical joint in y-direction at 12 km/h

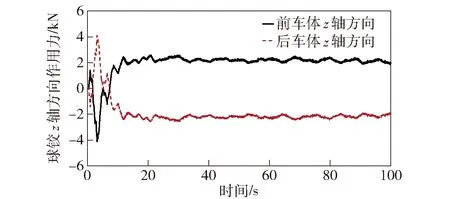
圖13 12 km/h航速下球鉸z軸方向作用力時程曲線Fig.13 Applied force of spherical joint in z-direction at 12 km/h

由圖8可知，兩棲車的阻力系數是較大的，原因主要是車體型線是非流線型的，方形系數大，且水下濕表面積較大，導致產生較大的壓差阻力和摩擦阻力。由圖9可知，兩車廂在球鉸連接的情況下通常保持中垂或中拱狀態，以埋首方向為縱搖正方向，低航速下前車體埋首而后車體仰首，高航速下前車體仰首而后車體埋首，原因是高航速下傾斜的防浪板提供了較大升力。此外，總體上可以看出前后車體的縱搖角度均保持在1°以內，車體縱穩性能優良。由圖10可知，兩棲車航速越高，車體平均下沉深度越大，且前后車體的垂蕩值相近，原因主要是周圍流速的增大導致車體上下壓差變大，因此車體吃水在高航速下會增加。

由圖11～圖13可知，靜水直航穩定狀態下，以一定控制策略施加外力(螺旋槳推力)作用時，球鉸在x軸方向對前后車體的作用力可以達到很小。在實際兩棲車航行時，因為前后車體自身均配置有推進器，所以可通過調節各自推進器的轉速，以使得鉸接裝置在縱向受力最小；在y軸方向的作用力在穩定段的波動幅值較大，原因可能是前后車體的橫蕩運動不同步造成的；在z軸方向的作用力較大，主要是前后車體埋首方向不一致，導致兩棲車總體上出現中垂或中拱現象引起的，工程中需重點考量z軸方向作用力對球鉸的影響。需要說明的是，兩棲車在回轉運動中水平方向(x軸和y軸方向)會產生較大的作用力，此外，兩棲車在波浪中的運動對球鉸垂向(z軸方向)作用會更大，因此實際工程中需要結合多種運動狀態和海況條件來設計鉸接裝置。

3 結論

本文基于CFD方法和重疊網格技術建立了以球鉸方式連接的雙車廂兩棲車多體運動數值模型，采用VOF和DFBI方法實現了兩棲車在靜水海況下的多自由度直航運動狀態模擬，并與兩棲車樣機模型的拖曳試驗結果進行了對比；獲得了兩棲車的阻力、縱搖角、垂蕩距離和球鉸3個方向受力數據并進行了比較。得出主要結論如下：

1)數值計算與拖曳水池試驗的總阻力結果基本一致，表明采用可實現的k-ε湍流模型、重疊網格技術以及球鉸連接方式建立的數值模型，可以較好地實現雙車廂兩棲車的水動力性能預報。

2)低航速下前車體埋首而后車體仰首，高航速下前車體仰首而后車體埋首，原因主要是高航速下傾斜的防浪板提供了較大升力。總體上可以看出，雙車廂兩棲車的縱搖角度保持在1°以內，車體縱搖性能優良。

3)在靜水直航工況中，前后車體的縱搖結果表明兩車廂在球鉸連接的情況下通常保持中垂或中拱狀態，因此導致球鉸在z軸方向對前后車體的作用力最大，球鉸和對應的連接桿件設計需重點考慮z軸方向的作用力問題。

4 展望

水陸兩棲車在水中速度一般可達到12～13 km/h[1]，兩棲車目前存在的一個較大問題就是如何提高水中航速，解決該問題可以通過改進水下推進裝置增加推力、增加車輪收放裝置以及優化車體尤其是車頭的型線設計以降低車身阻力等方法實現；另一個問題是如何改善水動力性能，主要是減小縱傾和垂蕩運動，改善措施主要包括優化防浪板形狀與安裝角度、增加減搖裝置或者優化車身設計等。

對于排水量較大的雙車廂兩棲車，這類問題同樣亟待解決，未來的工作將主要采用CFD數值模擬方法實現兩棲車的優化設計，并結合少量模型試驗來改善其水動力性能。此外，目前對于兩棲車回轉性能和耐波性能的研究較少，這也是未來工作的重點。