大擺角單擺“周期”變化的解析解及其實驗應用
柴聰聰,鳳飛龍,王公正,衛芬芬
(陜西師范大學 a.物理學與信息技術學院,陜西 西安 710119; b.基礎實驗教學中心,陜西 西安 710062)
對于單擺的大擺角非線性振動,已有許多文獻進行了研究,但是許多模型忽略了空氣阻尼的作用,并不能解釋單擺周期測量中擺動“周期”隨擺次的變化[1-3];文獻 [4-6]研究了空氣阻尼作用下的非線性運動方程,但只考慮了擺角對于準周期的影響,未對擺動“周期”隨擺動次數的變化做進一步的研究;文獻[7]采用實驗數據擬合的辦法對這種“周期”-擺次關系給出了經驗公式,但只適用于特定擺長. 由于大學物理實驗教學中大擺角單擺實驗[8]擺長不定,理論上忽略空氣阻尼造成實驗系統誤差,而測量時采用累計測量求平均周期的方法不僅僅會減小隨機誤差而且會影響系統誤差,因此有必要對“周期”-擺次關系進行進一步的研究以期改進實驗教學.
本文首先在弱阻尼大擺角單擺運動方程的基礎上推導累計“周期”隨擺動次數變化的關系式,分析“周期”的變化規律. 然后利用已有實驗數據驗證公式的準確性以及利用它進行實驗系統誤差修正的設想.
1 弱阻尼大擺角單擺運動方程與“周期”解
對于擺長為l、擺角為θ的單擺,在空氣阻尼系數為c的條件下,根據角動量守恒得
(1)
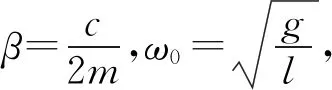
(2)
將sinθ泰勒展開,忽略高次項,取
(3)
得
(4)
根據文獻[5]可得該方程的解為
(5)


2βT′(n)+γe-2βT′(n)=p.
(6)
解之可得
(7)
式中W即朗伯W函數又稱為“歐米加函數”或“乘積對數函數”,在Matlab和Mathematica軟件中均有對應函數可以直接求解.


隨著βt增大,但增大不多時,e-2β t取二階近似e-2β t≈1-2βt+2β2t2,沿用以上計算過程可得θ=θ0e-β tcos {[1-γ(1-βt)]ωrt+φ0}. 解[1-γ(1-βT2′)]ωrT2′=2nπ并取正實根可得
(8)

2 “周期”解的實驗驗證與應用
基于文獻[7]中已知的實驗數據,首先對以上公式進行實驗驗證. 取擺長l=75 cm,g=9.794 07 m/s,β=0.005[5],不同擺角下第1個周期的實測與理論結果對比如表1所示.
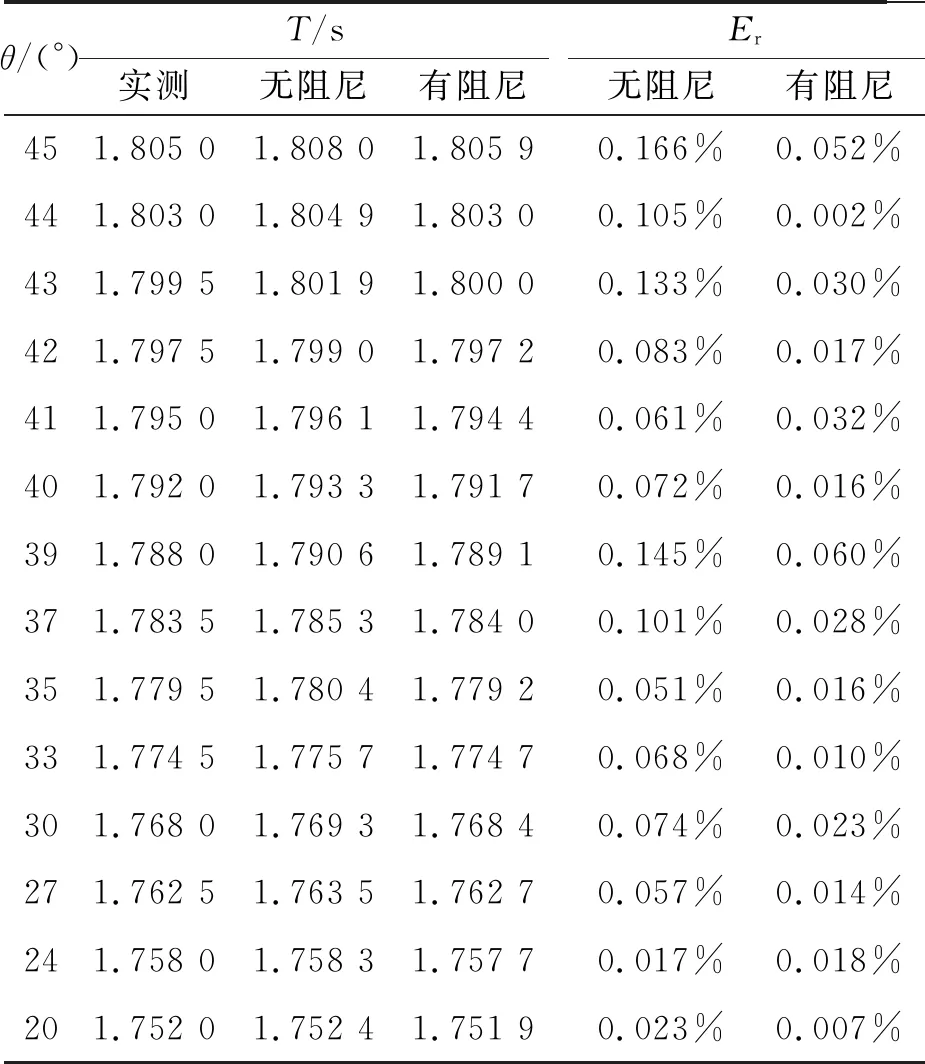
表1 不同初始擺角下單擺第1個周期的測量值
表1中無阻尼振動的周期由
(9)
計算. 由表1可見,考慮阻尼由式(7)計算所得結果比無阻尼情況下按式(12)計算所得結果偏差小了將近1個數量級(偏差平方和分別為0.001 2%,0.000 1%). 由此一方面可以驗證式(8)結果的準確性;另一方面也說明即使只測量1個周期,大擺角下無阻尼公式也存在較大系統誤差.
此外,根據文獻[7],如果采用累計測量求平均的方法測量周期,則結果如圖1所示,顯然隨著累計次數增加,實驗系統誤差更加明顯.
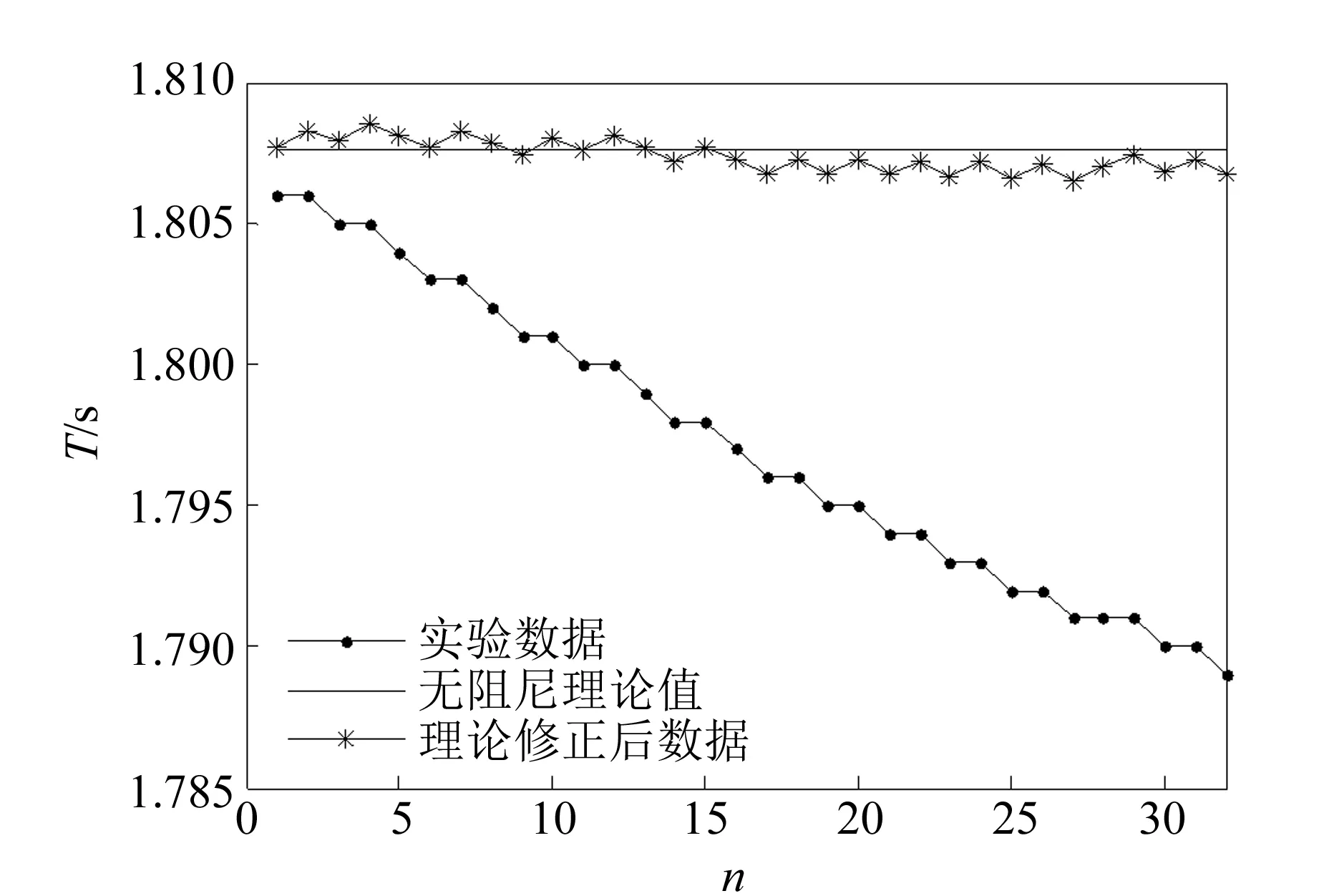
圖1 累計不同擺次時的平均周期
參照式(7)和式(12)引入系統誤差計算公式
ΔT=T-T′(n)/n,
(10)
并利用式(13)對實驗結果進行修正,如圖1所示,實驗結果可以更好地吻合理論設定而基本上不受累計次數的影響. 然而,由于文獻[7]中“累計”周期實際上是將每個周期測量結果累加后求平均得到的,所以隨著累計次數的增加,圖1中隨機誤差并無明顯變化,沒有體現累計測量提高修正數據精度的作用. 但如果實驗中直接對多個周期累計計時求平均,則周期測量的隨機誤差會進一步減小. 這種結合系統誤差修正和累計周期測量的方法可以減小實驗誤差,尤其是在用秒表計時,隨機測量誤差較大的實驗中.

