基于RSSI信號特征的室內分區指紋定位算法

高思遠，馮秀芳

(太原理工大學 信息與計算機學院，山西 晉中 030600)

0 引 言

常用的基于WiFi的室內定位技術主要有傳播模型法和基于WiFi的RSSI(received signal strength indicator)位置指紋法。基于RSSI的位置指紋定位方法在實際環境中有更好的定位效果，且易于部署，因此受到更多學者的青睞，國內外學者相繼提出了許多基于WiFi的RSSI位置指紋定位方法。Li Changgeng等將曼哈頓距離引入到WKNN算法中，并根據RSSI值各維的差異是否小于某一特定常數，增大或減小每個維度的RSSI差異[3]，該方法在一定程度上提高了算法與實際物理環境的相似性。XueWeixing等提出了一種利用最大RSSI觀測值的平均值來改進RSSI觀測值的算法，通過平滑度指數來評價RSSI信號的質量，從而選擇合適的RSSI觀測值[4]。李華亮等提出了一種基于核函數特征提取的室內定位算法，通過使用核函數特征提取方法訓練原始位置指紋，并有效地利用各個接入節點的接收信號強度信息，減少了RSSI信號采集次數和AP個數，降低了平均定位誤差[11]。

本文在現有研究的基礎上，從離線指紋庫構建、子區域劃分以及在線位置估計等方面提出了改進的基于RSSI的位置指紋定位方法。

1 基于WiFi的RSSI位置指紋定位算法

基于WiFi的RSSI位置指紋定位算法主要分為兩個階段，離線階段以及在線階段[15]。

1.1 離線階段

構建離線指紋數據庫。在待定位區域根據室內環境分布情況，均勻的選取a個參考點RP，標記為RP1、RP2、RP3、…、RPa；b個WiFi信號可接收點AP，標記為AP1、AP2、AP3、…、APb[15]。 在第i個參考點RPi處采集到來自第j個APj的RSSI值標記為：RSSIij=(RSSIi1,RSSIi2,…,RSSIij,…,RSSIib)， 將該參考點所在的區域、物理位置及其RSSI值共同構成一個位置指紋，所有參考點的位置指紋構成離線指紋數據庫見表1[15]。

表1 離線指紋庫

1.2 在線階段

在位置指紋定位研究領域中，關于RSSI向量匹配算法的研究成果比較豐富，諸如歐氏距離、概率分布、神經網絡、支持向量機、稀疏表示等等[14]。本文采用的匹配算法為歐氏距離法。傳統的WKNN算法通常使用歐氏距離進行相似度度量。在線階段，通過歐式距離(如式(1)所示)計算得出待定位點與離線指紋數據庫中所有參考點指紋的歐氏距離

(1)

然后使用KNN算法選擇指紋庫中與待定位點的歐氏距離最小的K個參考點的物理位置，利用式(2)進行位置估計

(2)

2 基于RSSI信號特征的分區指紋定位算法

基于WiFi的RSSI位置指紋定位算法在取得較高定位精度的同時也存在一定的缺陷。首先，不同類型的AP發射功率不同，在同一位置處的RSSI值存在差異性；同時，在線定位過程中通常使用KNN算法進行位置估計，需要對指紋庫中的所有數據進行搜索，計算量較大，搜索效率較低；其次，在定位過程中極易使用兩個歐式距離較小而物理距離較大的點進行位置估計從而增大定位誤差。為減少以上現象對定位精度的影響，提出基于RSSI信號衰減率(RSSIRATE-SVM)的分區聚類指紋定位算法。算法的主要流程為，首先在離線階段對待定位區域進行子區域劃分，然后使用各參考點處的RSSI信號變化率構建離線指紋數據庫；在線定位階段中，使用SVM算法對待定位點進行區域劃分，再使用二級指紋定位算法進行精確定位。

2.1 離線階段

2.1.1 子區域劃分

傳統的位置指紋定位算法中在線定位階段使用KNN算法進行位置估計，需將待定位點處的信號指紋與指紋庫中的所有指紋進行對比，根據其差異性進行位置估計。由于人為對待定位區域進行劃分時忽略了RSSI信號的分布特性，因此為了提高搜索效率，減少隨機性因素的干擾以及減少樣本搜索數量，本文依據RSSI信號分布特性提出了基于RSSI信號衰減率的子區域劃分法[15]。

(1)粗略劃分

由于RSSI信號容易受多徑傳播以及室內環境的影響而不穩定，通常使用對數路徑模型來描述其在室內環境中的傳播，如式(3)所示[15]。其中RSSI(d0) 表示距離信號發射點d0m處(通常為1 m)的信號強度值；n表示路徑損耗系數，受周圍環境影響，Xσ表示無線信號發送節點到接收節點之間的遮蔽影響因子，它受室內環境所影響，是標準差為σ的高斯分布隨機變量，d表示待定位節點與信號發射節點間的距離[15]

(3)

根據式(3)可得，RSSI信號與信號發射裝置間的距離存在一定的映射關系。研究表明，來自同一AP的RSSI均值在不同物理位置處的表現力不同，盡管RSSI值存在波動，但整體趨勢是越靠近AP的位置接收到的RSSI值越強。我們使用RSSI信號衰減率描述RSSI信號隨距離的變化情況，根據式(3)可構建RSSI信號衰減率模型，如式(4)所示[15]

rate(d)=-10nd0·(d·ln10)-1

(4)

圖1描述了隨著距離的變化RSSI信號的變化率情況。根據RSSI信號隨著距離變化的分布情況可以看出，隨著距離的不斷增大RSSI信號強度值逐漸減小，其信號變化幅度逐漸減弱；由RSSI信號變化率分布圖可以看出存在一個點p，p點處與信號發射點AP的距離為rm,在該點處RSSI信號變化率發生明顯變化，我們稱點p為最優衰減率特征點[15]。

根據圖1可以看出，當與AP的物理距離d≥r時，RSSI信號變化率逐漸趨于平緩，信號變化幅度不明顯，對RSSI信號空間距離度量的貢獻度較小。因此以最優衰減率特征點p處對應的距離r為半徑進行區域劃分以實現最優分區，使得RSSI特征較相似、RSSI信號變化明顯的參考節點更為集中。

圖1 RSSI信號衰減率變化

以各AP為中心，特征點p處對應的距離r為半徑進行粗略區域劃分，將室內定位區域劃分為l個圓形分類區areal,l∈[1,n]， 如圖2所示[15]。

圖2 區域劃分

(2)精確劃分

由于粗略劃分階段，采用圓形分類區進行子區域劃分，因此存在部分參考點未被劃分進任一子區域，稱這部分參考點為孤點；精確劃分階段，采用SVM算法對孤點進行精確分類[15]。

將已分類的參考節點作為訓練集對SVM進行多分類訓練，得出最優分類模型，訓練樣本集為 {(xi,ci)},i∈[1,n]， 若xi屬于areal，則標記c=1否則標記c=0， 超平面方程為[15]

f(x)=?·φ(x)+b

(5)

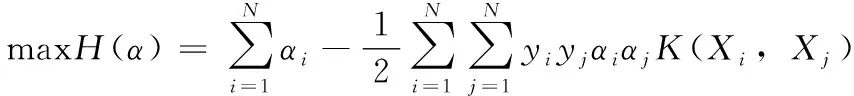
(6)

2.1.2 離線指紋庫建立

傳統的位置指紋定位算法中使用各參考節點處的RSSI值建立信號指紋數據庫，然而復雜的室內環境使得RSSI信號極易受到干擾，在線更新指紋數據庫需要耗費大量的人力物力；同時不同型號的AP其信號穩定程度及發射功率不同，很容易影響定位精度。因此本文提出使用各參考點處的RSSI信號變化率構建離線指紋數據庫。

由式(4)可以看出，信號衰減率與環境影響因子Xσ無關，因此，使用各參考點處的信號衰減率構建離線指紋數據庫可以忽略環境影響因子Xσ對定位結果的影響。

在各參考節點處采集來自各AP的RSSI信號值，通過式(4)計算RSSI信號衰減率。參考點RPm處的信號衰減率指紋為ratem=(rate1,rate2,…，raten)， 所有參考點處的信號衰減率及其物理位置構成離線指紋數據庫，見表2[15]。

表2 RSSI-RATE指紋庫

2.2 定位階段

在線定位階段首先使用SVM算法確定待定位點所屬子區域，其次使用二級指紋定位算法對待定位點進行位置估計。

2.2.1 RSSID指紋

在線定位階段引入SSD(single strength difference，SSD)的思想。即利用同一物理位置處，各分量RSSI之間的信號強度差構建RSSID信號序列。

根據式(3)有

(7)

(8)

由式(7)、式(8)可得

(9)

根據式(9)可得ΔRSSI與Xσ無關。即Xσ的變化不會對同一位置處不同AP的信號強度差值ΔRSSI產生影響，可提高RSSID指紋的穩定性。RSSID指紋構造公式如下

RSSIDi,j=RSSIi,j-RSSIi,j+1,j∈[1,n-1]
RSSIDi=(RSSIDi1,RSSIDi2,…,RSSIDi,n-1)

(10)

2.2.2 二級指紋精確定位

在待定位點所屬區域中首先使用KNN算法計算出離線指紋庫中與待定位點的RSSI信號變化率指紋距離最小的ak個參考點集RPa

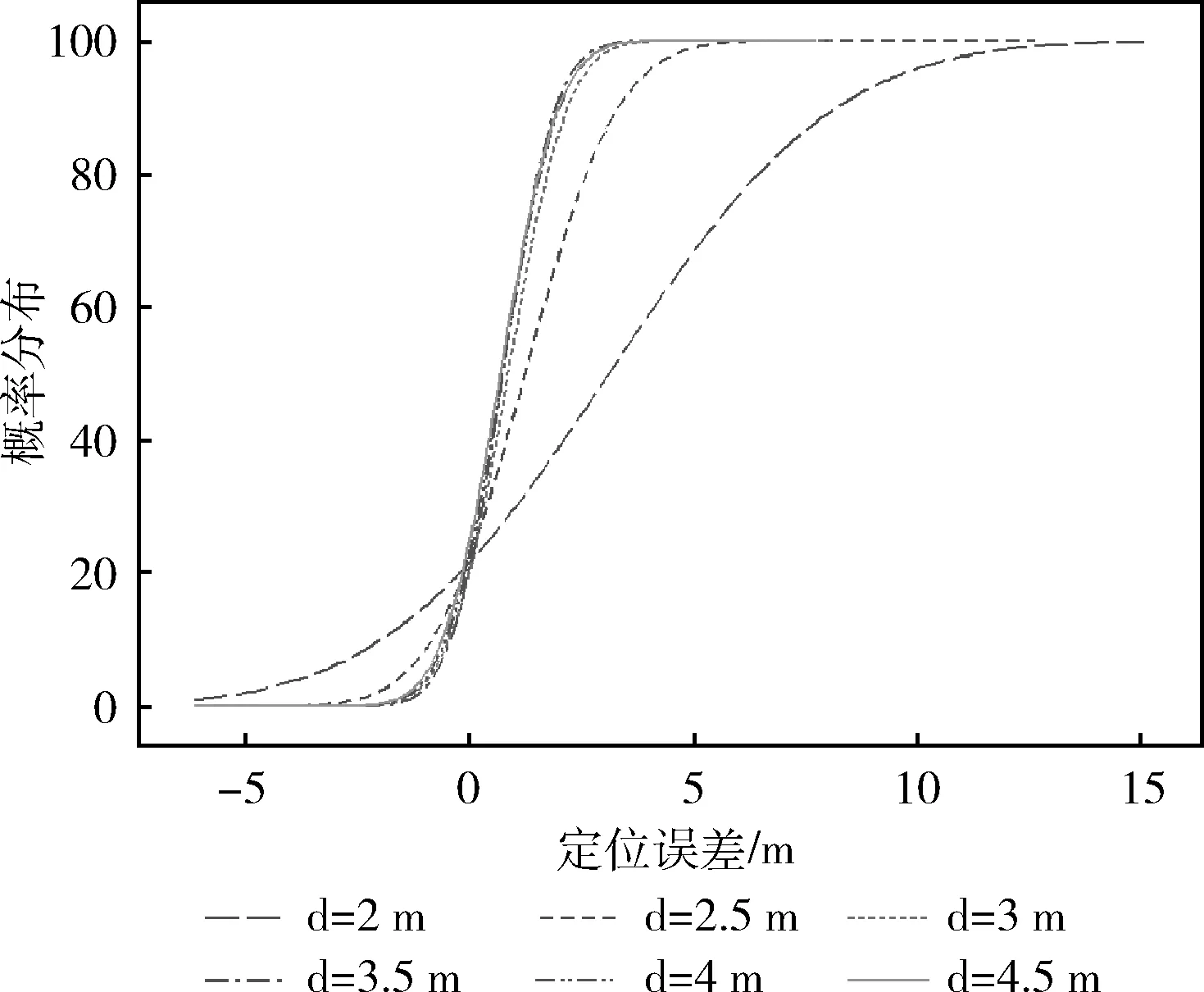
RPa={RPa1,RPa2,…,RPak}
RPa?RP,1≤ak

(11)

其次，使用KNN算法求出與待定位點的RSSID指紋距離最小的前bk個參考點集RPb

RPb={RPb1,RPb2,…,RPbk}
RPb?RP,1≤k≤m

(12)

根據參考點集RPa、RPb求出最相似參考點集RPsim=RPa∩RPb， 最后使用KNN算法利用最相似參考點集對待定位點進行位置估計。

本文所提算法流程如圖3所示。

圖3 算法流程

3 實驗結果與分析

為驗證本文所提算法的有效性，使用MATLAB R2014b進行仿真實驗與分析。本次實驗在一面積為11 m×7 m的實驗場地進行，在室內布置3個信號發射裝置，物理位置分別為 (2.5,3),(6,5),(9.5,2.5)。 在房間內部以 1 m 為間隔設置60個參考節點，在房間邊緣處以0.5 m為間隔設置72個參考點。離線階段在參考點處采集RSSI信號序列建立離線指紋庫，隨機生成20個待定位點的指紋數據作為測試數據。將本文所提算法與基于KNN算法、WKNN算法以及貝葉斯算法的定位效果進行對比，實驗結果如下所示。

3.1 r的選取

通過實驗對子區域劃分半徑r的選取進行了分析。實驗測定了當子區域劃分半徑分別為2 m、2.5 m、3 m、3.5 m、4 m以及4.5 m時，使用KNN算法對待測點進行位置估計時的定位誤差，實驗結果見表3[15]。

表3 子區域劃分半徑及定位誤差

表3從定位誤差以及計算量等方面對子區域劃分半徑的定位效果進行了分析。根據表3可以看出，以2 m為子區域劃分半徑時平均定位誤差為3.13 m，以2.5 m為子區域劃分半徑時其平均定位誤差為1.26 m，相比劃分半徑為2 m時的定位誤差下降了約60%，數據計算量是初始計算量的1.73倍；以3 m為子區域劃分半徑時其平均定位誤差為0.88 m，相比以2.5 m為半徑進行子區域劃分時定位誤差下降了約21%，數據計算量是初始計算量的2.5倍；以3.5 m為子區域劃分半徑時，其平均定位誤差為0.77 m，數據計算量是初始計算量的3.13倍；以4 m為半徑進行子區域劃分時，平均定位誤差為0.75 m，數據計算量是初始計算量的4.18倍；以4.5 m為半徑進行子區域劃分時，平均定位誤差為0.71 m，數據計算量是初始計算量的4.78倍[15]。

圖4描述了以不同半徑進行子區域劃分時的定位誤差，可以看出當子區域劃分半徑小于3 m時，定位誤差較大且變化較為明顯；當子區域劃分半徑大于3 m時，定位誤差較小且變化逐漸趨于平穩。根據實驗結果，選擇以3 m為半徑進行子區域劃分，可在計算量較小的情況下取得較高的定位精度[15]。

圖4 子區域劃分半徑及其誤差分布

圖5描述了以不同半徑進行子區域劃分時的誤差累計分布圖。根據圖5可以看出子區域劃分半徑大于3 m時的定位效果明顯優于子區域劃分半徑小于3 m時的情況[15]。

圖5 以不同半徑進行子區域劃分的誤差累計分布

3.2 RSSIRATE-SVM算法性能驗證

圖6為使用本文所提算法RSSIRATE-SVM與使用RSSI信號指紋結合KNN、WKNN、Bayes算法的定位誤差分布圖。根據圖6可以看出，本文所提RSSIRATE-SVM算法定位誤差與其它3種算法相比誤差較小。

圖6 RSSIRATE-SVM、KNN、WKNN、Bayes算法定位誤差分布

表4從最大誤差、最小誤差以及平均誤差等方面對RSSIRATE-SVM、KNN、WKNN、Bayes算法的定位效果進行了對比。結合表4可得，KNN算法的平均定位誤差為1.85 m，WKNN算法的平均定位誤差為1.64 m，Bayes算法的平均定位誤差為1.37 m，RSSIRATE-SVM算法的平均定位誤差為0.91 m。由此可得，本文提出的基于RSSI信號變化率的區域劃分算法及二級指紋定位算法可以有效降低定位誤差，提高定位匹配度。

表4 RSSIRATE-SVM、KNN、WKNN、Bayes定位誤差對比

4 結束語

本文提出的基于RSSI信號衰減率的分區聚類室內指紋定位算法，通過使用RSSI信號衰減率選擇最優區域劃分半徑，降低了定位過程中出現兩個點RSSI指紋歐式距離較小而物理距離較大的情況對定位精度的影響；同時區別于傳統的使用RSSI信號值建立離線指紋庫的方法，提出使用不同參考點處的RSSI信號衰減率建立離線指紋庫，降低了定位過程中由于環境變化干擾RSSI信號而引起的誤差。下一步將對離線指紋數據庫的實時更新進行深入研究。